在大地电磁二维Occam反演中求取拉格朗日乘子方法改进

朴英哲，李桐林，刘永亮

1.金策工业综合大学资源探测工学系，朝鲜 平壤 999093

2.吉林大学地球探测科学与技术学院，长春 130026

0 引言

大地电磁反演的非唯一性是众所周知的［1－3］，而Occam反演是克服该缺陷的方法之一。在大地电磁（magnetotellurics，MT）数据解释中，Constable等［2］初次将Occam反演这种说法用于一维反演。Occam反演是光滑模型反演，具有较好的稳定收敛性和结果可靠性。另外，Occam反演能够引入先验信息来去掉对已知构造边界处的光滑度或者加上对同类电性单元的电阻率差的限制。基于这些优点，Occam反演广泛应用于 MT二维解释［3－4］。

Siripunvaraporn 等［5－7］研 究 出 了 数 据 空 间Occam反演方法，并且成功地应用于MT二维、三维反演。他们在数据空间方法中，又结合了CG的优点而研究出了 DCGOCC［8］。张罗磊等［9］还提出了光滑模型与尖锐边界相结合的反演方法。对Occam反演普遍而详细的论述可见于文献［2－3，5－7］中。

Occam反演不但被应用于MT数据解释而且被应用于多种地球物理勘探反演解释当中［10－17］。MT二维数据Occam反演方法［3］是其中最有代表性的例子。拉格朗日乘子是介于模型光滑和数据拟合间的折衷参数，每次迭代反演为了求取适当的拉格朗日乘子需要进行多次正演计算，尤其在接近收敛时更是如此。为此，不少研究人员提出了直接求取拉格朗日乘子的方法。

吴小平等［18］提出了每次迭代以固定的比率减少拉格朗日乘子的方法，还指出虽然这种反演的结果非最光滑模型，但因为观测数据是反演解释的第一手资料，而模型光滑作为反演约束条件仅是稳定迭代的手段，只有使理论数据与实际数据尽可能一致才能分辨所有的构造特征，尤其对精确数据的反演更是如此。但这种方法忽视了因观测数据存在噪声而产生多余构造的可能性，以及对精确数据来说，调整正演与观测数据之间的拟合差期望值是更合理的。吴小平的求取方法速度快，在3DMT正演需要较长时间的情况下，反演多采取了该方法［8，19］。MT三维反演的拉格朗日乘子选取方法与吴小平等的方法有一些差别之处，就是随着拟合差的变化而减小或增大拉格朗日乘子。

张罗磊等［9］提出的方法是根据反演目标泛函中数据误差部分和模型粗糙度部分占用的比重选取初始值，每次迭代随模型粗糙度的变化，在总体粗糙度没有减少时，以粗糙度变化率来减少乘子。这种方法也快，但容易陷入局部极小值。

另外，关于与拉格朗日乘子类似的Tikhonov正规化因子的选取方法有几种，如基于离差原理（discrepancy principle）的 方 法［20］、广 义 交 叉 验 证（generalized cross validation）方 法［21］、L－曲 线（L－curve）法［22］和 U－曲线（U－curve）法［23］。这些方法从每次迭代需要反复计算正演的这一点上来看与deGroot－Hedlin等［3］的 Occam2DMT 相似（以下将deGroot－Hedlin等［3］的方法称为 Occam2DMT）。

笔者首先介绍了Occam反演和Occam2DMT的拉格朗日乘子求取方法，然后提出了改进的方法。接着通过几种模型实验证明了改进的方法比原方法更有效，比吴小平等［18］的方法更稳定。

1 Occam反演中拉格朗日求取方法改进

1.1 Occam反演方法及拉格朗日乘子求取方法

Occam反演是在一定的拟合误差标准下求使模型粗糙度最小的解。因此，反演的目标泛函以模型粗糙度、拟合差及拉格朗日乘子构成：

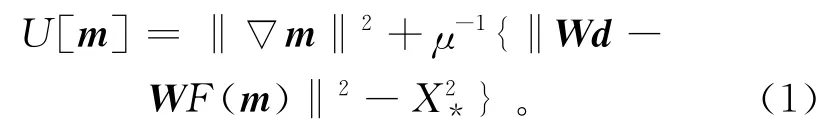
其中：m为模型向量；‖▽m‖2为模型粗糙度；d为观测数据向量；F为正演算子；W为利用数据标准差进行规一化的矩阵；‖Wd－WF（m）‖为数据拟合差（以下用X表示）；X＊为拟合差的期望值；μ为拉格朗日乘子。

这里模型向量的泛函是非线性，为此，在初始模型m1附近作线性化，用迭代方法求解。第二次迭代模型近似为

由式（2）可知，m2为μ的函数，数据拟合差也是μ的函数。从m1得到m2时，随μ值从0到无穷大变化，模型m2沿模型空间中的一定轨道移动。模型空间中的每个模型都对应相应的拟合差，所以可以想到模型空间中的拟合差等值线（图1）。

Occam2DMT首先用Brent方法［24］找到一个μ2，使得数据拟合差极小，即

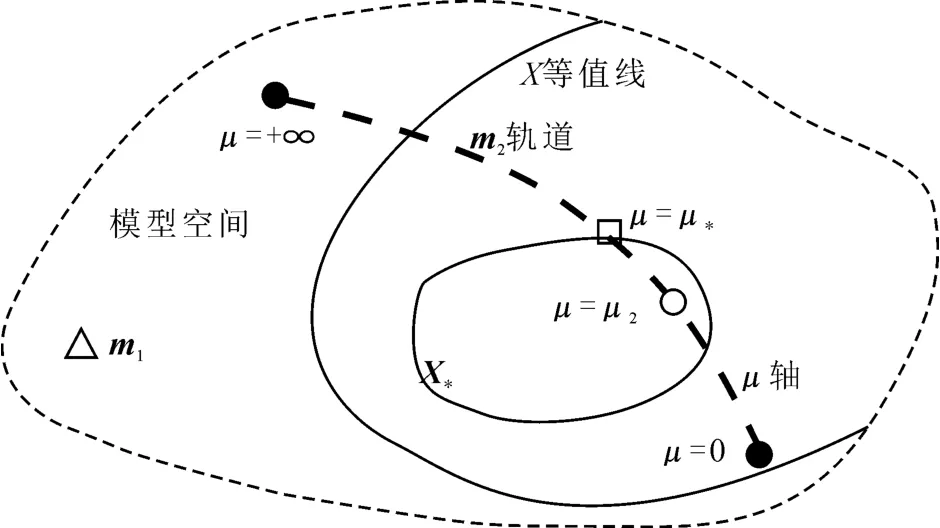
图1 μ值和拟合差的关系Fig.1 Relationship betweenμand root mean square misfit

Brent方法［24］需要事先确定包含极小值的区间（a，b），为此，在初始μ0附近找到a、b及μ1（μ1∈（a，b）），令

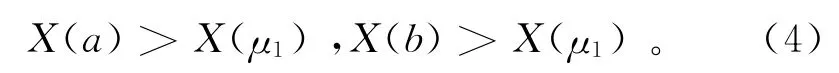
若X（μ1）或X（μ2）小于误差限，利用 van Wijngaarden－Dekker－Brent方法［24］搜索m2轨道与误差限等值线交叉的最大的μ值，令μ＊为此值，即

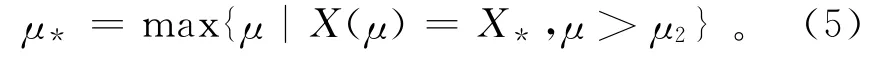
若X（μ2）＞X＊，令μ＊＝μ2。

此μ＊值是最佳拉格朗日乘子。按上述原理，Occam2DMT求取μ＊的方法由以下3个步骤组成。

①确定极小值区间：找到满足式（4）的a、b及μ1。若X（μ1）≥X＊，转移到步骤②；否则转移到步骤③。

②X极小化：在区间（a，b）中，用Brent方法搜索满足式（3）的极小点μ2。若X（μ2）＜X＊，转移到步骤③；否则令μ＊＝μ2，终止。

③交叉点搜索：用WDB方法搜索满足式（5）的μ＊。

经以上3个步骤确定μ＊之后，将此值代入式（2）计算m2。以上3个步骤需要进行反复正演，正演次数直接关系到反演的计算量。

1.2 改进的拉格朗日乘子求取方法

一般来说，Occam反演由2个阶段组成：第一阶段是使拟合差减小到拟合差期望值，第二阶段是在保持拟合差为期望值的同时，搜索粗糙度最小的模型。Occam2DMT在这2个阶段中，都利用上述的由3个步骤组成的方法求取μ＊。

在第一阶段的每次迭代中，除了最后迭代，拟合差都未达到期望值，所以在模型空间中m2轨道未交叉X＊等值线，未经过步骤③，搜索μ2达到目的。但在第一阶段的最后迭代和第二阶段的每次迭代中，都经过步骤③，因此目的是搜索μ＊的。那么此时能够使求取μ＊的方法优化。

实际上，步骤①的目的只是求函数X（μ）的极小值点；若在步骤①的反复计算中，有一点的X函数值小于误差限时（图2a），尽管未确定极小值区间，也可以直接转移到步骤③搜索大于μ1的交叉点μ＊。如此，可以排除不必要的计算，且结果μ＊值不受任何影响。

图2 求取拉格朗日乘子Fig.2 Choosing Lagrange multiplier

在第二阶段中，虽然模型m1的相应拟合差小于误差限，但也有步骤①a、b及μ1的相应拟合差都大于误差限（图2b），此时得进行步骤②。不过步骤②不必找到极小点，只需要有一个点函数值小于X＊。因此，在步骤②的反复计算中一旦有一点的X函数值小于误差限，就可以终止X函数极小化，开始搜索交叉点。如此未影响μ＊值，也排除多余的计算。

很明显，上述改进更符合于Occam思想，并且其求解空间与原方法一致。

下一个问题是如何设定每次迭代的初始μ0。也许μ0越接近最佳值μ＊，计算量越少。第一迭代的初 始 值由使用者预定。第一迭代以后，Occam2DMT令μ0为前次迭代的μ2。在反演的第一阶段中μ2与μ＊一致，为此这种选择是适当的。但在反演第二阶段中μ2与μ＊稍微差别，所以这种选择可能不恰当。

根据模型实例，在模型光滑阶段中μ＊值的变化较小。因此令初始μ0为前次迭代的μ＊也许更合理。笔者考虑到试算模型的μ＊值变化特征，将模型光滑阶段中第i次迭代的初始值设定为，其 中为前两次迭代的μ＊值。若i＜3，令

经计算，本文方法与Occam2DMT求取的μ＊的误差很小（小于10－5），而且能够排除多余的正演计算。本方法的算法如图3。

图3 本文方法第i次迭代的算法Fig.3 Flow chart of the ith iteration of this inversion

2 模型实验与结果分析

为了比较本文方法和原方法以及吴小平等［18］的方法，构建了如图4所示的8种地电模型。模型1和模型2是电阻率100Ω·m均匀半空间中存在矩形异常体。模型1异常体的电阻率为1 000Ω·m，顶面埋深为7km；模型2异常体的电阻率为10、1 000Ω·m，顶面埋深为10km。模型3是电阻率为100Ω·m的围岩中存在电阻率10Ω·m传导性侵入 岩（deGroot－Hedlin 等［3］）。 模 型 4 和 5 与deGroot－Hedlin等［4］反演的模型相同。模型6是与Siripunvaraporn等［7］相似的邻近的不同电阻率块体模型（围岩电阻率为100Ω·m，异常体电阻率分别为10、1 000Ω·m）。对于所有模型利用趋肤深度来进行网格剖分和划分网格边界［25］。大地电磁场受地形影响［26］，笔者将模型7和模型8设定为起伏地形模型。对于起伏地形模型，为了保证正演精度，斜坡附近采用更周密网格。在起伏地形的坡角处，不同研究人员的辅助场计算方法不同［27］；为此，在坡角处未安置测点。测量数据为TE、TM 2种极化模式下的视电阻率和阻抗相位（模型1：6个测点、6个频点（0.486～0.002Hz的对数间隔）；模型2—模型6：11个测点、16个频点（1～0.001Hz的对数间隔），模型7、模型8：11个测点、16个频点（100～0.1Hz的对数间隔）），并在数据中加入了2%的随机噪声。反演初始模型为1Ω·m的均匀半空间，μ0值为5，X＊为1.1。

首先，原方法和本文方法比起来，每次反演迭代的μ＊值变化完全一致，当然反演结果也一致，只是在正演次数上有差别。表1为8个模型的原方法与调整μ0前和调整μ0后改进方法的正演次数比较。

表1 正演次数比较Table 1 Comparison of forward modeling number

可以看到所有模型正演次数均减少了20%～50%。调整μ0后正演次数小于调整前（除模型1），不过其效果并不大。

其次，比较本文方法（调整μ0后）和吴小平等的方法。吴小平等［18］方法的关键是如何选取减小拉格朗日乘子的比率λ及其下限μmin，通常取决于经验。本文确定Occam2DMT反演迭代的μ＊值是最佳选择，使比率和下限符合μ＊值的变化。

图4 地电模型Fig.4 Synthetic models

模型1—4中μ＊的变化和模型5—8中μ＊的变化稍有差别（图5）。因此，把8种模型分成2组。对第一组（模型1—4，图5a），令

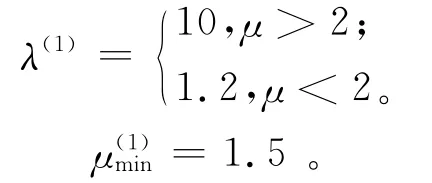
对于第一组模型，吴小平等［18］的方法比本文方法收敛快，反演结果虽非最光滑模型，但其粗糙度和最光滑模型（Occam2DMT反演结果）的粗糙度差别很小。这种效果是由于适当选取了λ和μmin。

但是，用同样的参数反演第二组模型，结果分散。因此，对第二组（模型5—8，图5b），令

2个方法的迭代次数不相等，所以用反演所需总的时间来对比2种方法（图6）。

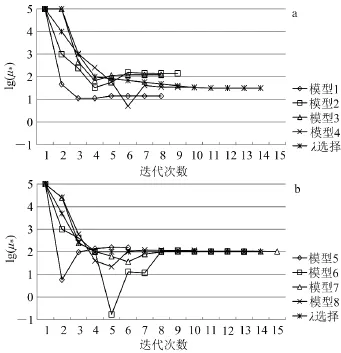
图5 μ＊随迭代次数的变化及λ选择Fig.5 Variation ofμ＊along iteration number and choosingλ

图6 第二组模型数据拟合差变化比较Fig.6 Comparison of root mean square misfit variation for the second model group

对于所有的模型，本方法稳定收敛。相比之下，吴小平等的方法收敛速度慢。本方法大约100s时已收敛到误差限内，此后计算是找最光滑模型，但吴小平等［18］的方法大约250s时才收敛（图6a），甚至未收敛（图6b）。对于模型7和模型8，吴小平等方法虽收敛到误差限，但其收敛很不稳定且收敛时间比本方法更长（图6c，d）。

对于模型6的反演结果，本文方法和吴小平的方法都找到设计异常体，不过在吴小平的方法反演剖面中地表附近（水平距离13～15km）出现了电阻率较低的异常体（图7）。这是因为模型6的反演没收敛，同时也说明了最光滑模型和非最光滑模型的区别。

图7 模型6反演结果对比Fig.7 Comparison of model 6inversion results

对不同的几组λ、μmin反复进行试算，对第二组模型吴小平等方法的结果也没有改善。其原因是每次迭代都要减小拉格朗日乘子。其实从图5可以看出，适当的拉格朗日乘子并非是一律减小的。吴小平等指出该方法对其参数取值无太严格要求，但他的例子是一维的，且二维反演的非惟一性比一维反演严重。这也是吴小平等方法效果不好的原因。

3 野外数据反演结果

用本文方法处理了本溪—集安地区大地电磁第5线数据（图8）。使用的仪器是加拿大凤凰公司的V5－2000系列电磁仪。测线的方向大致从北西到南东。在测线上共有29个测点，测点间平均距离为大约5km。测量数据中采取了13个频点（360.0～0.7Hz的对数间隔）。根据采集物性样本的电阻率测量结果，该地区的地下电阻率范围为数百到数万Ω·m。考虑到地形起伏与趋肤深度，把剖面网格单元大小设定为宽250～750m，高100～2 000m。反演初始模型为1 000Ω·m的均匀介质，μ0值为5，X＊为3.5。

图8 5线的反演结果Fig.8 Inversion result of line 5

本文方法和Occam2DMT方法的反演总迭代都为8次，结果模型的粗糙度都为29.97。不过正演次数分别为52和78次，计算时间分别为26h20 min和35h30min，反演结果一致，如图8所示。

4 结论

虽然Occam2DMT具有收敛稳定性和结果可靠性的优点，但由于其利用了Press等的算法，在靠近解时正演次数增大，所以其计算时间较长。为了缩短反演时间，减少正演次数很重要。以固定的比率减小或增大拉格朗日乘子的方法，虽因在每次迭代中只需一次进行正演而很快，但在实际应用中，若使用者不进行人为调整反演参数，容易造成收敛失败或虚伪构造。笔者在求取拉格朗日乘子的一维搜索中排除多余的正演计算，使得Occam反演速度加快。本文通过对几种模型计算和野外数据反演，得出如下结论。

1）本文方法总能获得与Occam2DMT方法一致的解，在反演的拟合差下降到满足期待值阶段和光滑模型阶段，计算效率有明显提高。根据模型实验，可以减少正演次数20%～50%。

值得提出的是，当观测数据含有较强干扰噪声或地下电阻率较复杂时，无法求得在预定误差范围内的解，此时，本文方法不能有效地减少正演次数来减少计算时间。

2）本文方法的反演结果是粗糙度最低的模型。结果不但可靠，而且其收敛性也很稳定。

（References）：

［1］刘国栋，陈乐寿.大地电磁测深研究［M］.北京：地震出版社，1984.Liu Guodong，Chen Leshou.The Study of Magneto－telluric Sounding［M］.Beijing：Seismological Publishing House，1984.

［2］Constable S C，Parker R L，Constable C G.Occam’s Inversion：A Practical Algorithm for Generating Smooth Models from Electromagnetic Sounding Data［J］.Geophysics，1987，52（3）：289－300.

［3］deGroot－Hedlin C D，Constable S C.Occam’s Inversion to Generate Smooth Two Dimensional Models from Magnetotelluric Data［J］.Geophysics，1990，55（12）：1613－1624.

［4］deGroot－Hedlin C D，Constable S C.Inversion of Magnetotelluric Data for 2DStructure with Sharp Resistivity Contrasts［J］.Geophysics，2004，69（1）：78－86.

［5］Siripunvaraporn W，Egbert G.An Efficient Data－Subspace Inversion Method for 2DMagnetotelluric Data［J］.Geophysics，2000，65（3）：791－803.

［6］Siripunvaraporn W，Uyeshima M，Egbert G.Three－Dimensional Inversion for Network－Magnetotelluric Data［J］.Earth Planets Space，2004，56：893－902.

［7］Siripunvaraporn W，Egbert G，Lenbury Y，et al.Three－Dimensional Magnetotelluric Inversion：Data－Space Method［J］.Phys Earth Planet Inter，2005，150：3－14.

［8］Siripunvaraporn W，Sarakorn W.An Efficient Data Space Conjugate Gradient Occam’s Method for Three－Dimensional Magnetotelluric Inversion［J］.Geophys J Int，2011，186，567－579，doi：10.1111/j.1365－246X.2011.05079.x.

［9］张罗磊，于鹏，王家林，等.光滑模型与尖锐边界结合的MT二维反演方法［J］.地球物理学报，2009，52（6）：1625－1632.Zhang Luolei，Yu Peng，Wang Jialin，et al.Smoothest Model and Sharp Boundary Based Two－Dimen－sional Magnetotelluric Inversion［J］.Chinese Journal of Geophysics，2009，52（6）：1625－1632.

［10］刘羽，王家映，孟永良.基于PC机群的大地电磁Occam 反演并行计算研究［J］.石油物探，2006，45（3）：311－315.Liu Yu，Wang Jiaying，Meng Yongliang.PC Cluster Based Magnetotelluric 2－D Occam’s Inversion Parallel Calculation［J］.GPP，2006，45（3）：311－315.

［11］Parker R L.Geophysical Inverse Theory［M］.New Jersey：Princeton University Press，1994.

［12］deGroot－Hedlin C D.Inversion for Regional 2－D Resistivity Structure in the Presence of Galvanic Scatterers［J］.Geophys J Int，1995，122：877－888.

［13］LaBrecque D J，Ward S H.Two－Dimensional Cross－Borehole Resistivity Model Fitting［J］.Geotechnical and Environmental Geophysics，1990，1：51－57.

［14］Songkhun Boonchaisuk，Chatchai Vachiratienchai，Weerachai Siripunvaraporn.Two－Dimensional Direct Current（DC）Resistivity Inversion：Data Space Occam’s Approach［J］.Physics of the Earth and Planetary Interiors，2008，168：204－211.

［15］翁爱华.Occam反演及其在瞬变电磁测深中的应用［J］.地质与勘探，2007，42（5）：74－76.Weng Aihua.Occam’s Inversion and Its Application to Transient Electromagnetic Method［J］.Geology and Prospecting，2007，42（5）：74－76.

［16］Huang Z X，Su W，Peng Y J，et al.Rayleigh Wave Tomography of China and Adjacent Regions［J］.J Geophys Res，2003，108（B2）：ARTN 2073.

［17］Greenhalgh S A，Bing Z，Green A.Solutions，Algorithms and Inter－Relations for Local Minimization Search Geophysical Inversion［J］.J Geophys Eng，2006，3：101－113.

［18］吴小平，徐果明.大地电磁数据的Occam反演改进［J］.地球物理学报，1998，41（4）：547－554.Wu Xiaoping，Xu Guoming.Improvement of Occam’s Inversion for MT Data［J］.Chinese Journal of Geophysics，1998，41（4）：547－554.

［19］Newman G A，Alumbaugh D L.Three Dimensional Magnetotelluric Inversion Using Non－Linear Conjugate Gradients［J］.Geophys J Int，2000，140：410－424.

［20］Pereverzev S.Morozov’s Discrepancy Principle for Tikhonov Regularization of Severely Ill－Posed Problem in Finite－Dimensional Subspaces［J］.Numerical Functional Analysis and Optimization，2000，21（7）：901－916.

［21］Haber E，Oldeburg D.A GCF Based Method for Nonlinear Ill－Posed Problems［J］.Computational Geosciences，2000，4（1）：41－63.

［22］Hansen P C，Leary D P.The Use of the L－Curve in the Regularization of Discrete Ill－Posed Problems［J］.SIAM Journal on Scientific Computing，1993，14（6）：1487－1503.

［23］Stando D K，Rudnicki M.Regularization Parameter Selection in Discrete Ill－Posed Problems：The Use of the U－Curve［J］.International Journal of Applied Mathematics and Computer Science，2007，17（2）：157－164.

［24］Press H W，Teukolsky A S，Vetterling T W，et al.Numerical Recipes in Fortran 77［M］.New York：Cambridge University Press，1997.

［25］汤井田，薛帅.MT有限元模拟中截断边界的影响［J］.吉林大学学报：地球科学版，2013，43（1）：267－274.Tang Jingtian，Xue Shuai.Influence of Truncated Boundary in FEM Numerical Simulation of MT［J］.Journal of Jilin University：Earth Science Edition，2013，43（1）：267－274.

［26］赵广茂，李桐林，王大勇，等.基于二次场二维起伏地形MT有限元数值模拟［J］.吉林大学学报：地球科学版，2008，38（6）：1055－1059.Zhao Guangmao，Li Tonglin，Wang Dayong，et al.Secondary Field－Based Two－Dimensional Topographic Numerical Simulation in Magnetotellurics by Finite Element Method［J］.Journal of Jilin University：Earth Science Edition，2008，38（6）：1055－1059.

［27］Li Shenghui，Booker J R，Aprea C.Inversion of Magnetotelluric Data in the Presence of Strong Bathymetry/Topography［J］.Geophysical Prospecting，2008，56：259－268.