中国降水混沌识别及空间聚类

危润初，肖长来，张余庆，梁秀娟

1.吉林大学地下水资源与环境教育部重点实验室，长春 130021

2.南京信息工程大学遥感学院，南京 210044

0 引言

近年来，我国旱涝灾害的频次和受灾范围均呈扩大趋势，对降水系统的研究显得尤为重要。无论是在小的还是大的时间和空间尺度，降水事件都不是很稳定，表现出非随机却貌似随机的特征［1］，其动力系统过程复杂而连续。基于随机统计理论的传统研究是利用降水序列的随机性或统计特性来挖掘降水规律，但是这些理论不是基于降水过程的物理机理而建立的模型，因此很难揭示降水过程内在的系统动力结构［2］。以混沌理论为核心的当代非线性科学的迅猛发展有力地推动了水文时间序列分析的研究。水文系统是一个复杂的非线性系统，具有产生混沌的基本条件，即对初始条件的敏感性和内在的随机性，混沌方法已成为水文研究的重要工具［3－6］。传统的混沌识别方法主要是建立在相空间重构基础上的饱和关联维数法（G－P）、Lyapunov指数法和Kolmogorov熵等方法［7］，但是由于水文系统的特殊性，这些方法在运用过程中还存在一些问题。比如：重构相空间所需的延迟时间τ和嵌入维数D的确定存在一定的主观性与不确定性；不同方法计算得到的值往往差别较大［2］；此外由于我国大部分气象站都是建国后才设立，降水序列的长度一般有限，而传统的混沌研究方法一般对时间序列长度有严格要求［8］。

我国地域广阔，跨越了40个纬度、70个经度，地形复杂多变、海陆位置不一，而且受到多种大气环流的影响，因此降水系统具有明显的区间差异。多年来，很多学者就我国的降水分区做出了大量的研究［9－13］，这些研究成果一定程度上反映了降水的空间分布特征，但是对反映区域降水系统复杂性的空间分布尚显不足。混沌反映确定性系统内在的随机性，其度的大小表征混沌系统所具有的不规则程度和复杂程度［14］，因此可以通过对降水混沌度进行顾及混沌属性的空间聚类来研究降水动力系统的空间变异。

由于我国地面气象站监测的起始时间不一，在尽可能多地利用已有气象站资料外，还应尽量使时间序列样本更多。因此选用640个监测序列较全的气象台站（其中国家级636个，省级4个）1960—2011年的逐月降水数据，引入0－1混沌测试方法对各台站月降水序列进行混沌识别与计算，并运用基于密度的顾及非空间属性的空间聚类方法（DBSC）对640个台站的混沌计算结果进行空间聚类，用于分析我国降水序列的混沌空间变异规律。

1 0－1混沌测试

1.1 0－1方法介绍

0－1测试方法是 Georg A.Gottwald和Ian Melbourne提出的一种新的时间序列混沌特性识别方法［15－17］。该方法直接进行时间序列混沌特性的测试，根据计算的结果是否接近于1或0来判断序列的是否具有混沌特性。

假设时间序列为φ（j），其中j＝1，2，…，N，令c为区间（0，π）内的随机常数，则定义

定义函数pc（n）和qc（n）的均方位移Mc（n）为

pc和qc的散布特征可以通过对均方位移Mc（n）的分析来进行研究：如果时间序列是有序的，则Mc（n）是一个有界函数；如果时间序列具有混沌特性，则Mc（n）随时间线性增长。因此只要计算出Mc（n）对应于n的渐近增长率Kc，就可以来判断数据序列的混沌特性［3］。由于Mc（n）的收敛性不好，因此给出修正的均方位移M（n）：

M（n）与Mc（n）渐近增长特性相同，但其具有更好的收敛性［15］。由于降水序列长度是有限的，因此用降水序列的平均值来近似替代E（φ），即E（φ）＝对于n的取值范围，一般建议n≤N/10［15－18］。渐近增长率Kc的计算定义有2个：一是把Kc定义为lgM（n）与lgn的线性回归系数；二是把Kc定义为M（n）与n的相关系数，即

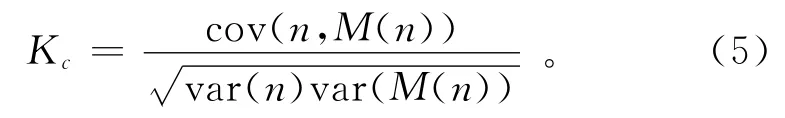
两种定义均反映M（n）与n的线性关系。在实际应用中，后者表现出更好的应用效果［12］，因此本次研究采用第2种定义进行计算。如果Kc接近1，表示该时间序列具有混沌的特性；如果Kc接近0，表示该时间序列不具有混沌特性。计算过程中，一般选取Nc个随机常数c，计算得到Nc个Kc。由于某些孤立的c存在共振离群的现象，这会对Kc的平均值产生较大影响，因此一般建议将Kc的中位数K做为最终值［12］。

目前该方法在多领域得到应用，其有效性得到了验证［16，18－22］，但是其应用范围还很有限，尤其是在混沌程度比较、混沌控制和预测方面还没有相关的研究成果。本次研究通过对全国640个气象台站的月降水序列进行混沌计算和比较发现，该方法能够反映数据序列的混沌度。

1.2 0－1混沌验证

为了验证0－1测试方法的混沌识别和比较的有效性，本次研究引入混沌研究的一个经典模型——Chebyshev映射。Chebyshev映射又叫Chebyshev迭代，按照如下方程进行反复迭代［23］：

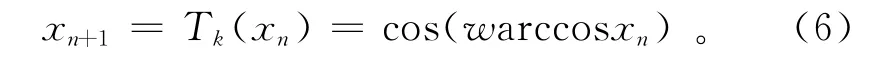
Chebyshev方程中变量x的值随参数w的变化由周期逐次加倍进入混沌状态，即由倍周期分岔通向混沌（图1a）。在w＝1.0附近，x的分布出现扰动，此后序列分岔进入半混沌状态；当w＞1.4时，序列进入混沌状态。传统上根据Lyapunov指数λ来判断系统的混沌特性。λ值能反映相轨迹有无扩散运动特征，其大小反映了系统的混沌程度［24］：当λ＜0时，系统有稳定的不动点；λ＝0时，对应着分岔点或系统的周期解；当λ＞0时，系统具有混沌特征［25］。由Chebyshev映射的λ－w关系图（图1b）可以发现：当w＜1.0时，系统动力学形态比较简单，处于稳定状态，λ值始终小于0；在w＝1.0附近，对应于x分布的扰动，λ值出现一个脉冲，此后系统进入半混沌状态，λ＞0。

通过计算得w从0.0逐渐增大的各序列的0－1混沌测试结果（图2）。测试结果表明，随着w的变化，系统从有序变为半混沌，最后进入完全混沌状态。K值初期趋近于0.0，在w＝1.0附近对应于系统扰动和λ值脉冲，K值也出现了局部震荡，随后快速增长；在w＞1.4后，K值趋近于1.0。

图1 Chebyshev映射Fig.1 Chebyshev Map

图2 K－w关系曲线Fig.2 Curve Kversus w

图3为w＝0.5（有序）、w＝1.2（半混沌）和w＝2.5（混沌）的 Chebyshev序列的p－q轨迹相图（c＝2.5）、不同c值条件下M（n）－t关系曲线图和Kc－c散点图。由图3可知：当w＝0.5，即系统为有序稳定时，p－q轨迹范围有界确定，均方位移M（n）随时间变化无增长趋势，其Kc的计算值稳定地分布在0.00附近；当w＝1.2时，系统为半混沌状态，p－q轨迹开始出现杂乱现象，部分M（n）－t曲线呈现线性增长特征，Kc的值也开始向1.00移动；当w＝2.5时，系统为混沌状态，p－q轨迹呈现出布朗运动的特性，M（n）随时间均呈现出明显的线性增长，Kc的值的分布趋近于1.0。

Chebyshev映射的0－1测试的结果与其倍周期分离图和最大Lyapunov指数图结论一致，这就验证了该方法的有效性；同时K随w的变化关系也说明，0－1方法能够反映系统不同程度的混沌特性。

2 基于密度的顾及非空间属性空间插值

DBSC算法［26－28］由我国学者邓敏和刘启亮等人提出，包括了2个步骤，即空间邻近域的构建和顾及非空间属性的空间聚类。

2.1 空间邻近域的构建

对于分布不规则的数据集，传统的Delaunay三角网建立的邻接关系在边缘处存在一定的误差［29］。DBSC算法采取整体－局部的层次边长约束策略对三角网的边长进行修剪，发展了整体与局部边长约束准则。

假定SDB是某空间数据库，DT（SDB）表示SDB的Delaunay三角网，其中每一个空间实体Pi代表一个顶点；令Global＿Mean（DT）表示Delaunay三角网所有边长的平均值，Local＿Mean（Pi）表示与空间实体Pi相连所有边长的平均值，Global＿Variation（DT）表示Delaunay三角网所有边长的标准差，Local＿Variation（Pi）表示与空间实体Pi相连的所有边长的标准差。对任一空间实体Pi，整体边长约束准则可表述如下：

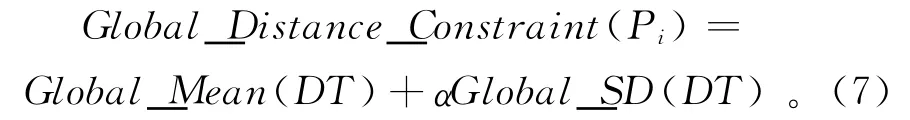
在Delaunay三角网中，如果与Pi直接连接的边的长度≥Global＿Distance＿Constraint（Pi），则将该边从三角网中删除。删除整体长边后，仍然存在一些局部长边，因此需要进一步施加局部边长约束。

假定图Gi为施加整体边长约束后得到的任意子图，Pj为Gi中的一个顶点，2＿Order＿Mean（Pj）是Pj的2阶领域内所有边长的平均值，Mean＿Variation（Pj）是与Pj直接相连边的方差的平均值，则局部边长约束可表述为

一般令β＝2。对于Gi中任意空间实体Pj，如果其2阶邻域内边的长度大于或等于Local＿Distance＿Constraint（Pj），则将该边从三角网中删除。通过局部修整，会让实体的空间邻近关系得到更好的确定［26］。

在施加整体和局部边长约束后获得的子图C＿DT中，对于任一空间实体Pj，所有与Pj直接通过边连接的实体构成了Pj的空间邻近域。依据上述方法构建的空间邻近域能够适应空间数据的密度差异，且避免了人为输入参数的干扰。

2.2 顾及非空间属性的空间聚类

为了方便进行非空间属性的距离计算，采用欧氏距离来表示顾及非空间属性的空间实体的非空间属性距离，用Dist（Pi，Qi）表示，同时用T表示非空间属性相似性的阈值。在构建空间邻近域后，下一步就是进行顾及非空间属性的空间聚类分析，在此之前先给出几个定义。

定义1空间邻域：对于C＿DT中的任一实体Pi，与其直接通过公共边相连的空间实体的集合成为Pi邻域，记为Neighbors（Pj）。

图3 基于0－1测试的Chebyshev映射Fig.3 Chebyshev Map tested by 0－1algorithm

定义2空间直接可达：对于C＿DT中的任一实体Pi，如果Qi∈Neighbors（Pj），并且Dist（Pi，Qi）≤T，则称Qi和Pi空间直接可达。

定义3空间可达：对于一个空间实体集CLU（其中CLU中的实体个数大于等于2），如果实体Qi满足以下2个条件，则称实体Qi与集合CLU空间可达：

①Qi∈Neighbors（Pi），且Pi∈CLU；

②Dist（Qi，Avg（CLU））≤T，其中Avg（CLU）为CLU中所有实体的非空间属性值平均值。

空间可达是用来计算某个空间实体与某空间实体集的相似度，它考虑到了局部和全局的差异性。

定义4密度指数：对于图C＿DT中的实体Pi，用DI（Pi）表示Pi的密度指数，即

式中：Nsdr（Pi）表示与实体Pi空间直接可达的实体个数；N（Pi）表示Neighbors（Pj）中的实体个数。

定义5空间聚类核：在未进行聚类的所有实体中，密度指数最大的空间实体称为空间聚类核。若最大密度指数的实体不止一个，则选择相应邻域实体之间平均非空间属性差异最小的的实体作为空间聚类核。

定义6扩展核：对于图C＿DT中的任意实体Pi，若在其邻域Neighbors（Pi）中至少有一个实体与Pi空间直接可达，则称Pi为一个扩展核。

顾及非空间属性空间聚类的主要步骤：①选择一个空间聚类核Pi，在其邻域Neighbors（Pi）中，对未聚类的扩展核根据密度指数进行排序；②在Neighbors（Pi）中，将同时满足空间直接可达和空间间接可达的扩展核按照密度指数从大到小的顺序与Pi聚到一起，形成初始簇；③以加入到初始簇里的扩展核为新的中心，按照①和②的策略继续扩展；④当没有实体可以加入到以Pi为空间聚类核的簇时，一个空间簇形成；⑤迭代进行①—④操作，当所有实体都进行遍历时，聚类结束。没有加入到任何簇的实体标识为噪声点。

3 结果与分析

3.1 中国降水0－1混沌识别

本次研究令随机数c的个数Nc为8 000，运用0－1测试方法对全国640个月降水序列进行测试，分别得到各气象站均方位移M（n）的渐近增长率K。640个气象站中，K最小值为西藏定日站的0.960 2，最大值为新疆伊宁站的0.994 5，平均值为0.984 0。以K值最小的西藏定日站为例说明中国各气象站月降水序列混沌特性。从定日站的p－q轨迹相图（c＝2.5）、M（n）－t关系曲线图和Kc－c散点图（图4）可以看出：p－q表现出布朗运动；M（n）随时间呈现出明显的线性增长；Kc的中位值K趋近于1。结果表明，各气象站月降水序列均表现出混沌特性。

运用Kriging方法对各气象站的K值进行空间插值，得到全国K值分布（图5）。由图5可知，K值分布具有明显的空间集聚特征。从大尺度来看，全国K值分布可分为4个区域，即西北高值区、南方次高区、华北—东北中值区和青藏低值区；从小尺度来看，局部区域K值也存在明显的空间变异，如东北地区中部K值较低，而东部和西部K值较高，又如华北地区以燕山山脉为界，山北K值较高，山南K值较低，再如祁连山北的K高值区和山南的K低值区。从整体上看，虽然华北—东北区和青藏区K值较低，但是空间上变异更强烈。

3.2 中国降水混沌空间聚类

利用插值方法对K进行空间插值，能够直观地给出K值的整体变化趋势，但是，在边界以及气象站分布空洞区域会存在较大误差，同时也很难给出更细致的K值分区，因此考虑运用空间聚类方法来进行进一步的研究。传统的聚类方法大都适用于空间目标分布比较均匀的情况。当目标分布不均时，使用全局固定的阈值（或参数）进行聚类，对于目标分布较密集的区域容易实现聚类目标，但是在目标分布较稀疏的区域，就可能产生大量的孤立点［30］。DBSC方法既能够在空间局部密度较高区域发现聚类，也能在空间局部目的较低区域发现聚类，并且能够适应空间局部密度的变化，在不同密度过渡区域发现不同聚类［30］，因此DBSC方法能够很好地适应中国气象站分布密度的东西部差异。

运用DBSC方法对带有K值属性的640个气象站进行空间聚类。首先采用Delaunay三角网构建邻近关系，并加以整体边长和局部边长约束，得到空间聚类的邻近域（图6）。在空间邻近域构建的基础上，进行顾及K值属性的空间聚类，得到聚类结果（图7），全国共分出了29个空间簇（C0表示离散点或噪音点）。从结果看，空间簇内的差异较小，而簇间的差异较大。南方次高区空间簇数较少，大部分形成单一簇（C1），说明其降水混沌度空间变异小；西北高值区主要形成2个主要簇，即新疆地区的C7、祁连山以北沿河西走廊一线的C10；东北—华北区和青藏区分簇数较多，这也反映出这2个区混沌度存在比较强烈的空间变异，与前文的插值结果相吻合；东北地区主要3个大簇，分别为C4（黑龙江中南部、吉林中部、辽宁东部）、C12（吉林东部、黑龙江东部长白山区）和C9（辽宁中西部、吉林西部、内蒙古东部大兴安岭）；华北地区空间簇划分结果更复杂，主要有C3（山东半岛、辽东半岛南部）、燕山以北的C21、阴山以南的C8以及太行山区的C14；青藏区主要有C5（云贵高原西部）、C11（三江源地区）、C13（柴达木盆地）、C16（四川中南部）、C20（西藏中部）；其余各簇均在局部小范围存在。

图4 月降水序列0－1混沌识别（以定日站为例）Fig.4 Chaos test for monthly precipitation time series based on 0－1method（Take Dingri Station for example）

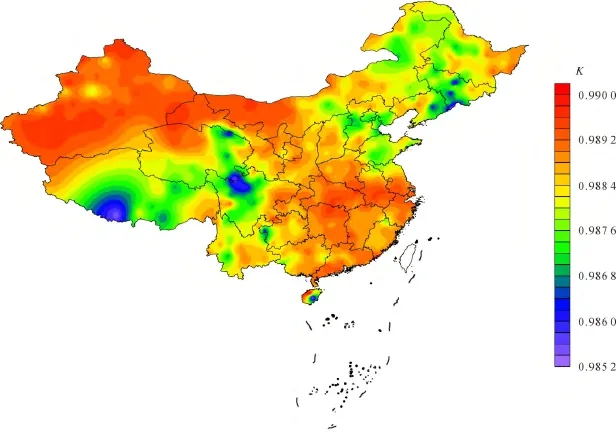
图5 全国K值分布Fig.5 K－value distributions of China

图6 空间邻近域构建Fig.6 Construction of the spatial neighborhood

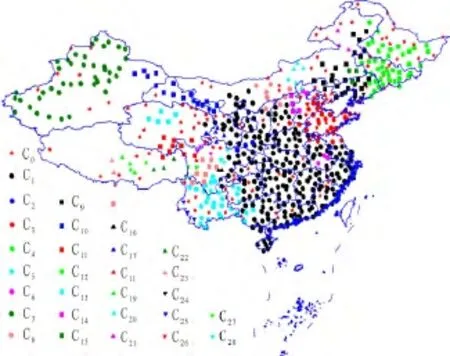
图7 中国降水混沌DBSC聚类结果Fig.7 Spatial clustering result of chaos for precipitation data in China

3.3 中国降水混沌动力系统分析

降水系统受到多个驱动系统影响，它们之间以某种或多种方式发生复杂的非线性和非平衡的相互作用，形成各种时空图样，在一定的时空范围内具有明显的层次性。系统的整体行为并非简单地与子系统的行为相联系［31］，而是表现出整体趋势的规律性。从气候尺度来看，降水系统的动力学特征首先是由其所在的大气候类型决定。由于海陆、地形、环流等众多因素的影响，中国气候变化十分复杂，但是从整体上来说，全国有4种主要的气候类型，即西北地区的温带大陆性气候、东北和华北地区的温带季风气候、南方地区的亚热带－热带季风气候和青藏高原的高原性气候。而中国各气象站降水序列0－1混沌测试的K值的空间插值和聚类结果在大尺度上均反映了这4种气候类型。

西北地区温带大陆性气候，降水主要受西风带影响，多属于干旱半干旱地区，年降水量少，年际和月际变化率大（如新疆喀什站年降水的平均距平率达40%，而吉林通化站仅为14%），因此月降水序列表现出最高的混沌度；南方地区受东亚季风、南亚季风、副热带高压、青藏高原积雪等多种气象因素的影响，也是我国受台风影响最严重的区域，再加上复杂的地形条件，使得月降水序列也具有较高的混沌度；华北—东北区降水也主要受南亚季风和东亚季风的影响，但是本区南亚季风已经减弱，而且本区地形条件远比南方地区简单，平原面积比重较大，因此降水混沌度比南方地区要小；青藏区虽然也受西风带的影响，因青藏高原的阻隔，高原地区的西南地区风速较小，高原东侧位于西风的背风侧，降水主要受南亚季风的影响，降水系统相对简单，因此青藏区降水序列的混沌度相对较低。

从降水混沌聚类的结果来看，地形条件是局部地区降水混沌变异的重要因素。沿祁连山北侧成条带状的C10簇、柴达木盆地的C13簇、三江源的C11簇、燕山以北的C21簇、长白山区的C12簇、大兴安岭的C9簇等均与地形条件密切相关。

4 讨论与结论

4.1 讨论

1）0 －1混沌测试方法是一种新的快速有效的混沌识别方法，它直接对数据进行计算，不需要传统混沌识别方法的相空间重构。已有的文献［15－22，32］均将其作为一个二元混沌识别方法，但是通过对中国640个气象站的月降水序列进行0－1混沌测试，发现其空间插值和聚类结果具有明显的空间变异规律，而且此规律与中国的大气候类型特征以及局部地形变化吻合较好，这就说明了0－1混沌测试方法具有反映系统混沌度的特性。目前还没有相关文献对其是否能够反映系统的混沌度进行过理论阐述，在以后的研究中，还需加强其理论意义的深度研究。

2）由于自然条件、交通等原因，中国气象站点分布密度不均，东部地区气象站点密度大，且分布均匀，而在新疆、西藏、青海、内蒙古、黑龙江北部等区域存在数量较多、范围广的气象站分布空洞，这就影响了插值和聚类的准确度，需要进一步地细化研究。

3）对降水系统进行空间聚类，既要考虑空间上的邻近性，还得考虑非空间属性的相似性，同时由于降水系统的影响因素十分复杂，要求聚类方法要适应空间数据的复杂分布，能够区分可能存在的噪声点。DBSC方法采用边长约束的Delaunay三角网来描述气象站点间的空间邻近关系，顾及混沌属性进行空间聚类。从中国降水混沌的空间聚类结果来看，DBSC方法有效地实现了降水混沌的空间变异区分。

4.2 结论

1）通过0－1混沌测试方法的识别，中国640个气象站的1960—2011年月降水序列的K值均趋近于1，表现出明显的混沌特性，同时中国降水混沌的空间插值和聚类结果表明，0－1混沌测试方法具有反映系统混沌度的特性。

2）根据中国各气象站K值的插值结果，西北区降水序列表现出最高的混沌度，南方区次之，华北－东北为中值区，青藏高原为低值区；运用DBSC方法将全国分成了29个空间簇。降水序列混沌度的空间插值和聚类结果从大尺度上与中国的大气候分区相对应，从小尺度上又反映了局部降水动力系统特征。

3）本次研究从一个全新的角度对中国各地区降水的内在规律做了初步探讨。联合运用0－1混沌方法和DBSC空间聚类方法，不仅能够研究不同空间尺度的降水规律，还能够通过不同时期和阶段的对比来研究降水系统混随时间的变化规律，这为降水动力系统的时空规律研究提供了一条新的途径和方法。

（References）：

［1］Millán H，Rodríguez J，Ghanbarian－Alavijeh B，et al.Temporal Complexity of Daily Precipitation Records from Different Atmospheric Environments：Chaotic and Lévy Stable Parameters［J］.Atmospheric Research，2011，101（4）：879－892.

［2］王红瑞，宋宇，刘昌明，等.混沌理论及在水科学中的应用于存在的问题［J］.水科学进展，2004，15（3）：400－407.Wang Hongrui，Song Yu，Liu Changming，et al.Applilcation and Issues of Chaos Theory in Hydroscience［J］.Advances in Water Science，2004，15（3）：400－407.

［3］姜翔程.水文时间序列的混沌特性及预测方法［M］.北京：中国水利水电出版社，2011：13－15.Jiang Xiangcheng.Chaotic Characteristics of Hydrological Time Series and Prediction［M］.Beijing：China Water Power Press，2011：13－15.

［4］袁鹏，李谓新，王文圣，等.月降雨量时间序列中的混沌现象［J］.四川大学学报：工程科学版，2002，34（1）：16－19.Yuan Peng，Li Weixin，Wang Wensheng，et al.Chaos Analysis of Monthly Precipitation Time Series［J］.Journal of Sichuan University：Engineering Science Edition，2002，34（1）：16－19.

［5］李眉眉，丁晶，王文圣，等.基于混沌理论的径流降尺度分析［J］.四川大学学报：工程科学版，2004，36（3）：14－19.Li Meimei，Ding Jing， Wang Wensheng，et al.Downscaling Analysis of Runoff Based on the Chaos Theory［J］.Journal of Sichuan University：Engineering Science Edition，2004，36（3）：14－19.

［6］陈社明，卢文喜，罗建男，等.吉林西部气象干旱的多标度分形特征［J］.吉林大学学报：地球科学版，2013，43（1）：243－250.Chen Sheming，Lu Wenxi，Luo Jiannan，et al.Multifractal Characteristic of Meteorological Drought in Western of Jilin Province［J］.Journal of Jilin University：Earth Science Edition，2013，43（1）：243－250.

［7］Strogatz S.Nonlinear Dynamics and Chaos：With Applications to Physics，Biology，Chemistry and Engineering［M］.New York：Perseus Books Group，1994：366.

［8］Zeeb S，Dahms T，Flunkert V，et al.Discontinuous Attractor Dimension at the Synchronization Transition of Time－Delayed Chaotic Systems［J］.Physical Review E，2013，87（4）：2910.

［9］牛宁.中国东部夏季降水各向同性分区及其气候学特征［D］.兰州：兰州大学，2007.Niu Ning.The Partition of East China Based on the Summer Rainfall Isotropy and Its Cliamatological Analysis［D］.Lanzhou：Lanzhou University，2007.

［10］刘扬，韦志刚，李振朝，等.中国北方地区降水变化的分区研究［J］.高原气象，2012，31（3）：638－645.Liu Yang，Wei Zhigang，Li Zhenchao，et al.Study on Division of Precipitation in Northern China［J］.Plateau Meteorology，2012，31（3）：638－645.

［11］Chen Liyuan，Chen Deling，Wang Huijun，et al.Regionalization of Precipitation Regimes in China［J］.Atmospheric and Oceanic Science Letters，2009，2（5）：301－307.

［12］秦爱民，钱维宏.近41年中国不同季节降水气候分区及趋势［J］.高原气象，2006，25（3）：495－502.Qin Aimin，Qian Weihong.The Seasonal Climate Division and Precipitation Trends of China in Recent 41Years［J］.Plateau Meteorology，2006，25（3）：495－502.

［13］崔瀚文，姜琦刚，邢宇，等.32a来气候扰动下中国沙质荒漠化动态变化［J］.吉林大学学报：地球科学版，2013，43（2）：582－591.Cui Hanwen，Jiang Qigang， Xing Yu，et al.Dynamics of Sandy Desertification Under Climate Disturbance in China from 1975to 2007［J］.Journal of Jilin University：Earth Science Edition，2013，43（2）：582－591.

［14］Orrell D.Role of the Metric in Forecast Error Growth：How Chaotic is the Weather［J］.Tells A，2002，54（4）：350－362.

［15］Gottwald G A，Melbourne I.A New Test for Chaos in Deterministic Systems［J］.The Royal Society，2003，460（2042）：603－611.

［16］Gottwald G A，Melbourne I.Testing for Chaos in Deterministic Systems with Noise［J］.Physica D：Nonlinear Phenomena，2005，212（1/2）：100－110.

［17］Gottwald G A，Melbourne I.On the Implementation of the 0－1Test for Chaos［J］.SIAM Journal on Applied Dynamical Systems，2009，8（1）：129－145.

［18］Sun Kehui，Liu Xuan，Zhu Chongxu.The 0－1Test Algorithm for Chaos and Its Applications［J］.Chinese Physics B，2010，19（11）：510.

［19］Falconer I，Gottwald G A，Melbourne I，et al.Application of the 0－1Test for Chaos to Experimental Data［J］.Society for Industrial and Applied Mathematics，2007，6（2）：395－402.

［20］Litak G，Syta A，Wiercigroch M.Identification of Chaos in a Cutting Process by the 0－1Test［J］.Chaos，Solitons ＆ Fractals，2009，40（5）：2095－2101.

［21］Krese B，Govekar E.Nonlinear Analysis of Laser Droplet Generation by Means of 0－1Test for Chaos［J］.Nonlinear Dynamics，2012，67（3）：2101－2109.

［22］李新杰，胡铁松，郭旭宁，等.0－1测试方法的径流时间序列混沌特性应用［J］.水科学进展，2012，23（6）：861－868.Li Xinjie， Hu Tiesong， Guo Xuning，et al.Application of the 0－1Algorithm for Chaos to Runoff Time Series［J］.Advances in Water Science，2012，23（6）：861－868.

［23］Feigenbaum M J.Quantitative Universality for a Class of Nonlinear Transformations［J］.Journal of Statistical Physics，1978，19（1）：25－52.

［24］王文圣，向红莲，赵东.水文序列分形维数估计的小波方法［J］.四川大学学报：工程科学版，2005，37（1）：1－4.Wang Wensheng，Xiang Honglian，Zhao Dong.Estimating the Fractal Dimension of Hydrological Time Series by Wavelet Analysis［J］.Journal of Sichuan University：Engineering Science Edition，2005，37（1）：1－4.

［25］Ghorbani M A，Kisi O，Aalinezhad M.A Probe into the Chaotic Nature of Daily Stream Flow Time Series by Correlation Dimension and Largest Lyapunov Method［J］.Applied Mathematical Modeling，2010，34：4050－4057.

［26］Liu Qiliang，Deng Min，Shi Yan，et al.A Density－Based Spatial Clustering Algorithm Considering Both Spatial Proximity and Attribute Similarity［J］.Computers ＆ Geosciences，2012，46：296－309.

［27］Deng Min，Liu Qiliang，Cheng Tao，et al.An Adaptive Spatial Clustering Algorithm Based on Delaunay Triangulation［J］.Computers，Environment and Urban Sytems，2011，35：320－332.

［28］石岩，刘启亮，邓敏，等.融合图论与密度思想的混合空间聚类方法［J］.武汉大学学报：信息科学版，2012，37（11）：1276－1280.Shi Yan，Liu Qiliang，Deng Min，et al.A Hybrid Spatial Clustering Method Based on Graph Theory and Spatial Density［J］.Geomatics and Information Science of Wuhan University，2012，37（11）：1276－1280.

［29］Tsai V J D.Delaunay Triangulations in TIN Creation：An Overview and a Linear－Time Algorithm［J］.International Journal of Geographical Information Systems，1993，7（6）：501－524.

［30］李光强，邓敏，刘启亮，等.一种适应局部密度变化的空间聚类方法［J］.测绘学报，2009，38（3）：255－262.Li Guangqiang，Deng Min，Liu Qiliang，et al.A Spatial Clustering Method Adaptive to Local Density Change［J］.Acta Geodaetica et Cartographica Sinica，2009，38（3）：255－262.

［31］Fang J Q，Chen G.Some General Features of Complexity and Its Control and Ant Control Strategies［C］//Sun Zuxun.Proceedings on Sino－German Symposium on Complexity Scienc.Beijing：China Institute of Atomic Energy，2000：163－172.

［32］Gottwald G A，Melbourne I.Comment on“Reliability of the 0－1Test for Chaos”［J］.Physical Review E，2008，77（2）：028201.