橡胶“热缩冷胀”的实验研究及其热力学分析＊

毛俊雯，罗 骏，徐 燕，许丹丹，任文英

（湖州师范学院 理学院，浙江 湖州313000）

和通常人们对一般固体“热胀冷缩”的预期相反，处于拉伸状态的橡胶，加热后会出现收缩的现象，称为Gough－Joule效应［1～2］.这是因为橡胶具有独特的力学性质——高弹性.橡胶弹性理论认为，橡胶的高弹性主要来自于构象熵的改变.橡胶中分子链不停地运动，而化学键键长和键角基本不变.当受到外力的拉伸时，分子链就会伸展开来，构象数下降，熵减小.而加热有利于分子运动，使熵值增加，从而利于收缩［3～4］.

热力学分析给出的橡胶状态方程为［3］：

近年来，已经有一系列实验用来演示橡胶高弹性的特点.例如橡胶张力和温度的关系、张力和伸长变化关系的测量［5～6］.Liff小组［2，7］设计了一系列的实验演示拉伸状态下橡皮圈的热收缩效应，但是没有测量温度、张力和伸长等物理量之间的定量关系，因而无法对熵弹性进行理论分析.本文设计实验对橡胶热收缩现象进行教学演示，测量了恒定外力下橡皮圈伸长量和温度的关系，并从热力学角度证明橡胶的“热缩冷胀”正是熵弹性的体现.另外，利用这一实验结果以及偏微商循环关系，得到了内能贡献和张力的比值fe／f在20%左右.

1 实验设计

实验主要利用改装的焦利秤，用金属丝代替原来的弹簧，金属丝下挂一条下端挂有重物的橡皮圈，使橡皮圈处于拉伸状态，如图1所示.在橡皮圈下端悬挂重物的地方做一个标记金属丝，使读数更加精确.将拉伸的橡皮圈完全浸没在盛水的大量筒中，水温变化时，橡皮圈长度发生变化，标记金属丝的位置也将随之发生改变.这一装置可以很好地演示橡胶的“热缩冷胀”过程.多次重复测量，即可得到橡皮圈在不同温度下的长度与温度的关系.

图1 实验装置示意图Fig. 1 The schematic plot of the experimental facilities

2 实验结果和分析

实验中通过水浴的方法改变水槽中的温度，得到不同外力下橡皮圈伸长比λ＝l／l0和温度的关系，如图2所示.我们采用经过预拉伸4～8h的橡皮圈，测量时从低温（10°C）开始，先升温到60°C，再降温回到初始温度，如图2中箭头方向.

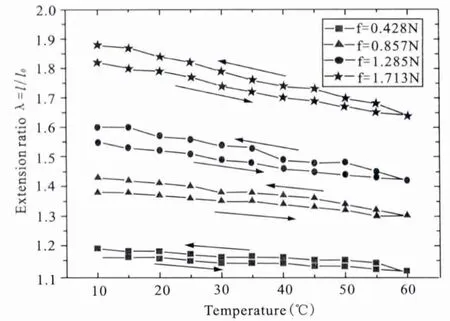
图2 实验装置示意皮圈伸长率度和温度的12Fig. 2 The extension ratio 度as a function of temperature for different tensile forces

从图2中可以看到，恒定外力下，随温度升高时，橡皮圈伸长比λ不断减小，橡皮圈收缩.当温度达到最高点后开始降温，此时橡皮圈伸长比反而增大，橡皮圈逐渐伸长.这一结果和人们通常预期的“热胀冷缩”完全相反.进一步可以看到，张力f增大，伸长比λ变化也增大，橡皮圈收缩越明显.

值得注意的是，在升温和降温这两个过程中，橡皮圈伸缩路径并不重叠.我们知道，橡皮圈从一种平衡状态过渡到另一平衡状态，既有热平衡的建立，又有力学平衡的建立.橡皮圈中分子链达到与外力相适应的平衡态需要很长时间［3］，而实验测量的等待时间是有限的，这就有可能使得处于相同温度和外力的拉伸状态，稍后测量得到的拉伸长度较长.文献［5］中橡皮圈的张力和伸长的关系体现了这一力学弛豫效应.实验中也发现，图2中如果降温到最低温度以后继续升温，再次回到某一温度时，橡皮圈的伸长和之前同一温度下两次测量得到的值相比都要长.与之相反，由于拉伸的橡皮圈具有“热缩冷胀”的特性，热平衡的弛豫将使得橡皮筋经历升温和降温过程恢复到原先温度时，其长度小于之前的值.由此我们可以推断，橡胶力学平衡的弛豫时间远远大于热平衡弛豫时间.

3 热力学分析

考虑橡胶形变是可逆的这一理想情况，可以对橡胶的状态变化进行热力学分析.近似认为橡胶是不可压的，其体积变化为零.由此，热力学第一定律表达为：

结合S＝S（T，f），l＝l（T，f），可以得到：

从而橡皮圈长度随温度变化的关系l＝l（T）为：

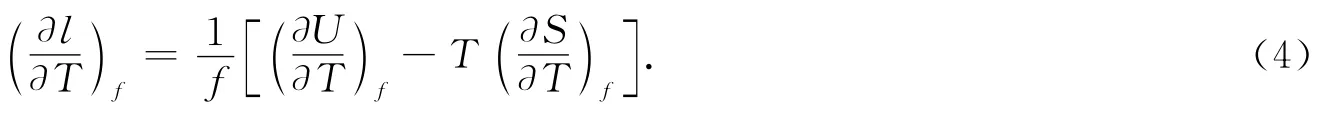
4 内能变化对弹性力的贡献

接下来讨论如何利用上面的实验结果得到内能贡献.

根据l，f，T三个变量间满足的偏微商循环关系式，张力f随温度T的变化可以表示为橡皮圈的热膨胀（收缩）特性和力学性质乘积的负值，如式：

5 结论和讨论

经实验测量恒定外力下橡皮圈的伸长和温度的关系，我们发现张力越大，热缩现象越明显，并通过热力学分析证实了橡胶的“热缩冷胀”正是熵弹性的体现.对实验数据进一步分析我们还得到内能贡献fe／f大约为20%.

橡胶的热力学分析表明，橡胶的状态方程（1）具有和范德瓦尔斯气体状态方程类似的形式，表明固体橡胶具有类似气体的一些性质.如果忽略内能的长度效应，那么就得到理想橡胶的状态方程，这和理想气体的情况完全类似.

图3 不同伸长比λ=l/ l0对应的内能贡献比fe/f Fig.3 The portion of internal contribution fe/f atdifferent exension ratios λfor temperature T = 10 ℃，3 0℃

由于橡胶形变所需时间很长，图2实验用的橡皮圈在实验前已经处于完全拉伸状态约8～10h.实验中我们发现，没有预拉伸的橡皮圈热收缩现象不明显.这是因为橡胶高弹形变所需时间很长，由于实验过程中的形变相对于外力作用下产生的形变小很多，所以预拉伸可以减少实验过程中橡胶达到平衡的时间，从而减少实验误差.

文中对内能贡献的讨论主要从热力学角度进行分析，对橡胶熵弹性更深入的理解，需要通过橡胶的弹性统计理论.

［1］Treloar L R G.The elasticity and related properties of rubbers［J］.Rep Prog Phys，1973（36）：755－826.

［2］Liff M I.Polymer physics in an introductory general physics course［J］.The Physics Teacher，2004（42）：536－540.

［3］何曼君，张红东，陈伟孝，等.高分子物理［M］.上海：复旦大学出版社，2007.

［4］何平笙，朱平平，杨海洋.如何理解橡胶高弹性的特点［J］.高分子通报，2009（12）：68－71.

［5］Roundy D，Rogers M.Exploring the thermodynamics of a rubber band［J］.American Journal of Physics，2013（1）：20－23.

［6］周旭章.橡胶拉伸过程的热力学实验［J］.大学化学，1996（3）：45－47.

［7］Liff M I.Another demo of the unusual thermal properties of rubber［J］.The Physics Teacher，2010（48）：444－446.