高校学生课程考试成绩的正态化换算方法研究

许年春，刘东燕，夏文静，黄林青

考试是检验学生学习成果的方法，课程考试分数是评判学生课程知识掌握程度的主要依据。高校考试试题的难度以能使大多数学生达到教学大纲规定的基本要求为宜，学生成绩分布也应呈正态分布，即高分和低分人数少，中间分数段人数多。然而，由于各方面的原因[1-4]，现实中学生考试分数往往不服从正态分布，有时甚至偏离很大。

一、高校学生考分换算的必要性

考分换算是指按一定的规则对学生考试的原始分数进行转换计算，从而得到另一个更能满足要求、更合理的分数。与中小学校相比，高等学校学生考分换算更显必要。

第一，考分换算是科学评定学生奖学金的基础。学习成绩是高校评定学生奖学金最重要的依据。目前，我国高校在计算学生学习成绩时普遍采用的是加权平均绩点计算法，即对学生各门课程的成绩绩点按学分加权后求和，再除以总的学分。比如重庆科技学院的学生课程成绩换算办法：60分以下绩点为0；60分以上，绩点等于所得分数减去50后再除以10。采用五级评分制时，不及格、及格、中等、良好和优秀所对应的绩点分别是 0、1.5、2.5、3.5和 4.5。

大学四年学生学习的课程有数十门，各门课程的性质和特点不一样，考核方式不一样，试卷命题人和阅卷人不一样，这些都将导致不同课程的成绩分布差异。非试卷考核课程（如实践课）主要采用五级评分制，许多高校对教师给出的评分有定量的规定，如优秀率不得超过20%，优秀和良好率不得超过60%。对试卷考核课程则无法作此类规定，因为所有的评分都必须依照事先做好的标准答案来。当然，在评定主观题时阅卷教师有一定的自由裁量空间，但这只能使总体分数上下整体移动，不能调节分数分布形态，最后的结果是考试分数的分布形态各异，作出的分数分区图五花八门。在填写试卷与成绩分析表时，任课教师必须对考试分数分布不符合正态分布的原因作出说明，提出改进措施。但这种要求没有什么效果，因为下次考试时很多因素又发生了变化。

对成绩分布形态各异的数十门课程绩点加权求和后排序，运用数学知识可以证明这种算法的不科学。平均加权绩点计算法本身是科学的，错就错在没有事先对考试分数进行换算。

第二，考分换算可提高学生评教结果的可信度。学生评教制度是高校保障教学质量的重要制度。我国高校的评教活动始于20世纪80年代[5]，此后，随着高校教学工作水平评估的普遍开展，教学管理中的质量控制工作受到重视，学生评教也逐步得到系统的、规范的开展。如今很多高校开发了学生网上评教系统，部分高校建立了评教公示制度，将评教结果以学校文件的形式在全校公布。有的高校根据学生评教情况建立了教师激励机制，将学生评教结果与教师职称晋升及课酬、津贴等挂钩，对教师进行奖励和惩戒。

作为高校教学质量保障体系中的一项重要制度，学生评教应该规范组织，严谨实施。学校管理层在组织学生评教时应该小心谨慎、考虑周全，既要维护学生的合法权益，让学生敢于表达自己的真实看法，又要维护教师的合法权益，保障师道尊严，不能让教师因担心学生评教给低分而放低身段，对学生百般迁就，不敢批评违反纪律的学生。

学生评教结果的可信度既取决于评教活动组织实施是否规范严谨，又取决于学生评教时的心态。学生填教学评估问卷表是在表达他的主观意志，一方面他意识到自己应该按问卷表中的内容逐项进行客观选择，另一方面问卷表内容以外的因素又会不可避免地影响他的选择。其中一个最重要的因素是考试分数，因为分数决定着学生的一切。有些教师为了讨好学生或预防不及格率过高，故意降低试卷难度，或者考前组织针对性的复习，结果学生普遍考得高分，这样他在学生评教时就比其他教师占有明显的优势。这就是常说的“高分互换”现象[6-8]。相反，如果某门课学生考试分数普遍低下，任课教师在学生心目中的形象则可能一落千丈。为了防止这种情况发生，有些学校将评教活动安排在考试之前，或者设定学生只有在评教完后才能看到考试分数。但这同样不能解决问题，因为学生可以通过上一年级的学生了解上次的考试结果。还有一些教师可能是第二次给某班学生上课，第一次的考试分数也将影响第二次评教。同时这样做还会带来一些操作上的困难，如一学期各门课的结束时间和考试时间不同，而评教活动只是在期末组织一次。

实行考分换算后，情况就不一样了。某门课程某学生考了80分，但这并不一定能说明他考得好，因为可能全班一半的同学都在80分以上。先对各门课程的学生考试分数进行统一换算，使最高分和分数分布形态一致，学生评教时就可能不会受分数的影响。

第三，考分换算有利于国际合作培养人才工作的顺利实施。国际合作培养人才已成为当代中国高等教育发展的一种趋势，各高校都在积极争取与国外知名高校联合培养人才。培养层次包括专科、本科和研究生。本科阶段的培养模式有“3+1”（国内3年国外 1 年）模式、“2+2”模式和“1+3”模式等，学生完成规定的课程和学分，毕业答辩合格，可获得双方的毕业证书。

考虑到绝大多数学生的外语背景，学校在选择国外合作高校时以英语语系国家为主，最多的当属英国和美国。英国、美国的高校本科生毕业，其学士学位一般分为4等：一等荣誉学士学位（First-class honours），二等上荣誉学士学位（Upper Second Class Honours），二等下荣誉学士学位（Lower Second Class Honours），三等学士学位（Third Class Honours）。有些高校还设有及格学士学位。一等荣誉学士学位，要求学生全部课程的平均分在70分以上。二等上荣誉学士学位，要求是60～69分。二等下荣誉学士学位，要求是 50～59 分。三等学士学位，要求是 40～49 分[9]。中国学生觉得一等荣誉学士学位要求的分数很低，太好拿了。据英国高等教育统计局公布的数据，2010年全英国高校本土学生一等荣誉学位授予率是13%，而英国高校2008-2009年度国际学生获得一等荣誉学士学位的只有10%[10]。可见，全部课程的平均分在70分以上的只有极少数学生。中国的教育从小学开始就设定60分作为及格分，而英国小学生统考各科（英语、数学、科学）是以6分作为最高分，4分为及格分。中国高校教师在命题时是以大部分学生达到60分以上为目标，而英国教师在设计试卷和评阅试卷时则要控制70分以上人数。

国内外高校在学生课程考试分数认知、文化背景方面存在差异，这不可避免地会对联合培养人才、学位等级评定等方面带来麻烦。为保障合作教育的顺利实施，也有必要对学生的两地课程考分进行统一换算。

二、考分换算的三种方法

目前，常用的考分换算方法有三种。第一种为比例映射法[1]。这是一种最基本、最简单的考分换算方法。其算法如下：

考生某次考试的原始分（百分制）按由小到大顺序排列为集合X。

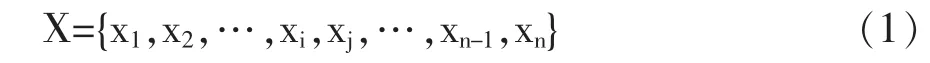
当要求最低分为y1、最高分为yn时，只需将x1直接换为y1，将xn换为yn，其余分数按照数学插值法换算成对应的分数，最后得到换算后的分数集合Y。

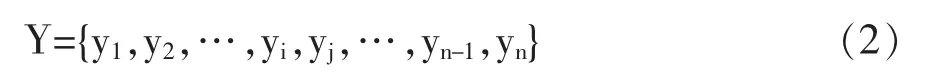
第二种为线性方程换算法（简称Y法）[2]。Y法其实质也是比例映算法，但它不是简单设定最高分和最低分，而是先以中国人习惯的60分和90分分别作为及格分和优秀成绩的标准，再参照正态分布曲线规律±1.96S占总面积的95%，这样，不及格与优秀成绩各占2.5%。建立方程组：

求得a和b，代入式（4），计算出换算分数Y。

第三种为Z分数换算法（简称Z法）[2-4]。其计算公式如式（5）。

三、考分正态化换算新方法

比例映射法只能整体改变分值的大小，无法将分数调节成正态分布。Y法的目的是控制60分以下和90分以上人数在一合理范围（但这一目的未必能实现），同样不能将分数调节成正态分布。大多数文献都将Z法得到的分数称为标准分[2-4]，实际上Z法得到的并不是一个百分制的分数，而是各考生分数在某课程考试分数中的位置标尺（无量纲），利用它在一定程度上可以消除不同课程分数分布的影响，实现不同课程间的成绩比较，但它同样无法得到一个正态化的百分制分数。

下面，提出一种可以实现考分正态化的换算新方法。

正态分布的密度函数如式（6）所示。

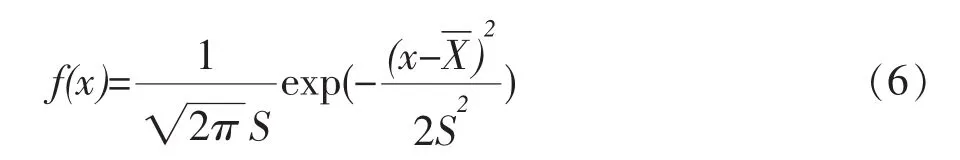
对式（6）左右积分，可得到正态分布的分布函数，如式（7）。分布函数曲线如图1所示。

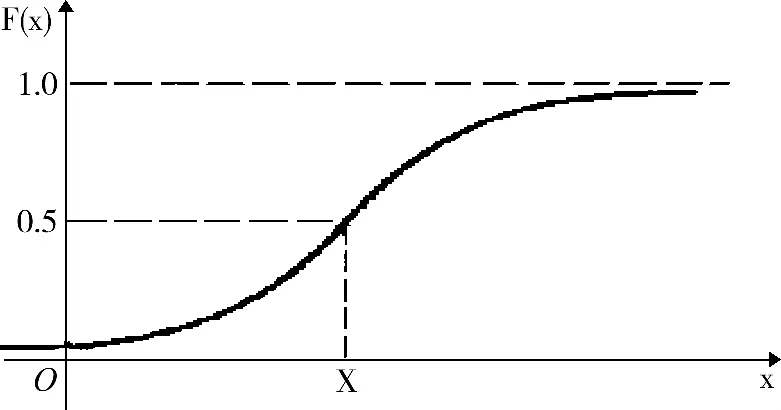
图1 正态分布函数曲线

考生某次考试的原始分，按由小到大顺序排列集合如式（1）；各原始分的重分个数（正整数）集合对应为式（8）。

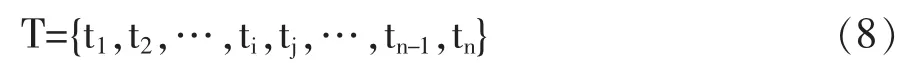
式中，tj表示有tj个考生的分数均为xj。

为控制不及格率，取一个低于60分的原始分xi作为换算后的及格分（当x1≥60时，将x1换算成60）。各门课程由相关主管部门统一设定一个最高分M，则xi以后各个原始分xj按式（9）进行计算，得到换算后的分数yj。

式中，Y=(60+M)/2；S为标准差。换算前试算出一个S值，使 yj=M 时，式（9）右边等于 1.0。

式（9）右边尽管不能得到积分解析式，但借助Excel或编程，可以快速得到计算结果。

四、换算实例

土木工程专业2009级1班共50名同学，“土力学与基础工程”课程考试的原始成绩如表1中第2列所列。由于试卷计算题较多，难度较大，不及格率达38%。为控制不及格率，经向学院申请，取48分作为换算后的及格分数（即60分）。假定学校统一规定各门课的最高分M=96分，平均分=（60+96）/2=78。经试算，取 S=9.0 时，F（96）=1.0。由式（9）可计算出正态化换算后的分数，如表1中第4列所列。

当采用比例映射法时，将48换成60，90换成96，其余通过数学插值法计算。换算出的比例映射分数如表1中第5列所列。

当采用 Y 法时，解式（3.1）、（3.2），得到 a=42.1，b=0.513。再由式（4）计算得出换算分数如表1中第6列所列。Y法的初衷是换算后90分以上的人数占2.5%，即1-2人。由表1可见，换算后最高分88.3分，没有90分以上的同学。这是因为式（3）、（4）只是从概率上保证2.5%，而实际的人数与每次换算的原始分有关。另外，原始分数36经换算成了60.6，及格原始分太低，不利于调动学生的学习积极性。

表1 学生考试分数换算结果

采用Z法换算的结果如表1中第7列所列，换算值有正有负。正数表示高于平均分，正数越大表示分数越高，表中最大值为1.738。负数表示低于平均分，负数越小表示分数越低，表中最小值为-2.218。Z法换算值不符合我们通常表示成绩的习惯，非专业人士（如学生家长、就业单位招聘人员）看起来费解。文献[2]提出，可将Z法换算值再次换算成百分制分数，换算方法还是线性插值。按照其给出的方法，以-1.078作为对应的及格分，换算结果如表1中第8列所列。比较第8列与第5列，发现两者一模一样。

为验证正态化换算的效果，分别绘出原始分、比例映射分和正态化换算分的各分数段人数图如图2。

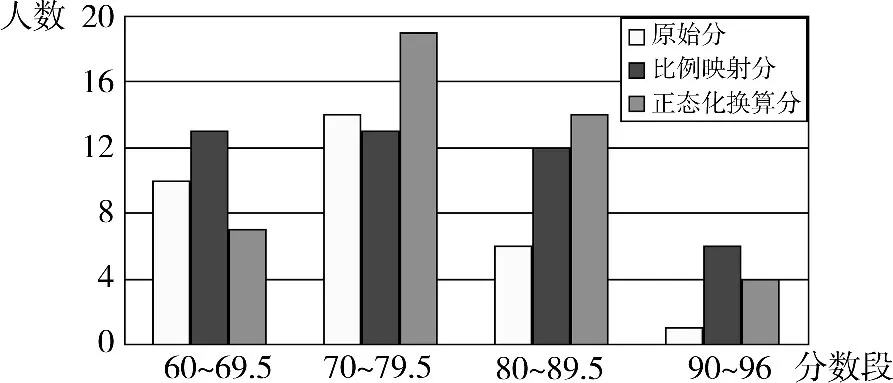
图2 各分数段人数柱状图

由图2可见，比例映射分只是简单的分数映射，无法调节分数分布形态，而采用正态化换算法，不仅能控制不及格率，还能将分数调节到正态分布形态。

为了进一步说明正态化换算方法的优越性，举一个极端的例子：

某班38名同学，某课程考试试卷难度系数较小，考分从80分到96分，每个分数值都有2名同学（即重分个数均为2），另外4名同学的分数由高到低分别是 78、72、66、60。显然，分数分布极其异常，80～96分数段占到了89%以上。采用比例映射法，没有任何效果。采用正态化换算方法，平均分=（60+96）/2=78。经试算，取 S=8.1 时，F（96）=1.0。经分数换算，分数分布为：60～69.5分数段 6人，70～79.5分数段 16人，80～89.5分数段12人，90～96分数段4人。分数分布十分正常。

最后，通过定性分析来加深对正态化换算方法的理解：当高分段或低分段分布人数很多时，1分的差距即意味着排名的悬殊。为控制该分数段的人数，原始分1分的差距，经换算后会则变成了几分的差距。

五、结论

采用正态化换算法对各门课程的考试分数进行换算，可使各门课程最高分相同，分数分布形态一致。这对科学评定学生奖学金、提高学生评教结果可信度和顺利实施国际合作联合培养人才工作，都有积极的意义。

[1]赵逸云，等.一种简单、可靠的分数正态化及标准化换算方法[J].云南大学学报：自然科学版，2004（B07）.

[2]严灿勋，刘慧敏.标准分在评定考试成绩中的应用[J].高教论坛，2010（5）.

[3]吴学芝.多学科综合成绩计算方法的研究[J].辽宁师专学报：自然科学版，2007（3）.

[4]李少荣.相对考试成绩与绝对考试成绩的应用[J].卫生职业教育，1996（5）.

[5]别敦荣，孟凡.论学生评教及高校教学质量保障体系的改善[J].高等教育研究，2007（12）.

[6]毛丰付.学生评教，偏差几何：对某校学生评教的数据分析[J].高等教育研究，2009（3）.

[7]Birnbaum M H.A survey of faculty opinions concerning studentevaluations ofteaching [EB/OL].http：//faculty.fullerton.edu/senatenews/page2.html.

[8]Isely P，Singh H.Do higher grades lead to favorable student evaluations[J].Journal of Economic Education，2005（1）.

[9]Course Guide for BEng （Hons） in Civil Engineering at London South Bank University[EB/OL].Department of Urban Engineering，Faculty of Engineering，Science and the Built Environment.2012-2013.

[10]西交利物浦大学：从优秀走向卓越[N].中国青年报，2011-06-08.