基于蒙特卡洛法的火灾情况下人员预期死亡风险评估

●孙 宽

(鹰潭市消防支队，江西鹰潭 335000)

(本栏责任编辑、校对 李 蕾)

0 引言

切实可行的建筑物火灾安全性能化设计离不开科学的火灾风险评估方法［1］，科学地预测人员火灾风险是选取合理的火灾安全设计方案的基础。在评估每个火灾场景可能造成的伤亡人数时，目前仅是通过比较必需安全疏散时间tRSET与可用安全疏散时间tASET两者的大小关系来确定人员能否逃生至安全区域［1－2］。然而，火灾与人员疏散均为十分复杂的过程，其中包含着诸多随机性因素。当前普遍采用的比较tRSET与tASET大小关系的方法，没有考虑各自的随机性因素，如tRSET中的火灾探测报警时间、人员预动作时间均取为定值，tASET仅考虑特定火灾场景下的火灾动力学特征［3-4］等等。这种方法对于评估可能造成的伤亡人数不够合理。

蒙特卡洛法是使用随机数处理确定性数学问题的方法，这一方法是在1945年左右由冯·诺伊曼(J．von．Neumann)和乌拉姆(S．M．Ulam)提出的。蒙特卡洛法可归结为三个主要步骤［3］:(1)构造或描述概率过程;(2)实现从已知概率分布抽样;(3)建立各种估计量，对模拟实验的结果进行考察和登记，从中得到问题的解。

本文研究着重于考虑人员疏散时间计算过程中火灾探测时间、人员预动作时间、人员疏散运动时间的随机性，并且通过蒙特卡洛模拟，求得整体安全疏散时间的分布。利用该分布的统计学意义，结合可用安全疏散时间的取值，来确定场所在某特定火灾场景下的预期死亡人数。

1 人员疏散时间的随机性分析

人员疏散时间可分为火灾探测报警时间、预动作时间、人员疏散运动时间。要对人员疏散时间进行随机性分析，就应当分别对这3个时间的随机性进行客观地分析。

1．1 火灾探测报警时间

火灾探测时间与报警时间主要受火灾发展初期动力学特征、起火区域的建筑环境与探测报警装置特性的影响。以感烟火灾探测器为例，工程计算将烟气高度沉降到房间高度的5%以下作为响应时间［2］。火灾烟气高度经验公式有以下假设:(1)房间的顶棚面积、地板面积以及各处标高相同;(2)火灾初期按照t2规律增长。

式中，Z为烟气层高度(m);td为火灾探测时间(s);Hr为房间净高(m);A为房间地板面积(m2)。

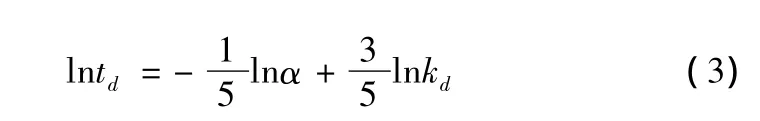
一般认为，火灾增长系数α服从对数正态分布［3］，故lnα服从正态分布。对于特定的建筑场景，kd为常量，lntd也服从正态分布。f(lntd)的平均值和标准差分别为:

1．2 安全疏散预动作时间

MacLennan et al．和Purser et al．通过火灾后问卷调查和事先未通知的疏散演习得到的数据表明，预动作时间为服从正态分布的随机变量［4-5］。

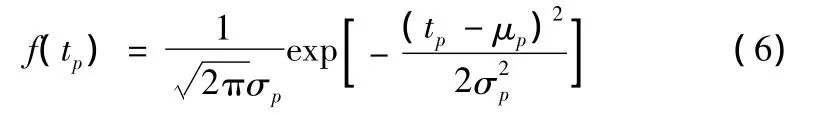
式中，f(tp)为预动作时间的概率密度函数;tp为预动作时间;μp为预动作时间的平均值;σp为预动作时间的标准差。

在此引用CFE模型［6］中的工程简化计算模型，作为预测火灾对人员造成的风险值中关于疏散准备时间的计算模型。

表1 不同功能建筑物采用不同火灾报警系统时的人员认识时间

无量纲参数a的影响因素为火灾发生时间，具体分为人员清醒时刻、休息或沉睡时刻;无量纲参数b的影响因素为火灾发生的场所，分为医院、商场和娱乐中心、办公楼及居民住宅区等;无量纲参数c的影响因素为火源位置或研究场所与火源之间的距离;无量纲参数d的影响因素为火灾强度;无量纲参数e的影响因素为报警装置和应急指挥系统的种类及其可靠性。各无量纲参数的取值见表2。

表2 人员疏散准备时间计算模型中的无量纲参数取值表

1．3 疏散运动时间

影响人员运动时间的参数主要包括人员总数、人员密度、人员行走速度、出口流量系数、有效出口宽度、最大疏散距离等。除有效出口宽度可以取为定值外，其它参数均为不确定变量。

1．3．1 人员密度

人员密度是疏散安全设计的基本参数。本文参照张树平等人在2002年分别以正常工作日、双休日及黄金周长假为调研时间［7］，对西安某场所的人数进行的实地调查，分析指出人员数量服从正态分布，得出了该场所疏散人数指标换算系数区间，见表3。

表3 不同楼层疏散人数指标换算系数上、下限

1．3．2 人员行走速度V

正常情况下，成人的行走速度大约在1．2 m·s-1左右。在火灾紧急情况下，由于人的恐慌心理，出现奔跑等紧急行为，逃生速度一般会大幅增加，这一方面会导致人员加速逃离危险区，缩短疏散运动时间，但同时可能造成过道局部或出口处的人员密度增加，从而导致行走速度下降。Predtechenskii和Milinskii［8］通过实验，研究了水平方向上人员行走速度与人流投影面积密度之间的关系，给出了经验公式，推荐过道上的人员行走速度为0．51～1．27 m·s-1，沿楼梯斜面的速度为0．36～0．76 m·s-1。在人员疏散过程中，人的行走速度显然不是一个常数，而是一个随机变量。

1．3．3 出口流量系数f

疏散出口流量系数代表了出口的通行能力，通常认为疏散出口流量与疏散出口的宽度成正比，流量系数是联系两者的比例常数，与人员密度、疏散速度以及出口的空间位置有关。我国现有的防火设计规范没有对其作出说明，当前的疏散时间分析中通常取1～1．3人·m-1·s-1［9］;国外学者 Hankin and Wright、Polus、Fruin和户川喜久二等人的研究表明疏散出口流量系数在某一范围内变化［10-12］，见表4。可以看出，在人员疏散过程中，疏散出口流量系数是一个随机变量。

表4 疏散出口流量系数的推荐值

1．3．4 最大距离D

房间内任一点到该房间直接通向疏散走道的疏散门的距离为疏散距离，在《建筑设计防火规范》(GB 50016-2006)中对民用建筑的最大安全疏散距离进行了相关规定。然而在实际当中，由于建筑内的各种物品占据空间，导致最大疏散距离并非可以直线距离计算，人在疏散时可能要绕障碍逃生，导致最大疏散距离大大增加，因此，最大疏散距离D是一个不确定变量。

2 火灾情况下可能导致的伤亡人数

人员伤亡预期风险评估一个基本的判据就是比较火灾危险状态来临时间与人员疏散时间的大小关系。如果人员在火灾到达危险状态之前未能全部疏散至安全区域，那么此时建筑物内剩余的人数即为在当前火灾场景下可能导致的伤亡人数。图1描述了可用安全疏散时间(tASET)和必需安全疏散时间(tREST)的关系。

图1 tASET和tREST的关系

在传统的人员火灾风险评估中，均未考虑火灾危险状态来临时间与人员疏散时间中的随机性。火灾探测报警时间、人员疏散准备时间与人员疏散运动时间均考虑为定值。从上文的分析中可以知道，火灾探测报警时间、人员疏散准备时间与人员疏散运动时间均为服从一定分布的随机变量。所以，可以据此利用相关的数学方法求得tREST的分布，并与可用安全疏散时间进行比较，对建筑物的火灾风险进行评估。

要求得某场所整体安全疏散时间的分布，需要先对探测报警时间、预动作时间、疏散运动时间的分布进行求解。其中探测报警时间可以依据文献［3］所给的分布，人员预动作时间可以依据 MacLennan et al．［4］和 Purser et al．［5］通过火灾后问卷调查和事先未通知的疏散演习得到的结论，而疏散运动时间则需要对场所进行疏散模拟得到其分布情况，在此选用Building EXODUS进行人员疏散的模拟。

一般认为，疏散运动时间呈正态分布［7］。通过安全疏散模拟可以得出某相应火灾场景下，人员疏散到安全区域的时间，并可依据每个疏散个体的疏散时间估算出在此火灾场景下疏散运动时间的均值和方差，从而确定其分布情况。得到3个时间的分布后，利用蒙特卡洛法对整体疏散时间的分布进行求解。

按照蒙特卡洛法的学术思想，对分布情况进行随机取点，在此可随机取5 000个数据进行蒙特卡洛模拟，加和后可得到整体分布的数据，并依此作出整体分布的曲线。如图2和图3所示。

由此整体安全疏散时间-人员频数图可以推出在此火灾场景下预期死亡人数的求解公式:

3 提出预期死亡人数计算公式的意义

图2 蒙特卡洛模拟示意图

依据统计学理论分析火灾探测时间、预动作时间、疏散运动时间的分布规律，并据此通过蒙特卡洛模拟，从理论上解决了求整体安全疏散时间分布的问题。最后，通过整体安全疏散时间分布的统计学意义，与求解出的可用安全疏散时间联合，建立了确定场所在某特定火灾场景下的预期死亡人数的方法。用该方法预测的特定火灾场景下的预期死亡人数，虽然不能绝对性描述该建筑发生火灾时的实际死亡人数，但是该数据从统计学理论上描述了建筑物一旦发生火灾时的火灾风险大小，给建筑物和火灾高危场所的火灾风险定量评估提供了理论依据。

4 结论

图3 蒙特卡洛模拟结果示意图

本文通过分析火灾探测时间、预动作时间、疏散运动时间的不确定性及分布规律，借助蒙特卡洛模拟方法，从理论上解决了求整体安全疏散时间分布的问题。最后，通过整体安全疏散时间分布的统计学意义，建立了求解火灾场景下预期死亡人数n的方法。该方法考虑了从火灾发生开始后人员疏散的全过程，通过求解特定建筑火灾情况下整体安全疏散时间的分布，结合其他方法求解得到的火灾情况下可用安全疏散时间t0、安全疏散的开始时间t下限、安全疏散的结束时间t上限，根据整体疏散时间分布的统计学意义，定好3个时间点定积分可求得该建筑火灾情况下的预期死亡人数比例，结合安全疏散总人数可求得预期死亡人数。

［1］范维澄，孙金华，陆守香，等．火灾风险评估方法学［M］．北京：科学出版社，2004．

［2］HE Y P，WANG J，WU Z K，et al．Smoke Venting and Fire Safety in an Industrial Warehouse［J］．Fire Safety Journal，2002，(37)：191-215．

［3］褚冠全．基于火灾动力学与统计理论耦合的风险评估方法研究［D］．合肥：中国科学技术大学，2007．

［4］MAGNUSSON S E．Risk Assessment，Proceedings of the Fifth International Symposium on Fire Safety Science［C］//Ed．Hasemi Y．International Association of Fire Safety Science，Melbourne，1997：41-58．

［5］WANG H H，FAN W C．Progress and Programs of Fire Protection in China［J］．Fire Safety Journal，1997，(28)：191-205．

［6］RAMAEHANDRAN G．Extreme Value Theory and Large Fire Losses［J］．ASTIN Bulletin，1974，7(3)：293-310．

［7］汪金辉．建筑火灾环境下人员安全疏散不确定性研究［D］．合肥：中国科学技术大学，2006．

［8］张和平，亓延军，徐亮，等．可燃物表面积和厚度对建筑物内火灾载荷的影响［J］．火灾科学，2003，12(2)：90-94．

［9］British Standards Draft to Development DD 240，Fire Safety Engineering in Buildings，Part 1［S］．1997．

［10］HASOFER AM，BECK VR．Probability of Death in the Room of Fire Origin：an Engineering Formula［J］．Journal of Fire Protection Engineering，2000，10(4)：19-26．

［11］ FULIANG WANG，SHOUXIANG LU，CHANGHAI LI．Analysis of Fire Statistics of China Fire Frequency and Fatalities［C］//Fires Proceedings of the 8th International Symposium on Fire Safety Science．

［12］Fredrik．Tolerable Fire Risk Criteria for Hospitals［R］．Report 3101．Lund，Sweden：Department of Fire Safety Engineering，Lund University，1999．