竖直狭缝内泡沫材料火蔓延的数值模拟研究

●王 艳

(合肥市消防支队，安徽合肥 230001)

泡沫夹芯彩钢板是建筑和日常生活中常用的一种材料，火灾中泡沫材料的竖直火蔓延经常是造成火势变大和人员重大伤亡的重要原因，国外曾有不少学者做过关于狭缝内燃烧的研究［1-3］，吴振坤［4］等人研究了EPS彩钢板材的热释放速率特性和水平方向上的温度分布。黄新杰［5-6］等人试验研究了拉萨和合肥环境下不同厚度保温材料EPS的火蔓延特性。主要集中在小型的条形泡沫材料的火蔓延分析。而狭缝空间内泡沫材料的火蔓延由于其试验和测量分析的难度，相关研究还很少。因此泡沫材料在竖直狭缝中垂直方向的火蔓延速度的研究更具有重要意义。如2005年8月2日，安徽省马鞍山市某乳液有限公司冷库发生火灾，过火面积2 400 m2，直接财产损失361．53万元，3名消防战士在扑救火灾中牺牲。该冷库东西长82 m，南北宽32 m，为双层库体结构，内层为保温库，外层为维护库，中间间距1 m。火灾原因为照明电气线路短路引燃保温库墙体及顶棚泡沫夹心彩钢板，芯材内部的燃烧和热量的快速传播是火灾规模扩大并导致伤亡事故的主要原因。自2009年以来，安徽省共发生建筑工地夹芯板工棚火灾76起，造成直接财产损失160余万元。2011年4月12日下午，合肥百大电器五楼广告牌发生火灾，产生的烟雾很大，社会关注度极高。2011年7月12日，武汉经济技术开发区东荆路武汉东神轿车有限公司一出租仓库(EPS泡沫夹芯彩钢板)发生火灾，造成15人死亡。

1 数值模拟方法和场景设置

Fire Dynamic Simulator(FDS)是一款可以用于分析烟气蔓延和火蔓延的场模拟计算流体软件［7-8］。软件将务实的物理模型和高效的求解方法相结合，可以较精确的控制边界条件来分析多尺度空间结构下的火蔓延，能够计算分析泡沫材料宽度尺度较大，狭缝较小情况下的竖直火蔓延情况［9］。常见的小尺寸(如广告牌等)狭缝泡沫层火灾，一些大型墙体狭缝内的泡沫保温层火灾，往往泡沫层的横向宽度远远大于火源的尺寸，狭缝宽度一般远小于外部建筑板层的宽度和长度，所以其火源可以认为是线火源。

为了使分析更具有代表性，主要分析火源宽度为30cm，而泡沫保温层墙面宽度为4 m远远大于火源宽度的情况。关于火蔓延的分析主要基于壁面附近的温度分析，采用FDS技术模拟一个典型的外挂石材幕墙在外界高温辐射下发生引燃进而在夹板空隙间发生火蔓延的场景，通过对数值模拟结果的分析，研究火蔓延的特性和其羽流特性。图1为狭缝宽度为6cm计算结果的52．1 s时的火焰截图，其中狭缝的外金属板未显示。建立泡沫层宽度为4 m，高度为3．5 m的模型，对狭缝宽度为4cm、6cm、8cm三种情况进行模拟计算。在距离壁面1cm处截取不同时刻下5 s内的平均温度图，然后采用origin软件画出等温线图，选取500℃的等温线为火焰前锋线或者说是热解前端。图2为狭缝宽度8cm，时刻为80 s(代表80～85 s的平均温度)时的等温线和火焰前锋线的说明图。

图1 火焰截图

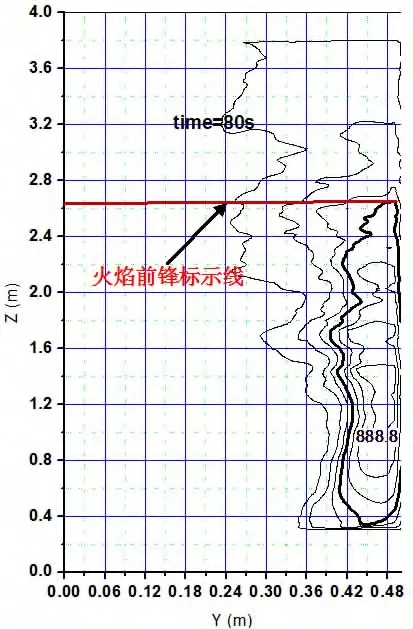
图2 等温线和火焰前锋线示意图

2 不同狭缝宽度下的火蔓延速度

Quintiere，Hasemi，Saito［10-14］等人在20 世纪80年代针对可燃材料的竖直火蔓延燃烧提出了一些火焰高度测量方法、分析模型和计算公式。其主要内容是通过热薄型假设和传热分析得出火蔓延速度公式(1)，然后在不同边界条件下求解此公式。

式中，Vp表示火蔓延速度;k为材料的热导率;ρ为材料的密度;c为比热;Tig为材料的点火温度;Ts为环境温度;xf为火焰高度;xp为热解区高度;qf为对材料表面的热辐射强度。式(1)可以较好的描述较窄的条形热薄型材料的火蔓延，但对本文中宽尺度下的火蔓延情况的适应性还有待检验。

表1、表2、表3分别给出了狭缝宽度为4cm、6cm、8cm下不同时刻的火焰高度、热释放速率和单位宽度热释放速率。其中单位宽度热释放速率=热释放速率/火源宽度。根据这些数据不但可以分析不同宽度下竖直火蔓延速度，同时也能分析出火焰高度和热释放速率间的关系，以及狭缝的空间结构对这些关系的影响。

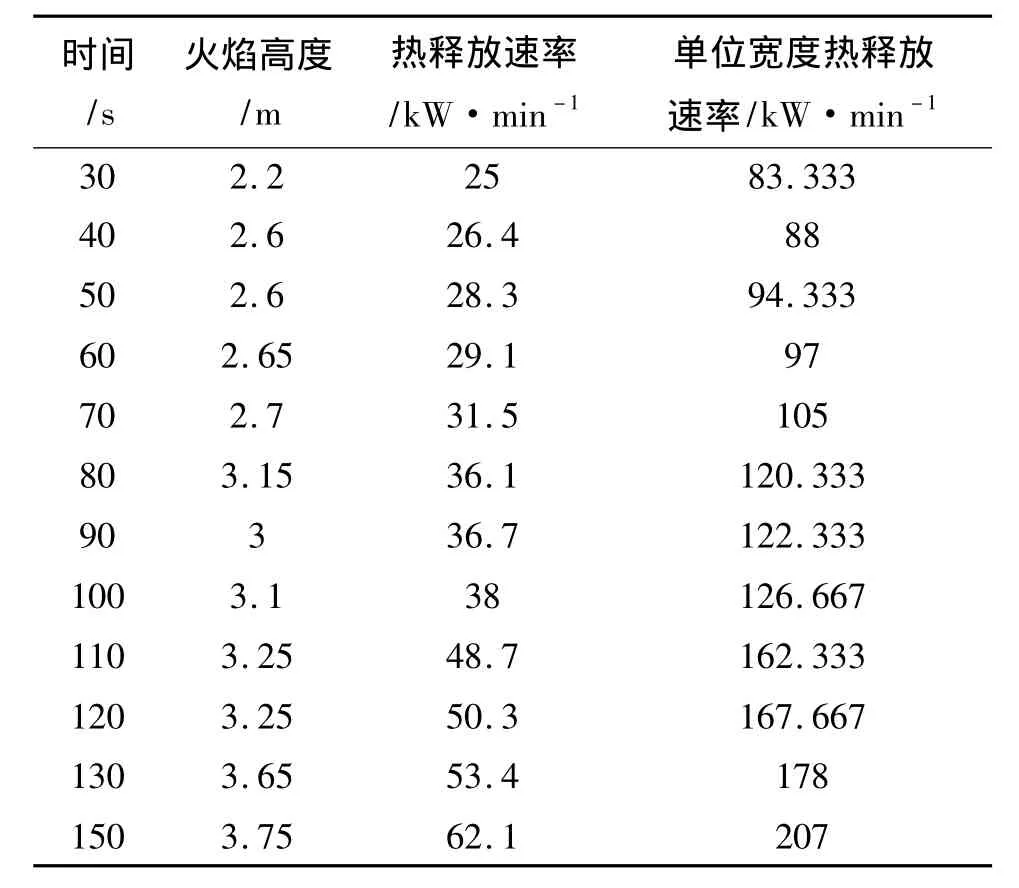
表1 狭缝宽度为4cm时的模拟数值

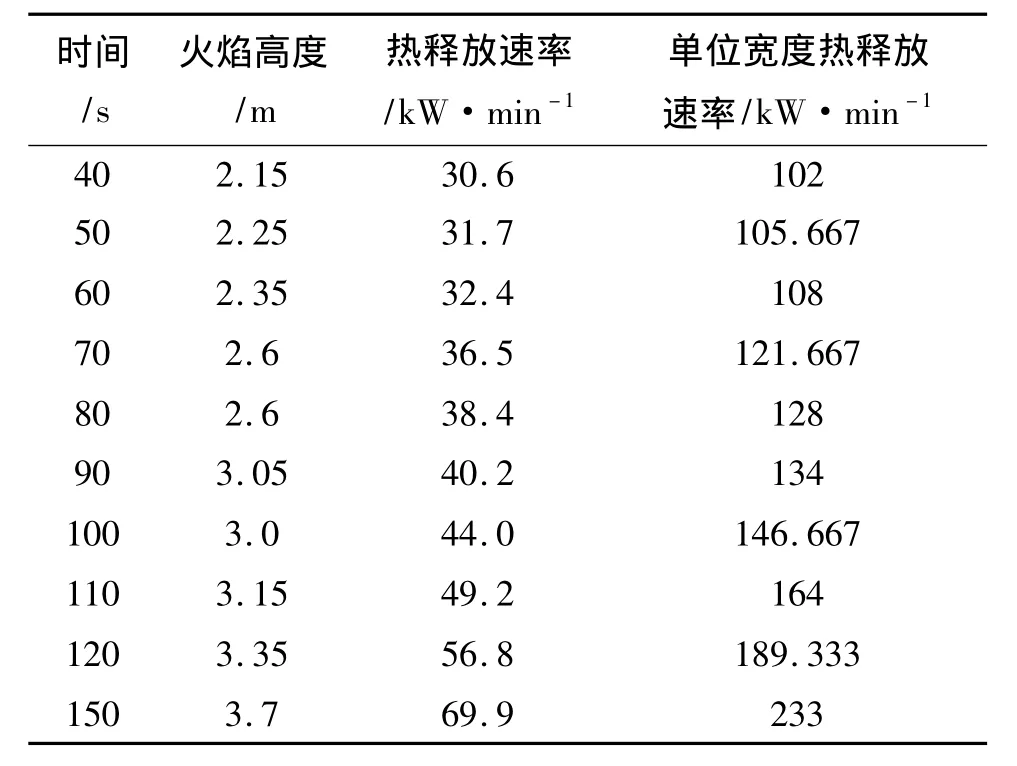
表2 狭缝宽度为6cm时的模拟数值

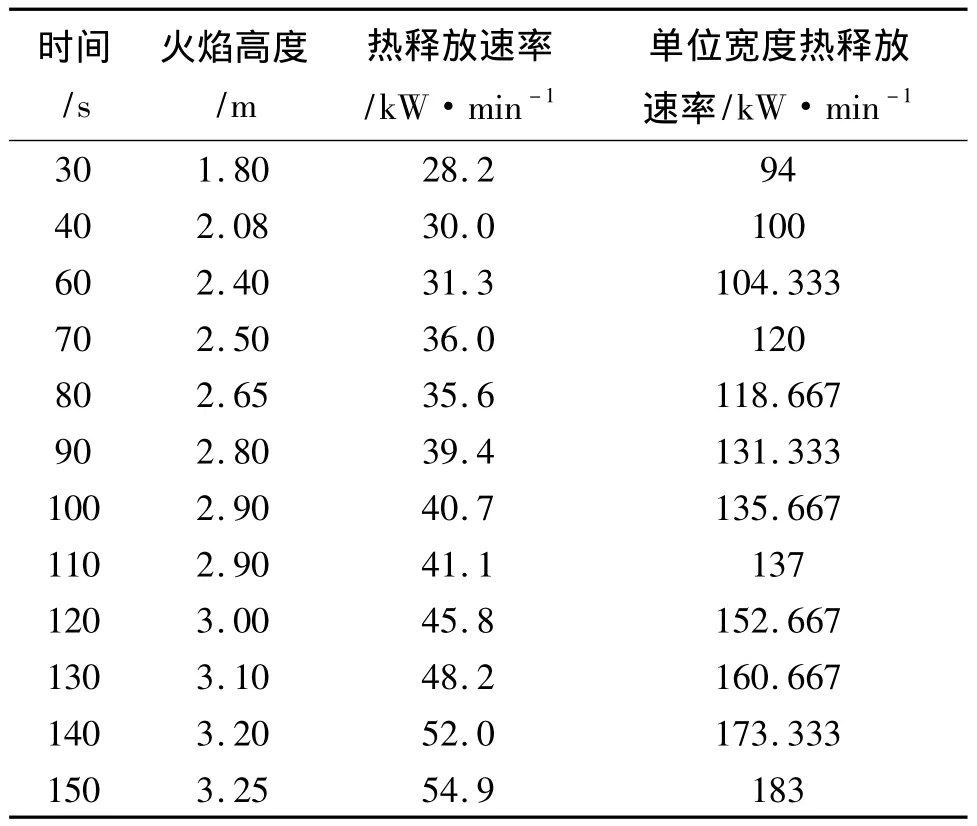
表3 狭缝宽度为8cm时的模拟数值

图3为狭缝宽度为4cm时的火焰高度随时间的变化。通过Origin软件对数据点进行线性拟合可以得出如下公式:

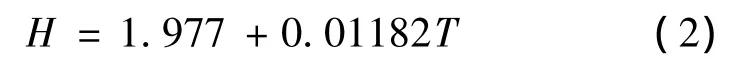
式中，H为火焰高度，T为时间。

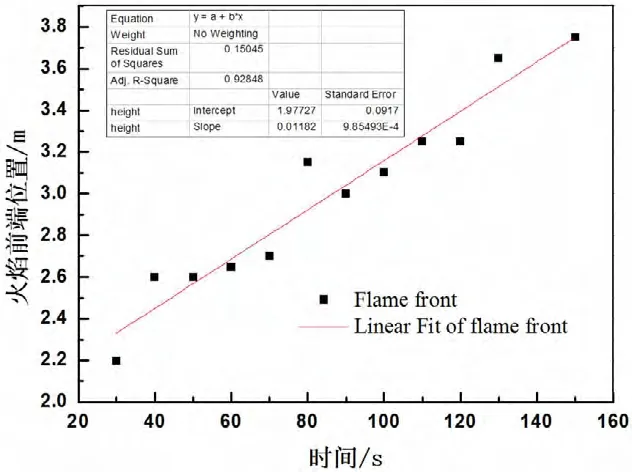
图3 狭缝宽度为4cm时火焰高度随时间变化图

即在狭缝宽度为4cm情况下其火灾初期竖直方向的火蔓延速度为0．011 82 m·s-1，即1．182cm·s-1。图4和图5分别为狭缝宽度6cm和8cm下的火焰高度随时间变化图，相同的拟合方式可以得出相应的关系式为:

式(3)和式(4)的斜率即为竖直火蔓延速度，狭缝宽度为6cm时的竖直火蔓延速度为0．014 13 m·s-1，即1．413cm·s-1;狭缝宽度为8cm时的竖直火蔓延速度为 0．011 4 m·s-1，即 1．14cm·s-1。

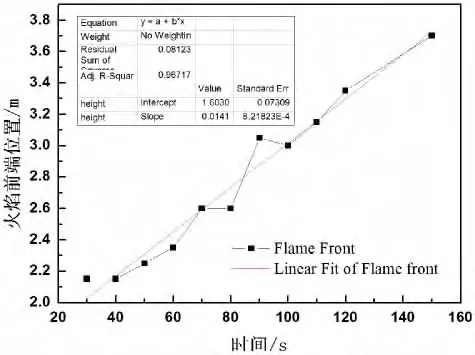
图4 狭缝宽度为6cm时火焰高度随时间变化图

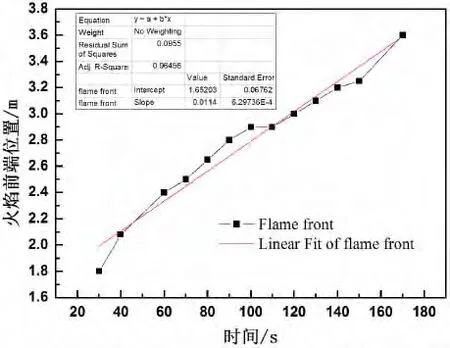
图5 狭缝宽度为8cm时火焰高度随时间变化图

显然，不同狭缝宽度下的火焰高度随时间变化的线性拟合公式可表示为H=a+bT。从公式中的数据分析可知:系数a的值在6cm和8cm下近似，而4cm下明显高于6cm和8cm的状况，可见在4cm情况下火焰更加细长，其初始火焰高度更大。竖直火蔓延速度在6cm时最大，而4cm和8cm下相接近。图6给出了不同狭缝宽度下的总热释放速率图，也可以看出在6cm情况下热释放速率最大。综合分析可得出:狭缝宽度在6cm时，由于涡旋作用增强，火蔓延速度和热释放速率均得到了增加，即在狭缝宽度为6cm左右时泡沫火灾在狭缝空间内的蔓延速度最快，其火灾发展也最快。

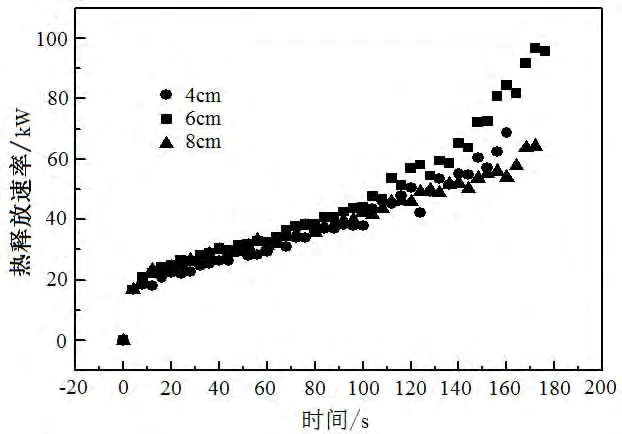
图6 不同狭缝宽度下的热释放速率曲线

3 火焰高度与单位宽度热释放速率的关系

Quintiere，Hasemi，Saito［10-14］等人在研究开放空间下，泡沫层等材料的宽度在5～30cm的情况下火蔓延特性，均发现泡沫等材料的竖直火焰高度与单位宽度的热释放速率存在一定正比关系，Delichatsios［15］的研究指出具体表达公式为:

式中，Qn为单位宽度的热释放速率，k为常数约等于4．6，n为常数约为 0．77。本文中研究的情况为，狭缝空间下并且材料宽度较大，而火源宽度为30cm左右的情况，这种情况和实际更为接近，但是其火焰高度和单位宽度热释放速率的关系更为复杂，和狭缝宽度甚至火源宽度都有关系。

由表1、表2和表3所列数据，通过Origin软件对火焰高度和单位宽度热释放速率进行了各种关系的拟合，最终发现两者的函数关系和式(5)最类似，但由于初始点燃火源的存在，拟合公式的单位宽度热释放速率项有一定的变化。其具体拟合公式如下:

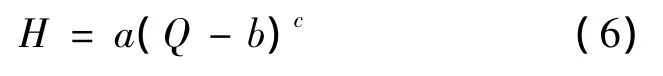
图7、图8和图9分别为Origin软件拟合的狭缝宽度为4cm、6cm和8cm时火焰高度与单位宽度热释放速率关系曲线图，并包含其误差分析。为了便于分析，表4列出三种情况下拟合公式的具体参数。

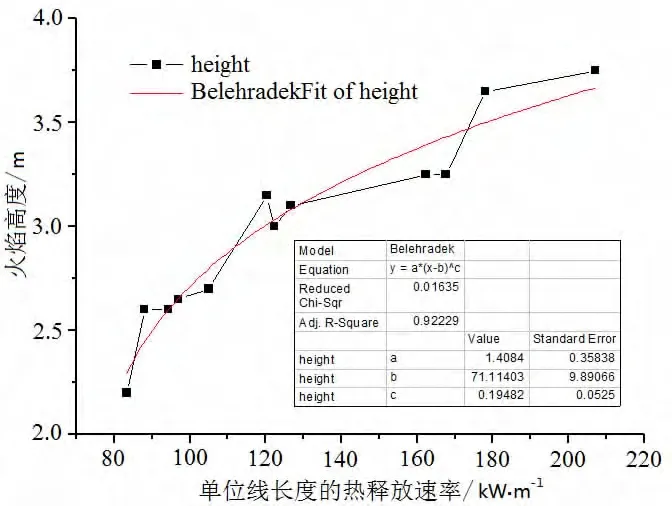
图7 狭缝宽度4cm时的拟合曲线

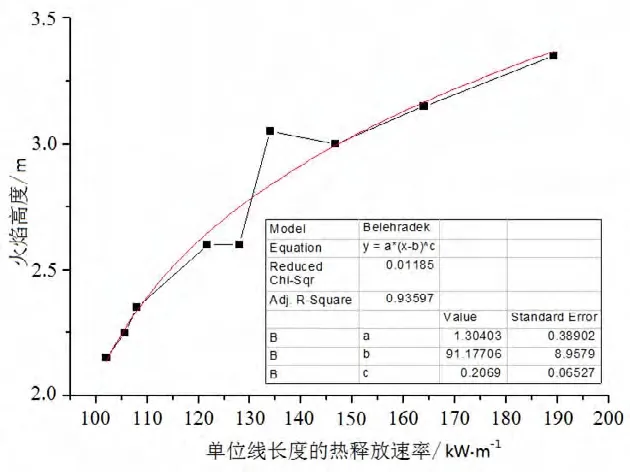
图8 狭缝宽度6cm时的拟合曲线

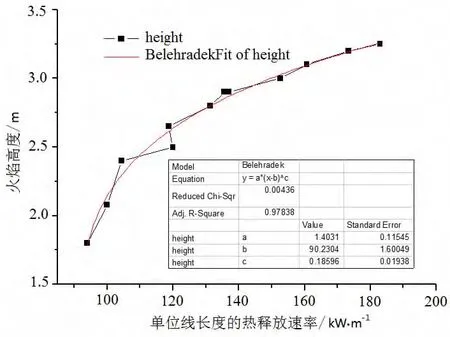
图9 狭缝宽度8cm时的拟合曲线

对比表4中的数据，可以得出以下结论:(1)从拟合公式的形式看，狭缝内较宽泡沫层的火焰高度和单位宽度的热释放速率的关系还是和前人的结论公式基本相符，均为幂次的函数关系，但是由于狭缝的作用和点火源的形式不同而存在一个单位宽度热释放速率校正的参数b。(2)从拟合公式的参数结果看，a和c在三种情况下相接近，均为1．4和0．19左右。系数b在4cm情况下比6cm和8cm略小，不过考虑到4cm情况下数据点震荡较大，相对误差较大，所以b的数值取90左右应该是合适的。(3)和Delichatsios的公式对比，a值约为k值的0．3倍，c值约为n值的0．24倍，即在狭缝内较宽的泡沫材料的火蔓延明显比开放空间下条状泡沫材料速度慢，这主要是受通风限制的影响造成的。

表4 火焰高度和单位宽度热释放速率拟合公式参数

4 结论

通过对现实案例中狭缝空间内泡沫墙面火蔓延的模拟分析发现，由于狭缝空间的特殊结构特点，其火蔓延速度和火焰形态与狭缝的宽度、泡沫层宽度等外界条件均有关。本文主要模拟研究了在泡沫层较宽的情况下的火蔓延速度。对大量模拟计算结果线性拟合得出了狭缝宽度4cm、6cm和8cm下的火焰高度随时间变化关系和火蔓延速度。竖直火蔓延速度在6cm时最大，而4cm和8cm情况下相接近。通过数据分析研究了单位宽度热释放速率和火焰高度的关系，并拟合得出公式H=a(Q－b)c，其中a约为1．4，b约为 90，c约为 0．19。从拟合公式的形式看，狭缝内较宽泡沫层的火焰高度和单位宽度的热释放速率的函数关系还是和前人的结论公式基本相符，均为幂次的函数关系，但是由于狭缝的作用和点火源的形式不同而存在一个单位宽度热释放速率校正参数b。和Delichatsios等人的计算公式H=kQn对比发现，由于通风受限，所以在狭缝空间下火焰高度随着单位宽度热释放速率的增加增长较慢，其中a值约为k值的0．3倍，c值约为n值的0．24倍。

［1］DR W TAYLOR．Fire Spread in Concealed Foamed Plastic Insulation［R］．National Research Council of Canada Division of Building Research:192-203．

［2］CXOI K K，TAYLOR K．Combustibility of Insulation in Cavity Walls［J］．Journal of Fire Sciences，1984，2(3):179-188．

［3］LIE T T．Contribution of Insulation in Cavity Walls to Propagation of Fire［R］．National Research Council of Canada Division of Building Research，1972．

［4］吴振坤，颜东升，尤飞．聚苯乙烯泡沫芯材的燃烧特性及其在火灾事故原因调查中的应用［J］．火灾科学，2007，16(3):180-184．

［5］黄新杰，孙金华，纪杰，等．不同外界环境下保温材料表面火蔓延规律研究［J］．科学通报，2010，55(32):3147-3152．

［6］黄新杰，纪杰，张英，等．拉萨和合肥环境下不同厚度保温材料EPS火蔓延特性研究［J］．灾害学，2010，25(S0):136-139．

［7］McGrattan K B．Fire Dynamics Simulator(Version 4)Technical Reference Guide［M］．National Institute of Standards and Technology，NISTIR，2006．

［8］YANG D，HU L H．Comparison of FDS Predictions by Different Combustion Models with Measured Data for Enclosure fires［J］．Fire Safety Journal，2010，45(5):298-313．

［9］范维澄，万跃鹏．流动及燃烧的模型与计算［M］．合肥:中国科学技术大学出版社，1992．

［10］RANGWALA A S，BUCKLEY S G，et al．Upward Flame Spread on a Vertically Oriented Fuel Surface:the Effect of Finite Width［Z］．Proceedings of the Combustion Institute 31，2007:2607-2615．

［11］QUINTIERE J G．The Application of Flame Spread Theory to Predict Material Performance［J］．Journal of Research of the National Bureau of Standards，1988，93(1):61-70．

［12］QUINTIERE J G，HARKLEROAD M．New Concepts for Measuring Flame Spread Properties［S］．NBSIR 84-2943，National Bureau of Standards(U．S．)，1984．

［13］QUINTIERE J G，HARKLEROAD M，HASEMI Y．Combust．Sci．Technol．［J］．1986，48．

［14］SAITO K，QUINTIERE J G，WILLIAMS F A．Upward Turbulent Flame Spread ［C］//Int．Association for Fire Safety Science，Fire Safety Science Proceedings，1st Int．Symposium．GRANT C E，PAGNI P J，Eds．，Gaithersburg，MD，Hemisphere Publishing Corp．，New York，1985:75．

［15］DELICHATSIOS M A．Flame Heights in Turbulent Wall Fires with Significant Flame Radiation ［J］．Combust．Sci．Technol．，1984，39．