基于FPGA实现的FFT速度与规模分析
2014-12-25刘智
刘 智
(佛山职业技术学院,广东 佛山 528137)
0 引言
FFT(快速傅里叶变换)是DFT 的快速算法,是把数据从时域到频域变换的基本运算.它是数字谱分析的必要前提,是数字信号处理的核心工具之一。现代数字信号处理是面向高速、大容量数据流的实时处理,其特点在于系统的输入、处理、和输出等各个处理阶段都具有绝对的时间限制。对实时性提出了很高的要求[1]。而FPGA 的高速并行结构,大量的内嵌RAM 和编程的灵活性,正好为FFT 的实现提供了一个平台。
现在已有多家FPGA 厂商提供FFT 的IP 核,但对其处理速度的研究,还只是停留在FFT 实现之后来观测所需要的时间,来确定其处理速度。没有一个可以在设计之前就具体估测处理速度的方式。这样就导致在用FPGA 设计FFT 时,面临达不到设计要求的风险。本文通过分析FPGA 实现FFT 的多种结构,研究分析了一个可计算不同结构、不同点数、不同主频下完成一次FFT 所用时间和所用乘法器个数的计算公式。通过这个公式,可以确定满足时间要求的FFT 的结构和确定芯片规模与型号的选取。并通过Altera 公司的软件进行验证。
1 蝶形算法结构分析
FFT 算法基本上分为两大类:一类是按时间抽取(DIT)的FFT 算法,另一类是按频率抽取(DIF)的FFT 算法。
首先,分析按时间抽取(DIT)的FFT 算法的结构。按时间抽样的基-2 的蝶形单元算法公式为[2]:

其中A、B 和Wp都为复数,完成一次运算需要1 次复数乘法。
按时间抽样的基-4 的蝶形单元算法公式为:[2]

其中A、B、C、D 和Wp、W2p、W3p都为复数,完成一次运算需要3次复数乘法。
由DFT 算法原理可知,对于按时间抽样其它基-r 的蝶形单元与基-2 和基-4 具有相同的规律。因此,设按时间抽样的其它基-r 的蝶形单元需要复数乘法次数为G1。则:

按频率抽样的基-2 的蝶形单元运算表达式为:[3]

其中A、B 和Wp 都为复数,完成一次运算需要1 次复数乘法。
按频率抽样的基-4 的蝶形单元运算表达式为:[3]


其中A、B、C、D 和Wp、W2p、W3p为复数,完成一次运算需要3 次复数乘法。
由DFT 算法原理可知,对于按频率抽样其它基-r 的蝶形单元与基-2 和基-4 具有相同的规律。因此,设按频率抽样基-r 的蝶形单元需要复数乘法次数为G2,则:
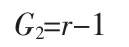
通过上面两个结论得到,无论是按时间抽取和按频率抽取的FFT,完成一个蝶形单元需要的复数乘法次数为:

设每个复数乘法器需要S 个实数乘法器来完成。根据高效复数乘法器的原理可知完成一个复数乘法,需要3 个实数乘法器[4],则S=3,而一般复数乘法需要四个实数乘法器,则S=4。FPGA 中内嵌的DSP乘法器为9 位,对于数据精度为M 位的FFT,每个实数乘法器需要个[M/9]DSP 乘法器来实现,(中括号表示向无穷大取整),令:
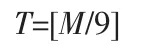
综上所述,不管是按时间抽样和按频率抽样,我们都能得到完成一个基-r 的蝶形单元需要的DSP 乘法器个数Q 为。
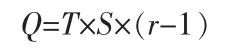
2 FFT 处理器的结构分析
根据FFT 算法的特点,硬件实现的结构基本可以分为四种:顺序型、级联型、并联型和阵列型四种结构。
在实际应用中确定FFT 的结构要考虑两点:(1)在考虑速度的前提下,要用内嵌的DSP 乘法器来完成乘法运算。同时FPGA 中的DSP乘法器个数有限,所以FFT 的结构都采用顺序型和并联型结合的方式。(2)在考虑输入点数N 可变的情况下,由于单独的采用一种基-r的方式,必须满足输入点数N 是r 的整数倍。
采用顺序型和并联型的方式,只需要运算一级所用到的蝶形单元,其它级都复用这些蝶形单元,节省了DSP 乘法器个数。对于r 个输入数据的基-r 蝶形单元又可以复用为2n个基-(r/2n) 的蝶形单元。例如,一个8 数据输入的基-8 的蝶形单元可复用为2 个4 数据输入基-4 的蝶形单元或4 个2 数据输入基-2 的蝶形单元。这样既节省了DSP乘法器个数,也可以满足输入点数可变的条件。同时采用流水线结构,这样保证在一个时钟周期内,所有的蝶形单元完成一次蝶形运算。在输入RAM 和输出RAM 之间进行数据的乒乓操作,减少了存储单元的消耗。
比较精度为M 位的N 点的FFT,其中N=2L,L 表示总级数。第i级采用基-ri 的蝶形算法,第i 级并联蝶形运算单元的个数为Fi。
其中i=1,2,…,logrN。
运算速度K 是计算一次FFT 所用的运算时间,对于顺序型和并联型,它们的每一级都要通过相同的蝶形单元计算,所用时间为L 个计算周期。即
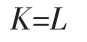
而级联型和阵列型是由多个蝶形单元同时计算,所用时间为1 个计算周期。即:

对于使用蝶形单元的个数:顺序型的特点是只有一个基-r 的蝶形单元,其中r=N,所有点都由一个蝶形单元顺序完成,即:

并联型的特点是有F=N/r 个基-r 的蝶形单元,每一级都用这F 个蝶形单元运算。即:

级联型和阵列型的特点是每一级都采用独自的蝶形单元,所以它们使用的蝶形单元是顺序型和并联型的r 倍,而速度也是顺序型和并联型的r 倍,只有一个运算周期。
综上所述,对于不同结构,只要已知每一级不同基的蝶形单元的个数,就能计算出FFT 处理器总共的蝶形单元的个数U。
计算公式为:

取精度M=18 位的N=16 点FFT,其中每个复数乘法需要实数乘法的个数S=3,通过不同结构在FPGA 上实现可得到下表的结论:

表1 不同结构下乘法器的使用数量和运算速度表Tab.1 The use of different structure by multiplier quantity and speed
3 FPGA 最高频率分析
如图1,FPGA 中计算最小时钟周期公式为[5]:

图1 寄存器传送图Fig1 Register transfer

式中:tclk为时钟的最小周期;
Microtco为寄存器固有时钟输出延时;
tlogic为同步元件之间的组合逻辑延迟;
tnet为网线延迟;
Microtsu为寄存器固有时钟建立延时;
tclkskew为时钟偏斜。
FPGA 运行的最高频率为最小时钟周期的倒数。

基于FPGA 的FFT 算法实现时,FPGA 的最高频率限制在乘法器输入输出寄存器之间,而tclk 主要有tlogic 和tnet 决定。所以在FPGA实现FFT 算法的时候,每执行一次乘法运算最高频率为:
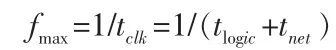
也就是执行一个运算周期的频率。
所以执行一次FFT 的最高频率为:

4 验证
式(1)和式(2)分别为完成FFT 运算需要的乘法器数量计算公式和最高频率计算公式。根据Quartus 软件是Altera 公司推出的一款专门针对Altera 的FPGA 程序设计的一款软件。Quartus 自带FFT 的IP核,通过对比IP 核提供的乘法器使用数据,可以验证本研究的计算公式的准确性。下表是Altera 的并联型FFT 的IP 核的乘法器使用数量的对比。

表2 公式计算和Quartus 数据结果对比表Tab.2 The formula to calculate and parameter of Quaruts contrast table
5 结论
通过研究快速傅里叶变换在FPGA 中的实现,研究总结了一条经验公式来计算需要用到的乘法器个数,以及运算速度问题。但对于大规模的FPGA 程序,不同的综合工具,综合得到的最高运行频率会有不同。通过此公式可以为设计FFT 提供参考。
[1]高瞻.FFT 处理器设计及其应用研究[D].西南交通大学,2006.
[2]白德风.基于FPGA 的FFT 信号处理器的设计与实现[D].北京工业大学,2008.
[3]张竺君.基于FPGA 的可变点FFT 处理器的设计与实现[D].南京理工大学,2009.
[4]刘凌.数字信号处理的FPGA 实现[M].清华大学出版社,2008.
[5]吴继华,王诚.Altera FPGA/CPLD 设计(高级篇)[M].人民邮电出版社,2005.
