一种基于ECC的Ad hoc 网组密钥协商协议
2014-12-24向婉芹陈乙源
向婉芹,陈乙源,李 燕
(重庆电力高等专科学校,重庆400050)
Ad hoc网络是一种特殊的无线移动网络[1]。该网络中所有节点地位平等,无需设置任何中心控制节点,是一种动态对等网络(Dynamic Peer Group,DPG),其研究方法和实施方案都与传统网络有巨大的差别。Ad hoc网络中,每个节点同时担当终端和路由器的角色,当两个通信节点在一跳(hop)范围内,可以直接通信;否则,由其他节点作为路由器中继转发它们的通信。节点可以随时加入或离开网络,任何节点的故障不会影响整个网络的运行。Ad hoc网络具有很强的抗毁性,并且可以快速自动组网,在抢险救灾中具有极大的价值。目前对Ad hoc网络研究的一个热点问题就是如何制定安全高效的组密钥协商协议[2]。
本文利用椭圆曲线密码体制,结合密钥生成树的思想,提出了一个基于ECC的Ad hoc网组密钥协商协议。该协议结合Ad hoc网络的拓扑结构,通过密钥协商建立并维护虚拟密钥树,为动态变化的Ad hoc网络组成员之间的保密通信提供了一种有效的密钥协商机制。
1 椭圆曲线密码体制
1.1 椭圆曲线密码体制
椭圆曲线密码体制(Elliptic Curve Cryptography)[3]是近些年发展起来的一套新的密码机制,可以描述如下:
定义E(a,b):y2=x3+ax+b为一椭圆曲线,考虑等式K=kG。式中,K,G为E(a,b)上的点,k(k<n,n为点G的阶)的整数。
根据密码学理论,给定k和G,利用椭圆曲线的加密法则,计算K很容易;但给定K和G,求k就相对困难了,这就是椭圆曲线加密算法采用的难题。其中,G点称为基点(base point);k(k<n)称为私有密码(private key);K称为公开密钥(public key)。
1.2 椭圆曲线密码体制的安全强度
公钥密码的安全性建立在数学难题的难解性上[4]。一类是一般群上的离散对数问题(DLP);另一类是椭圆曲线上的离散对数问题(ECDLP)。ECDLP是在已知椭圆曲线离散群中一点P和nP后,攻击者无法获得n。在同等安全强度要求下,ECDLP所需要的密钥长度要低得多(见表1)。从表1可看出,采用椭圆曲线密码的密码体制具有较高的实现效率。

表1 同等安全强度下密钥位长度比较
2 密钥协商描述符号
2.1 密钥树编码[5]
本文使用的密钥树为二叉树[6],密钥树中第l层第m个节点 V记为 <l,m >;根节点 R记为<0,0>。如果V是非叶子节点,则它有且只有一个左子节点 <l+1,2m>和一个右子节点 <l+1,2m+1 > 。每个节点 <l,m > 有一个密钥K<l,m>和一个私钥 BK<l,m>。

式中,f(k)=αkmodp;α为设备固化值。
密钥树中每个叶子节点V:<l,m >对应一个Ad hoc 网络成员 Mi,并且 K<l,m>即为 Mi的会话密钥。从节点V到根节点R的路径上的所有节点(包括R)形成Mi的密钥路径PKi。PKi中所有节点的密钥和私钥分别为K*i和。K*i中每个节点(不含R)的兄弟节点的隐蔽密钥形成Mi的协同隐蔽密钥。
非叶子节点 <l,m >的密钥可以由其子节点的密钥和私钥协商生成,计算公式为

由于所有成员的密钥路径中都有 K<0,0>,因此,组通信密钥KG为

式中,h(x)为强哈希函数。
综上,Mi通过存储并维护 PKi、K*i、BK*i和CK*i,即可得到组通信密钥KG;每个成员最多保存并维护密钥树的h个节点(密钥树高h),成员记录的信息综合即构成一虚拟密钥树,如图1(a)所示。

图1 网路拓扑结构与密钥树
2.2 密钥树的建立
假设网络拓扑如图1(a)所示,所有成员节点可以知道它们的一跳邻居节点。本协议中,任意节点均可以发起密钥协商操作,发起节点记为S。S向所有邻居节点发出协议发起信息,节点在收到信息后,给出回应,S挑选最早回应的节点P组加入密钥树,并向P发出回应信息。S响应其他回应的邻居节点。P向其邻居发出密钥树建立信息,并将回应的邻居节点加入密钥树。直到所有成员都加入密钥树,结果如图1(b)所示。
如果一个节点收到多余一条协议发起信息,则选择第一个作为回应,其余不予响应。如果节点发出信息后,没有邻居节点回应,则称其为密钥树的叶节点。
2.3 最左密钥路径
设 <l,m >∈PKi,且 <l,m > 为非叶子节点,若令,且l' > l、m'为偶数,则L<l,m>为相对于 <l,m'> 的最左密钥路径。
利用满二叉树的相关理论,不难证明,每个非叶子节点的最左密钥路径有且只有一条[5]。
3 密钥协商协议
3.1 密钥协商初始化
Step1:设置系统参数 (E(a,b),α,p),并依照网络拓扑结构,建立密钥树。
Step2:密钥树中每个叶子节点 Mi随机产生xi∈Zp作为密钥Ki,并计算其私钥,记为BKi。
Step3:叶子节点Mi将Ki、BKi发送给自己的兄弟节点Mr,并计算共同父节点Mv的密钥。并将协商的结果进行广播。
Step4:叶子节点Mi根据其他叶子的协商结果,对密钥路径PKi上的所有非叶子节点的密钥进行计算和维护。
3.2 成员加入
如果Mj欲加入网络,首先向自己属于该网络的邻居节点Mi发送加入请求,Mi收到请求后对此作出反应。为了确保网络的安全性,Mj与Mi应进行相互认证,待认证通过后,Mi“推荐”Mj加入网络,并同时广播密钥树更新信息。成员加入的过程如图2所示。

图2 网络成员加入过程
Step1:Mj随机生成Kj和BKj,向Mi发出加入申请,双方交换公钥。
Step2:Mi将自己的密钥加密发送给Mj,Mi→
Step3:Mj接到Mi的消息后,解码得到BKi。利用Kj和BKi计算出二者协商密码Kji,并Mj→Mi:
Step4:Mi接受到Mj消息后,通过解码的到BKj和EKji(BKi)。利用Ki和BKj计算出二者协商密码K'ji,进而得 BK'j=DK'ji(EKji(BKj)),如果 BKj=BK'j,则认证成功,否则失败。认证成功时,如果Mi无兄弟节点,则Mj成为Mi的兄弟节点;否则,密钥树中生成一新节点取代Mi的位置,而Mj和Mi都成为该新增节点的子节点,并将Mi和Mj协商的密钥作为该节点的密钥。
Step5:Mi修改K*i中的 K<l,m>=Kji,且 Mi→
Step6:Mj收到Mi的消息后,生成自己的密钥树信息。
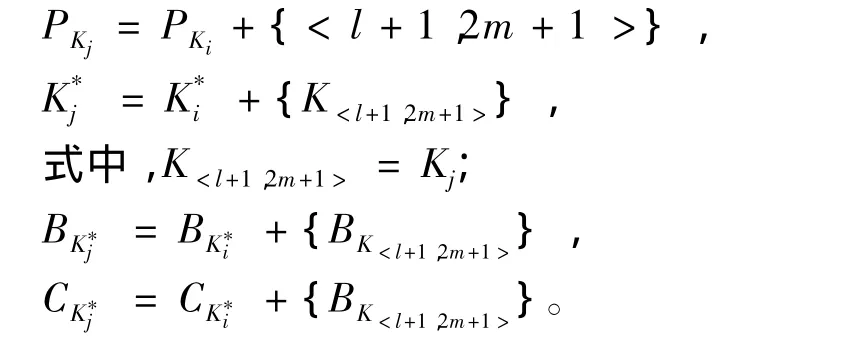
Step7:Mi修改自己的密钥树信息。

Step8:Mi广播密钥树的变化,Mi和Mj所在的密钥树路径上的节点对密钥进行维护和更新。
设定网络中每个组成员(包括已加入和未加入的)彼此知道对方的公钥Ki,pub,而其私钥Ki,pri则完全保密。
3.3 成员退出
成员离开过程图3所示。
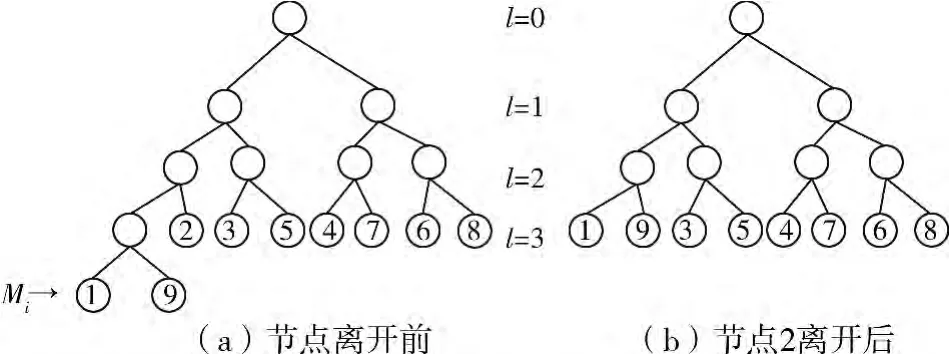
图3 网络成员退出过程
任一叶子节点 <l,m >上成员Mi离开,有两种情况:
1)叶子节点离开后,其父节点还有其他的叶子节点,如图3a中节点1的退出。此时,其父节点的子节点为非满,故删除其父节点,其兄弟节点替代其父节点的位置,并更新密钥树。
2)叶子节点离开后,其父节点没有其它的叶子节点,如图3a中节点2的退出。此时,其父节点的子节点为非满,故删除其父节点,其兄弟节点替代其父节点的位置,并更新密钥树。
无论节点是主动离开还是被动离开,均可用相同的方式更新维护密钥树。
4 协议安全性分析
(1)安全保密性。本协议的安全性是建立在椭圆曲线密码体制之上的,对于被动对手而言,要攻破密码必须破解椭圆曲线上的离散对数难解问题,因此协议实现了密钥的安全保密性。
(2)前向安全性。当有新的成员加入时,其所在的密钥路径上的所有节点的密钥均重新协商,故无法获得旧的组密钥,因而协议实现了前向安全性。
(3)后向安全性。当旧成员离开后,其所在的密钥路径上的所有节点也发生了密钥协商,故无法获得新的组密钥,因而协议实现了后向安全性。
(4)密钥独立性。当有成员变化时,组通信密钥KG均会重新计算,且与旧值无关,因此实现了密钥的独立性。
5 结语
本文主要研究了在Ad hoc网络中的行密钥协商协议,结合椭圆密码体制和密钥树的思想,提出一个密钥协商协议,为动态变化的Ad hoc网络组成员之间的保密通信建立了一种有效的密钥协商机制。该协议具有节点加入认证功能,并对节点的动态退出提供了良好的支持。
[1] 郑少仁,王海涛,赵志峰,等.Ad hoc网络技术[M].北京:人民邮电出版社,2005.
[2] 王昌达,鞠时光.无线自组网技术中的安全问题[J].计算机科学,2006,(7):121-124.
[3] 徐永道,高振明,王美琴,等.移动Ad hoc网络基于椭圆曲线密码体制的安全性研究[J].山东大学学报(理学版),2004,(4):71-76。
[4] Stinson D R.密码学原理与实践[M].北京:电子工业出版社,2009.
[5] 何聚厚,李伟华.对等组内安全通信密钥协商协议[J].西北工业大学学报,2003,(4):406-409.
[6] 霍罗威茨.数据结构(C语言版)[M].北京:机械工业出版社,2006.
