基于拓扑排序的部队输送序列问题研究
2014-12-24吴晓东朱桐生
吴晓东,杨 斌,朱桐生
(1.军事交通学院 联合投送系,天津300161;2.军事交通学院 研究生管理大队,天津300161;
3.驻郑州铁路局军事代表办事处,郑州450000)
输送序列是指部队输送的先后顺序。大规模部队输送应优先考虑输送序列,只有按照输送序列组织,尽量压缩输送持续时间,以确保在规定的输送期限内完成输送任务。不顾输送序列,片面提高输送进度,追求快速反应能力和应急机动能力,可能会打乱整个战役部署,破坏作战企图的实现,造成严重后果。因此,确定部队的输送序列是进行部队输送的首要工作,按照输送序列实施输送是输送组织的严格要求。本文通过建立序列树模型以描述部队输送序列要求,设计相应的拓扑排序算法。
1 模型描述
多个部队组成的集合A= (a1,a2,…,an)中,部队的重要程度不尽相同。据此要求某些部队在输送中满足特定的先后关系,但并不是所有的部队在输送中的先后关系都是明确的。如:有的部队全体要求比另一部队都提前到达;有的部队要求有下属部队比另一部队的下属部队提前到达;有的部队相互间没有关系。发现集合A是一个偏序集,即有如下定义。
(1)设L为一集合,x,y,z∈L,L的一个偏序是一个二元关系R,满足:①xRx(自反性);②xRy∧yRx⇒x=y(反对称性);③xRy∧yRz⇒xRz(传递性)。
具有偏序关系R的集合L称为偏序集[1],记为(L,R)。如果对每个x,y∈L,必有xRy或yRx,则称R是集合上的全序关系。由某个集合上的一个偏序加强为该集合上的一个全序,这个操作称为拓扑排序。可以用无圈图表示一个偏序集,每个节点表示一个元素。如将无圈图G中的所有顶点排成一个线性序列,使得图G中任意一对顶点u和v,若(u,y)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序的序列,简称拓扑序列[2]。对于部队输送而言,简单的偏序关系还不能完全描述序列要求,本文再进行如下定义。
(2)树:无圈的连通图称为树(又称树图,记作T(V,E))。
(3)绝对优先关系:树中∀非父子的2 个节点a、b,如果a比b重要(a』b),且a的任一子节点都比b的任意子节点重要,称a﹥b。反之,如果a没有b重要(a『b),且a的任一子节点都没有b的任意子节点重要,称a﹤b。如果a与b重要程度相同,称a≒b。这3 种关系统称为2 个节点具有绝对优先关系。
(4)相对优先关系:树中∀非父子的2 个节点a、b,如果a存在某一子节点比b和b的任意子节点重要,称a』b。反之,如果a存在某一子节点没有b和b的任意子节点重要,称a『b。这2 种关系统称为2 个节点具有相对优先关系。
(5)节点相关性与无关性:具有绝对优先关系和相对优先关系的2 个节点称为具有节点相关性,或2 个节点有相互关系。如果a与b重要程度没有可比性,且a的任意子节点与b的任意子节点的重要程度都没有可比性,称2 个节点具备节点无关性,或称2 个节点没有相互关系,记为a><b。
(6)序列树:∀非父子的2 个节点间存在节点相关性或者节点无关性关系的树称为序列树。序列树有如下性质。
①序列树中的2 点a、b,如果a﹥b,则a中任一子节点a’与b中任意子节点b’都有关系a’﹥b’,且有a』b。如果a﹤b,则a中任一子节点a’与b中任意子节点b’都有关系a’﹤b’,且有a『b。
②序列树中的3 点a、b、c,如果存在a﹥b,b﹥c,必然存在a﹥c。同理,如果存在a﹤b,b﹤c,必然存在a﹤c。如果存在a』b和b』c,必然存在a』c。同理,如果存在a『b和b『c,必然存在a『c。
③D=(d1,d2,…,dn),S=(s1,s2,…,sn)是序列树的中的点组成的2 个集合,如果有D<S,则有D中的任一di﹤S中的任一sj。如果有D>S,则有D中的任一di>S中的任一sj。如果有D><S,则有D中的任一di><S中的任一sj。
根据以上定义,整个部队输送序列问题可以用序列树来表示,每支部队可以用节点来表示,部队的隶属关系可以用节点的父子关系表示,部队输送序列可以用节点间的相关关系表示。
2 决策树算法
对于拓扑排序已经有的方法[3-5],拓扑排序的算法思想通常描如下。
(1)在AOV 网中选一个没有前趋的顶点且输出。
(2)在网中删去该顶点及其所发出的弧。
(3)重复(1)、(2),直至输出全部没有前趋的顶点。
当过程结束时,如果网中的所有顶点均已输出,则说明网中不存在回路,否则说明网中存在回路,相应的排序是不可行的。
考察输送序列问题,根据上文所述依据与原则,可定性比较部队间的重要程度,并能够确定其中某些部队的相互关系。但由于定性描述的局限性,难以明确所有部队的相互关系,也就无法确定所有部队的序列。AOV 网的排序方法虽然可以很好地表示顶点的相互关系,但是无法描述部队的上下级层次隶属关系,也难以表示部队的不同方向与不同任务。考虑部队的上下隶属关系与“树”的某些特性非常相似,通过树的父子节点关系可以很好地描述部队的上下级隶属关系以及运输中分方向、分属性等特性。本文将输送部队建成一个分层的权重树,一个部队对应一个节点,父子节点代表上下级单位,通过对树节点的依次搜索,实现对节点排序,从而实现运输序列排定。算法思路如下:通过建立节点关系表、节点初始权重赋值、节点搜索排序3 个步骤实现。首先建立节点关系表,对既有节点关系进行分析与推理,然后通过一定算法对节点赋权重值,最后通过搜索确定节点的序列。
2.1 建立节点关系表
将节点间的关系用列表的方式完整的表达出来,称该列表为节点关系表。建立节点关系表步骤如下。
(1)初始节点关系的确立。一是直接对节点关系的指定,即根据第一部分模型描述定义(4)、(5)确立;二是通过节点属性及属性间的优先关系间接的指定,即依据序列树的性质确立,这一步骤不明确,难以操作。
(2)为节点关系划分优先等级。根据节点关系的重要程度,可为节点关系明确优先等级。可将所有的节点关系划分为若干等级,等级低的关系服从于等级高的关系,其目的是为了节点关系出现冲突时进行疏解,要有明确的划分方法。
(3)节点关系冲突的疏解。在多个节点关系中,有时会出现相互冲突。比如出现a>b,b>c,c>a,这时就需要对冲突进行疏解。在发生冲突的关系间,必须首先划分各自得优先等级,然后依据低等级关系服从于高等级关系的原则,在节点关系表中将冲突中等级低的关系删除,最终得到没有冲突的节点关系表。冲突种类可划分为2 类:①对向冲突。即经过推理,2 个节点间出现对立的相互关系。即经过推理得到a>b,同时b>a或b『a,例如由a>b,b>c,c>a可得,或者a<b,同时b<a或a』b;②无关性冲突。即经过推理,2个节点间出现既无关又相关的2 种关系。例如,经过推理得到a>b或b>a,同时b><a。
2.2 节点初始权重赋值
节点初始权重赋值思路如下:将所有的节点依据权重等级分层,同等级的节点权重相同,等级高的层级权重高于等级低的权重。每次迭代寻找重要程度最低的若干节点,将这些节点放入当前的最低权重等级,其权重即为当前层次的权重。本次迭代完毕后,将最低权重等级的所有节点从序列树中去除,设立新的层次与权重,用同样方法搜索并赋权,直到所有的节点赋权完毕。算法步骤如下。
(1)令k=1,权重系数c≥1。所有节点集合S=(s1,s2,…,sn),节点数为n,叶子集合D=(d1,d2,…,dm)。叶子数为m。显然有D∈S。
(2)标记向量B=[0,0,…,0]m。
(3)S中节点与叶子di相比较(考察节点关系表),如果存在某一节点sw>di,且不存在任意节点sv使得di>sv,则标记向量bi=1。
(4)i=i+1;如果i>m,步入(5),否则回到步骤(3)。
(5)bi=1(i=1,2,…,m)的节点为标记节点。标记节点的权重fi=fi+c·k。从S和D中除去标记节点,得到新的节点数n’和叶子数m,更新节点关系表。如果n’>0 且n>n’,则n=n’,m=m’,k=k+1,回到步骤(2),否则,所有未赋值节点权重fi=fi+c·k,计算完毕,退出。
这一方法优点是通过分层可以清晰、完整地表达任意两节点间的绝对优先关系,但是这一方法的局限性是不能有效表达相对优先关系。相对优先关系将在下文的搜索方法中体现。
2.3 节点搜索排序
在介绍方法之前引入2 个定义。
(1)节点信息熵。在序列树中,任一节点所包含的叶节点数目为m,搜索过程中的任一时刻,未曾搜索的叶节点数为n。若该节点为非叶节点,即m>0,则节点的搜索信息熵ω=(n-1)/m;如果该节点为叶节点,即m=0,则节点的搜索信息熵ω=1。节点的搜索信息熵简称节点信息熵。
(2)节点链。在序列树中,从根节点b经由各中间节点(n1,n2,…,nm),至某一叶节点y组成的链表称为该叶节点的节点链,即节点向量Ny=(b,n1,n2,…,nm,y)。
节点搜索排序的原则:任意父节点在其所有子节点选取完毕后方可选取(因为父节点是子节点的总和,在采取结束验证序列方法下,子节点不搜索完毕,父节点不能算搜索完毕);选取节点时,要尽量保证同等重要的节点具有相同的搜索几率,并保证能够几乎同时完成搜索(在部队输送中,可保证若干相同重要程度的部队齐头并进,通过并行机制,能够为最快时间完成输送创造条件)。依据节点搜索排序的原则,设计搜索算法分为以下2 步骤。
2.3.1 建立权重分层序列树
依据权重由高到低将所有节点分为若干权重层。同一层次的节点具有相同的权重值,即同层次的任意节点的重要程度相当。依据权重层次,可建立权重分层序列树。
2.3.2 搜索权重分层序列树
本文提出依据节点搜索信息熵进行权重分层序列树搜索的算法。由于搜索的原则是力求等同重要的节点具有同等的搜索几率,因此同等重要节点的子节点(尤其是叶节点)应具有同等搜索几率,搜索信息熵正是反映这一信息。通过下一步节点搜索的概率信息,搜索时选择搜索信息熵最大的节点,可以保证各等同重要节点的尽可能同时完成搜索。搜索权重分层序列树的思路如下。
(1)依据层次的高低先后搜索。
(2)在每一层搜索时,考察该层所有的叶节点的节点链,则所有叶节点的节点向量组成了一个节点矩阵。考察矩阵的每一行,比较其中每一节点的搜索信息熵,选择最大者。如果信息熵最高的节点有多个,选择叶节点数少的节点;如果叶节点数最少的节点也有若干个,通过平均概率选择其中某一节点。如果选中的某一节点出现在若干节点向量中,向下考察下一行,同样方法搜索新的节点,直到搜索到叶节点。
(3)在对节点矩阵的每一行比较时,考虑节点的相对优先关系。为每行的节点分层(分层方法同上),首先为节点赋权重,再依据权重分层(同权重分层序列树方法)。具有较高相对优先关系的节点的层次高于具有较低相对优先关系的节点。依据分层进行节点的搜索,先搜索具有高层次的节点,后搜索低层次的节点。可以看到,当某节点的某一子节点搜索完毕后,其相对较高的优先关系取消,节点放入下一层次。同理易见,任一节点的相对较低优先关系直到其所有子节点搜索完毕后才取消。同层次的节点搜索方法同思路(2),优先选择信息熵最大的节点。
权重分层序列树搜索的步骤如下:①设定搜索的层次。令m=1,从最高层开始搜索。②考察m层所有的叶节点,如果叶节点为空,m=m+1,回到②。建立由节点链组成的节点矩阵Nm。设定Nm搜索的行向量Nm(j),令j=1,即从第1 行(根节点)开始搜索。③依据相对先后关系为j行向量节点赋权重。④依据权重为j行向量节点分子层。同等权重的节点为同一子层,权重高的节点层次高于权重低的节点。搜索j行向量,如果考察对象向量Nm‘(j)没有赋值,令j行向量中所有的节点组成考察对象向量Nm‘(j)。⑤研究j行向量中的考察对象向量Nm‘(j),选择最高子层作为研究对象。比较该层所有节点的信息熵,选择最大的若干节点,形成j+ 1 层的考察对象向量Nm‘(j+1)。如果Nm‘(j+1)中包含叶节点,进入⑥,否则,令j=j+1,回到③。⑥通过平均概率选择Nm‘(j+1)中包含的叶节点的一个,将该节点存入搜索结果列表,序列树中删除该节点,更改其节点链中其他节点信息熵。如果某父节点不存在其他子节点,将该父节点存入搜索结果列表,序列树中删除该节点,同时更改节点链其他节点的信息熵。此时,如果序列树中节点已全部删除,计算完毕,退出;否则,m=m+1,进入②。
其中,步骤③中依据相对先后关系为j行向量节点赋权重的方法如下:ⓐ令k=1,权重系数c≥1,节点行向量的节点集合S=(s1,s2,…,sn),节点数为n;ⓑ标记向量B=[0,0,…,0]n;ⓒS中节点di与其他节点相比较(考察节点关系表),如果存在某一节点sw』di,且不存在任意节点sv使得di』sv,则标记向量bi=1;ⓓi=i+1,如果i>n,步入ⓔ,否则回到ⓒ;ⓔbi=1(i=1,2,…,n)的节点为标记节点。标记节点的权重fi=fi+c·k。从S中除去标记节点,得到新的节点数n’,更新节点关系表。如果n’>0 且n>n’,则n=n’,k=k+1,回到ⓑ,否则,所有未赋值节点权重fi=fi+c·k,计算完毕。
3 算 例
如图1 序列树中,存在节点间关系:节点2 >节点3,节点32 >节点22,节点31 >节点33,节点33 >节点42,节点31 >节点43,节点41 >节点21。其中:关系节点2 >节点3 最为重要,求解决策树的节点排序;节点2、节点3、节点4 分别指3个部队,其下属节点分别为这些部队的下属单位。节点排序即表示部队的输送序列。
3.1 建立节点关系表
(1)初始节点关系表。建立初始节点关系表,其中,由于s2>s3,将s2与s3的子节点间关系明确(见表1)。
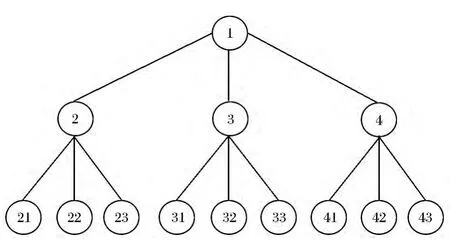
图1 序列树
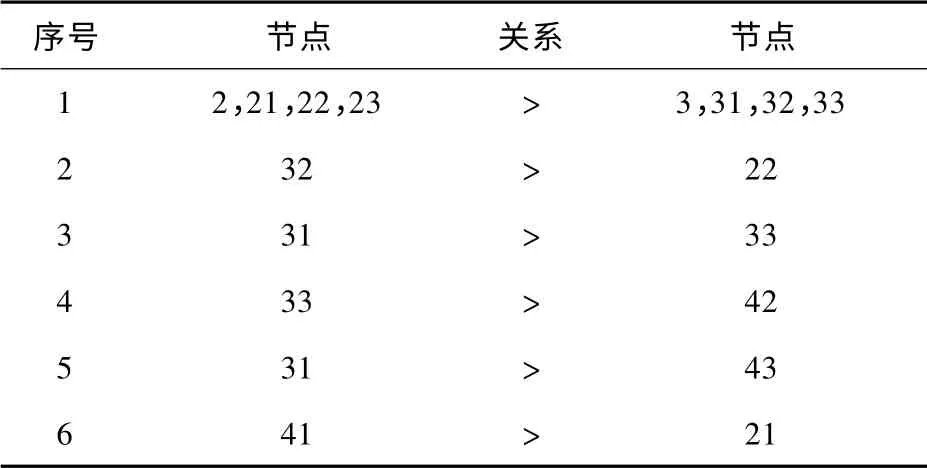
表1 初始节点关系
(2)冲突关系表。分析发现节点32 与节点22关系存在冲突(见表2)。

表2 冲突关系
(3)疏解关系表。对冲突关系疏解后见表3。

表3 疏解关系
3.2 节点初始权重赋值
迭代次数一:
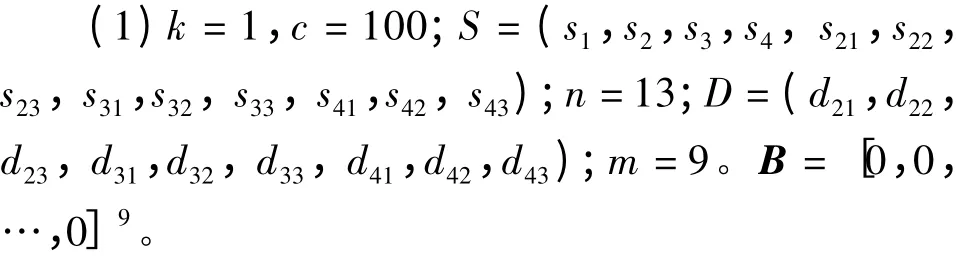
(2)i=1。考察叶节点d21,存在s41>d21,同时存在d21>s3,b21=0。
(3)i= 2。考察叶节点d22,存在d22>s3,b22=0。
(4)i= 3。考察叶节点d23,存在d23>s3,b23=0。
(5)i=4。考察叶节点d31,存在d31>s33,b31=0。
(6)i=5。考察叶节点d32,存在s2>d32,不存在d32>sj(j=1,2,…,n),b32=1。
(7)i=6。考察叶节点d33,存在s2>d33,同时存在d33>s42,b33=0。
(8)i= 7。考察叶节点d41,存在d41>s21,b41=0。
(9)i=8。考察叶节点d42,存在s33>d42,不存在d42>sj(j=1,2,…,n),b42=1。
(10)i=9。考察叶节点d43,存在s31>d43,不存在d43>sj(j=1,2,…,n),b43=1。
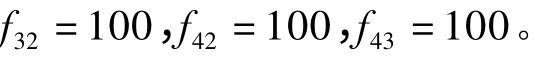
迭代次数二:完善节点关系,由于节点的删除,调整节点关系见表4。
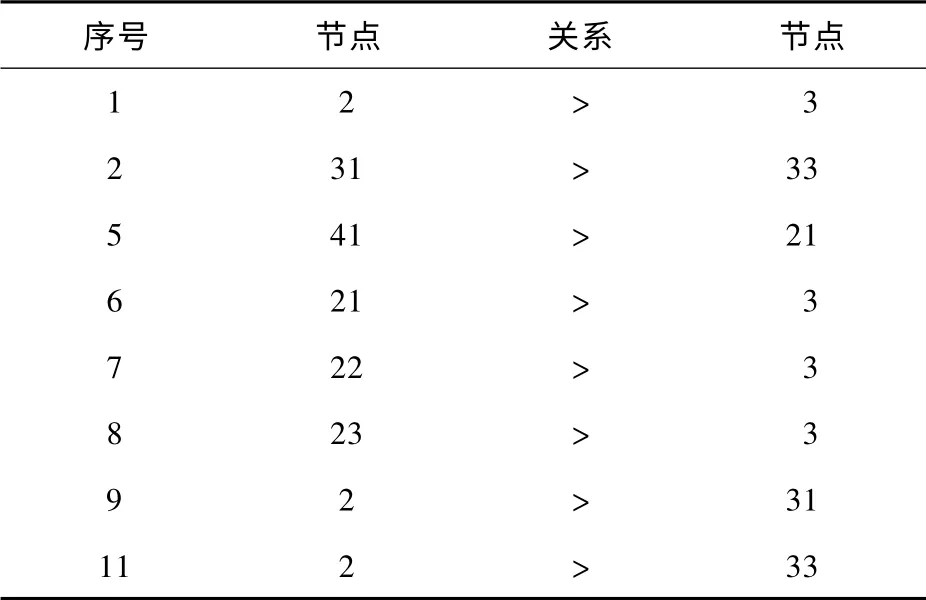
表4 节点关系
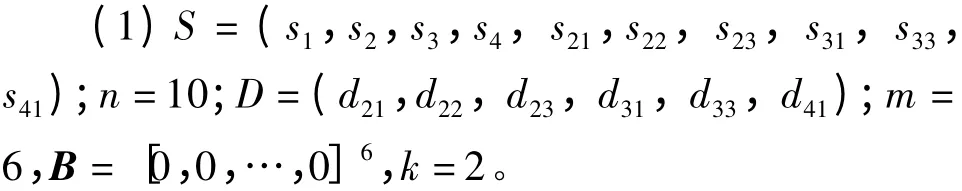
(2)i=1。考察叶节点d21,存在s41>d21,同时存在d21>s3,b21=0。
(3)i= 2。考察叶节点d22,存在d22>s3,b22=0。
(4)i= 3。考察叶节点d23,存在d23>s3,b23=0。
(5)i= 4。考察叶节点d31,存在d31>s33,b31=0。
(6)i=6。考察叶节点d33,存在s2>d33,不存在d33>sj(j=1,2,…,n),b33=1。
(7)i= 7。考察叶节点d41,存在d41>s21,b41=0。
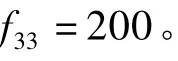
以此类推,迭代次数三、四、五、六,通过6 次迭代,得到如图2 所示权重,方框内数字为节点权重。
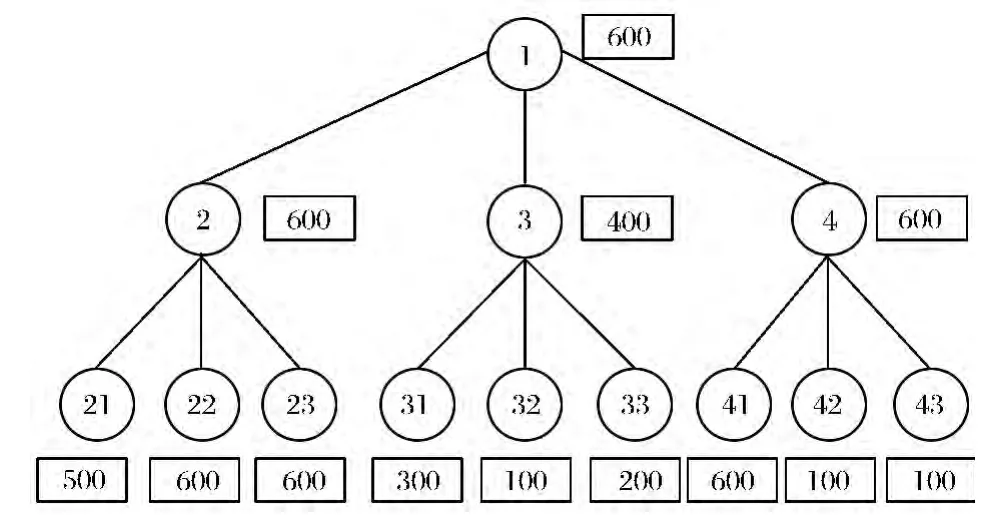
图2 序列树权重
3.3 优先关系搜索
(1)建立权重分层序列树(如图3 所示)。方框内数字为节点的权重与子节点数量。
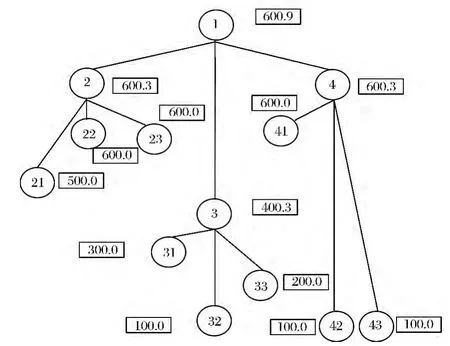
图3 序列树
(2)搜索迭代。
迭代一:
考察第1 层。通过概率选择叶节点22,同时,叶节点22 所有父节点的叶节点数目减一(见表5)。
重复迭代直至九:
考察第5 层。选择叶节点43。由于节点4 没有子节点,选择节点4。同理,由于节点1 没有了子节点,选择节点1(见表6)。
搜索完毕,得到节点序列(22,41,23,21,2,31,33,42,32,3,43,4,1)。对照问题的条件:节点2 >节点3,节点32 >节点22,节点31 >节点33,节点33 >节点42,节点31 >节点43,节点41 >节点21,则有节点2 >节点3,可见该序列完全符合要求。

表5 节点信息熵(迭代一)
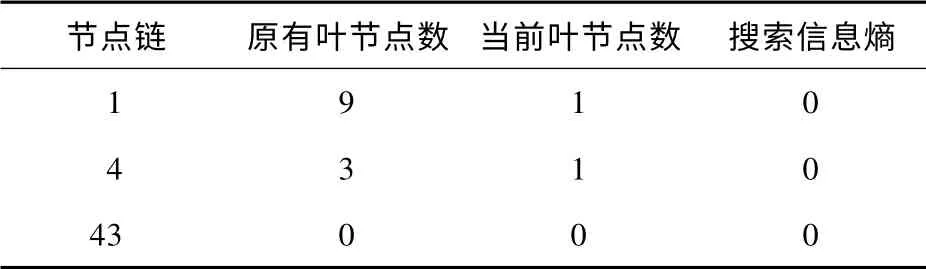
表6 节点信息熵(迭代九)
4 结 语
输送序列是上级指示和首长意图的直接体现,是作战部署的重要内容之一,影响作战企图和作战部署的实现。基于偏序集的拓扑排序能够描述确定输送序列的要求,并通过序列树算法实现输送序列定量化确定。
[1] 曲开社,翟岩慧.偏序集、包含度与形式概念分析[J]. 计算机学报,2006,29(2):119-226.
[2] 叶先一,张福基.偏序集上的一种拓扑排序[J]. 数学研究,2005,38(4):440-443.
[3] 朱立华.并行拓扑排序算法PTSA 的设计与实现[J]. 计算机工程与应用,2004,35(2):111.
[4] 王顺凤.一种有向权图的拓扑排序算法及其应用[J]. 南京气象学院学报,2002,25(5):711-714.
[5] 王晓瑛,魏正军.关于拓扑排序算法的讨论[J].西北大学学报,2002,32(4):344-347.
