城轨车辆车体模态分析

李纯， 张文， 张学山

（1.南京铁道职业技术学院动力工程学院，南京210015；2.北京控股磁悬浮技术发展有限公司，北京100029）

0 引言

城轨车辆在现代交通系统中起着重要的作用，城轨车辆在运行过程中存在不同程度的振动与噪声，这些因素直接影响着车辆运行安全与乘客乘坐舒适度，因此需要对城轨车辆进行相应的动力学分析，由于结构的振动特性决定结构对于各种动力载荷的响应情况，所以在准备进行其它动力分析之前首先要进行模态分析。

模态分析是用来确定结构的振动特性的一种技术，通过模态分析可以使结构设计避免共振，工程师可以认识到结构对于不同类型的动力载荷是如何响应的，有助于在其它动力分析中估算求解控制参数。

1 ANSYS模态分析的方法

车体模态分析主要是预测无阻尼结构的自振频率和振型，可以用来预测共振，也可以为进一步的动力学分析做准备。结构的模态主要取决于结构的质量与分布、结构的刚度。

在ANSYS中有提取模态的方法以下几种：Block Lanczos 法、空间法、缩减法、不对称法、阻尼法［1-2］等。Lanczos法可以在大多数场合中使用，当提取中型到大型模型的大量振型时（>40），此方法经常应用在具有实体、壳单元的模型中，其基本思想是将原特征值问题转化为三对角阵的特征值问题。

采用有限元法分析的动力学问题时，经常采用有限元格式下的动力学微分方程：

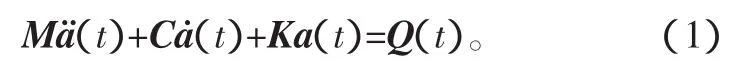
若不计阻尼，则式（1）简化为

则式（2）的解可以写成 a=φsin（t-t0），其中 φ 是 n 阶振型向量，ω是向量φ振动的频率，t是时间变量，t0是由初始条件确定的时间常数。

采用Lanczos算法，特征值可以写成

设Q为由Lanczos向量构成的转换矩阵，若选择的Lanczos向量使Q具有以下性质：

其中，T为三对角阵，则式（3）可以写成

此三对角阵的特征值问题，即可以用标准算法来快速求解。

本文采用自由模态分析构架的固有特性，对车体的模态分析所用的程序是ANSYS软件，采用Lanczos进行固有频率分析。

2 城轨车辆车体模态分析

根据某型城轨车辆的真实设计尺寸［3］，建立了有限元模型如图1。

本文设计了3种模态分析工况，如表1所示。

1）工况1模态分析。铝合金车体空车模态计算，是对车体模型无约束的自由模态计算，共计算20阶模态，从20阶模态分析过滤，将其主要振型和频率列出如图2～图3所示。

图1 整车模型

表13种工况模态分析

2）工况2模态分析。整备模型包括车体结构及附属的车体各种设备等。同空车模态的计算一样，对整备模型进行无约束的自由模态计算，计算前20阶模态，将其主要的振型和频率列出如图4、图5所示。

图2 车体一阶垂向弯曲振动模态（17.22 Hz）

图3 车体一阶扭转振动模态（17.761 Hz）

图4 车体一阶垂向弯曲振动模态（17.224 Hz）

图5 车体一阶扭转振动模态（18.512 Hz）

3）工况3模态分析。超员状态模型包括车体结构及附属的车体各种设备以及超员人数等。同空车模态的计算一样，对整备模型进行无约束的自由模态计算，计算前20阶模态，将其主要的振型和频率列出如图6～图7所示。

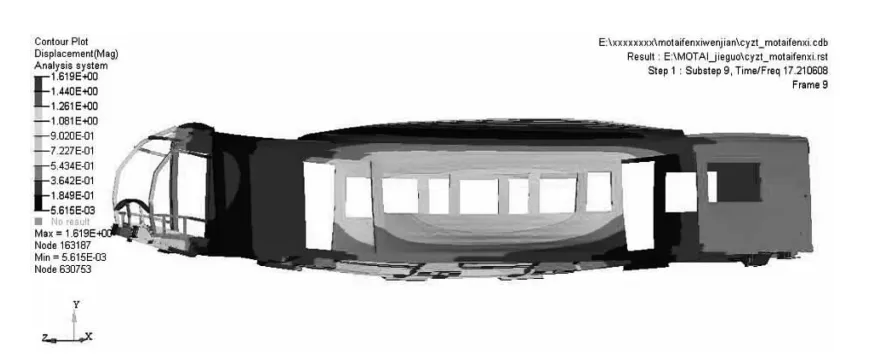
图6 车体一阶垂向弯曲振动模态（17.21 Hz）

图7 车体一阶扭转振动模态（17.389 Hz）

3 结论

1）模态分析对于车辆设计来说十分重要，它可以模拟真实工况下的车辆受力与变形状态，能够给设计者提供有意义的参考依据。

2）本文设计了3种模态分析的工况，对车体进行了模态分析，结果表明：a.铝合金车体空车的一阶垂向弯曲振型频率17.22 Hz，一阶扭转为17.761 Hz；b.整备状态下车体的一阶垂向弯曲振型频率17.224 Hz，一阶扭转为18.512 Hz；c.超员状态下车体的一阶垂向弯曲振型频率17.21 Hz，一阶扭转为17.389 Hz。

根据相关文献可知，空气弹簧的固有振动频率为1～2Hz［4］，而转向架模块的一阶垂向弯曲振动频率为51.429［4］。因此车体、空气弹簧、转向架之间一阶模态固有频率差别显著，不存在共振的可能，也就是说，车体结构设计合理。

［1］ 方远翔，陈安宁.振动模态分析技术［M］.北京：国防工业出版社，1993.

［2］ 朱安文，曲广吉.结构动力模型修正技术的发展［J］.力学进展，2002，32（3）：337-347.

［3］ 林田聪.欧洲铁路开发新的车辆结构［J］.国外铁道车辆，2002，39（6）：12-14.

［4］ 大连交通大学.CMS04磁浮车单转向架强度、刚度及模态计算报告［R］.2007.