后台阶流的水动力特征
2014-12-23吴时强樊新建吴修锋
肖 潇,吴时强,樊新建,吴修锋
(南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏南京210029)
后台阶流动是一种经典的分离流动,也是工程实际中常见的流动形态,如坝面溢流、风吹过建筑物、管道中的突扩等.在这些情况中,流动通过台阶时会发生分离,台阶角部形成回流涡,且在流体绕过旋涡后重新与壁面接触,然后继续沿着墙壁流动.后台阶流动包含着丰富流动现象.前人对后台阶流动已经做了大量研究.B.F.Armaly[1]等利用 LDV 技术测量了后台阶流动流场,分析了回流区长度.K.Akselvoll等[2-3]采用大涡模拟技术研究了后台阶流动流态.H.Le等[4-5]采用直接数值模拟研究了后台阶流动.T.Lee等[6]利用实验和数值研究,分析了后台阶流动情况.T.P.Chiang 等[7-8]通过数值模拟研究了雷诺数范围为50≤Re≤2 500的层流情况下后台阶流动.H.Iwai等[9]研究了不同倾斜角度对后台阶流动的影响.P.G.Spazzini等[10]研究了后台阶流动的稳定性.D.Barkley等[11]分析了三维后台阶流动的稳定性.笔者基于商业软件FLUENT,采用三维数值模型,在模型验证计算的基础上,模拟计算不同雷诺数下台阶流动,分析后台阶流动结构,探讨台阶流动水力特性.
1 三维紊流数学模型
后台阶流动的三维几何模型如图1所示.参照台阶流动模型试验装置[12],试验装置为自循环系统[8-9],材料为1 cm厚的有机玻璃,台阶高度为3.3 cm,台阶前流道高度为 6.6 cm,台阶后流道高度为9.9 cm,台阶宽度为20.0 cm.流道进口距台阶2.4 m,流道出口距台阶2.8 m.试验采用PIV系统,对台阶后的中心对称面的流场进行测量.

图1 后台阶流动计算区域
1.1 基本方程
采用三维k-ε紊流模型,模拟后台阶流动.针对不同雷诺数下流动特性,选用不同的紊流模型,当Re≤2 300时,采用层流模型模拟,当Re>2 300时,采用RNGk-ε模型模拟.控制方程(时均量均略去时均符号)如下:
连续方程为

动量方程为

式中:t为时间;ui,uj为速度分量;xi,xj为坐标分量;ρ为密度;p为压力;fi为质量力.
k方程为

式中:μ为分子黏性系数;σk=0.717 9;μt=ρvt=
ε方程为

1.2 数值方法
控制方程通过有限体积法进行离散,形式为

式中:φ为通用变量,如速度、紊动能等;Γφ为φ的扩散系数;Sφ为方程源项.
先对上面方程式在任意控制体积V(其边界为A)作体积分,利用高斯定理将体积分化成面积分.记F(φ)=ρφu-Γφgrad φ,得有限体积法(FVM)的基本方程为

对控制体积单元取平均后,可离散得到FVM基本方程的最终形式为
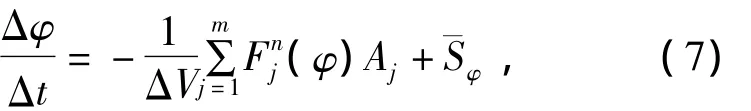
式中:ΔV为单元体积;m为单元面总数;Aj为单元面j的面积;¯Sφ为单元源项平均值;单元面j的法向通量为Fj=Fj(φ)·n,包括对流流量和扩散通量.
速度压力耦合采用由 S.V.Patankar[13]提出的SIMPLE算法进行求解.
1.3 网格布置
计算区域采用结构网格布置,在靠近边界层和台阶处网格布置密集,这样可以保证计算速度,网格数大约为184 800个,如图2所示.

图2 计算网格
1.4 边界条件
进口边界:进口采用速度入口条件,紊动能k和耗散率ε分别为

式中u0为进口处的平均速度;
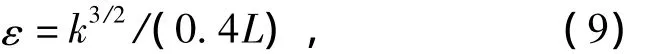
式中L为特征长度,即水力半径[14-15].
出口边界:出口水流采用自由出流条件.壁面条件:上下边界均为固壁不滑移边界.
2 结果分析
由二维PIV采集系统获得试验数据,选取较典型的层流区下Re=1 480和紊流区下的Re=19 050的实测数据与模拟结果进行对比,进而对数学模型模拟结果与相应的物理模型模拟结果进行验证,分析其中的规律,以得到相应结论.
2.1 流动结构
模拟计算雷诺数为100~50 000内包含层流区、过渡区和紊流区等不同流态的后台阶流动.雷诺数的定义为

式中:¯u为进口截面速度的平均值;h为台阶高度;υ为运动黏性系数.
Re=1 480和9 050时台阶后定常流时均流场结构模拟计算结果与实测结果比较情况如图3所示,选取中心剖面分布,不同雷诺数条件下水流流场结构具有共性:在台阶下游均形成大小不同的稳定回流区;回流区内均存在回流涡,回流涡的尺寸与台阶高度为同一个量级;位于剪切层以上的主流在台阶下游附近处和再附着区的下游处均较为平顺,并且在再附着区处稍有弯曲.同时也发现不同雷诺数条件下流场的不同之处:低雷诺数情况下,漩涡形状不稳定、不规则,随着雷诺数的增大形状越来越规则,并趋于稳定.
流场结构的数值计算结果与实测值基本一致.在低雷诺数条件下,计算结果和实测结果差异略大,高雷诺数条件下,吻合较好,这些差异产生的原因可能是由于低雷诺数条件下所采用的数学模型不尽完善,有待改进.
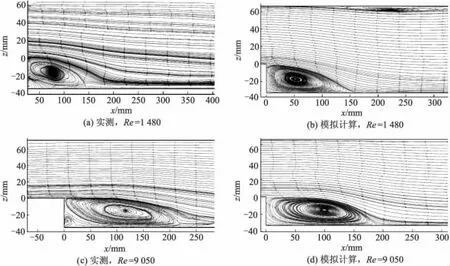
图3 台阶后时均流场结构图
2.2 回流区特性
由于台阶处边界突变,流动边界层在台阶角点处发生分离,在台阶下游形成主回流区.分离后的剪切层在流动方向迅速扩散,于台阶下游L处与壁面再附着.分离再附区长度L与Re的关系如图4所示,计算值与试验值与文献[1]的总体趋势一致.在Re≤800时上升,在800<Re≤2 500降低,在Re>2 500上升,最后L趋于一个稳定值6.5h左右.

图4 分离再附区长度与Re的关系曲线
2.3 速度分布
Re=1 480和9 050时中心剖面的时均流速等值线分布如图5所示.在台阶角部回流区,流速较小,在回流区底部位置速度稍偏大,这是由于离心运动造成的.在10h后的下游流道中断面速度再次恢复均匀.

图5 中心剖面时均流速等值线图
Re=1 480,和9 050时中心剖面处距台阶1h,3h,5h,7h的垂向时均流速变化如图6所示,u为速度,u0为进口处断面平均速度.速度变化呈S型分布,在5h与7h之间,流速变化很大,Re=9 050时比Re=1 480时速度变化更为显著,不同Re下速度总体上计算结果与试验值吻合良好,Re=1 480中距台阶1h处断面差异较大,是由于该处在PIV测量范围的边界处,试验数据有些误差.

图6 中心剖面时均断面速度分布图
2.4 压力分布
Re=1 480和9 050时中心剖面的时均压力等值线分布图如图7所示.压力沿程变化是增加的,在底部增加得稍快.在台阶角点处出现压力最小值,即分离流的起点位置.另外,压力在旋涡中心区的位置压力也较小.
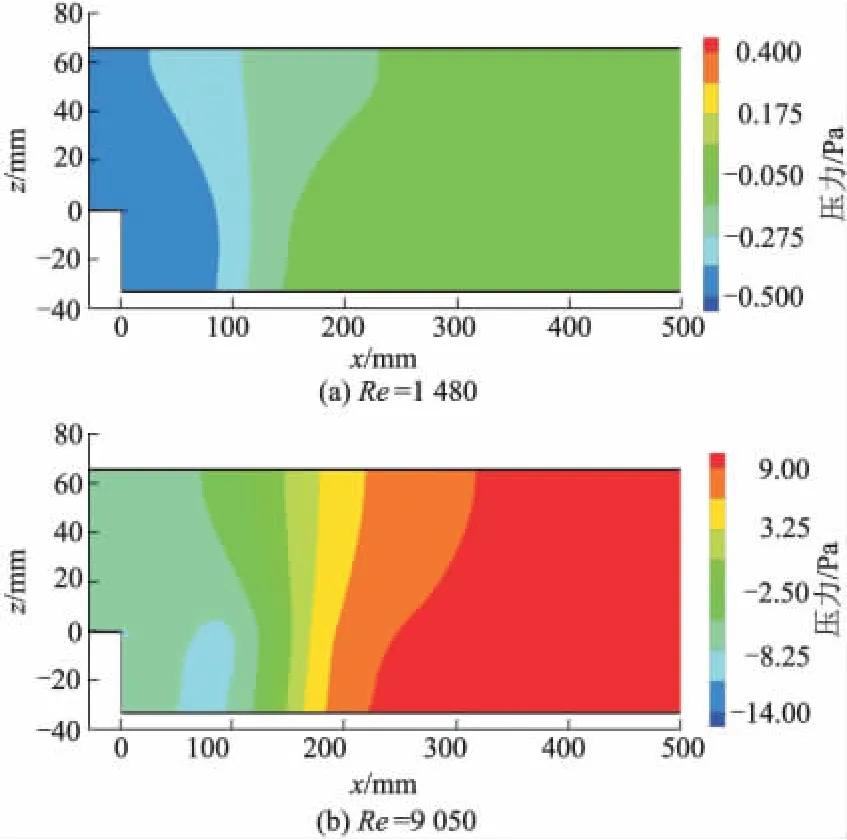
图7 中心剖面的时均压力等值线图
2.5 紊动能分布
Re=1 480和9 050时中心剖面紊动能等值线如图8所示.在台阶高度以下位置紊动能较强、不均匀,在旋涡中心紊动能最强.在台阶高度以上除顶部壁面的紊动能较大,整个断面紊动能较小、均匀.

图8 中心剖面的紊动能等值线图
2.6 涡量特性
Re=1 480和9 050时中心剖面的涡量等值线如图9所示,在贴近壁面的涡量较大,且在台阶角点后涡量沿着壁面扩散,随着Re增大,涡量值也增大.

图9 中心剖面的涡量等值线图
3 结论
1)根据流场结构、回流长度变化及速度的实测值与模拟值对比可以看出:两者在回流区的结构基本相同,回流长度变化趋势比较一致,断面流速值总体吻合较好,该模型能很好地模拟后台阶流动问题.
2)后台阶流的回流区长度在Re≤800时呈增长趋势,在800<Re≤2 500时呈减小趋势,在Re>2 500后缓慢增长并趋于一稳定值约为6.5h.
3)在低雷诺数情况下,断面速度波峰较陡,压力沿程变化较小,紊动能小,后台阶处涡量变化不明显;在高雷诺数情况下,断面速度波峰较缓,压力沿程变化较强,回流区中压力变化明显,紊动能大,后台阶处涡量变化显著.
References)
[1]Armaly B F,Durst F,Pereira J C F,et al.Experimental and theoretical investigation of backward-facing step flow[J].J Fluid Mech,1983,127:473-496.
[2]Akselvoll K,Moin P.Large-eddy simulation of turbulent confined coannular jets[J].J Fluid Mech,1996,315:387-411.
[3]Addad Y,Laurence D,Talotte C,et al.Large eddy simulation of a forward-backward facing step for acoustic source identification[J].International Journal of Heat and Fluid Flow,2003,24:562-571.
[4]Le H,Moin P,Kim J.Direct numerical simulation of turbulent flow over a backward-facing step[J].J FluidMech,1997,330:349-374.
[5]Ding Daoyang,Wu Shiqiang.Direct numerical simulation of turbulent flow over backward-facing step at high Reynolds numbers[J].Science China:Technological Sciences,2012,55(11):3213-3222.
[6]Lee T,Mateescu D.Experimental and numerical investigation of 2-D backward-facing step flow[J].Journal of Fluids and Structures,1998,12:703-716.
[7]Chiang T P,Sheu T W H.A numerical revisit of backward-facing step flow problem[J].Physics of Fluids,1999,11:862-873.
[8]Chiang T P,Sheu T W H,Fang C C.Numeical investigation of vortical evolution in a backward-facing step expansion flow[J].Applied Mathematical Modelling,1999,23:915-932.
[9]Iwai H,Nakabe K,Suzuki K,et al.The effects of duct inclination angle on laminar mixed convetive flows over a backward-facing step[J].International Journal of Heat and Mass Transfer,1999,43:473-485.
[10]Spazzini P G,Luso G,Onorato M,et al.Unsteady behavior of back-facing step flow[J].Experiments in Fluids,2001,30:551-561.
[11]Barkley D,Gabriela M,Gomes M,et al.Three-dimensional instability in flow over a backward-facing step[J].J Fluid Mech,2002,473:167-190.
[12]肖 潇,樊新建,吴时强.基于k-ε紊流模型的后台阶流流动特性研究[J].水利水运工程学报,2013(3):25-30.Xiao Xiao,Fan Xinjian,Wu Shiqiang.Hydraulic characteristics of backward-facing step flow based onk-ε turbulence model[J].Hydro-Science and Engineering,2013(3):25-30.(in Chinese)
[13]Partanker S V.Numerical Heat Transfer and Fluid Flow[M].New York:McGraw-Hill,1980.
[14]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004.
[15]张金凤,梁 赟,袁建平,等.离心泵进口回流流场及其控制方法的数值模拟[J].江苏大学学报:自然科学版,2012,33(4):402-407.Zhang Jinfeng,Liang Yun,Yuan Jianping,et al.Numerical simulation of recirculation control at centrifugal pump inlet[J].Journal of Jiangsu University:Natural Science Edition,2012,33(4):402-407.(in Chinese)
