指数形式渗流定律下软土一维大变形固结分析
2014-12-23李传勋苗永红
李传勋,徐 超,苗永红
(江苏大学土木工程与力学学院,江苏镇江212013)
土层中的有效应力σ'为
深厚软土层作用有较大荷载时,地基就会发生较大的沉降变形,此时已超出了传统小应变固结理论的适用范围.自从大变形固结这一研究领域的开拓者R.E.Gibson等给出物质坐标下以孔隙比为控制变量的一维大应变固结普遍方程以来[1],国内外学者对其展开了深入的研究[2-8].然而,目前几乎所有一维大变形固结理论均是建立在达西定律基础之上,对软粘土中存在非达西渗流的一维大变形固结理论还鲜见报道.李传勋等[9-11]先后对基于指数形式渗流定律的软土线性及非线性固结理论进行了研究,但均没有考虑软土的大变形固结特性.
本研究基于指数形式渗流定律,在拉格朗日坐标系下,以超静孔压为变量建立软土一维大变形固结理论,并分析渗流指数m对大变形固结性状的影响,以及指数形式渗流定律下大、小应变固结理论的区别.
1 问题的描述
厚度为H0的深厚软土层在自重应力和初始表面荷载qp作用下变形已稳定,地下水初始水位高于基准面Hw.软土层顶面透水,底面不透水.拉格朗日和流动坐标系如图1所示.图1中S(0,t)为地基顶面t时刻的沉降值.拉格朗日坐标系a及流动坐标系ξ均以向下为正(重力方向),并将地基表面作为流动坐标系的基准面(ξ=0).软土层顶面和底面在拉格朗日坐标系中分别记为a=0和a=H,而在流动坐标系下分别记为ξ=S(0,t)(初始时刻为ξ=0)和ξ=H0.随时间变化的荷载q(t)作用于地基表面,其初始值为q0,超过加载历时为tc后,保持qu不变.
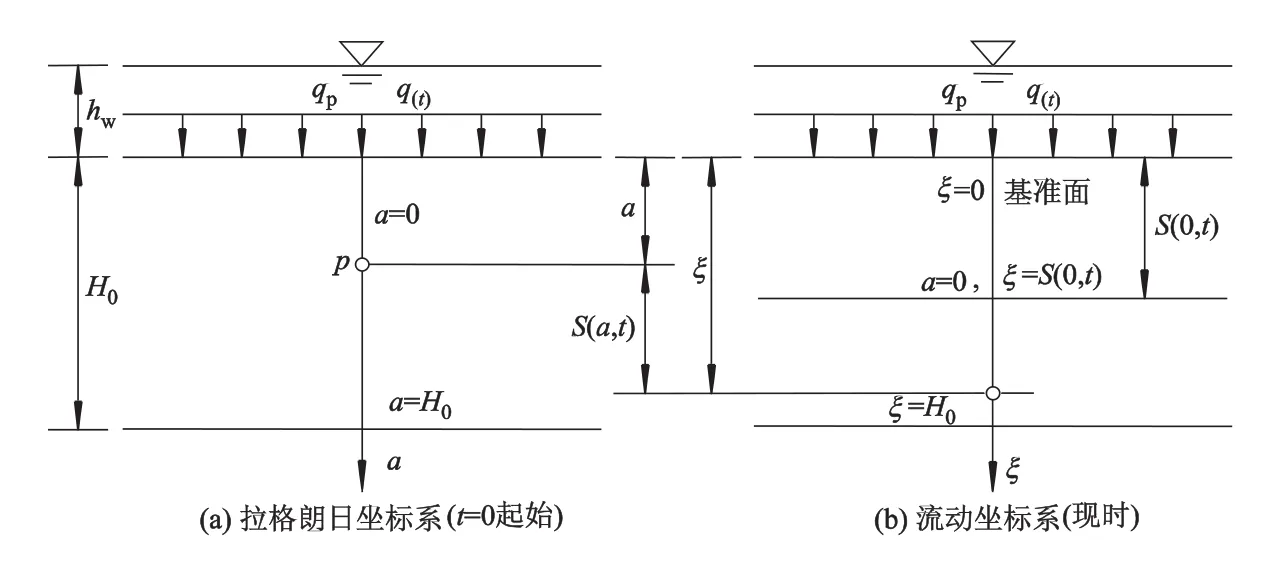
图1 拉格朗日坐标系与流动坐标系
由图1 知:ξ与a,S(a,t)之间的关系为[5]

式中:S(a,t)为拉格朗日坐标系中坐标a在t时发生的地基沉降.
根据 R.E.Gibson等的研究[1],ξ与a间关系为

式中:e=e(a,t)是拉格朗日坐标系中a处在t时的孔隙比;e0=e(a,0)是t=0时的初始孔隙比.
2 指数形式渗流定律下大变形固结控制方程
根据 Xie K.H.等[5]对以上问题研究,土层中总应力σ与孔隙水压力p分别为

式中:σ(0,t)=qp+q(t)+γw(Hw+S(0,t));Gs为土粒比重.u=u(a,t)是由外荷载引起的超静孔隙水压力;pw为静水压力,pw=γw(Hw+S(0,t))+
土层中的有效应力σ'为

同文献[9-11]假定土中渗流遵循指数形式渗流定律,即v=-kvim,其中v为渗流速度,kv为渗透系数;i为水力坡降,m为指数大小.渗流定律中的流速应为整个断面的平均流速,故指数形式渗流定律在流动坐标系下表达为

式中:vw,vs分别为孔隙水和土颗粒相对于基准面的速度;u为超静孔隙水压力;γw为水的重度.
一般工程荷载下,固体颗粒和水自身压缩很小,故本研究不考虑土颗粒和土中水自身的压缩变形,此时流动坐标系下连续方程为

式中:e为ξ处孔隙比.
考虑流动坐标系下边界条件的引入较难,一般均在拉格朗日坐标下对方程进行解答,根据坐标系之间转换关系,式(7)转化为

目前关于土中非达西渗流软土大变形固结研究较少,遵循从简至难原则,假定土体在固结过程中体积压缩系数与渗透系数均保持不变,这虽与实际土体有较大差别,但对初步认识土体在指数形式渗流定律下大变形固结性状尤为重要.故

将式(5)、(9)、(10)代入式(8),可得到基于指数形式渗流定律的软土大变形固结问题在拉格朗日坐标下的控制方程,即

对式(9)进行积分,得

或

式中:e00=e(0,0)为初始时刻地基土层顶面孔隙比.由式(12)、(13)进一步得到:

将式(14)、(5)中的σ'0表达式联立,得σ'0表达式:

将式(15)代入式(14),得

式(12)进一步改写为

将式(17)代入式(11),得

式(18)即为在以上假定下考虑指数形式渗流定律的软土大变形固结问题的控制方程.地基顶面排水、底面不透水下,其求解条件为

方程(18)为二阶非线性偏微分方程,很难得到其解析解,本研究应用有限差分法求其数值解.
3 方程的有限差分解
为方便数值求解,定义如下无量纲变量:
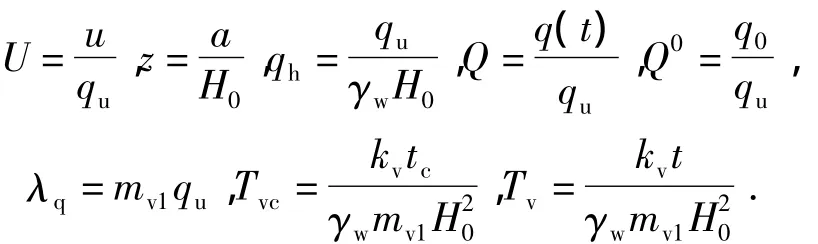
对于单级加载,无量纲变量Q为
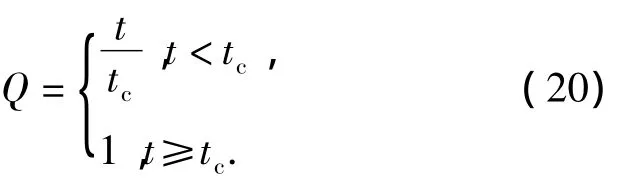
应用以上无量纲变量,控制方程(18)及求解条件式(19)可分别转化为

将整个土层从表面开始,划分为n个薄层,每个薄层厚度为Δz,第k个时段增量为Δtvk,利用拟线性偏微分方程的隐式格式,可以将式(21)离散为
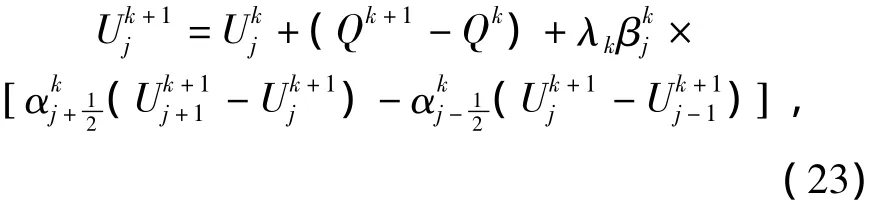
式中:1≤j≤n;k=0,1,2,3,…;Ukj为第j薄层在第k时段超静孔隙水压力的无量纲值;Qk为第k时段外荷载的无量纲值
求解条件式(22)应用离散点可表示为

根据式(16)、(12),第j薄层初始孔隙比e0j及tk时土体孔隙比ejk分别为

从式(26)发现第j层土体的最终孔隙比为

根据式(1)得

将式(2)代入式(28),积分可得地基表面处tk时沉降变形值:

在荷载作用下地基发生的最终总沉降变形为

大应变按变形定义的地基平均固结度Us为

大应变按应力定义的地基平均固结度Up为

由式(31)、(32)可见:指数形式渗流定律下,软土大变形固结理论中按变形定义的地基平均固结度与按孔压定义的平均固结度不再相等,这与文献[9]的小应变固结理论不同.
4 算例分析
4.1 指数对固结性状的影响
基于以上差分解答,通过算例对基于指数形式渗流定律的软土一维大应变固结问题进行计算分析,其中土工参数取值与文献[5]相同,即Gs=2.75,H0=10 m,Hw=1m,e00=3.0,Tvc=0.05,qp=10 kPa,qu=100 kPa,kv0=10-9m·s-1,mv1=4 MPa-1.
图2 为不同m时,分别在Tv=0.2,0.6 时,超静孔隙水压力沿深度的分布曲线.图3为平均固结度Up与时间因子Tv关系曲线.由图2知:固结初期(Tv=0.2)m越大,土中残留的超静孔隙水压力越小;固结后期(Tv=0.6)m越大,土中残留的超静孔隙水压力越大.与此固结性状相对应,固结速率在固结初期随m增加而加快;在固结后期固结速率随m的增加而减慢,见图3.

图2 不同m时的超孔压分布曲线
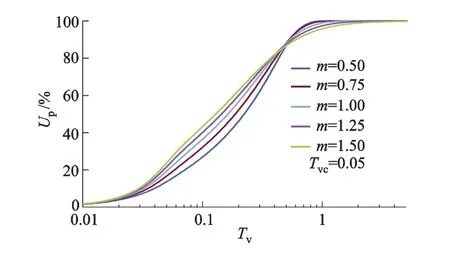
图3 Up-Tv关系曲线
图4为不同m时孔隙比分布曲线.图5为平均固结度Us与时间因子Tv关系曲线.由图4知:在固结初期(Tv=0.2)土体的孔隙比随m增大而减小;在固结后期(Tv=0.6)土体的孔隙比随m增大而增大.与此相对应,按变形定义的平均固结度在固结初期随着m增加而增大;在固结后期平均固结度随着m增加而减小(图5).
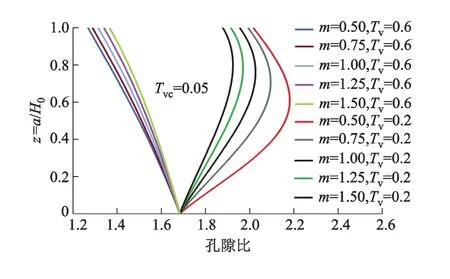
图4 不同m时孔隙比分布曲线
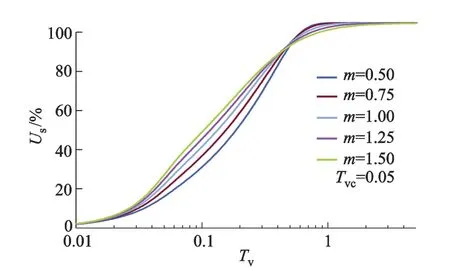
图5 Us-Tv关系曲线
4.2 大、小应变固结理论的区别
在土中渗流遵循指数形式渗流定律下,分别应用文献[9]的小应变线性固结理论和本研究的大应变固结理论计算地基平均固结度与沉降曲线,如图6所示.由图6知:大应变固结理论下,以变形定义的地基平均固结度要比以应力定义的地基平均固结度快;且无论是以变形还是以应力定义,大应变固结理论下土体的固结速率均要比小应变固结理论快.特别需要说明的是,大、小固结理论固结速率的差异会随着土体压缩性及荷载的不同而发生变化,土体压缩性越大,两者之间的差异越大;作用于地基表面的荷载越大,则两者之间的差异也越大.如果土体的压缩性很低,且作用于地基的荷载也很小(λq值很小),此时大、小应变固结理论计算得到的固结曲线则相差无几.
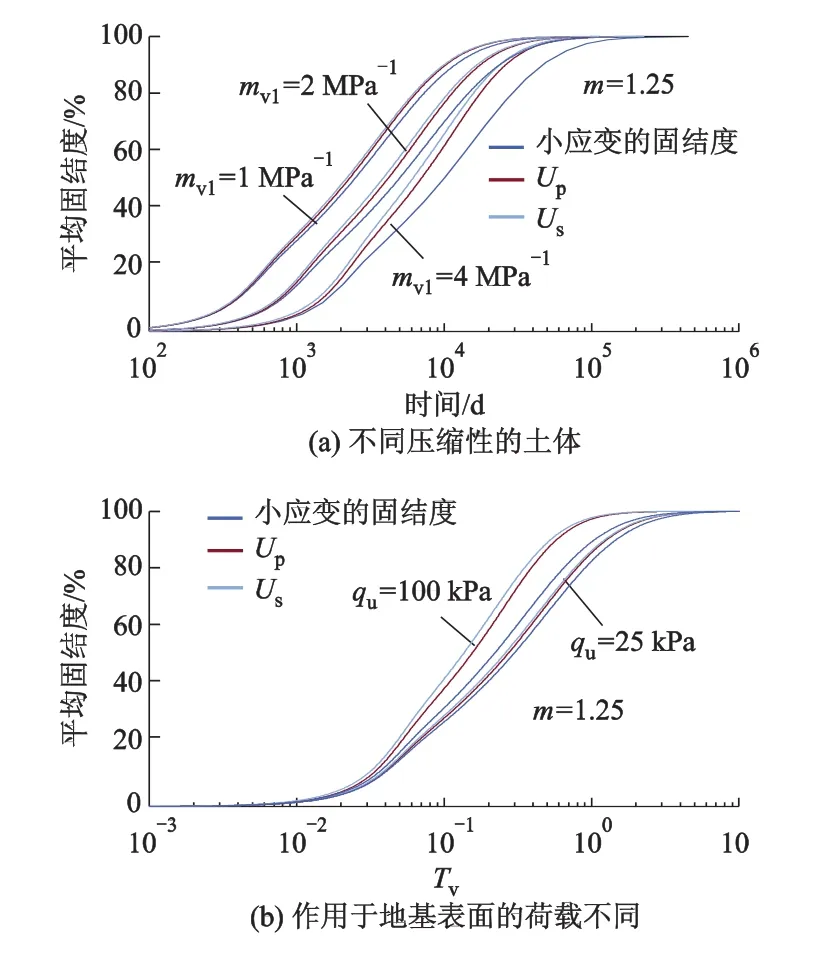
图6 大、小变形固结理论的固结度与时间曲线
图7为地基沉降曲线.指数形式渗流定律下的小应变线性固结理论中,地基的最终沉降量S∞=mvquH0,容易发现如果mvqu>1(即 λq>1),此时地基的沉降量将比土层厚度还要大,这明显不符合实际,即土体压缩性或荷载较大时,仍然应用小应变固结理论会存在较大计算误差.如果土体压缩性很小(图7a中mv1=1 MPa-1),或者作用于地基的荷载很小(图7b中qu=25 kPa),分别应用大、小应变固结理论计算的地基沉降曲线基本一致.但是,随着土体压缩性或者荷载增大,两者计算的沉降曲线之间的差异会越来越大,此时必须要采用大应变固结理论计算地基的固结沉降变形.
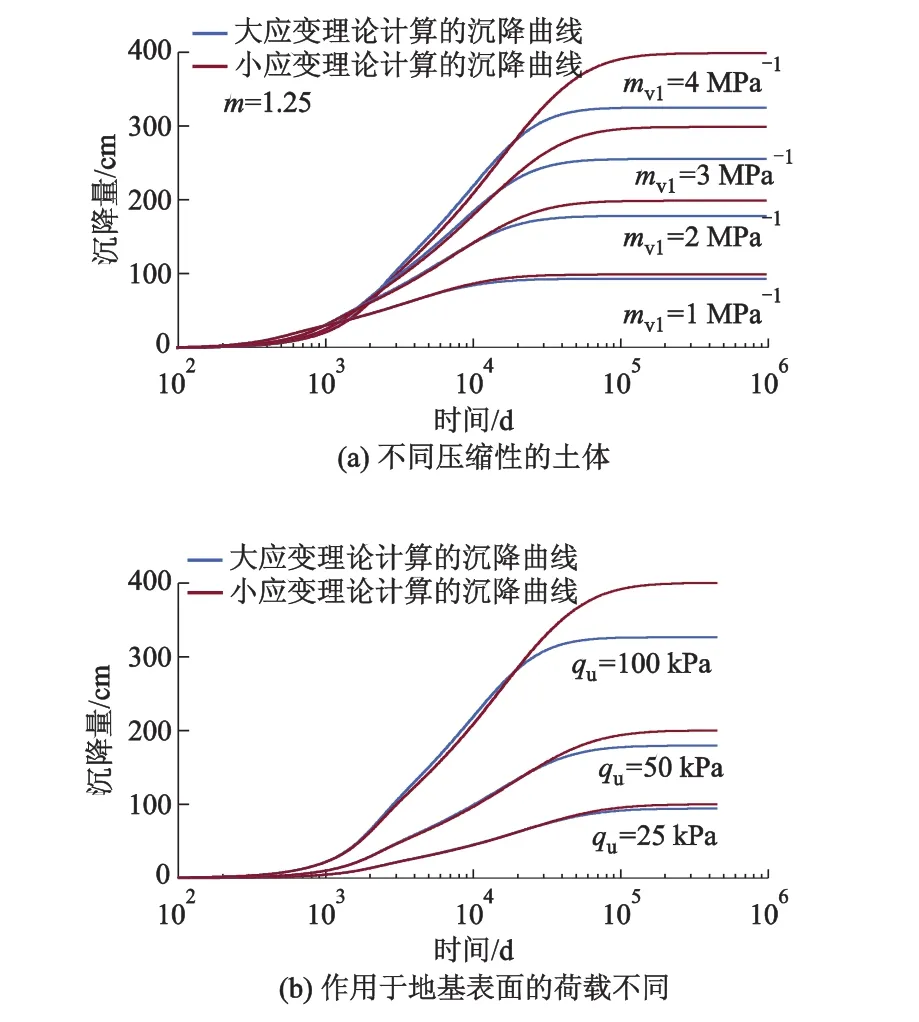
图7 大、小变形固结理论的地基沉降曲线
5 结论
1)与指数形式渗流定律下小应变线性固结理论不同,大应变固结理论中,按变形定义的地基平均固结度与按孔压定义的地基平均固结度不再相等,且相同时间因子下按变形定义的地基平均固结度要大于按孔压定义的地基平均固结度.
2)在土中渗流遵循指数形式渗流定律的前提下,土体固结速率在固结初期随着指数增加而加快;在固结后期固结速率随着指数增加而减慢.
3)大、小变形固结理论下,土体固结速率之间的差异会随着土体压缩性及作用于地基表面荷载的增大而加剧,且大变形固结理论计算得到的沉降曲线理论上更加合理.
References)
[1]Gibson R E,Schiffman R L,Cargill K W.The theory of one-dimensional consolidation of saturated clays:II.finite nonlinear consolidation of thick homogeneous layers[J].Canadian Geotechnical Journal,1981,18(2):280-293.
[2]Morris P H.Analytical solutions of linear finite-strain one-dimensional consolidation[J].Journal of Geotechnical and Geoenvironmental Engineering,2002,128(4):319-326.
[3]Morris P H.Analytical solutions of linear finite-and small-strain one-dimensional consolidation[J].International Journal for Numerical and Analytical Methods in Geomechanics,2005,29(2):127-140.
[4]Cai Y Q,Geng X Y,Xu C J.Solution of one-dimensional finite-strain consolidation of soil with variable compressibility under cyclic loadings[J].Computers and Geotechnics,2007,34(1):31-40.
[5]Xie K H,Leo C J.Analytical solutions of one-dimensional large strain consolidation of saturated and homogeneous clays[J].Computers and Geotechnics,2004,31(4):301-314.
[6]李冰河,应宏伟,谢康和,等.考虑土体自重的一维大应变固结分析[J].土木工程学报,2000,33(3):54-59.Li Binghe,Ying Hongwei,Xie Kanghe,et al.Analysis of 1-D large-strain consolidation considering the selfweight of soils[J].China Civil Engineering Journal,2000,33(3):54-59.(in Chinese)
[7]丁洲祥,袁大军,朱合华.一维大变形主、次固结耦合新模型[J].岩土力学,2010,31(8):2367-2372.Ding Zhouxiang,Yuan Dajun,Zhu Hehua.A novel coupling model for 1D finite-strain primary-secondary consolidation[J].Rock and Soil Mechanics,2010,31(8):2367-2372.(in Chinese)
[8]王 伟,宰金珉,卢廷浩.软土工后沉降双曲线模型与指数曲线模型分析[J].江苏大学学报:自然科学版,2008,29(2):173-176.Wang Wei,Zai Jinmin,Lu Tinghao.Analysis on hyperbolic model and exponential model for post-construction settlement of soft soil[J].Journal of Jiangsu University:Natural Science Edition,2008,29(2):173-176.(in Chinese)
[9]李传勋,谢康和,卢萌盟,等.变荷载下基于指数形式渗流的一维固结分析[J].岩土力学,2011,32(2):553-559.Li Chuanxun,Xie Kanghe,Lu Mengmeng,et al.Onedimensional consolidation analysis considering exponential flow law and time-depending loading[J].Rock and Soil Mechanics,2011,32(2):553-559.(in Chinese)
[10]李传勋,谢康和,卢萌盟,等.变荷载下基于指数渗流双层地基一维固结分析[J].岩土力学,2012,33(5):1565-1571.Li Chuanxun,Xie Kanghe,Lu Mengmeng,et al.Analysis of one-dimensional consolidation of double-layered soil with exponential flow considering time-dependent loading[J].Rock and Soil Mechanics,2012,33(5):1565-1571.(in Chinese)
[11]李传勋,谢康和,胡安峰,等.基于指数形式渗流定律考虑初始有效应力非均匀分布的软土一维非线性固结分析[J].岩石力学与工程学报,2012,31(S1):3270-3277.Li Chuanxun,Xie Kanghe,Hu Anfeng,et al.Analysis of one-dimensional nonlinear consolidation of soft considering exponential flow law and non-uniform distribution of initial effective stress[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S1):3270-3277.(in Chinese)
