FFU内部结构优化的数值模拟和试验

王军锋，胡维维，张 铮，吴 琦

(江苏大学能源与动力工程学院，江苏镇江212013)

风机过滤单元是一种具有过滤功效、自带动力的模块化的末端送风装置.风机从FFU顶部将空气吸入并经过滤膜过滤，过滤后的洁净空气在整个出风面以(0.45 ±0.000 9)m·s-1的风速均匀送出，以满足洁净室对空气质量的要求.FFU方式比常规的空调机组集中送风方式节省运行成本30%以上［1-2］.

在性能方面，其风量、余压、噪声、效率等参数之间相互关联、相互制约［3］，目前存在的问题是 FFU内部流道的不合理导致流动的紊乱，产生了大量的能量损耗及噪声，同时导流装置的不合理设计导致出口风速的不均匀，严重影响了室内的净化效率.而对FFU内部结构进行优化设计能有效提高整体性能和能量利用率［4］.笔者选取了一款国内应用比较广泛的FFU进行研究，旨在为FFU的节能设计及性能优化提供一定的参考.

试验研究的方法能够真实地反映设备的运行状况和一些外特性，林忠平等［5］通过试验对FFU的结构组件对性能的影响作了探讨，Liu Junjie等［6］采取加均流板的形式来保持风机过滤器机组的面风速均匀性及减少面风速的湍流度.但单纯的试验方法不能直观显示内部流动，较难提出有针对性的优化方案.数值模拟能预测出内部流场［7-10］，国内外关于FFU数值模拟的文献主要集中在FFU对室内气流组织的影响上［11-13］，单纯对FFU内部进行模拟的研究很少.而且模拟结果与实际情况也会存在有一定误差，笔者采用数值模拟与试验研究相结合的方法，利用CFX软件模拟FFU内部流场，然后提出优化方案，并再次模拟以确认修改的有效性，最终将修改方案应用到实际产品中，并用检测平台来评价其性能.

1 数值模拟

1.1 物理模型

准确的几何模型是数值模拟的基础，直接影响到数值计算结果的精确性和可靠性.由于后期需要对模拟结果进行试验验证，所以物理模型完全按照实物尺寸进行建立，如图1所示.

图1 物理模型

使用三维软件pro/e进行建模，模型分为5个部分:入口、叶轮、主体、过滤器和出口.入口和出口都进行了加长，以保证进、出口流体都能达到稳定状态，有利于计算的收敛.使用ICEM划分网格，其中入口、叶轮、过滤器和出口这4部分由于结构比较规则，划分为结构化网格，即每个单元都为六面体，这样网格数量就较少且有利于计算的收敛.对于主体部分，由于内部结构比较复杂，划分成结构化网格比较困难，故采用非结构化网格，每个网格单元都为四面体.各部分之间使用Interface(交界面)进行连接.

1.2 数学模型

FFU内部的流动是典型的湍流流动，选用的湍流模型是标准k-ε模型.k-ε模型需要求解湍动能及其耗散率方程.湍动能输运方程是通过精确的方程推导得到，但耗散率方程是通过物理推理，数学上模拟相似原形方程得到的.该模型假设流动为完全湍流，分子黏性的影响可以忽略.因此，标准k-ε模型只适合完全湍流的流动过程模拟，对于壁面区域采用壁面函数法.

1.3 模型设置求解及边界条件

工作流体设为25℃的空气，各物性参数为软件自带参数.入口采用速度入口边界条件，根据实测数据确定入口来流的平均速度为3.2 m·s-1，出口采用压力出口边界条件，平均静压为0 Pa.过滤膜阻力为120 Pa，采用多孔介质模型，阻力系数设为10 050 kg·m-4.壁面采用无滑移壁面边界条件，近壁区的处理采用壁面函数法.各区域之间采用交界面进行连接，具体连接模式为GGI模式.

2 模拟结果可靠性验证

计算结果的准确性是后续优化的基础，因此首先必须要验证计算结果.为了验证数值模拟的有效性，将计算结果与试验数据进行了对比.试验验证示意图如图2所示.

图2 试验验证示意图

在FFU的出口处设置了9个观测点，分别对比这9个点上的速度.x为水平方向长度，vn为速度，计算的结果可以用软件直接显示，采用热线风速仪进行测定得到试验结果，模拟结果和试验结果对比如图3所示，两者还是存在一定的误差，造成误差的原因主要包括数值仿真计算中的误差和测试中的误差.总体上两者数据吻合较好，误差在可接受的范围内，表明使用CFX来对FFU模型进行数值模拟得到的内部流场分布是可靠的.

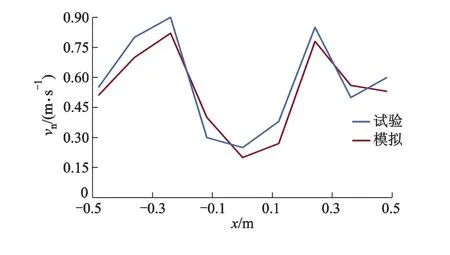
图3 模拟结果和试验结果对比图

3 结构参数优化

3.1 流道优化

为提高FFU的技术性能，降低阻力和噪声，在模型上对FFU进行优化设计.首先分析涡漩产生的原因，然后对模型进行适当的修改，再通过计算结果来判断优化后的效果，重复这一过程，直到达到最佳的效果.v为流速，S形流道出口处涡漩如图4所示.

图4 S形流道出口处涡漩图

S形流道突扩处的涡漩产生的原因是突扩结构处的流体产生了回流，被称为突扩回流.相关学者对影响回流的一些参数进行了广泛而深入的研究，普遍认为控制回流的主要因素包括:流动状态(层流、湍流)、初始速度分布、自由来流的湍流速度和突扩比等.由于流道面积的突然扩张，在面积变化的截面后存在回流、分离、重附和剪切等流动现象，会引起压力降低和能量损失，初始流道结构如图5所示.

图5 初始流道结构

因此对这一部分的优化主要集中在突扩结构的消除上，优化后的流道结构如图6所示，去除了这一突扩结构，流道几何形状缓慢变化.

图6 优化后的流道结构

修改成渐扩结构后，流道的截面积会逐渐增大，又由于流量是不变的，流速将逐渐变小，根据伯努利方程:

式中:z为高度;p为压力;ρ为流体密度;g为重力加速度;C为常数.

流道水平放置，故z不变，在速度v减小的情况下，压力p逐渐增大，因此随着流道的扩张，压力逐渐增大，在该区域内存在较大的压力梯度，流体从高压端流向低压端，流道出口区域会发生回流.

为解决这一问题，可以将流道截面积设计成相等，在流量一定的情况下，流道各处的流速相等，各处压力也趋于相等，不会出现大的压力梯度，就不会出现回流现象.等截面流道模型如图7所示.

图7 等截面流道模型

在流道逐渐扩张的过程中将高度逐渐减少，得到的精确方程为

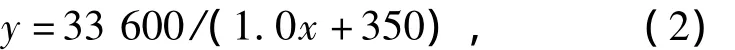
式中y为竖直方向长度.

按图7修改好模型之后再次进行计算，待计算收敛之后对结果进行分析，回流现象消失，所有的流体都同向运动，且十分流畅，达到优化的效果.优化后流道的整体速度矢量图如图8所示，涡漩全部消失，流动变得十分顺畅，有效减少流道阻力.

图8 优化后流道的整体速度矢量图

3.2 导流装置优化

FFU中导流板的作用是将S形流道流出的空气导入到下层空间，再经过过滤器进入室内，此过程中既要保证能量损失尽量小，又要保证送风的均匀性.因此导流板的弯曲角度和开孔数量及大小对送风状态有很大的影响.该型号的FFU的导流板弯曲角度为35°，笔者使用数值模拟的方法对比了弯曲角度分别为 20°，35°，50°这 3 种情况下的流动状态，得出了3种导流板形式下的流动状态的速度矢量图如图9所示.

图9 导流板角度在20°，35°，50°时的速度矢量图

单独观察图9a-c可以发现:在弯曲角度为20°时，左侧壁面附近区域有少量漩涡;弯曲角度为35°时左侧壁面附近出现漩涡;弯曲角度为50°时在导流板的正上方出现漩涡.

整体观察图9可以发现这种导流方式存在的几个典型问题:①无论怎么改变导流板的角度，均会出现气流回旋现象，表现在FFU的整体性能上就是在出风口的部分位置会出现出风不均匀现象;②导流板的切线方向上的速度远大于其他位置的速度，表现在出口速度上就是图3所示的双驼峰现象，导致出风极不均匀，出风均匀性是评价FFU的性能的一个最直观的指标，直接影响到室内的净化效率.出风的均匀性主要影响室内气流组织形式，GB 50457—2008《医药工业洁净厂房设计规范》规定100级以上的洁净室的气流流型应采用单向流，出风均匀性好的FFU能形成良好的单向流，不会在室内产生漩涡，减少污染物的堆积，净化效果明显提升;③都在左下角的直角转弯区域形成了一块流动速度很小的区域，该区域极易形成漩涡，导致能量的损失以及噪音的形成.综上所述，该导流板的作用不够理想，不能满足实际的要求，需重新设计导流板，重新设计的导流装置如图10所示，新的导流装置由2部分组成:① 一个环形的等截面的流道，能够将空气顺畅地导入到上层空间;②带条缝的导流板，导流板上的条缝数量及宽度由导流板上方的区域占整个出口区域面积的比例决定，以确保出口风量的均匀.另外导流板末端水平，流出的空气不会直接撞在过滤膜上，因此不会出现图3所示的双驼峰现象，出口速度将会比较均匀.修改后的导流矢量图如图11所示，导流板的导流效果非常明显，出风十分均匀.

图10 修改后的导流装置

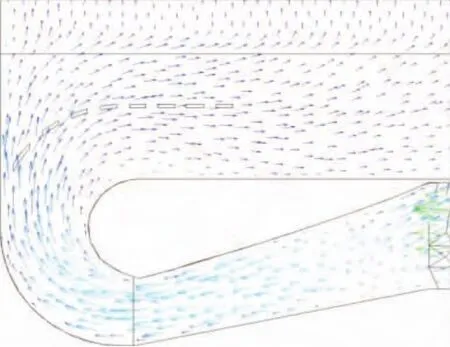
图11 修改后的导流矢量图

4 试验验证

为检验优化设计的合理性，将原FFU按上述的修改方案进行了修改，并用FFU性能测试台进行性能检测，FFU性能测试台如图12所示，可进行余压、定风量、定转速检测，依据GB/T 1236—2000《工业通风机用标准化风道进行性能试验》测试的性能参数包括风量、机外余压、转速、功率、空气动力效率、电压和电流等，同时得出完整的性能曲线.

图12 FFU性能测试台

为量化地评价出风的均匀性，将距离出口平面0.15 m处的平面上均匀布置27个测点，如图13所示，图中尺寸单位为mm.

图13 出口测点分布图

引入不均匀度作为评价指标.出风不均匀度为

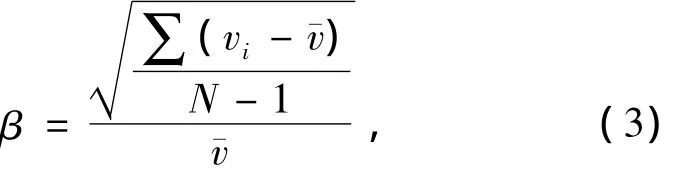
式中:vi为任一点实测风速;¯v为平均风速;N为测点数.

用式(3)表征出口速度的不均匀性，其值越大表示出风越不均匀.GB 50591—2010《洁净室施工及验收规范》中规定洁净室中气流不均匀度不大于25.00%.按照式(3)计算得优化前出风的不均匀度为23.84%，优化后出风的不均匀性达到19.63%，说明新的导流装置能有效提高出风的均匀性.

优化前后静压与面速度的关系如图14所示，在额定转速下变换风量得到不同静压值，优化后静压值有所提高，在面速度为0.45 m·s-1时静压提高了30 Pa左右，说明流道的改进提升了FFU的性能，可以应用在静压需求更高的场合，可以使用更高效的过滤膜.空气动力效率是指一定流量下推动空气流动的功率占总输入功率的百分比，表征了能量的有效利用程度.空气动力效率与面速度之间的关系如图15所示，由于高效过滤膜的阻碍作用，空气动力效率整体处于较低水平.空气动力效率的变化分为2个阶段:① 面速度较小时，优化前后的空气动力效率变化不大;② 当面速度大于0.4 m·s-1时，优化后的效率明显高于优化前，这是由于流道阻力与速度的平方成正比，随着速度的增大，流道的阻力变得越来越显著，此时阻力较小的流道空气动力效率更高.

图14 优化前后静压与面速度的关系

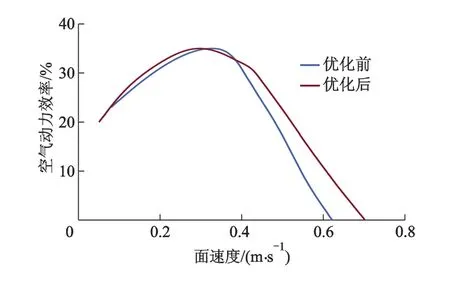
图15 优化前后空气动力效率与面速度的关系

5 结论

1)运用数值模拟的方法可以有效地模拟FFU的内部流场，并可以观察到FFU内部涡漩产生的具体区域.

2)通过对模拟结果的分析，修改了S形流道的突扩结构，并保证流道截面积相同，这样就可以消除突扩结构造成的涡漩，并且不产生回流现象.重新设计了导流装置，得到了更加均匀的出流.

3)使用FFU性能测试台对优化前后FFU性能进行对比，可以发现优化后的FFU出风更均匀，具有更高的静压，在风速较高时空气动力效率也更高.

References)

［1］徐玉党，沈晋明.室内污染控制与洁净技术［M］.重庆:重庆大学出版社，2006.

［2］洪玉忠.探讨FFU净化单元在生物制药洁净室的应用［J］.医药工程设计，2008，29(6):44-47.Hong Yuzhong.Discussion ofapplication ofFFU cleaned unit in cleaning room used in biological pharmacy［J］.Pharmaceutical＆Engineering Design，2008，29(6):44-47.(in Chinese)

［3］林忠平，肖小野，潘冬梅，等.风机过滤单元 (FFU)的性能试验研究［J］.建筑科学，2009，24(8):51-56.Lin Zhongping，Xiao Xiaoye，Pan Dongmei，et al.Experimental study on the performance of fan filter unit［J］.Building Science，2009，24(8):51-56.(in Chinese)

［4］Xu Tengfang，Jeng Mingshan.Laboratory evaluation of fan-filter units'aerodynamic and energy performance［J］.Journal of the IEST，2004，47(1):116-120.

［5］林忠平，肖小野.风机-过滤器单元结构组件对其性能影响的初步探讨［J］.暖通空调，2010，40(8):144-148.Lin Zhongping，Xiao Xiaoye.Preliminary study of fanfilter unit performance relating to the constituent components［J］.Heating Ventilating＆Air Conditioning，2010，40(8):144-148.(in Chinese)

［6］Liu Junjie，Tu Guangbei，Ma Jiuxian.Study on various rectifiers for fan-filter units［J］.Transactions of Tianjin University，2002，8(2):119-124.

［7］杨敏官，冯 浪，高 波，等.偏心搅拌槽内高浓度浆液颗粒的悬浮特性［J］.江苏大学学报:自然科学版，2012，33(6):643-648.Yang Minguan，Feng Lang，Gao Bo，et al.Particle suspension performance of high concentration solution in eccentric stirred tank［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(6):643-648.(in Chinese)

［8］田 飞，施卫东，张启华，等.2叶片潜水搅拌机叶轮内部流场特性［J］.江苏大学学报:自然科学版，2013，34(4):395-398.Tian Fei，Shi Weidong，Zhang Qihua，et al.Inner flow characteristics at impeller of submersible mixer with two blades［J］.Journal of Jiangsu University:Natural Science Edition，2013，34(4):395-398.(in Chinese)

［9］Keylock C J，Constantinescu G，Hardy R J.The application of computational fluid dynamics to natural river channels:eddy resolving versus mean flow approaches［J］.Geomorphology，2012，179:1-20.

［10］Miyake Y，Tsujimoto K，Beppu H.Direct numerical simulation of a turbulent flow in a channel having periodic pressure gradient［J］.International Journal of Heat and Fluid Flow，1995，16(5):333-340.

［11］Noh K C，Kim H S，Oh M D.Study on contamination control in a minienvironment inside clean room for yield enhancement based on particle concentration measurement and airflow CFD simulation［J］.Building and Environment，2010，45(4):825-831.

［12］Flaherty R.Clean rooms:continuing evolution of fan filter units for clean rooms［J］.Filtration and Separation，2011，48(4):33-37.

［13］Liu Hong，Li Peiwen.Even distribution/dividing of single-phase fluids by symmetric bifurcation of flow channels［J］.International Journal of Heat and Fluid Flow，2013，40:165-179.