扰动变系数组合KdV方程的同伦映射解

卢殿臣，陈婷婷，洪宝剑

(江苏大学非线性科学研究中心，江苏镇江212013)

同理可得式(12)在初始条件u2|t=0=0时的解:

对非线性偏微分方程(NPDE)的求解一直是数学物理工作者研究的重要课题，由于常系数的非线性发展方程只是在很多假设条件满足的情况下得到的一种理想形式，而变系数非线性发展方程能更准确地刻划众多的物理现象，因此研究其解有着重要的现实意义.近年来，国内外学者发展了许多求NPDE精确解及近似解的方法，如反散射方法［1］、齐次平衡方法［2］、椭圆函数方法［3］和摄动方法［4］等.同伦映射方法［5］是一种新的、普适性强的求解非线性偏微分方程的解析近似解的方法，被成功应用于解决工程技术中的许多非线性问题.如非线性振动［6］、边界层流动［7］等.笔者首先介绍同伦映射方法，并将该方法应用于研究扰动变系数组合KdV方程中，求其Jacobi椭圆函数形式的近似解，得到许多新的结果.

1 同伦映射法和椭圆函数形式解

现讨论如下扰动变系数组合KdV方程:

式中:a(t)，b(t)，c(t)为关于t的任意函数;f为关于其变量的充分光滑函数，f为扰动项.

方程(1)广泛应用于等离子体物理、固体物理、原子物理、流体力学和量子场理论等领域.如:当a(t)，b(t)，c(t)为常数，f=0 时，该方程转化为著名的组合KdV方程，在等离子体物理中它描述了无Laudau衰变小振幅离子声波的传播，在固体物理中用于解释通过氟化纳单晶的热脉冲传播，同时还可以很好地描述在具有非谐束缚粒子的一维非线性晶格中波的传播，又可作为流体力学中的一个模型方程;当f=R(t)时，方程(1)转化为强迫项组合KdV方程，文献［8-9］研究了其各种形式的精确解，如孤立波解、三角函数解、椭圆函数解等等;当b(t)=0时，文献［10］研究了其复合形式椭圆函数解.接下来笔者研究方程(1)的Jacobi椭圆函数形式的近似解.

为了方便起见，不妨令x=x'，t=t'，f(x，t，u，ux，ut)=f*(x'，t'，u，ux'，ut')，则式(2)化为

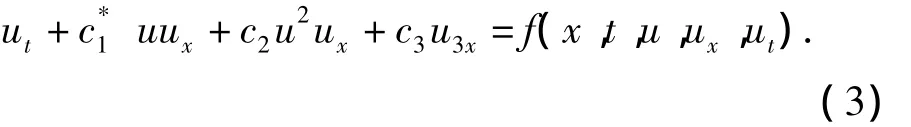
因此，研究式(1)的解转化为研究式(3)的解.为了得到方程(3)的近似解，引入同伦映射.

1.1 同伦映射法简介

假定给定了下面的非线性微分方程A(u)-f(r)=0，r∈Ω 及其边界条件B(u，∂u/∂n)=0，r∈Γ，式中A为一般微分算子;B为边界算子;f(r)为已知解析函数;Γ为区域Ω的边界.一般说来，算子A可分解为线性部分L及非线性部分N.所以方程A(u)-f(r)=0可写成L(u)+N(u)-f(r)=0.

现在建立同伦映射:H(u，p):Ω ×［0，1］→R，

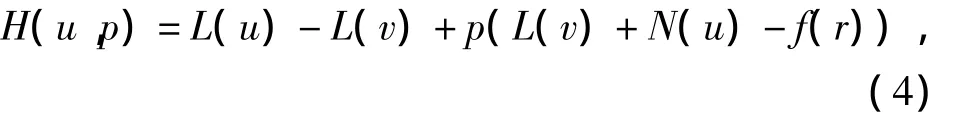
式中:p为参数;v为辅助函数，满足L(v)+N(v)=0.

由方程(4)得

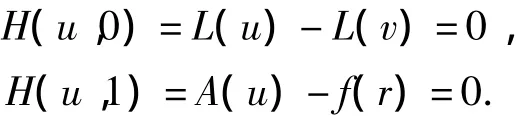
可以看出p从0变化到1的过程就是H(u，p)从L(u)-L(v)变化到A(u)-f(r)的过程，这就是同伦变形.令

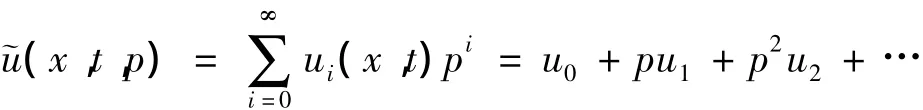
为H(u，p)=0的解.则当p=0时，˜u(x，t，0)=u0(x，t)是方程L(u)-L(v)=0的解;当p→1时，得到方程A(u)-f(r)=0的近似解u(x，t)=u0+u1+u2+….

1.2 椭圆函数形式解

针对方程(3)建立同伦映射H(u，p):R×I→R，R=(-∞，+∞)，I=［0，1］，有

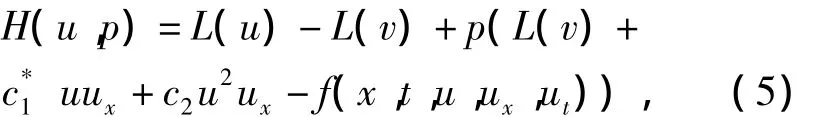
式中:v为辅助函数;L为线性算子，L(u)=ut+c3u3x.

借助广义椭圆法［11］，可以得到对应于方程(3)的典型组合KdV方程:

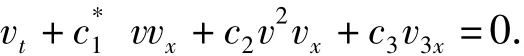
有下列椭圆函数形式解:

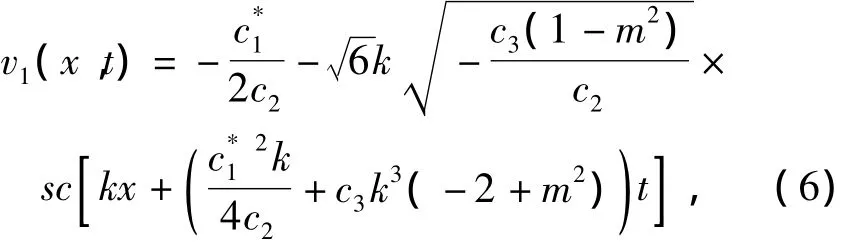
当m→1，退化为孤立波形式解:

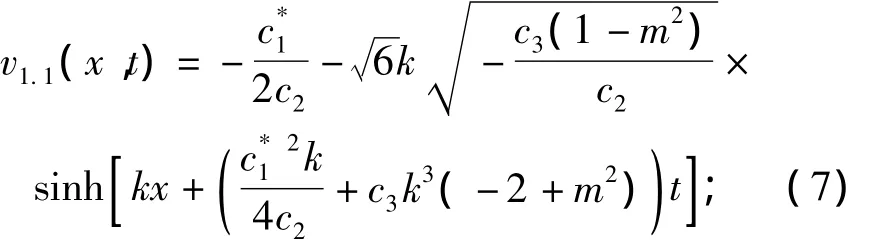
当m→0，退化为三角函数形式解:

式中:k为任意常数;m为模数且0≤m≤1.

易知H(u，1)=0与方程(3)相同，故方程(3)的解u(x，t)是H(u，p)=0的解当p→1的极限.令

由文献［12］可知，此级数在p∈［0，1］上是一致收敛的.

将式(9)代入方程H(u，p)=0中，取辅助函数v=v1(x，t)，对p的同次幂的系数进行比较:

由式(10)得u0(x，t)=v1(x，t).

由傅里叶变换可得式(11)在初始条件u1|t=0=0时的解:

同理可得式(12)在初始条件u2|t=0=0时的解:

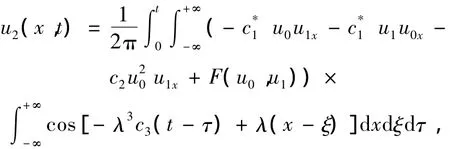
由此，可得方程(3)的椭圆函数形式二次近似解为

当m→1及m→0时，分别退化为下列近似解:

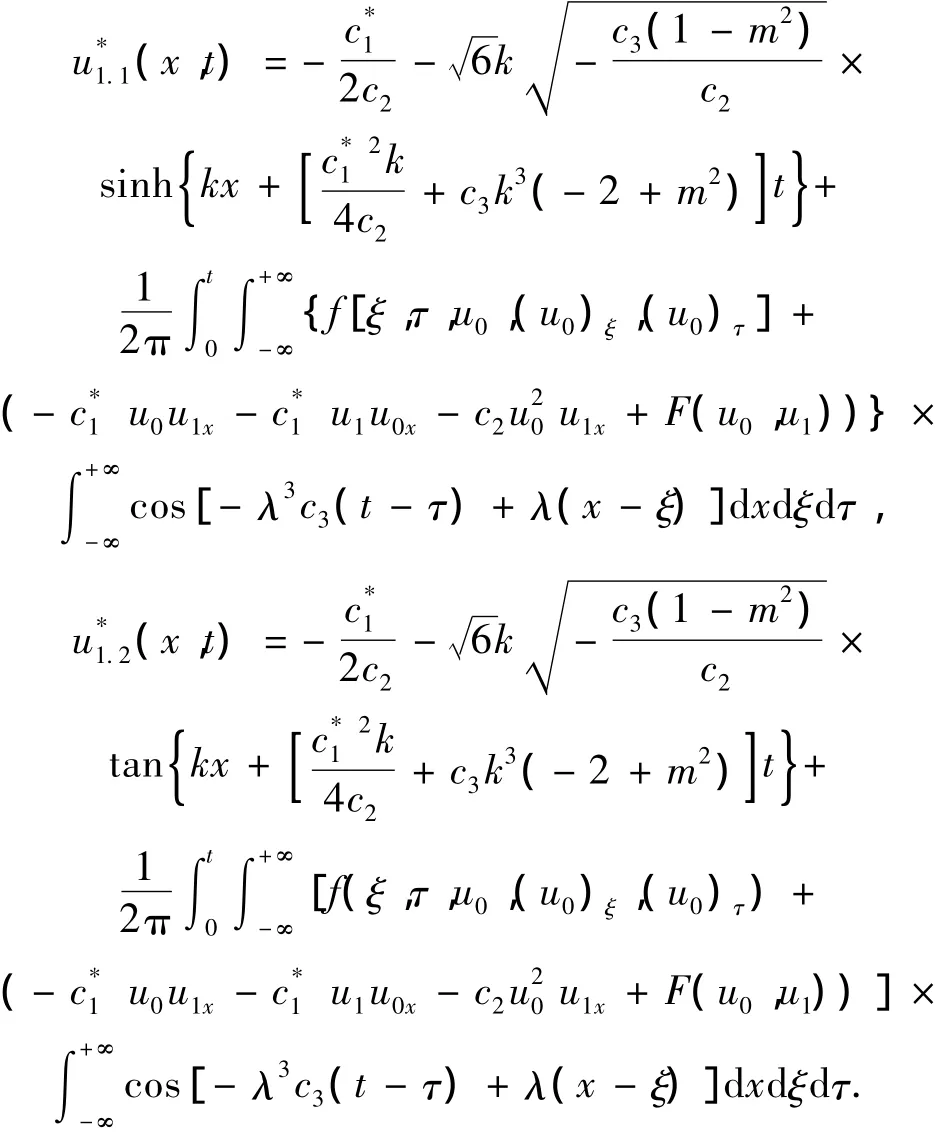
用同样的方法比较p的更高次幂的系数，还可以得到方程(1)的高次近似解.取不同的辅助函数，可以得到方程的不同形式的近似解.

2 微扰组合KdV方程的近似解

若方程(3)中的扰动项是微扰的，不妨设f=εun，其中ε为正的小参数，即方程(3)变为

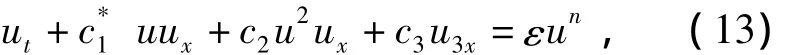
由上一节的结果可知方程(13)的椭圆函数形式近似解.其中零次近似解为u0(x，t)，一次近似解为u01(x，t)，二次近似解为u02(x，t)，则

3 结论

首次利用同伦映射法求解变系数组合扰动KdV方程，得到了具有Jacobi椭圆函数形式的二次近似解，在极限情形下可退化为双曲函数及三角函数形式近似解，并研究了其微扰情形下的近似解.同伦映射法可以应用于变系数孤子方程，具有简洁、高效的优点.

References)

［1］Ablowitz M J，Clarkson P A.Solitons，Nonlinear Evolution Equations and Inverse Scattering［M］.New York:Cambridge University Press，1991.

［2］Fan Engui.Two new applications of the homogeneous balance method ［J］.Physics Letters A，2000，265:353-358.

［3］Huang W H，Liu Y L.Jacobi elliptic function solutions of the Ablowitz-Ladik discrete non-linear Schrodinger system［J］.Chaos，Solitons and Fractals，2009，40:786-792.

［4］傅红笋，曹 莉，韩 波.测井约束地震波形反演的同伦摄动法［J］.地球物理学报，2004，55(9):2173-2179.Fu Hongsun，Cao Li，Han Bo.A homotopy perturbation method for well log constrained seismic waveform inversion［J］.Chinese Journal of Geophysics，2004，55(9):2173-2179.(in Chinese)

［5］石兰芳，周先春.一类扰动Burgers方程的孤子同伦映射解［J］.物理学报，2010，59(5):2915-2918.Shi Lanfang，Zhou Xianchun.Homotopic mapping solution of soliton for a class of disturbed Burgers equation［J］.Acta Physica Sinica，2010，59(5):2915-2918.(in Chinese)

［6］张琪昌，王 炜，何学军.研究强非线性振动系统同宿分岔问题的规范形方法［J］.物理学报，2008，57(9):5384-5389.Zhang Qichang，Wang Wei，He Xuejun.Homoclinic bifurcation of the strongly nonlinear oscillation system by the normal form method［J］.Acta Physica Sinica，2008，57(9):5384-5389.(in Chinese)

［7］李睿劬，李存标.平板边界层中湍流的发生与混沌动力学之间的联系［J］.物理学报，2002，51(8):1743-1749.Li Ruiqu，Li Cunbiao.A link between chaos dynamics and the onset of turbulence in a transitional boundary layer［J］.Acta Physica Sinica，2002，51(8):1743-1749.(in Chinese)

［8］卢殿臣，洪宝剑，田立新.带强迫项变系数组合KdV方程的显式精确解［J］.物理学报，2006，55(11):5617-5622.Lu Dianchen，Hong Baojian，Tian Lixin.Explicit and exact solutions to the variable coefficient combined KdV equation with forced term［J］.Acta Physica Sinica，2006，55(11):5617-5622.(in Chinese)

［9］套格图桑，斯仁道尔吉.辅助方程构造带强迫项变系数组合KdV方程的精确解［J］.物理学报，2008，57(3):1295-1300.Taogetusang，Sirendaoerji.The auxiliary equation for constructing the exact solution of the variable coefficient combined KdV equation with forcible term ［J］.Acta Physica Sinica，2008，57(3):1295-1300.(in Chinese)

［10］Sabry R，Zahran M A，Fan Engui.A new generalized expansion method and its application in finding explicit exact solutions for a generalized variable coefficients KdV equation［J］.Physics Letters A，2004，326:93-101.

［11］Hong Baojian.New Jacobi elliptic functions solutions for the variable-coefficient mKdV equation［J］.Applied Mathematics and Computation，2009，215(8):2908-2913.

［12］Liao S J.Beyond Perturbati on:Introduction to the Homotopy Analysis Method［M］.New York:CRC Press，2004.