基于ABM 与FBM 结合的精确快速相机自标定方法

李美燕，欧元汉

（广西大学 计算机与电子信息学院，广西 南宁530004）

0 引 言

运动获取结构［1］（structure from motion，SFM）是由运动的相机获取的多视图像集估计相机外部参数 （motion）并重建场景结构 （structure）的过程，它是计算机视觉领域中的一个核心问题。近年来，国内外在SFM 的研究上有很大的发展，已成功应用于大数据集的自动重建［2］。而计算机视觉与摄影测量在技术上相近［3］，许多研究尝试将SFM 流程引入到航空摄影测量中进行空中三角解算，以提高航测的自动化程度［4］。目前使用最广泛的SFM 方法是Bundler［5］，增量的绑定调整 （bundler adjustment，BA）主要用于完成互联网上非结构化图像的三维重建，而在恢复无人机航拍图像3D 点时，BA 产生的累积误差会导致特征点的重投影误差不均匀，中间的点误差较小，外围点误差却非常大，精度很难达到摄影测量规范的要求［6］。BA 的结果很大程度上取决于初始图像对的选择和后续图像的添加顺序，因此找到精确的匹配点和准确的tarcks信息对SFM结果的精确度有重要的影响。

传统SFM 使用SIFT［7］进行特征点的提取和匹配，许多文章验证了SIFT 能在原图提供很好的匹配结果，但它的运行时间较长，内存开销很大，因此在基于海量航拍图像的三维重建中很难实现可扩展性。分层匹配方法有效解决了这一问题，通常金字塔第n＋1层的图像分辨率比第n层的要低4倍，SIFT 运行时间要比第n层少，由此减少程序运行时间和内存开销，实现BA 的可扩展性。然而，如果仅仅在图像金字塔第三层 （或以上）执行SIFT 特征检测和匹配会出现大量匹配不准确或错配。杨化超等［8］提出的SIFT 改进算法在匹配相似灰度的图像时，正确匹配率得到了一定的提高，但该算法在原图执行SIFT 后仅使用NCC将一定阈值内的错配点剔除，并未修正错配特征点中心位置，也未能印证该匹配算法的可扩展性和对图像三维重建精确度的影响。Jose L.Lerma等［9］提出的自动定位和3D 建模方法最终得到较好的匹配结果和重建精度，但该方法未考虑旋转图像对归一化互相关匹配的影响，而无人机航拍过程中很容易受到风力等自然条件的影响导致图像存在旋转。孙卜郊等［10］改进的NCC匹配算法利用参考图进行多个角度旋转，以一定步长进行旋转搜索，从而达到匹配的目的，但是搜索的时间代价非常大不利于大数据的三维重建。

1 SFM 方法概述

SFM 为每张图像计算相机位姿和3D 点坐标。传统SFM 方法分为两个部分，第一部分为特征的提取和匹配，第二部分为相机位姿估计和3D 点坐标恢复。第一部分输入图像序列，然后对每张图像进行特征点的检测和匹配，使用检测到的匹配点进行基础矩阵F 和单应矩阵H 的估计；第二部分输入上一阶段得到的特征匹配对和相机内部参数，计算相对应的tracks，生成连通图G，依赖G 图依次估计相机外部参数并恢复特征点坐标，迭代执行BA 直至完成整个场景3D 点的恢复。

本文提出一种新的SFM 流程，将SIFT、NCC 和LSM相结合，目的是找到更精确的匹配对从而提高重建结果的精度。具体流程如下：在图像金字塔顶层使用SIFT 进行特征点的提取和匹配，减少时间和内存的开销，使程序更具可扩展性；将匹配结果作为NCC校正的初始匹配集，结合SIFT 的尺度和旋转信息对旋转图像进行局部矫正，然后逐层执行归一化互相关匹配，依次对错配点位置进行修正得到较精确的匹配对；最后使用最小二乘匹配将图像匹配的精度进一步提高到亚像素级甚至1／100个像素。修改特征文件中特征点的位置信息，估计基础矩阵F和单应矩阵H，从而改变tracks的计算和连通图G，最终提高三维重建的精度。同时，SIFT＋NCC＋LSM 的组合还可以分别设置阈值，作为一个过滤器，用来剔除误配点。

1.1 改进NCC匹配

SIFT 检测到特征点的三个信息——位置 （x），尺度（δ）和主方向 （θ）并生成特征描述向量，利用欧氏距离作为度量进行特征点的匹配，将匹配的特征点作为NCC 匹配的初始匹配点，缩小NCC匹配范围。归一化互相关方法通过计算模板窗口和搜索窗口之间的相关值来确定匹配的程度，当互相关系数值最大时搜索窗口的位置决定了模板窗口图像在待匹配图像中的位置。

NCC相关 系数定义如 下［11，12］

式（1）中：NCC（pi，qj）为 点 （pi，qj）处 的NCC 系 数，（2w＋1）× （2h＋1）为匹配模板的大小，I1（x，y）与I2（x，y）分别表示两图像 （x，y）处的灰度值，NCC 系数越大表示两幅图像越相似。

NCC互相关系数的分子本质上是代表灰度图的两个矩阵中对应各点的像素值两两相乘再求和。在没有旋转的情况下，它可以得到较好的结果，但是NCC 对旋转非常敏感，如果图像存在旋转NCC 将会面临以下问题：首先，同样大小的模板窗口与对应匹配点选取的搜索窗口覆盖的图像已经不同，像素相差有可能很大；其次，窗口中除了中心点 （即特征点）的像素之外，窗口内的像素不再存在一一对应关系 （如图1所示）；因此，NCC不适用于图像存在旋转的情况。而基于地面航拍图像的三维重建中，数据的采集是通过小型无人机按照一定的轨道拍摄所得。由于风力等自然条件的影响，小型无人机在航拍过程中会出现航线偏移或晃动，使得获取的图像存在旋转。因此在计算NCC系数之前要对图像进行局部校正。SIFT 特征点描述算子的过程中，将坐标轴旋转到关键点的主方向上，从而确保特征点的旋转不变性 （如图2所示）。因此，本文利用特征点主方向 （θ）将搜索模板做相对旋转校正以解决NCC不适用的情况。

图1 相关窗口

图2 sift特征点主方向

假设有匹配对 （pi，qj），其中特征点qj的主方向与特征点pi的主方向的相对夹角为β＝θi－θj，则图像旋转后坐标为

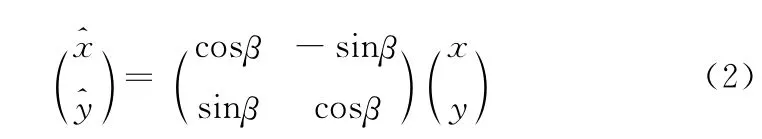
经过旋转校正后利用NCC算法的原理，将初始匹配点作为窗口的中心，待匹配的特征点从搜索窗口中心开始向四周移动，每次移动一个单位，遍历整个搜索窗口，分别求出 （2w＋1）× （2h＋1）个NCC 系数，NCC 系数最大时中心点位置为该匹配点的最终位置 （如图3所示）。如果该点为原初始匹配点的位置，则不对该特征点的位置信息做改变；否则修改特征点文件，将新的匹配点位置 （m＋x，n＋y）作为匹配点中心位置。

提高企业工作效能，增加利润，并不是只有与生产、销售等工作直接相关的人员和部门才负有的责任，企业应该从上到下树立一种效能思维，凡事都应该以提高工作效率，降低时间成本为目标进行。

图3 NCC遍历过程

1.2 LSM 匹配

无人机航拍采集图像时会受到光照、视角的影响，仅利用NCC对特征点位置进行初步调整不能得到完全精确的匹配位置，需要进一步对其进行精确调整。最小二乘匹配方法 （LSM）利用了图像窗口内的信息进行平差计算，可以将图像匹配的精度进一步提高到1／10 甚至1／100像素［13］。

对提取到的初始匹配点进行进一步匹配时，要为模板窗口与实际窗口引入变形系数，由于图像采集所使用的相机已标定，因此在只考虑几何畸变的情况下，将几何畸变看成是 仿射变换，即有［14，15］

式中：gl——实际窗口的灰度值，g2——模板窗口灰度值，h——线性系数，n1、n2——图像噪声，ai、bi（i＝0，l，2）为仿射变换的系数。上式经过线性变化后可得到误差方程如下

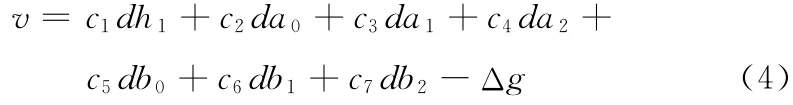
式中：ci（i＝1，...，7）为变形系数，Δg——窗口像素的灰度差。误差方程的系数为

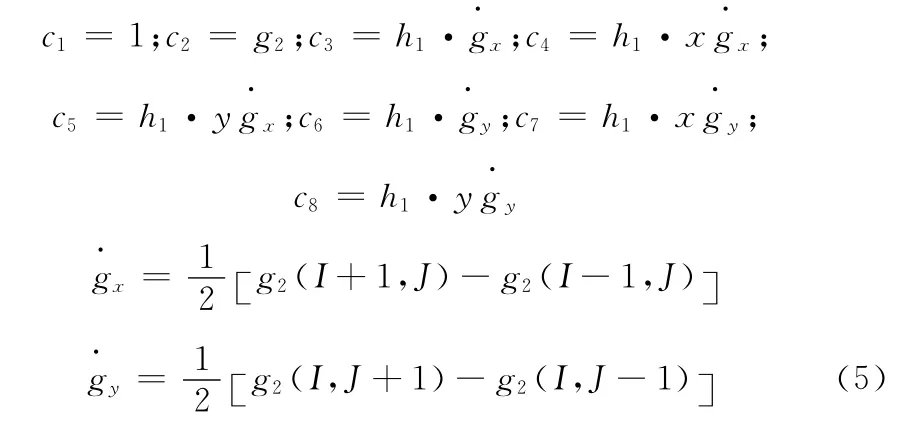
设未知数的初始值设为

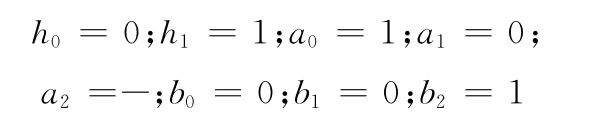
在窗口区域内逐像素建立误差方程，使用CTCX ＝CTΔG 解出几何变形系数。根据几何变形系数计算匹配点的最佳位置

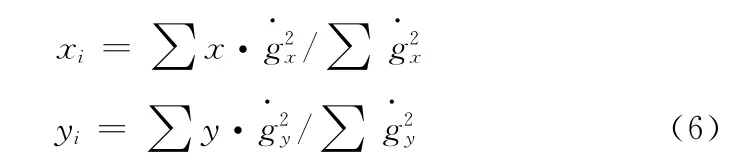
LSM 的过程可分为如下几步：①采用NCC 相关系数对初始匹配点进行修正，得到准确度较高的初始值，分别对图像的匹配点进行几何变形改正；②重复采样得到匹配点几何变形改正后的灰度值；③计算实际窗口与搜索窗口间的相关系数，判断是否符合迭代条件 （此处设置一个阈值，可用于剔除误配点）；④计算系统变形参数；⑤计算最佳匹配点位置。

2 实验与分析

本文选取一组210 张具高分辨率 （6000×4000）的无人机摄影图像作为实验数据，图像存在轻微的旋转，且拍摄场景均为无明显亮度变化的田地或存在地势高度差的山林。实验分为两部分：①在相似灰度的图像金字塔顶层提取高准确度的特征匹配点；②验证本文方法的重建精度；③验证SFM 新流程的可扩展性。

建立图像金字塔，在金字塔的第3层执行SIFT 特征提取和匹配，得到的部分匹配对如图4 （a）、（b）所示；从第2层到第0层逐层使用主方向对旋转图像进行局部校正，然后使用NCC对特征点坐标进行调整，调整后的匹配点位置如图4 （c）所示；最后在0层执行LSM 对匹配点的位置进一步修正，得到更为精确的匹配点，如图4 （d）所示。

图4 特征点匹配位置

从图4 （a）和图4 （b）可看出仅在顶层金字塔执行SIFT 会出现匹配不准确的情况；从图4 （c）可看出，使用主方向进行局部校正后再使用NCC对匹配点进行初步调整后匹配点中心位置得到改善，结果表明本文算法的解决了NCC不适用于旋转图像的问题；从图4 （d）看出匹配点经LSM 进一步修正后可得到精确的匹配位置。

为了测试本文算法的精确度，图5给出真实场景中的11个像控点的位置。设开源BA 算法恢复的像控点坐标和实际世界坐标的误差为 （Δx，Δy，Δz），本文算法恢复的像控点坐标和实际世界坐标的误差为 （Δx’，Δy’，Δz’），两误差之间的比较在图6显示。

图5 像控点位置

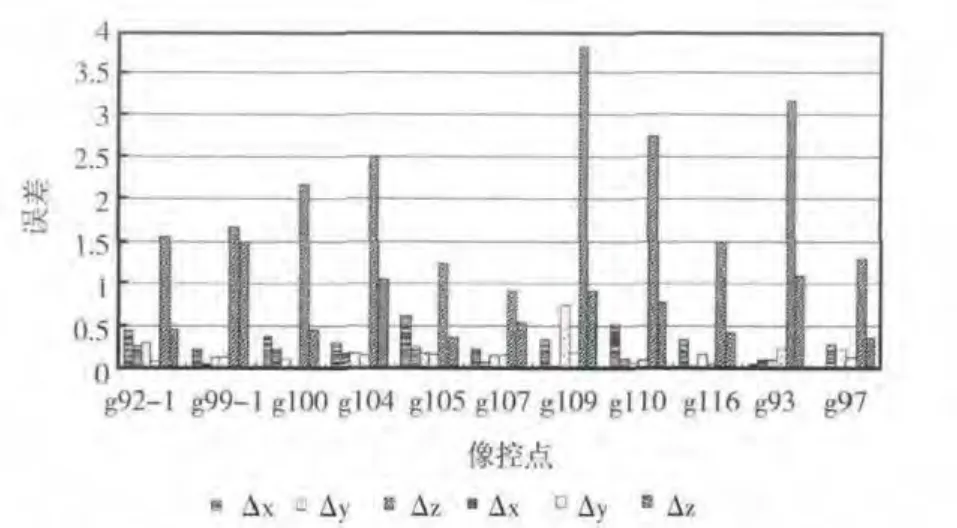
图6 改进算法与BA 回算3D 点的误差比较

从图6中可看出回算平面坐标 （x，y）时本文算法的误差略小于BA 的误差，但两者相差不大，误差都能保持在0.3～0.5之间，不能体现本文算法的优势。然而，在回算高程时本文算法体现了其高精确度。BA 回算的11个像控点的z坐标与像控点实际坐标相差都在1.5m 以上，最大的误差出现在g109这个点，达到3.8m，这已超出了实际测量的误差范围。而本文算法经绝对定向得到的高程误差能保持在1m 左右，其中有5个像控点的误差在0.5 m以内，只有g99－1这个像控点的误差达到1.5m。由此可验证本文算法在重建精度上优于BA，在实际的摄影测量中有较高的应用价值。

图7是3000张无人机航拍图像使用本文SFM 方法估计出的相机位姿和恢复的3D 点云，其重投影误差平均在0.5～0.7之间，运行时间为360min48s。实验表明本文方法具有可扩展性，能够自动、有效的处理海量数据，在海量数据航空摄影测量中有一定的实际应用价值。

图7 密集3D 点云

3 结束语

本文研究一种新的SFM 流程，使用分层匹配方法节省SIFT 特征点提取和匹配的时间和内存开销，使用特征点主方向对旋转图像进行处理，使NCC 适用于无人机航拍图像。采用改进后的NCC和LSM 依次对SIFT 初始匹配点的中心位置进行调整，有效的改善了匹配点的位置，提高匹配精度。利用这一匹配结果进行相机标定并回算3D 点坐标，为后续的三维重建提供高精确度的密集点云。实验结果表明，ABM 与FBM 结合的SFM 方法在基于无人机海量航拍图像的三维重建中具有高精确度和可扩展性，在摄影测量行业中具有一定的应用价值。

［1］Richard Szeliski.Computer vision：Algorithms and applications［M］.AI Haizhou，transl.Beijing：Tsinghua University Press，2012：265－273（in Chinese）.［Richard Szeliski.计算机视觉－－算法与应用［M］.艾海舟，译.北京：清华大学出版社，2012：265－273.］

［2］Sameer Agarwal，Yasutaka Furukawa，Noah Snavely.Building Rome in a day ［J］.Communications of the ACM，2011，54 （10）：105－112.

［3］ZHANG Zuxun.On informatization of surveying and mapping from the development of digital photogrammetry ［J］.Geomatics and Information Science of Wuhan University，2008，33（2）：111－115 （in Chinese）.［张祖勋.由数字摄影测量的发展谈信息化测绘 ［J］.武汉大学学报·信息科学版，2008，33 （2）：111－115.］

［4］Noah Snavely，Steven M Seitz，Richard Szeliski.Modeling the world from internet photo collections［J］.International Journal of Computer Vision，2008，80 （2）：189－210.

［5］Wu CC，Agarwal S，Curless B.Multicore bundle adjustment［C］／／Conference On Computer Vision And Pattern Recognition，2011：3057－3064.

［6］Steve Harwin，Arko Lucieer.Assessing the accuracy of georeferenced point clouds produced via multi－view stereopsis from unmanned aerial vehicle（UAV）imagery ［J］.Remote Sensing，2012，4 （6）：1573－1599.

［7］Sirmacek B，Unsalan C.Urban－area and building detection using SIFT keypoints and graph theory ［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，47 （4）：1156－1167.

［8］YANG Huachao，ZHANG Shubi，ZHANG Qiuzhao.Least squares matching methods for wide base－line stereo images based on SIFT features［J］.Acta Geodaetica et Cartographica Sinica，2010，39 （2）：187－194 （in Chinese）. ［杨化超，张书毕，张秋昭.基于SIFT 的宽基线立体影像最小二乘匹配方法 ［J］.测绘学报，2010，39 （2）：187－194.］

［9］Jose L Lerma，Santiago Navarro，Miriam Cabrelles，et al.Automatic orientation and 3D modelling from markerless rock art imagery ［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2013，76：64－75.

［10］SUN Bojiao，ZHOU Donghua.Rotated image registration method based on NCC ［J］.Transducer and Microsystem Technologies，2008，27 （5）：43－45 （in Chinese）. ［孙 卜郊，周东华.基于NCC 的存在旋转的图像匹配方法 ［J］.传感器与微系统，2008，27 （5）：43－45.］

［11］HUANG Zhenbao，CHEN Yang.A fast method for NCC algorithm in image matching ［J］.Informatization Research，2011，37 （2）：48－52 （in Chinese）. ［黄真宝，陈阳.图像匹配中NCC 算法的一种快速实现方法 ［J］.信息化研究，2011，37 （2）：48－52.］

［12］WANG Wantong，LIU Pengfei，HAN Zhigang.Multi－sensor image registration method based on SIFT and NCC algorithm［J］.Computer Engineering and Applications，2012，48（3）：10－12 （in Chinese）.［王万同，刘鹏飞，韩志刚.基于SIFT 和NCC的多源遥感影像配准方法 ［J］.算机工程与应用，2012，48 （3）：10－12.］

［13］ZHOU Shilun.The research and realization of the least squares image matching algorithm ［J］.Information ＆Communication，2013，27 （4）：35－36 （in Chinese）. ［周时伦.最小二乘影像匹配算法的实现与研究 ［J］.信息通信，2013，27 （4）：35－36.］

［14］ZHU Zunshang，ZHU Zhaokun，CHEN Shengyi，et al.An adaptive window affine least squares matching method ［J］.Journal of National University of Defense Technology，2013，35 （4）：46－50 （in Chinese）. ［朱遵尚，朱肇昆，陈圣义，等.自适应窗口仿射最小二乘匹配方法 ［J］.国防科技大学学报，2013，35 （4）：46－50.］

［15］KOU Rong.Study on the correlation coefficient and the least square image matching algorithm ［J］.Inner Mongolia Science Technology ＆ Economy，2010 （17）：60－63 （in Chinese）.［寇蓉.相关系数与最小二乘影像匹配算法的研究 ［J］.内蒙古科技与经济，2010 （17）：60－63.］