基于AETG 算法的两两组合测试用例生成方法

梁 凡，宋晓秋

（中国航天科工集团第二研究院706所，北京100039）

0 引 言

在软件的测试工作中，常常会遇到某些软件失效是由多个参数互相作用引发的情况。事实上，大约70%的软件失效是由一个或2个参数作用引起的［1］。因此两两组合测试就成为了软件测试中一种实施性较强同时又比较有效的方法［2］。但是对于一个由K 个参数构成的系统，每个参数的取值为V ［i］（i＝1，2……k），要覆盖所有可能的参数取值组合，就需要个测试用例［3］，显然这个测试用例的规模不符合实际。所以，如何取得一个能覆盖所有配对的最小的测试用例集就成为两两组合测试研究中最重要的问题［4］。但是，研究结果表明生成这样一个最小的测试用例集是一个NPC 问题，即不存在多项式时间的解法［5］，所以研究的目标就成为寻找一个尽可能小的测试用例集去覆盖所有可能的配对。

1 两两组合测试算法简介

1.1 正交拉丁算法简介

早在1985年，就已经有学者提出了正交拉丁算法［6］，将正交拉丁方的特性用于生成多元输入情况下的测试用例。但是在实际工作中，大部分的待测系统都不能满足拉丁方的数学特性，导致正交表构造困难，从而很难生成理想的测试用例集。近些年来，许多学者以正交拉丁算法为基础，提出了一些改进的算法。比较有代表性的有加拿大渥太华大学的A.W.Williams提出的Williams算法，日本的Noritaka Kobayashi提出的Kobayashi算法等［7］。这些算法存在相同的问题，即构思巧妙，但是实用性不强。

1.2 AETG 算法简介

1997年，贝尔实验室的Cohen和Dalal提出了AETG方法，算法的主要思想是首先按贪心算法生成一定数量N个测试用例，然后从这N 个测试用例中选择一个能最多覆盖未覆盖配对集合中参数对的用例，将这个用例添加进已经形成的测试用例集T 中［8］。从算法的执行过程不难发现，每次产生的N 个待选择测试用例的差别造成了算法结果的差别。所以这也是AETG 算法能进行改进的主要部分。

1.3 IPO 算法简介

1998年，北卡罗来纳大学的Y.Lei和K.C.Tai提出了一种基于参数顺序的渐进扩充的两两配对组合测试用例生成方法IPO （in－parameter－order）［9］。算 法 首 先 以 参 数 为 对象，生成配对覆盖所有可能的组合测试集T，这个过程称为水平扩展。然后逐个向测试集中添加参数，并通过扩展算法覆盖这个参数和当前测试集T 内每个参数所能够形成的所有组合，并使测试集保持最小，直到所有的参数都添加到测试集里，这个过程称为垂直扩展。

1.4 各种算法比较

正交拉丁算法以及所有以正交拉丁算法为基础的算法存在共同的缺陷，即对于能够构造正交表的待测系统而言，算法简单有效，但是大部分的待测系统不能满足这样的要求，这就使得这类算法存在适应面窄的问题［10］。AETG 算法每次生成一个测试用例的时候都能在当前可选择的范围里选择那个能覆盖最多未覆盖配对的用例，但是一次生成很多条测试用例待选择，不断地遍历未被覆盖的配对集合，使得AETG 算法的时间开销大大增加［11］。而IPO 算法每次生成一个测试用例，这个测试用例保证能添加进测试用例集，使得每次遍历的效率很高。但是从覆盖尽可能多的配对的角度看，一次生成一个测试用例明显不如一次生成一些测试用例然后选取最优的那个用例［12］。所以，AETG 算法最大的优点是能得到更小的测试用例集而IPO 算法最大的优点是能花费更少的时间。

当今的硬件水平下，执行用例生成算法的时间是微不足道的。实验结果表明，对于一个由100 个参数，每个参数有4个取值组成的待测系统而言，在普通家用电脑上利用AETG 算法生成测试用例集需要花费大约260s的时间。这个时间与测试人员进行一个用例的输入，测试与分析所需要花费的时间对比起来，是微不足道的。所以，如何在合理的时间内得到尽可能小的测试用例集就成了组合测试问题上最需要解决的问题。

综上所述，从实际工程应用的角度来考虑，AETG 算法比IPO 算法更加实用。下面给出一种改进的AETG 算法，称为AETG＿I算法 （AETG improved）。

2 基于AETG 算法的改进方法

2.1 AETG 算法描述：

如果测试用例集T 中已经包含了用例t1，t2……ti，下面给出生成ti＋1的方法：

（1）首先选取一个参数Fi，且Fi的值Vfi在未覆盖配对集合UC （uncovered）中出现的次数最多。

（2）令F1＝Fi，然后对剩余的参数任意排序，得到任意的F2，F3……Fn。

（3）对于任意排序得到的参数，按顺序选择其参数值，如果本次应选取的参数是Fi，则计算Fi的所有参数值，选择与已形成的F1，F2……Fi－1的各个值构成的配对在UC中出现最多的那个参数值，将其添加进已形成的参数组中，接着再用相同的方法扩展Fi＋1。

重复以上3个步骤N 次，其中N 为某个人为设定的数量，产生N 个待选择的测试用例。

当已经得到N 个测试用例之后，从这N 个测试用例中选择能覆盖UC 中最多未被覆盖的配对的那条用例，并将其添加进T。

看起来，当N 越大的时候每次选取的那个测试用例就越能接近最优解，但是N 值过大会极大地增加算法所需要的时间和空间开销。针对这个问题，Cohen和Dalal做了很多次实验发现N＝50的时候，N 值的继续增大并没有明显的减少测试用例集的大小，所以可以取N＝50。

观察AETG 执行的过程不难发现，算法的第2步，即任意排序得到待扩展的参数序列随机性很大，而这种随机性很容易冗余。举一个例子：某个待测系统有4 个参数，AETG 方法进行到某步时，UC＝ ｛（A1，D1），（A1，B1），（A1，D2）， （B1，D1）， （A1，B2）， （D1，C2）， （A2，C2）｝，按照AETG 方法，首先扩展A1，如果随机形成的参数扩展顺序为ACDB，则生成的测试用例为 （A1，C1，D1，B1），覆盖了UC中3个配对 （A1，D1），（B1，D1），（A1，B1）。但是如果测试用例为 （A1，D1，B1，C2）则可以覆盖UC中4 个配对 （A1，D1）， （A1，B1）， （B1，D1），（C2，D1）。这种差异主要是由AETG 方法随机排列参数的自由性所带来的。虽然AETG 方法要将这个生成测试用例的步骤执行50次，可以在很大程度上减少因为这种参数顺序的不确定性带来的影响。但是如果一个系统有6个或以上的参数，除去已经选择的F1，剩余参数的全排列有远远大于50种可能性。所以如何有效的改善第2个步骤就成为优化AETG 算法的关键。

2.2 AETG 算法的改进

改进的AETG 算法 （AETG improved，AETG＿I算法）主要思想是让每个参数的选择均采用与第1个参数相似的方法，即按照参数在UC 中出现的次数差异决定参数的选择顺序。同时对于出现次数相同的那些参数，根据其某些特点赋予不同的优先级，决定其排列顺序。具体改进分为两部分。

2.2.1 AETG＿I算法改进的第1部分

（1）首先选取一个参数Fi，且Fi的值Vfi在未覆盖配对集合UC中出现的次数最多。

（2）令F1＝Fi，然后对剩余的参数按照其V 在UC 中出现的次数的不同，得到按Vi出现次数排序后的F2，F3……Fn。

但是在实际的测试用例生成过程中，可能存在某2个或某些参数其值在UC 中出现的次数相同。例如如果一个待测系统共有10个参数，每个参数有2个取值，如果第1个生成的测试用例是 （A1，B1，C1，D1，E1，F1，G1，H1，I1，J1）。当生成第2个测试用例时每个参数在UC 中出现的次数都是一样的。发生这种情况时，需要让每个取值个数相同的参数都能在相同重要的位置出现一次。所以，在选择排序的时候，需要再增加约束条件。例如：UC＝｛（A3，B2），（A2，B2），（A1，B3），（A1，B4），（B3，C2），（A1，C2），（A1，D2）， （B2，C2）｝，如果按照目前的选择方法，首选A 或B，如果首选B，第1次生成的测试用例为（B2，A2，C2，D2）覆盖了UC 中的配对为 ｛（A2，B2），（B2，C2）｝，如果首选A，则生成的测试用例为 （A1，B3，C2，D2）覆盖了UC 中的配对为 ｛（A1，B3），（B3，C2），（A1，C1），（A1，D2）｝。显然选择第1次扩展A 更加合适，这主要是因为参数A 中的A1在UC中出现的次数占据绝对优势。所以当有2个或更多的参数其值在UC 中出现的次数相同时，应该优先选择包含某个出现次数绝对多的取值的那个参数。

下面举例说明这种选择的方法：

如果某个待测系统有5个参数A，B，C，D，E，每个参数各有2种取值。当前的UC是 ｛（A1，B2），（A2，B2）（A1，C2），（A1，D1），（A1，D2），（A1，E2），（B1，C2），（B2，D1），（B2，D2），（B1，E2），（C1，D2），（C2，D1），（C2，E1）｝。观察UC，其中A1出现5 次，A2出现1 次。B1出 现2次，B2出 现4 次。C1出 现1 次，C2出 现4 次。D1出 现3次，D2出 现3 次。E1出 现1 次，E2出 现2 次。其中A，B，D 这3个参数在UC 中出现的次数相同都是6次，但是A1出现了5次，B2出现了4次，D1和D2都是出现了3次。所以第1次生成的参数排序为：A，B，D，C，E。然而需要将A，B，D 在相同重要的位置都出现一次，但是这3个参数本身按照其出现次数最多的取值个数不同而本身存在选择上的重要性差距。所以还需要生成参数顺序为：B，A，D，C，E和D，A，B，C，E。

综上，改进的第 （2）步描述为：

如果参数X，Y，Z 在UC 中出现的次数相同，且｜Xi｜＞｜Yj｜＞｜Zk｜ （｜Xi｜表示Xi在UC 中出现的次数）。则应该优先选择Xi进行扩展。为了保证每个在UC中出现次数相同的参数都能在同样重要的位置出现一次，同时需要兼顾每个参数由于出现次数最多的取值所带来的优先级问题。即每次优先选择一个参数进行扩展，但是剩余参数必须保证按出现次数最多的那个取值的数量排序，需要生成 （＿， ＿，...，X，Y，Z， ＿...）， （＿， ＿，...，Y，X，Z， ＿...），（＿， ＿，...，Z，X，Y， ＿...）。同样的，在之后的每一步操作中如果存在2个或多于2个的参数在UC中出现的次数相同时，都选择同样的方法。

（3）第3步与原方法大致相同，但是原AETG 方法在进行参数值选择时采用的是向前对比的方法，这种方法存在一个问题，例如某个待测系统有4 个参数，每个参数有3个取值，生成某个测试用例时参数扩展顺序定为ABCD，且 首 先 选 取 了A1，那 么 如 果 （A1，B1），（A1，B2），（A1，B3）在UC 中都存在，这时如何选取B的取值就存在很大的问题。所以将第3步修改为向前，向上对比。即此时对比B1，B2，B3在UC 中出现的次数，如果B1出现5次，B2出现4 次，B3出现6 次，选择B3加入。

AETG＿I算法的第3步可以描述为，优先选择与前面参数能覆盖最多UC 中的配对的那个参数值加入，如果存在某几个参数值与前面的取值组成的配对在UC 中出现的次数相同，则优先选取在UC 中出现次数最多的那个参数值加入。

2.2.2 AETG＿I算法改进的第2部分

在最初的AETG 方法中，需要生成50个待选择的参数序列。在改进的方法中，将参数排序后避免了原来方法的盲目性，也就可以适当的减少操作进行的次数。如果｜A｜＝｜B｜＝｜C｜，｜G｜＝｜H｜＝｜J｜＝｜K｜，那么在进行参数选择的时候，A，B，C 需要出现在相同的位置，那就至少需要3 次，G，H，J，K 至少需要4 次，则在这种情况下就至少需要12个测试用例。在用例形成的开始阶段，各个参数的不同取值使用程度相差不大，这时就会导致测试用例的数量可能会随着参数数量的增加或者取值的增加远远大于50，而进行的几组实验证明，将生成的测试用例数量上限定义为50已经可以得到非常理想的结果。所以当计算出来的重复步骤大于50 时使用传统的AETG 方法，即将第1部分第2步生成的参数序列上限设为50，当用例集形成后期，各个参数之间差别较大，测试用例数量很难超过50。

所以AETG＿I算法的第2部分即迭代次数定义为：

如果在UC中存在与｜X｜出现次数相同的参数n1个，与｜Y｜相同的n2个……与｜Z｜相同的ni个。则需要的迭代次数为N＝n1×n2×……×ni次。如果N≥50，则迭代50次，如果N≤50，则迭代N 次。

2.3 改进的AETG 算法描述

下面给出改进的AETG 算法的算法描述，如图1所示。

2.4 AETG＿I算法分析

2.4.1 间复杂度分析

因为改进后的方法迭代次数在用例生成工作的后期会越来越小，所以新方法在时间复杂度上根据待测系统的不同会不同程度的小于原AETG 方法。尤其是当参数的取值每个之间都存在差异，也就是参数取值情况参差不齐的时候，算法能很容易的找到每次待扩展的参数顺序，而不是像传统的AETG 方法那样必须取50种排序，这种情况下就更能缩短算法需要的时间。

图1 AETG＿I算法描述

对于任意一个有K 个参数的待测系统而言，符合两两组合测试条件的测试用例集规模上界为－log（k（k－1）d2／2）／log（1－1／d2）＋1 ，其中 （d＝max （V ［i］，i＝1，2…k），V ［i］为每个参数的取值个数）［13］。每条用例包含的配对数为k× （k－1）／2，每确定一个参数取值平均需要遍历UC的次数为k／2次，UC的大小为d2×k× （k－1）／2。对于传统的AETG 算法来讲，当参数数量超过6（5！＝120）时，AETG 算法每一次都必须取到50 个测试用例。所以AETG 算法的时间复杂度上限为

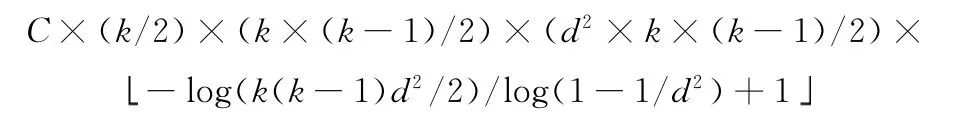
其中当k≥6时，C＝50。但是对于AETG＿I算法，C 上限为50，下面给出一组实验说明，实验输入参数为13个，每个参数取值为3个。

AETG＿I算法与AETG 算法复杂度比较见表1。

从上述实验可以看到，对于AETG＿I算法，随着已经生成的测试用例数不断地增加，其每确定一个测试用例所需要生成的带选择用例数就会越来越少。对比AETG 算法每次都需要生成50 个待选择测试用例，AETG＿I算法在时间复杂度上确定得到了很大的改进。

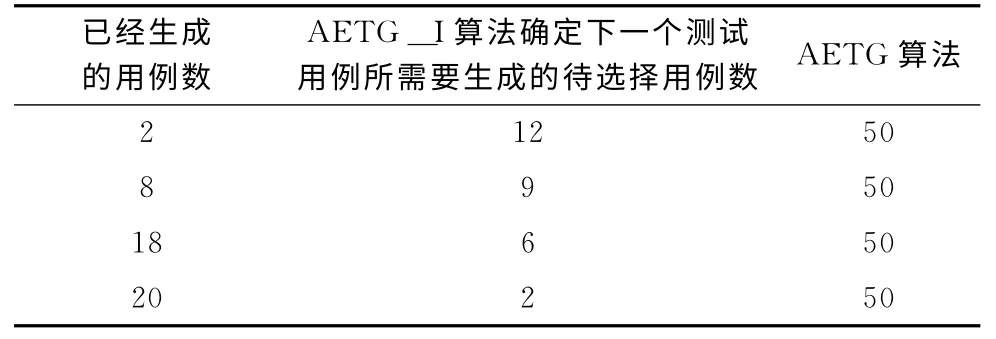
表1 AETG＿I算法与AETG 算法复杂度比较

2.4.2 结果分析

下面选取几组实验对比改进后的算法与原AETG 算法，见表2。

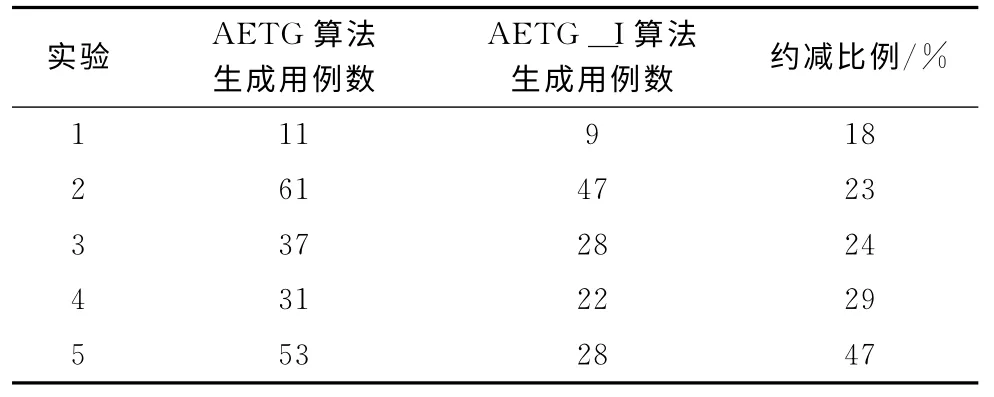
表2 AETG＿I算法与AETG 算法结果对比

其中：

实验方案1：4个参数，每个参数都是3个取值。

实验方案2：5个参数，每个参数都是6个取值。

实验方案3：8个参数，其中2 个参数是3 个取值，2个参数是5个取值，3个参数是4个取值，1个参数是2个取值。

实验方案4：13个参数，每个参数都是3个取值。

实验方案5：21个参数，其中5个参数是2个取值，4个参数是4个取值，1个参数是5个取值，6个参数是3个取值，5个参数是3个取值。

观察以上实验情况，改进后的AETG 方法对比原方法在生成用例集的大小上也有很大的改进。而且观察不同参数选择情况可以发现，当参数的数量越来越多时，新的AETG 方法更能体现其优越性。

3 结束语

传统的AETG 算法弊端比较明显，即参数选取的过程随机性很大。将迭代次数定为50对于一些小型的待测系统而言，能够取得不错的结果。但是现在随着软件系统的日益庞大，输入参数的数量和取值也随着越来越多。在实际的测试工作中，执行与分析一个测试用例的人员开销要远远比生成测试用例所需要的时间宝贵。所以，如何能在一个合理的时间内得到尽可能小的两两组合测试用例集才是组合测试问题的瓶颈。本文针对AETG 算法的这个缺陷进行了改进，将原来无序的参数选择过程改为按照参数未被覆盖的取值个数综合起来决定参数的选择顺序。并进行了几组实验验证了改进的算法确实能够大幅度减少测试用例集的规模，尤其是当参数的取值逐渐增加时，改进后的算法优势更加明显。当然，完成两两组合测试用例集的生成只是组合测试工作的第1步，如何快速的定位导致软件失效的配对，以及更多元的配对组合测试用例集生成问题仍然是今后需要重点研究的方向。

［1］Maity S，Nayak A.Improved test generation algorithms for pair－wise testing ［C］／／16th IEEE International Symposium on Software Reliability Engineering，2005：235－244.

［2］ZHA Rijun，ZHANG Deping，NIE Changhai，et al.Test data generation algorithm of combinatorial testing and comparison based on cross－entropy and particle swarm optimization method［J］.Chinese Journal of Computers，2010，33 （10）：1896－1908 （in Chinese）. ［査日军，张德平，聂长海，等.组合测试数据生成的交叉熵与粒子群算法及比较 ［J］.计算机学报，2010，33 （10）：1896－1908.］

［3］YAN Jun，ZHANG Jian.Combinatorial testing：Principles and methods［J］.Journal of Software，2009，20 （6）：1393－1405 （in Chinese）. ［严俊，张健.组合测试：原理与方法［J］.软件学报，2009，20 （6）：1393－1405.］

［4］Myra B Cohen，Matthew B Dwyer，Shi Jiangfan.Constructing interaction test suites for highly－configurable systems in the presence of constraints：A greedy approach ［J］.IEEE Transactions on Software Engineering，2008，34 （5）：633－650.

［5］WU Yanjie.Research and implementation of algorithm for pairwise testing ［D］.Wuhan：Huazhong University of Science and Technology，2008 （in Chinese）.［吴彦杰.多元配对组合测试的算法研究与实现 ［D］.武汉：华中科技大学，2008.］

［6］White LJ.Regression testing of GUI Event interactions［C］／／The International Conference on Software Maintenance，2007：350－358.

［7］ZHOU Wujie，ZHANG Deping，XU Baowen.An adaptive algorithm of locating fault interactions based combinatorial testing［J］.Chinese Journal of Computers，2011，34 （8）：1509－1516 （in Chinese）. ［周吴杰，张德平，徐宝文.基于组合测试的软件故障定位的自适应算法 ［J］.计算机学报，2011，34（8）：1509－1516.］

［8］CHEN Xiang，GU Qing，WANG Xinping，et al.Research advances in interaction testing ［J］.Computer Science，2010，37 （3）：1－5 （in Chinese）.［陈翔，顾庆，王新平，等.组合测试研究进展 ［J］.计算机科学，2010，37 （3）：1－5.］

［9］Colboum CJ，Cohen MB，Bryce RC.A deterministic density algorithm for pairwise interaction［C］／／Proceeding of the International Conference on Software Engineering，2004：345－352.

［10］HUANG Long，YANG Yuhang，LI Hu.Research on algorithm of parameter pairwise and n－way combinatorial coverage［J］.Chinese Journal of Computers，2012，35 （2）：257－268（in Chinese）.［黄陇，杨宇航，李虎.参数配对及n－way组合 覆 盖 算 法 研 究 ［J］.计 算 机 学 报，2012，35 （2）：257－268.］

［11］Ren Zhengping，Huang Song，Wan Hui，et al.Research on testing technology of command and control information system［C］／／16th Information－based Theory Science－Workshop，2009.

［12］Hui Zhanwei，Huang Song，Su Shihan，et al.Research on generation methods of pair－wise covering combinatorial test cases［C］／／Asia－Pacific Conference on Information Theory，2010：264－267.

［13］Zhu Xiaojun.Research and implementation of software testing method based on parameter pairwise combination ［D］.Shanghai：Shanghai Normal University，2004.