对多混沌映射图像加密算法的分析与改进
2014-12-23刘祝华
刘祝华,袁 文
(江西师范大学 物理与通信电子学院,江西 南昌330022)
0 引 言
近年来,图像加密技术越来越重要,学者设计出了众多图像加密算法[1],而混沌系统由于其对初始条件和参数的敏感性及类噪声特性,被广泛应用到数字图像加密算法设计中[2]。基于低维混沌的图像加密算法具有混沌序列计算简单的优点,但计算机的有限精度会使混沌序列出现短周期的问题,且密钥空间较小,导致算法的安全性不高[3-6]。与低维混沌相比,高维混沌具有更加复杂的动力学行为和更好的随机性,因此,许多研究者提出了各种基于超混沌的图像加密算法[7,8],但高维混沌系统计算的复杂性却限制了其在实时环境下的应用。采用多个低维混沌相复合构建加密算法,可以避免高维混沌计算复杂的问题,同时又可以解决低维混沌动力学特性简单和密钥空间小的问题[9],因此,越来越受到研究者的关注[10-14]。
郭晓丛等[10]提出了一种基于多混沌映射的图像加密算法,采用3个低维混沌映射生成3个与图像大小相等的混沌序列,视作空间中某点的坐标,再按空间直角坐标系中2点的距离公式,求解与图像对应像素点坐标值的距离,并作为加密因子。该算法生成加密因子的思路比较新颖,且采用多混沌映射,密钥空间大,但也存在安全隐患。本文分析了该算法存在的缺陷,并在安全性上给出了改进措施,提出了一种自适应多混沌分块图像加密算法。理论分析与实验结果表明,改进算法安全性高,且加密速度快。
1 原算法分析
1.1 原算法设计思路概述
对于M×N 的图像I,由二维Logistic映射生成2个长度为M×N 的混沌序列,并取小数点后13至15位,对256取模,得序列X1、Y1,由X1、Y1异或得序列L1。以相同的方法,由Hénon 映射生成序列L2,由Ikeda 映射生成序列L3。
把L1、L2和L3视作空间上点P 的坐标,则P 点的坐标为P(x,y,z),其中x ∈L1,y ∈L2,z∈L3。把图像I看成同一平面内的M×N 个质点,每个质点的坐标为Q(i,j,0),其中i∈[1,M],j∈[1,N]。由空间中两点距离平方公式生成加密因子
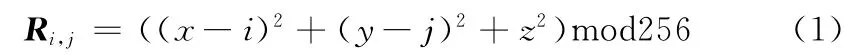
式中:mod为取模运算。
原图像I向左循环移动一列,向上循环移动一行得Icr,并和加密因子异或得到密文图像Bi,j=Icri,j⊕Ri,j。
1.2 原算法设计缺陷
首先,对于大小为M×N 的图像I,每个像素点的坐标值(i,j)是固定的。因此,加密因子Ri,j只与混沌映射的参数及初始值有关,因此,对于同样大小的图像,当混沌映射的参数及初始值相同时,生成的加密因子是完全相同的,这使得算法极容易被选择明文攻击[5-6]。其次,加密因子直接与图像明文异或,不存在扩散过程,明文敏感性极差,极易受到差分攻击。
1.3 原算法破译
使用选择明文攻击对原算法进行破译。所谓选择明文攻击是指攻击者有机会使用到加密系统,因此可选择一些明文,并产生相应的密文,通过分析明、密文对破译算法。为了破译原算法,选择与待破译密文大小M×N 相等的3个特殊明文矩阵A1、A2及A3。其中,A1为全0矩阵,A2、A3形式如下

由 (2)式可知,A2每一行的元素是相等的,而A3每一列的元素是相等的。使用文献 [10]算法对矩阵Al,l∈[1,3]加密,得到密文矩阵

由于A1为全0矩阵,因此也为全0矩阵,根据式(3)不难破译得到加密因子Ri,j=B1,i,j。A2经列循环移动会保持不变,因此,Acr2与只经过行循环移动的结果是相同的,根据式 (3),

选择3个特殊明文矩阵
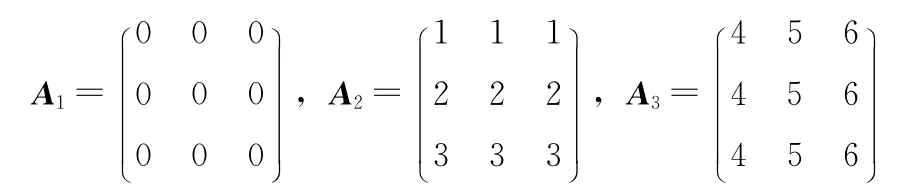
使用文献 [10]算法,获得对应的密文矩阵为
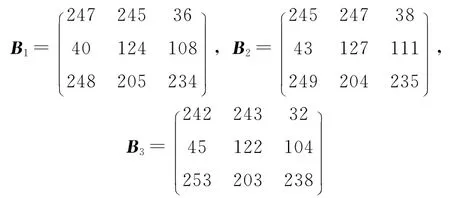
由上述分析可知,加密因子R=B1,而


可见,文献 [10]算法安全性很低。
2 改进的加密算法
针对文献 [10]算法存在的缺陷,提出如下改进措施:首先,改进加密因子的生成方法,使图像中每个质点的坐标与图像明、密文相关联,使生成的加密因子会因图像的不同而不同;其次,改进加密公式,除异或运算外引入算术运算,且使密文与明文、加密因子及相邻密文相关;最后,使用明、密文对混沌映射的参数及初始值进行扰动,使算法做到 “一图一密”。
2.1 替代与扩散
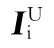
对于上半部分图像序列IUi,按式 (4)对每个像素进行替代与扩散
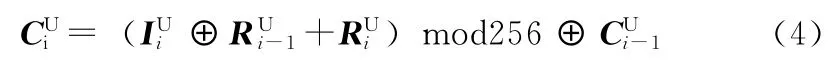
在生成加密因子RUi时,使用tent映射

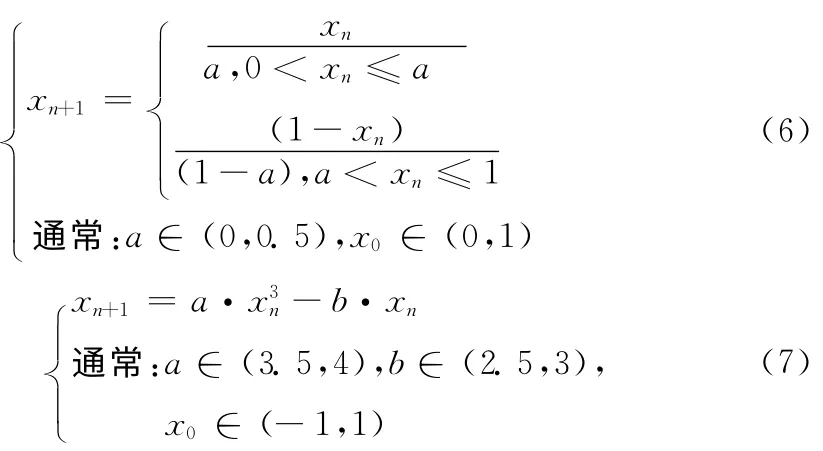
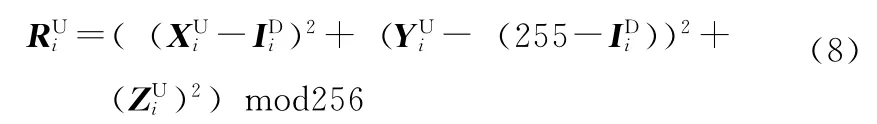
为提高算法安全性,在生成XUi、YUi和ZUi时,使用扰动因子t0、t1,按式 (9)、式 (10)和式 (11)分别对tent映射、kent映射和cubic映射的参数及初始值进行扰动

其中,k1至k7为算法密钥,扰动因子t0由下半部分图像序列的代入,t1由代入。
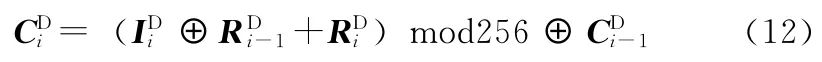

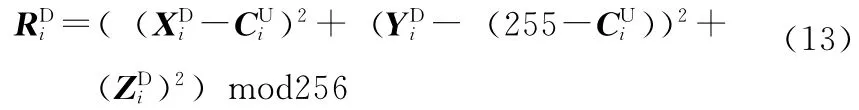
2.2 加密步骤
加密密钥为k0至k8。其中,k0为各混沌映射迭代首部分舍去个数,k1至k7为各混沌映射的参数和初始值,k8为加密轮次,加密步骤如下:
步骤1 输入大小为M×N 的图像I,M 为偶数 (若不满足,可对最后一行复制延拓);
步骤2 使用密钥k0、k1至k7,按2.1节方法对图像进行替代与扩散;
步骤3 判断是否达到k8次的加密次数,若达到,则加密结束,否则将加密结果作为输入图像转至步骤2。
解密是加密的逆过程。密文图像分为上、下子块并转换成密文序列,按

实现每个密文像素的反扩散与反替代。其中,Ci为密文序列,Di为解密后的序列。
3 实验结果与分析
实验中使用1024×1024 的256 色Lena 图,在Matlab7.6环境下仿真测试,密钥k0=100,k1=0.992,k2=0.002,k3=0.422,k4=0.012,k5=3.554,k6=2.564,k7=0.011,k8=2,与文献 [10]和文献 [14]算法进行了比较。其中,文献 [14]使用三维类仿射对图像的像素位置及像素值进行置乱,并按扩散、替代、再扩散的方式对图像加密,每个像素替代时都要进行多混沌映射耦合方式的选择。
3.1 抗统计攻击性能分析
使用改进算法对Lena图进行2轮加密,效果如图1所示,密文图像与原始明文图像的视觉效果完全不同。

图1 Lena图加密效果
图2给出了原始图像和密文图像的直方图。由图2可知,原Lena图的像素值分布非常不均匀,但加密后密文图像的像素值呈平坦且均匀的分布,说明密文像素取各种可能值的概率趋于相等。也可用信息熵来度量图像中灰度值的分布情况[14],对于256级的灰度图,信息熵最大值为8。原Lena图像信息熵为7.219391,以上述初始密钥为起始值,按0.000001步长,连续微调密钥k4及k7100次,加密后密文图像信息熵如图3 所示,均大于7.99980,而计算信息熵均值为7.999843,非常接近最大值8,调整其他密钥可得到类似的结果。以同样的方法,计算文献 [10]密文 图像信息熵均值为7.989682,而文献 [14] 为7.992915,均小于本文改进算法。从直方图及信息熵分析可知,本文改进算法的密文图像灰度分布十分均匀,能有效抵御统计攻击。
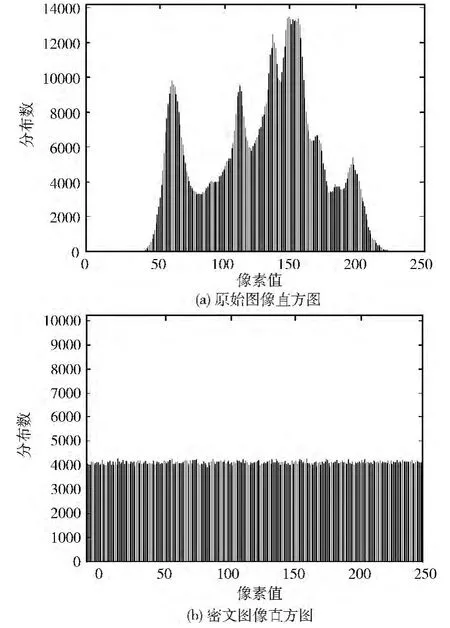
图2 Lena图加密前后直方图
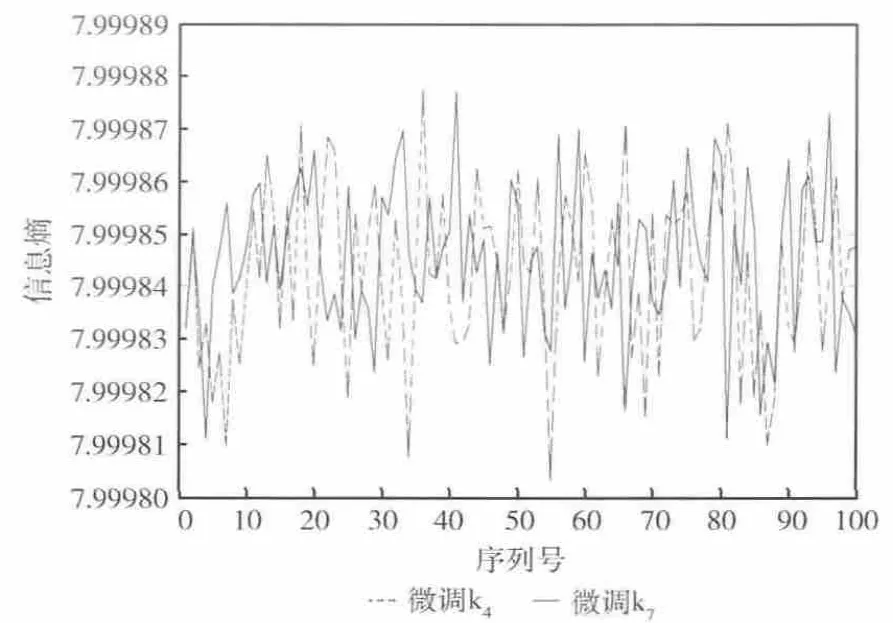
图3 Lena图加密后信息熵
3.2 相关性分析
按文献 [14]方法计算图像中水平、垂直及对角相邻像素的相关系数rxy,若rxy越接近于1,则相邻像素相关性越高,越接近于0,则相关性越低。

图4 相邻像素相关性
原Lena图像水平相邻像素相关系数为0.990671,垂直为0.995407,对角为0.985479。在初始密钥基础上,按0.000001步长,连续微调k1和k3100次,得到密文图像相邻像素相关性如图4所示,密文图像3个方向的相关系数最大值均不超过0.0030,而最小达到3.663405×10-8,微调其他密钥可得到类似结果。以同样的方法,对文献[10]和文献 [14]算法的密钥进行微调,并计算本文改进算法、文献 [10]算法和文献 [14]算法密文图像3 个方向相关系数的均值如表1所示。从表1可知,本文算法密文图像3个方向相关系数的均值都为最小,且非常接近于0,表明本文算法在两轮加密的基础上,虽然没有使用置乱操作,也能很好地破坏相邻像素的相关性,使密文有很好的随机性分布。
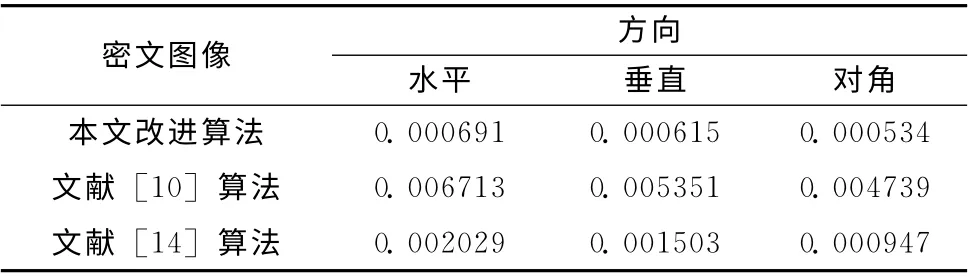
表1 相邻像素相关系数均值
3.3 差分性能分析
好的加密算法应该对明文变化非常敏感,而且这种敏感性越强,抗差分攻击的能力就越强。像素变化率NPCR和像素平均强度变化率UACI是衡量这种敏感性的2个重要指标,其定义可参见文献 [5]。
随机选取原Lena图某一像素,共计100次,使其像素值加1,计算出NPCR和UACI如图5所示,可以看出NPCR均大于0.99595,而UACI均大于0.3340,即明文1个像素的微小变化会导致密文99.595%以上像素的变化,而变化的强度在33.40%以上,这表明算法的明文敏感性很强,有很好的抗差分攻击能力。为便于比较,计算NPCR均值为0.996102,UACI均值为0.334588。以同样的方法求得文献[14]算 法NPCR均值为0.990203,UACI均值为0.331201,均小于本文改进算法。而文献 [10]算法由于不存在扩散过程,因此,明文1个像素的变化只会导致密文1个像素的变化,NPCR和UACI均趋于0,无法抵御差分攻击。

图5 差分性能分析
3.4 密钥空间分析
本文改进算法使用3个混沌映射,共有k1至k77个密钥,若每个密钥使用16位十进制实数表示 (包括1位整数和15位小数),则密钥空间为1016×7=10112,若考虑混沌映射迭代舍去数k0取3位十进制整数,加密轮次k8取1位十进制数,则密钥空间可达10116。可见,本文改进算法具有巨大的密钥空间,能很好地抵御穷举攻击。
3.5 密钥敏感性分析
一个好的加密算法应该对密钥的变化非常敏感。2 个具有微小差异的加密密钥,应该产生完全不同的密文图像;同样,2个具有微小差异的解密密钥,对同一密文的解密结果也应该完全不同。

图6 Lena图解密密钥敏感性测试
解密实验时,分别对密钥k2、k5、k6进行微调 (加上10-15),解密结果如图6所示,可见微小的密钥变化都会导致错误的解密结果。表2列出了微调k2、k5、k6后解密结果之间的NPCR与UACI,结果表明错误的解密结果之间也完全不同,算法具有很强的解密密钥敏感性,微调其他密钥可得到类似结果。
加密实验时,分别微调密钥k3、k7(加上10-15)。表3列出了初始密钥密文、微调k3及微调k7后密文之间的NPCR与UACI,结果表明加密密钥的微小变化会使密文图像截然不同,算法对加密密钥同样非常敏感,其他密钥的微小变化也可得到类似结果。

表2 解密密钥敏感性
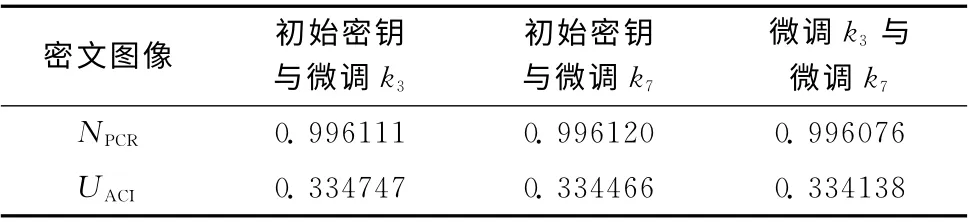
表3 加密密钥敏感性
3.6 执行效率
实验用PC机硬件配置为Intel酷睿i5 双核2.4 GHz处理器,4 G 内存,750 G 硬盘,软件运行环境为windows 7,Matlab7.6。利用本文改进算法对一幅256×256的8位灰度图像进行一轮像素替代与扩散,平均加密时间约为0.021s。文献 [14]算法在相同实验环境下,对同一图像进行一轮加密,平均时间约为0.149s,远高于本文算法。主要原因是文献 [14]在像素替代与扩散之前,使用了三维类仿射变换对图像像素位置和像素值进行置乱,增加了加密时间,同时像素替代与扩散是分开的,并按扩散、替代、再扩散的顺序进行,而且每个像素的替代都要进行混沌耦合方式的选择,增加了算法的复杂度和执行时间。
4 结束语
文献 [10]算法存在设计上的缺陷,容易受到选择明文攻击及差分攻击。因此,提出了改进措施,对图像进行分块加密,使用对方块信息扰动多个混沌映射,并结合对方块信息生成加密因子,使用加密因子和相邻密文对明文进行替代与扩散。分析及实验结果表明改进算法很好地克服了原算法的设计缺陷,具有更高的安全性,且执行效率高。下一步将结合并行加密模型,研究在兼顾安全性的情况下如何进一步提高算法的执行效率。
[1]ZHANG Xiaoqiang,WANG Mengmeng,ZHU Guiliang.Research on the new development of image encryption algorithms[J].Computer Engineering & Science,2012,34 (5):1-6(in Chinese).[张晓强,王蒙蒙,朱贵良.图像加密算法研究新进展 [J].计算机工程与科学,2012,34 (5):1-6.]
[2]ZHANG Yunpeng,ZUO Fei,ZHAI Zhengjun.Survey on image encryption based on chaos [J].Computer Engineering and Design,2011,32 (2):463-466 (in Chinese).[张云鹏,左飞,翟正军.基于混沌的数字图像加密综述 [J].计算机工程与设计,2011,32 (2):463-466.]
[3]Ruouma R,Belghith S.Cryptanalysis of a new image encryption algorithm based on hyper-chaos [J].Physics Letters A,2008,372 (38):5973-5978.
[4]ZHAO Liang,LIAO Xiaofeng,XIANG Tao,et al.Security and efficiency improvement for image encryption algorithm based on high-dimension chaotic system [J].Journal of Computer Applications,2009,29 (7):1775-1778(in Chinese).[赵亮,廖晓峰,向涛,等.对高维混沌系统的图像加密算法安全性和效率的改进 [J].计算机应用,2009,29 (7):1775-1778.]
[5]WANG Jing,JIANG Guoping.Cryptanalysis of a hyper-chaotic image encryption algorithm and its improved version [J].Acta Phys Sin,2011,60 (6):1-11 (in Chinese).[王静,蒋国平.一种超混沌图像加密算法的安全性分析及其改进 [J].物理学报,2011,60 (6):1-11.]
[6]ZHU Congxu,SUN Kehui.Cryptanalysis and improvement of a class of hyperchaos based image encryption algorithms [J].Acta Phys Sin,2012,61 (12):1-12 (in Chinese).[朱从旭,孙克辉.对一类超混沌图像加密算法的密码分析与改进 [J].物理学报,2012,61 (12):1-12.]
[7]TANG Song,XU Guilan,LI Qingdu.New image group encryption algorithm based on high dimensional hyperchaos system and matrix tensor product[J].Journal of Computer Applications,2012,32 (8):2262-2264 (in Chinese). [唐宋,徐桂兰,李清都.基于高维超混沌系统和矩阵张量积的图像分组加密新算法 [J].计算机应用,2012,32 (8):2262-2264.]
[8]PENG Jun,JIN Shangzhu,LIAO Xiaofeng.A novel digital image encryption algorithm based on hyperchaos by controlling lorenz system [C]//Proc of the Fifth International Conference on Natural Computation,2009:395-399.
[9]LI Xiaobo,ZHOU Quan.Remote sensing image encryption algorithm based on composite chaos [J].Computer Engineering and Design,2012,33 (11):4086-4090 (in Chinese).[李晓博,周诠.基于复合混沌的遥感影像加密算法 [J].计算机工程与设计,2012,33 (11):4086-4090.]
[10]GUO Xiaocong,XIANG Fei,LIU Wei.An image encryption algorithm based on multiple chaotic mapping [J].Computer Engineering,2012,38 (20):93-96 (in Chinese).[郭晓丛,向菲,刘伟.一种基于多混沌映射的图像加密算法 [J].计算机工程,2012,38 (20):93-96.]
[11]DUAN Xuefeng,GUAN Jian,DING Yong,et al.Color digital image scrambling algorithm based on multi-group chaotic sequences [J].Computer Engineering,2012,38 (9):114-116 (in Chinese).[段雪峰,关健,丁勇,等.基于多组混沌序列的彩色数字图像置乱算法 [J].计算机工程,2012,38 (9):114-116.]
[12]Benjeddou A,Taha AK,Fournier-Prunaret D,et al.A fast color image encryption scheme based on multidimensional chaotic maps[C]//Proc of Global Information Infrastructure Symposium,2009:1-4.
[13]CHU Ying,WANG Xiaoman,LIU Peng,et al.Research on compound chaos image encryption method with time-varying[J].Journal of Jilin University (Information Science Edition),2012,30 (3):291-296 (in Chinese). [褚影,王小曼,刘鹏,等.基于时钟变换的复合混沌图像加密研究 [J].吉林大学学报 (信息科学版),2012,30 (3):291-296.]
[14]WEN Changci,WANG Qin,HUANG Fumin,et al.Selfadaptive encryption algorithm for image based on affine and composed chaos[J].Journal on Communications,2012,33(11):119-127 (in Chinese).[文昌辞,王沁,黄付敏,等.基于仿射和复合混沌的图像自适应加密算法 [J].通信学报,2012,33 (11):119-127.]
