基于灰度方差和正逆扩散结合的PET重建

上官宏，刘 祎，张 权，桂志国＋

（1.中北大学 电子测试技术国防重点实验室，山西 太原030051；2.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原030051）

0 引 言

正电子发射断层成像（positron emission tomography，PET），融合了核物理学、计算机图形学、医学影像学和分子生物学等前沿学科，能够代表现今核医学技术的先进水平，在脑功能成像和癌症的早期诊断中提供重要的检测信息［1，2］。Bayesian理论指出，MAP算法在ML类算法的基础上添加一项正则化约束即先验分布信息，能够更加准确的描述投影数据的物理模型。但是先验信息选取不当时，则可能影响重建图像的平滑、边缘及噪声特性。所以如何准确地描述先验信息，对PET 重建具有非常重要的意义［3－5］。1982年，Shepp和Vardi首先提出了MLEM 算法，该算法能够考虑系统的物理效应和噪声的统计特性，但速度较慢容易产生棋盘效应。2007年，Yan提出了迭代间各向异性扩散滤波的正则化MLEM（MLEM－PDE），该算法在去除噪声的同时，能很好的保持图像的边缘信息。但是MLEM－PDE所采用的P－M（Perona－Malik）扩散模型仅考虑图像的梯度信息，无法有效保持低梯度值处的细节信息，且对孤立噪声的去除效果不佳［5－9］。本文提出了一种结合图像灰度方差的正逆各项异性扩散模型，该模型采用图像的梯度算子和局部灰度方差共同表征图像的特征，同时考虑前向扩散和后向扩散，对图像的不同区域进行不同的处理。此外，在模糊理论的基础上改进了MLEM－PDE 算法，形成了基于灰度方差和正逆扩散结合的优质PET 重建算法（GVFAB－PML）。实验结果表明，新算法克服了传统模型造成的过度平滑，重建出更加优质的图像。

1 基本理论

1.1 PET统计模型

1982年，Shepp和Vardi首先提出了观测数据的泊松模型，在PET 重建中，采用的离散模型形式为

式中：y＝［y1，y1，…，yN］T表示观测投影数据；f＝［f1，f2，…，fM］T表示图像向量，H 为系统矩阵，ε为非泊松噪声。基于最大似然估计理论，MLEM 算法表示为

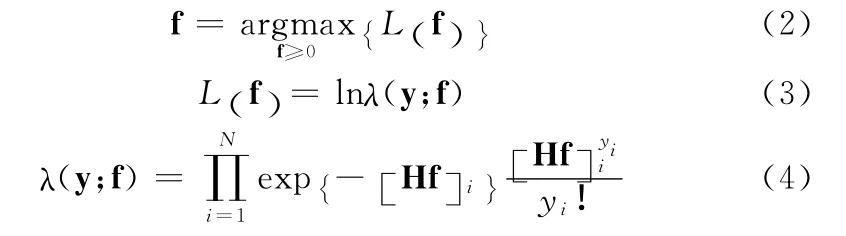
1.2 P－M 扩散模型

各向异性扩散滤波器源于经典的热传导方程，Perona和Malik提出的各向异性扩散模型如下式所示

这里f是梯度算子，g（ f ）为控制扩散强度的扩散系数函数。1990年，Perona和Malik提出

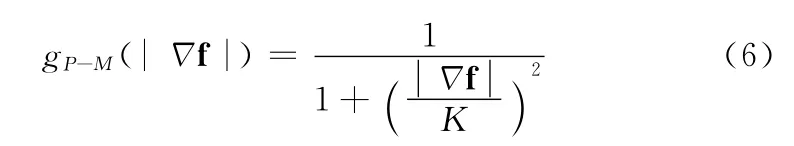
2002年，Gilboa等提出正逆各向异性扩散模型，把图像中梯度较大的地方定义为边缘；梯度较低的部分定义为背景和噪声，对图像的不同区域进行不同的处理。其表达式如下

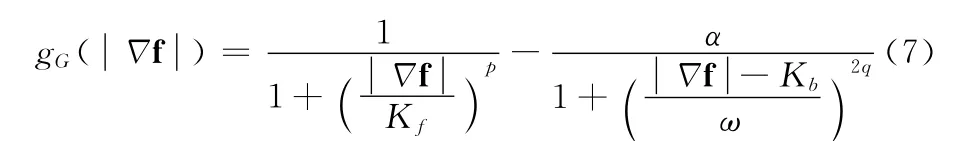
式中：Kf——正向扩散阈值与K 作用相同大致相同，Kb——逆向扩散中心点，与ω共同控制后向扩散的作用范围，α调节正向和逆向扩散的比重。

1.3 非局部MRF二次先验模型

2005年，Buades等最先提出了NL－Means算法，基本思想是：当前像素值由图像中所有与它结构相似的像素加权平均得到。2009 年，Chen等［10］基于非局部均值思想设计了一种非局部MRF二次先验模型，如下式

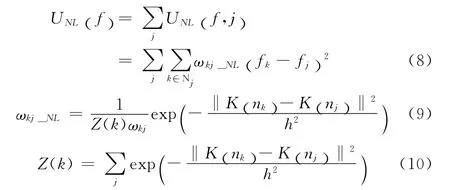
式中：UNL——先验能量，ωkj＿NL——非局部像素k和像素j之间的权值，Z（k）——配分函数。

2 重建算法

2.1 结合图像灰度方差的正逆各项异性扩散模型

针对正逆各项异性扩散模型仅考虑图像梯度信息的不足，本文将2010年Chao［11，12］提出的图像灰度方差引入扩散模型，用图像灰度方差和梯度共同表征图像的特征。认为边缘邻域内的梯度值和灰度方差都比较大，而背景区和含有丰富细节处的梯度值比较小，但后者处灰度方差要明显大于前者。为了防止细节信息丢失，提出的改进扩散模型如下所示

记f 为图像的灰度值，在3×3邻域中计算其灰度方差

式中：珚f——3×3邻域中的平均灰度。因为灰度方差的范围显著大于梯度的范围，将灰度方差按比例缩小，使灰度方差和梯度相互兼容。对于一个8位灰度图像，标准化方差定义为

2.2 基于灰度方差和正逆扩散结合的优质PET重建算法

传统最大似然算法考虑了系统的物理模型和观测数据的统计特性，重建结果较FBP 算法更加优越。但随迭代次数增加，MLEM 棋盘效应严重，重建结果不稳定导致图像退化。针对此问题，本文使用先验惩罚项对MLEM 算法进行约束，提出了基于灰度方差和正逆扩散结合的优质PET重建算法（GVFAB－PML）。每次迭代重建之前，先对当前重建图像进行正逆扩散滤波，然后将Chen 等［12］提出的MRF先验模型引入到最大似然算法中，采用惩罚最大似然算法重建。该算法主要分为两大步骤：

（1）基于改进正逆扩散模型的各向异性扩散

（2）PML重建算法

若将MRF非局部二次先验模型作为惩罚项引入到最大似然算法中，则目标函数变为

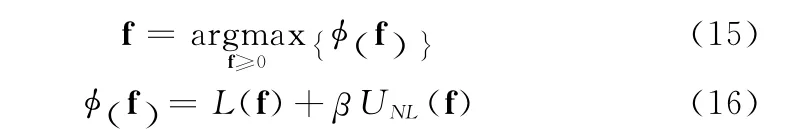
继而，得出其迭代更新方程

3 实验结果及分析

3.1 实 验

本文采用Matlab2008进行算法仿真，利用两组体模数据进行重建：体模1为shepp－logan头部剖面模型；体模2为Thorax胸腔截面模型，体模大小均为128×128，投影数据Sinogram 光子总量近似为1.01×106，投影参数为：128×128，即128个投影方向（均匀分布在0°～180°内）并且每个方向上有128个探测器对。系统矩阵A 经过归一化处理，其规模为（128×128）×（128×128）。在仿真实验中，算法的参数都是根据经验和重建结果手动设定的最优值。本文所有方法迭代次数为100，全局控制参数设为0.9105，邻域窗口大小为3×3。体模数据和观测数据如图1所示。

本文设计了一系列仿真实验，来验证算法有效性，本文算法GVFAB－PML、PML－PDE 与NL－PML，以及传统的MAP、MLEM 等的重建结果如图2、图4所示，各迭代算法重建结果的局部放大图如图3所示。比较图2（a）～图2（g）和图4（a）～图4（g）可以看出，GVFAB－PML、PMLPDE、NL－PML重建效果较传统算法优越性显著，可见各项异性扩散思想的引入极大的改善了重建图像质量。比较图2（d）～图2（f）和图4（d）～图4（f）可知GVFAB－PML、PML－PDE、NL－PML噪声平滑效果都比较好，其中新算法GVFAB－PML去噪效果最好，重建图像与真实图像很接近。在边缘保持方面，比较图3（d）～图3（f）可以看出，NL－PDE算法中间的细小物体部分有大量伪影产生边缘不清晰。PML－PDE算法破坏了物体的边缘结构，特别是中间的细小部分产生了明显的形变。GVFAB－PML算法相对而言能较好的保持边缘，基本保留原有特征。综上，新算法GVFAB－PML在噪声去除和边缘保持方面表现良好，具有优越性。

图1 体模数据和观测数据

图2 体模1各重建算法结果

图3 体模1各重建算法结果局部放大

图4 体模2各重建算法结果

3.2 重建结果量化分析

本文采用均方误差（root mean squared error，RMSE）和信噪比（signal to noise ratio，SNR）来量化分析各重建算法的性能

从图5（a）可知，本文算法GVFAB－PML具有最小的均方误差，这说明它的重建结果与原始图像最接近。且随着迭代次数的增加，曲线趋于平稳。同理从图5（b）可以看出，GVFAB－PML算法信噪比最大，在多次迭代后仍然具有较好的噪声特性，逐渐收敛趋于平稳，算法优越性得到直观体现。为了更加清楚的描述各质量参数，表1给出了本文所用重建算法的量化数据。

分析表1可知，由于各项异性扩散思想的引入，GVFAB－PML、PML－PDE算法较NL－PDE，以及传统的MAP、MLEM 算法在噪声平滑方面有大幅度的改善。与其它几种算法相比，NL－PML 算法的去噪表现非常优异，量化的反映了非局部均值滤波和各向异性扩散算法在降噪方面的优越性。同理分析均方误差，MAP算法均方误差值很大，说明边缘细节信息丢失，伪影严重。GVFAB－PML、PML－PDE算法较NL－PML，以及传统的MAP、MLEM 的重建质量得到改善，细节更加清晰。从表中数据可以看出，本文算法GVFAB－PML 在细节保持方面的改善最为明显。综上分析，GVFAB－PML算法在图像质量改善和噪声平滑方面都有改进，算法可行性得到验证。

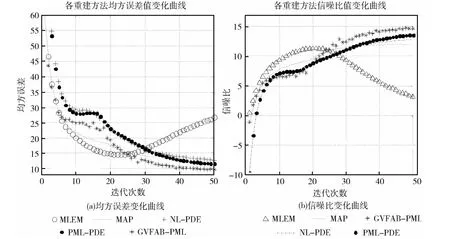
图5 各重建算法评估参数变化曲线

表1 图1中所示重建图像的评估对比

4 结束语

本文提出了一种结合图像灰度方差的正逆各项异性扩散模型，该模型采用图像的梯度算子和局部灰度方差共同表征图像的特征，同时考虑正向扩散和逆向扩散，对图像的不同区域进行不同的处理。文中GVFAB－PML 算法，结合了模糊理论和各向异性扩散的优点，克服了传统模型造成的过度平滑，保留了细节信息。

设计了一系列仿真实验，来验证所提算法的优越性。给出了整体和局部对比图，对比分析了各算法的噪声平滑效果及细节特性。实验结果表明，无论从视觉效果还是客观准则来看，GVFAB－PML 算法在图像质量改善和噪声平滑方面都有改进，算法可行有效。

［1］Rahmim A，Zaidi H.PET versus SPECT：Strengths，limitations and challenges ［J］.Nuclear Medicine Communications，2008，29 （3）：193－207.

［2］Rahmim A，Dinelle K，Cheng J C，et al.Accurate event－driven motion compensation in high－resolution pet incorporating scattered and random events［J］.IEEE Transactions on Medical Imaging，2008，27 （8）：1018－1033.

［3］ZHOU Jian.Image reconstruction for positron emission tomography ［D］.Nanjing：Southeast University，2006 （in Chi－nese）.［周健.正电子发射断层的图像重建方法研究 ［D］.南京：东南大学，2006.］

［4］HUANG Jing，MA Jianhua，LU Lijun，et al.Generalized Gibbs priors in positron emission tomography ［J］.Dianzi Xuebao（Acta Electronica Sinica），2010，38 （4）：899－903 （in Chinese）.［黄静，马建华，路利军，等.基于广义Gibbs先验的优质PET 成像 ［J］.电子学报，2010，38 （4）：899－903.］

［5］YAN Jianhua.Investigation of positron emission tomography image reconstruction ［D］.Wuhan：Huazhong University of Science ＆Technology，2007 （in Chinese）.［颜建华.正电子发射断层图像重建算法研究 ［D］.武汉：华中科技大学，2007.］

［6］HE Jiawei.The research of positron emission tomography statistical iterative algorithm and acceleration methods ［D］.Taiyuan：North University of China，2011 （in Chinese）.［何佳伟.正电子发射断层成像的统计迭代方法及加速方法研究［D］.太原：中北大学，2011.］

［7］Gui Z，Liu Y，He J.PML algorithm for positron emission tomography combined with nonsocial fuzzy anisotropic diffusion filtering ［J］.IEEE Transactions on Nuclear Science，2012，59 （5）：1984－1989.

［8］Gui Z，He J.Regularized maximum likelihood algorithm for PET image reconstruction using a detail and edges preserving anisotropic diffusion ［J］.Optik－International Journal for Light and Electron Optics，2012，123 （6）：507－510.

［9］Zhang Q，Liu Y，Shu H，et al.Application of regularized maximum likelihood algorithm in PET image reconstruction combined with nonlocal fuzzy anisotropic diffusion ［J］.Optik－International Journal for Light and Electron Optics，2013，124（20）：4561－4565.

［10］CHEN Yang.High quality PET image reconstruction based on different prior acquisitions［D］.Guangzhou：Southern Medical University，2007 （in Chinese）.［陈阳.基于不同先验获取的PET 图像优质重建新方法研究 ［D］.广州：南方医科大学大学，2007.］

［11］Chao S M，Tsai D M.An improved anisotropic diffusion model for detail－and edge－preserving smoothing ［J］.Pattern Recognition Letters，2010，31 （13）：2012－2023.

［12］Chao S M，Tsai D M.Anisotropic diffusion with generalized diffusion coefficient function for defect detection in low－contrast surface images ［J］.Pattern Recognition，2010，43 （5）：1917－1931.