改进的基于特征点匹配的图像拼接融合算法
2014-12-23焦丽龙李定主
焦丽龙,韩 燮,李定主
(1.中北大学 计算机与控制工程学院,山西 太原030051;2.北方自动化控制研究所,山西 太原030051)
0 引 言
图像拼接技术正广泛应用于计算机图形图像处理、医学图像和虚拟现实等领域,关键技术是配准和融合,配准是根据图像之间重叠区的一致性求出图像之间的投影变换,融合[1]是实现无缝拼接。
目前,国内外已经提出了很多种图像拼接方法,一般分为基于区域[2]和基于特征[3,4]的方法。其中,基于区域的方法往往由于亮度、对比度的不同导致拼接失败,而基于特征方法的匹配效果相对稳定,并且运算效率高。其中,SIFT[5]算法是目前研究最多、应用最广泛的一种。但是该算法仅利用了局部邻域信息,所以当待匹配图像有大量的相似结构时,相似结构中的点极易发生误匹配。目前剔除误匹配点对的主要方法是采用极几何约束和迭代求精。然而用传统的RANSAC[6]算法效率很低,特别是当匹配特征点对的 “内点”(准确匹配点)比例比较小时,会直接影响到拼接算法的效率。文献[7]提出的基于中值滤波的特征点对匹配算法,不能完全剔除误匹配点,且执行效率较低。文献[8]提出用中值滤波检测RANSAC 的初始迭代特征点对,该方法没有考虑剔除误匹配点,对RANSAC的执行效率没有实质的改进。本文针对误匹配造成内点比例低时,RANSAC算法效率低、配准不稳定的问题,提出了一种新的方法预筛粗匹配点对,再使用RANSAC算法提纯,来提高算法效率和配准稳定性。图像融合部分,采用加权平均算法来解决因曝光参数不同而存在的亮度差异。
1 SIFT特征点提取
1.1 SIFT算法介绍
SIFT 算法于1999年首次被Lowe提出(SIFT 算法定义请参见文献[9]),该算法提取的特征具有平移、缩放、旋转的不变性,并且对光照、仿射及投影的变化也有一定的鲁棒性。
1.2 特征点提取
SIFT 算法是在不同的尺度空间上进行特征检测,而高斯核具有线性、平移、旋转不变性等特点,所以只有高斯核才可以构成多尺度空间的核[10]。提取特征点的步骤:
(1)确定特征点。将一个图像的尺度空间表示为L(x,y,),它是由一个可变尺度的高斯函数G(x,y,)和原始图像I(x,y)的卷积产生的,即

其中
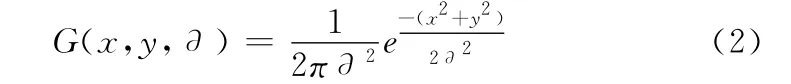
在图像的二维平面空间和DoG(difference-of-Gaussian)尺度空间中同时检测局部极值作为特征点,使得特征点具有良好的独特性和稳定性。将待检测的点与其所在层的点比较,如果是极值,则该点作为SIFT 的候选点。DoG 的响应值图像D(x,y,)是两个相邻高斯尺度空间的图像相减得到的,其具有计算简单的特点,是LoG(Laplacian-of-Gaussian)的近似。其中

式中:k——两相邻尺度空间倍数的常数。
检测D(x,y,)的局部极值。每个采样点都要与其同尺度的8个相邻点和尺度中相邻图像的18 个相邻点进行比较,把找到的极值点作为侯选特征点提取出来。通过尺度空间DoG 函数的曲线拟合和Hessian 矩阵方法去除不稳定的点。
(2)为特征点分配主方向。用L(x,y)表示图像,则图像中点(x,y)处的幅角m(x,y)和幅值θ(x,y)的计算公式如下
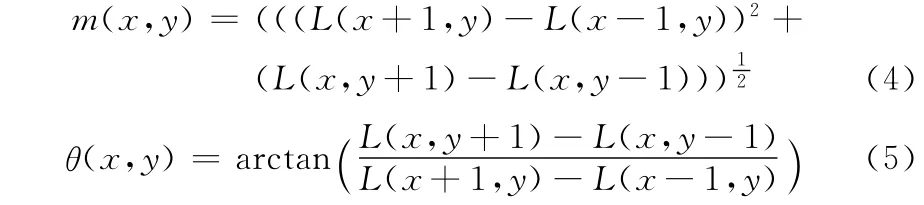
对图像中的每个特征点分别用式(4)和式(5)计算,然后使用直方图统计该特征点的幅角和幅值,峰值就是该特征点的主方向。
2 特征点匹配与筛选
图像的SIFT 特征点提取后,从待匹配图像中选择一个特征点,采用优先k-d树[11]从基准图像中查找与该点欧氏距离最近的前两个特征点,从而得到距离最近的与距离次近的比值,若比值小于给定的阈值,则认为距离最近的点为匹配点。欧氏距离计算公式
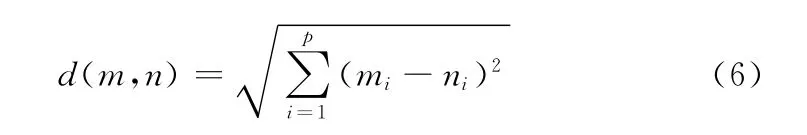

2.1 传统的RANSAC算法
采用欧氏距离比值匹配的粗匹配点对包含大量误匹配。为了增强算法的鲁棒性,使用经典的RANSAC 算法剔除误匹配。该算法的原理是:随机选择n个样本估计模型参数,再利用得到的模型计算,把小于阈值的匹配点作为内点。重复C 次以上过程,选择包含内点最多的点集计算出准确的模型参数。
其中估计次数C 是影响算法效率的主要参数,计算公式
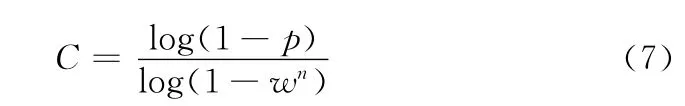
式(7)表示,经过C 次至少有一次估计中的所有数据点都是内点的概率是p。其中,w 为内点概率,n 为确定模型参数的最少点数。
RANSAC算法能够剔除误匹配点对,并且实现简单,因此在图像处理中到了广泛应用。但是该算法在内点概率w 很小时,估计次数高达567 次,导致其运算效率低下。该算法的估计次数C 与集合中内点比例关系见表1。

表1 估计次数C 与集合中内点比例关系
因此本文提出添加约束的方法预筛选粗匹配点对,提高内点的比例,大大减少估计次数,来提高RANSAC 算法的运算效率。
2.2 改进的RANSAC算法
针对传统的RANSAC 算法,内点的概率w 很小时,估计次数高,导致算法运算效率低的问题,在运用RANSAC算法提纯前,采用分类分析统计技术,根据相邻匹配点对的特征点距离大致相等的特性对其进行筛选。图像A 和图像B 表示待匹配的图像,根据式(8)计算特征点对距离差,设置阀值υ进行筛选

式中:aij、bij——图像A、图像B 的第i个和第j 个特征点之间的距离。特征点分别取自图像A 和图像B 的粗匹配点集合m=(m1,m2,…,mp)和n=(n1,n2,…,np)。
算法具体可分以下4个步骤:
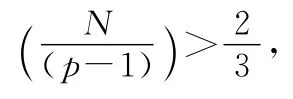
(2)剔除误匹配点对。求出其余所有点对与4 对正确点对的距离,然后与阀值υ进行比较,并统计出小于阀值υ的次数,将次数小于3次的匹配点对剔除。
(3)使用RANSAC 算法对筛选出的特征点对进行提纯,求解变换矩阵。
(4)根据变换矩阵,完成统一坐标变换。
2.3 误匹配点剔除算法步骤
Algorithm:SelectCorrectPair
Input:T={(Mij,Nij),i,j=1,2,…,p,j≠i}
Output:P={pi,i=1,2,…,t,t≤p}
1.Initialization:O={oi,i=1,2,3,4}count=0num=0
2.if|Mij-Nij|<υand count<4then
3.num=num+1
5.count=count+1
6.oi=i
7.end while
8.num=0
9.end if
10.if|Mjoi-Njoi|<υthen
11.count=count+1
12.while count>2
13.pi=j
14.end while
15.count=0
16.end if
17.return P
算法的输入是两个图像的特征点对的距离差集合,输出为正确匹配点对在粗匹配点对中的序号。先将距离与阀值的比较找到4对正确点对,然后求出其它点对与这4对正确点对的距离集合,再将距离集合与阀值比较,如果同一点对与大于2对正确点对的距离小于阀值,则该点对被确定为正确匹配点对。
2.4 求解变换矩阵
将两幅图像之间的变换矩阵表示为H,设m(i,j),n(i′,j′)是正确匹配的点对。经过齐次坐标变换,得到H的求解公式

根据式(9),理论上只需4组数据便可计算出变换矩阵的8个参数。然后将待拼接图像根据所求的变换矩阵转换,完成统一坐标变换。
2.5 融合部分
图像拼接后往往因为两张图像的曝光参数不同而产生明显的拼接线,本文采用加权平均算法来处理拼接线。设A(i,j),B(i,j)是待拼接的两张图,重叠区域图像的像素C(i,j)的计算公式为

其中 =(i2-i)/(i2-i1),i1<i<i2。i1,i2分别是重叠区域x轴的最小和最大值。
3 实验结果及分析
实验平台为Windows XP系统,1.8GHz主频,2GB内存,利用Matlab R2012b编程进行实验。实验数据来源于在校园内拍摄的22组800×1066分辨率的照片。实验的算法流程如图1所示。
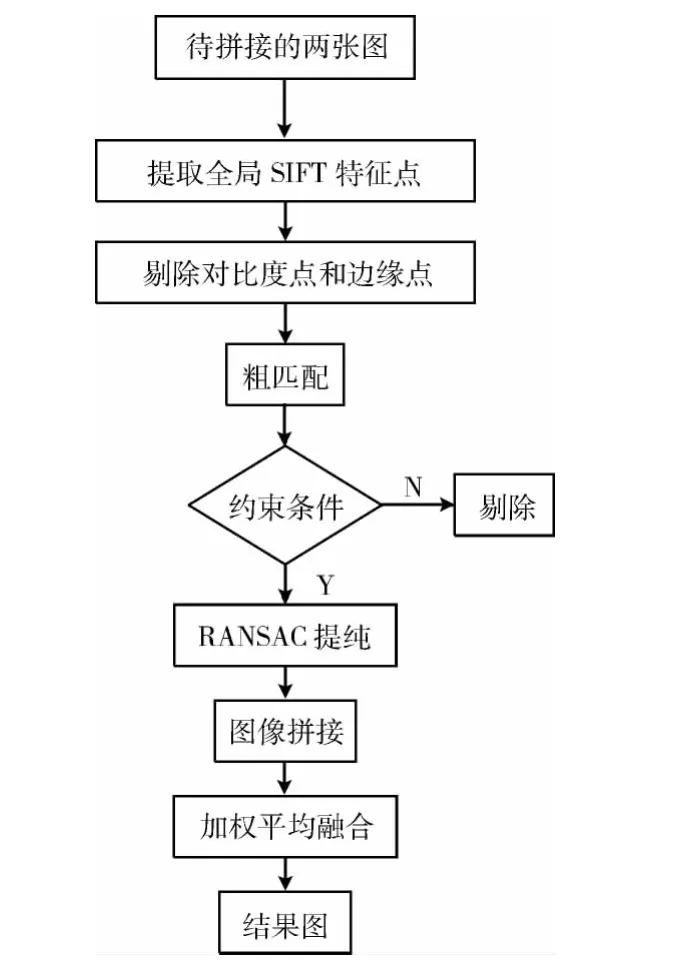
图1 实验算法整体流程
图2(a)(大小已放缩)是22 组照片中的1 组照片的原图,图2(b)是SIFT 算法提取图片的特征,图2(c)是特征点对筛选前后匹配对比,图2(d)是最后的效果图。
统计结果见表2,从表2中可以看出,预筛选后迭代特征点对减少了68.9%,耗时减少了59.9%。筛选前后匹配点对对数对比如图3(a)所示,原算法与改进算法耗时对比如图3(b)所示。

图2 原图、提出特征点图和匹配特征点对比图及最后效果

表2 统计结果
表2中平均运行时间=运行总时间/总组数,平均迭代特征点对=迭代总对数/总组数。
实验结果表明:采用分类统计技术添加约束条件,对粗匹配点对进行外点剔除,有效提高了内点的概率,从而减少了RANSAC 算法的估计次数,提高了算法的运行效率,拼接效果较好;加权平均算法处理拼接线,较好地解决了因曝光参数不同而存在的亮度差异。
4 结束语

图3 优化前后特征点对数和算法耗时对比
本文通过SIFT 算法提取图像的特征点,在特征点匹配阶段添加约束条件剔除误匹配点对,提高了内点的概率,有效减少了RANSAC算法的估计次数,得到稳定的变换矩阵,用加权平均算法实现拼接图像融合。提高了算法的效率和配准精度。实验结果证明,该算法对视差和光照变化较大的图像拼接效果较好,但是对于实时拼接的应用,该算法还有待进一步完善。
[1]ZHANG Ruijuan.Study on the theory and algorithm of image registration [D].Xi’an:Xidian University,2009 (in Chinese).[张锐娟.图像配准及算法研究 [D].西安:西安电子科技大学,2009.]
[2]Bay H,Ess A,Tuytelaars T,et al.Speeded-up robust features(SURF) [J].Computer Vision and Image Understanding,2008,110 (3):346-359.
[3]Zheng Zhibin,Ye Zhongfu.Image registration algorithm based on phase-correlation [J].Journal of Data Acquisition and Processing,2006,21 (4):444-449.
[4]Guizar-Sicairos M,Thurman ST,Fienup J R.Efficient subpixel image registration algorithms[J].Optics Letters,2008,33 (2):156-158.
[5]Brown M,Lowe D G.Automatic panoramic image stitching using invariant features[J].International Journal of Computer Vision,2007,4 (1):59-73.
[6]LIU Kun,GE Junfeng,LUO Yupin,et al.Probability guided random sample consensus[J].Journal of Computer-Aided Design and Computer Graphics,2009,21 (5):657-662 (in Chinese).[刘坤,葛俊锋,罗予频,等.概率引导的随机采样一致性算法 [J].计算机辅助设计与图形学学报,2009,21(5):657-662.]
[7]ZOU Beiji,RUAN Peng,XIANG Yao.An exact match automatic panorama stitching algorithm [J].Computer Engineering and Science,2010,32 (8):60-63 (in Chinese). [邹北骥,阮鹏,向遥.一种精确匹配的全景图自动拼接算法 [J].计算机工程与科学,2010,32 (8):60-63.]
[8]FANG Xianyong,ZHANG Mingmin,PAN Zhigeng,et al.A new method of manifold mosaic for large displacement images[J].Journal of Computer Science and Technology,2006,21(2):218-223.
[9]WANG Yongming,WANG Guijin.Image local invariant features and description [M].Beijing:National Defense Industry Press,2010 (in Chinese).[王永明,王贵锦,图像局部不变性特征与描述 [M].北京:国防工业出版社,2010.]
[10]ZHU Licheng,YAO Minghai.Object matching algorithm based on SIFT and identification [J].Mechanical and Electrical Engineering,2009,26 (4):73-75 (in Chinese).[朱利成,姚明海.基于SIFT 算法的目标匹配和识别 [J].机电工程,2009,26 (4):73-75.]
[11]LIN Lujun,SUN Lingling,LI Xungen,et al.An improved template matching based microscopic cell image mosaic algorithm [J].computer software and application,2010,27(1):108-110 (in Chinese). [林陆军,孙 玲 玲,李 训 根,等.一种改进的基于模板匹配的显微细胞图像拼接算法 [J].计算机应用与软件,2010,27 (1):108-110.]
