连铸圆坯结晶器锥度优化设计研究
2014-12-22刘建敏董亮朱新华刘增勋朱立光
刘建敏 董亮 朱新华 刘增勋 朱立光
(1.中钢集团石家庄设计院, 2.唐山国丰钢铁有限公司; 3.河北联合大学)
0 引言
在连铸生产过程中,为了保证坯壳与结晶器壁的良好接触,在设计结晶器时应尽可能确定合适的锥度。锥度过大,坯壳与结晶器的摩擦增加,引起结晶器液面波动,加剧结晶器的磨损,甚至造成粘结漏钢。锥度过小,坯壳与结晶器壁间气隙增大,热流减小坯壳变薄;坯壳生长不均匀性增加,导致纵裂纹甚至发生漏钢。在结晶器锥度优化研究中,数值模拟得到广泛应用[1-3]。通过建立热力耦合模型,分析无锥度结晶器内气隙分布状态,基于最小气隙原理,对结晶器锥度进行一次性优化。
优化锥度改善了结晶器与坯壳的接触状态,结晶器热流升高。同时,由于结晶器内坯壳温度降低,表面收缩也相应增加,坯壳与结晶器之间将会重新形成气隙,削弱了结晶器锥度的优化效果。本次研究建立圆坯结晶器内坯壳热力耦合模型,利用有限元软件ANSYS 对结晶器内坯壳变形进行分析。根据结晶器内坯壳气隙分布状态,基于最小气隙原理,通过多次优化确定结晶器内腔形状。
1 数学模型
1.1 模型建立
基于圆坯轴对称性以及前人研究经验[3-6]对结晶器传热进行适当简化:①忽略圆周方向传热和变形,建立二维轴对称热力耦合模型;②物理模型采用结晶器内铸坯沿轴向1/2 纵切片;③钢的物性参数仅与温度有关,忽略各向异性;④假设坯壳与结晶器间的气隙完全被保护渣填充;⑤采用弹塑性模型,服从Von Mises 屈服准则,遵循Prandtl-Reuss 增量理论。
通过以上简化,铸坯在结晶器传热简化为二维非稳态导热过程,采用柱坐标系导热方程进行描述:
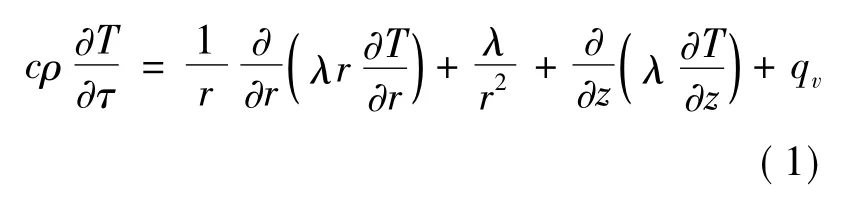
式中:c——热容,J/( kg·℃) ;
ρ——密度,kg/m3; Τ——温度,℃;
τ——时间,s; qv——内热源,W/m3;
λ——导热系数,W/( m·℃) ;
r、z——径向坐标和高度坐标,m。
弹塑性模型增量关系的应力应变数学表达式:
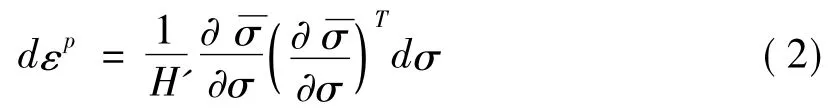
式中:εp——塑性应变;
H'——应力- 塑性应变曲线的斜率;
采用细化表面网格、MAP 划分方式和拉坯方向均匀网格,使有限元网格符合坯壳的传热和变形规律。建立的圆坯的有限元模型如图1 所示。

图1 有限元网格划分示意图
1.2 初始条件和边界条件
采用浇注温度作为初始温度,在模型上下边界施加绝热边界条件。铸坯表面传热采用综合传热系数,坯壳表面与结晶器内壁间的总热阻为结晶器内壁与保护渣界面热阻、气隙热阻、保护渣热阻以及铸坯与保护渣界面热阻之和; 冷却水与铜壁间为对流传热。结晶器内钢液与冷却水之间传热过程的总热阻可以表示为:
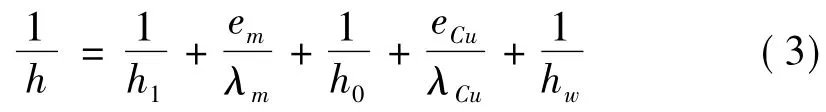
式中:h——钢液与冷却水间综合传热系数,W/(m2·℃);
h1——钢液与坯壳间的传热系数,W/(m2·℃);
em——坯壳厚度,m;
λm——钢导热系数,W/( m·℃) ;
h0——坯壳与结晶器铜壁间的等效传热系数,W/( m2·℃) ;
eCu——结晶器铜壁厚度,m;
λCu——铜导热系数,W/( m·℃) ;
hw——结晶器铜壁与冷却水间的传热系数,W/( m2·℃) 。
在凝固前沿固相率为0.7 的界面上施加钢水静压力。把结晶器壁处理成刚体,通过控制刚体的移动来约束铸坯表面位移。当坯壳表面未穿透结晶器铜壁,表面采用自由边界;若表面膨胀较大穿透结晶器壁,则按结晶器锥度对表面进行位移约束[4]。
1.3 分析方法
采用有限元软件ANSYS,对二维非稳态温度场以及坯壳应力进行数值模拟分析。利用ANSYS 提供的多载步法,实现应力遗传分析[5]。根据应力分析得到的气隙分布,对铸坯表面的综合传热系数进行不断修正。为简化模型运算,假设铸坯模型静止,通过结晶器向上移动来模拟拉坯过程。具体计算过程如图2 所示。
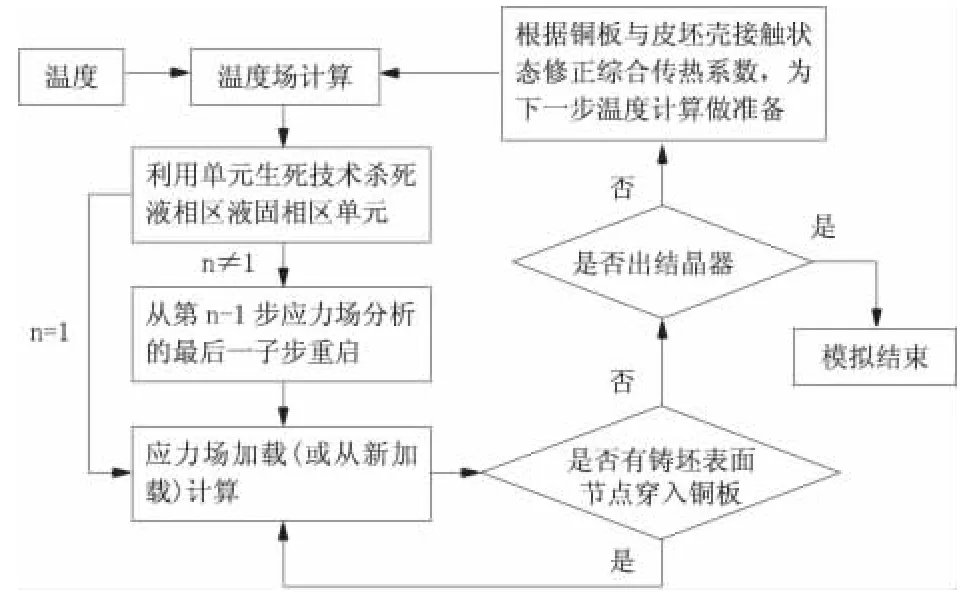
图2 模型分析过程
首先,分析无锥度时结晶器内坯壳与铜壁间的气隙分布,根据最小气隙原则设计结晶器锥度; 其次,以设计锥度为坯壳变形边界条件重新进行模拟计算,利用得到的气隙分布状态对锥度进行优化;然后,以优化结果为边界条件,重新分析坯壳与结晶器壁间气隙与压力分布。如此不断优化,当气隙或压力达到一定要求时,完成锥度优化设计。
2 优化过程
采用某厂圆坯连铸的工艺参数进行分析: 钢种Q195,圆坯直径Φ310 mm;结晶器铜壁厚度18 mm,总长度900 mm,有效长度820 mm;浇注温度1555 ℃,拉速0.8 m/min; 结晶器冷却水温度30 ℃,冷却水速度8.4 m/s。
2.1 锥度初步设计
首先模拟在无锥度结晶器内铸坯凝固过程,分析坯壳自由收缩性。采用无锥度结晶器浇注Q195 钢时,坯壳表面径向收缩量沿拉坯方向分布,如图3 所示。
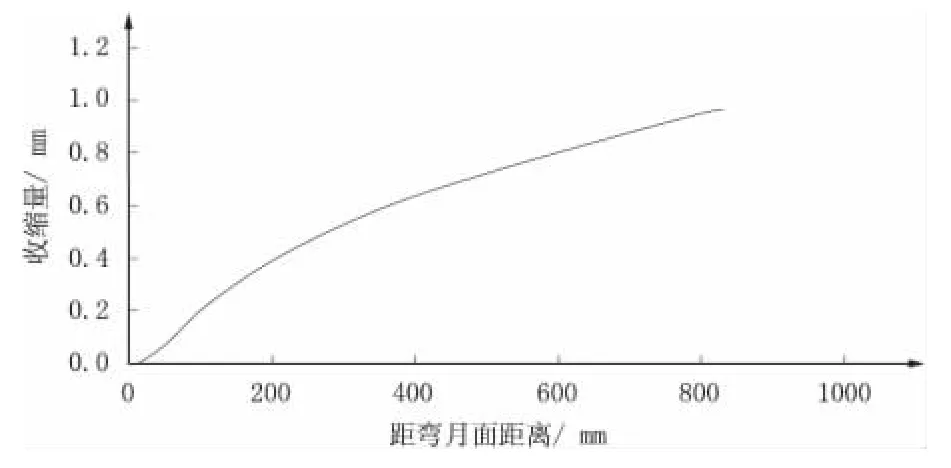
图3 无锥度结晶器内气隙分布
由图3 可以看出,随着离开弯月面距离的增加,坯壳表面收缩量逐渐变大。在结晶器出口处,铸坯收缩达到最大值0.96 mm。根据气隙分布,对结晶器锥度进行设计,得到的结晶器内腔尺寸,如图4 所示。
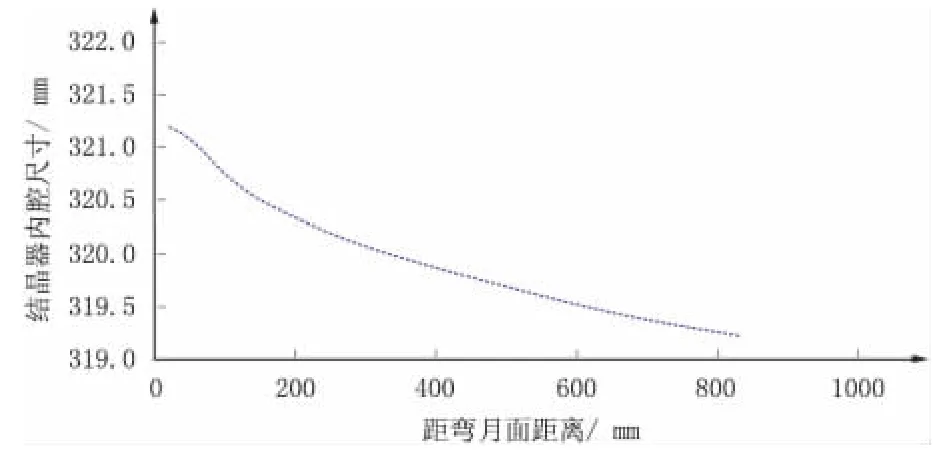
图4 结晶器内腔初步设计曲线
由图4 可以看出,结晶器内腔呈抛物线状。在结晶器上部坯壳收缩较快,在结晶器中下部收缩逐渐减缓。初步设计的结晶器总锥度为0.73 % /m。
2.2 第一次锥度优化
以初步设计锥度为坯壳变形的边界条件,在相同的工艺条件下重新模拟热力耦合分析,得到的沿拉坯方向气隙分布,如图5 所示。
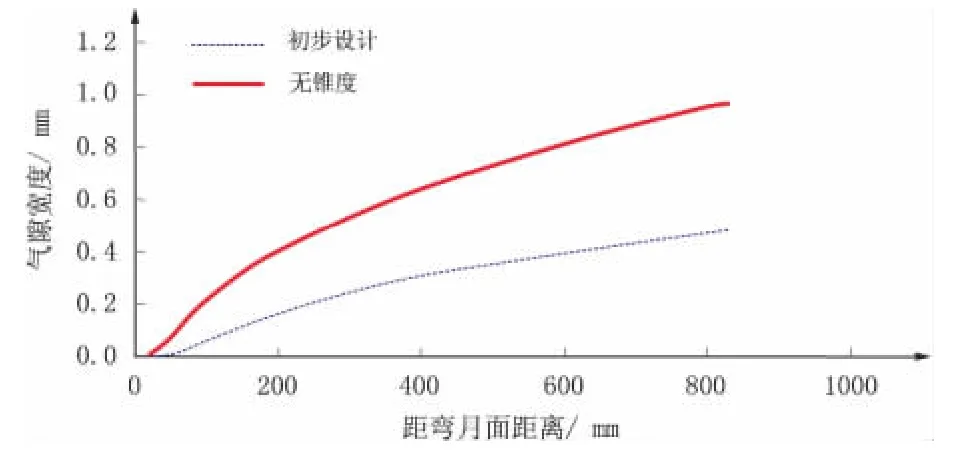
图5 设计结晶器内气隙分布
由图5 可以看出,采用设计锥度后,虽然消除了无锥度时的气隙,但是由于结晶器传热状态改善,坯壳温度下降收缩增加,气隙又重新形成。与无锥度结晶器相比,气隙宽度大幅度降低,最大气隙宽度由0.96 mm 降低到0.47 mm。同时,从弯月面附近至结晶器出口,坯壳与结晶器壁间存在贯通气隙,坯壳与结晶器壁间压力为零。由于气隙较宽,不能满足传热要求,需要对结晶器锥度进行优化。
根据最小气隙原则,在结晶器初步设计锥度基础上,结合结晶器内气隙分布状态,对结晶器锥度进行第一次优化,优化结果如图6 所示。
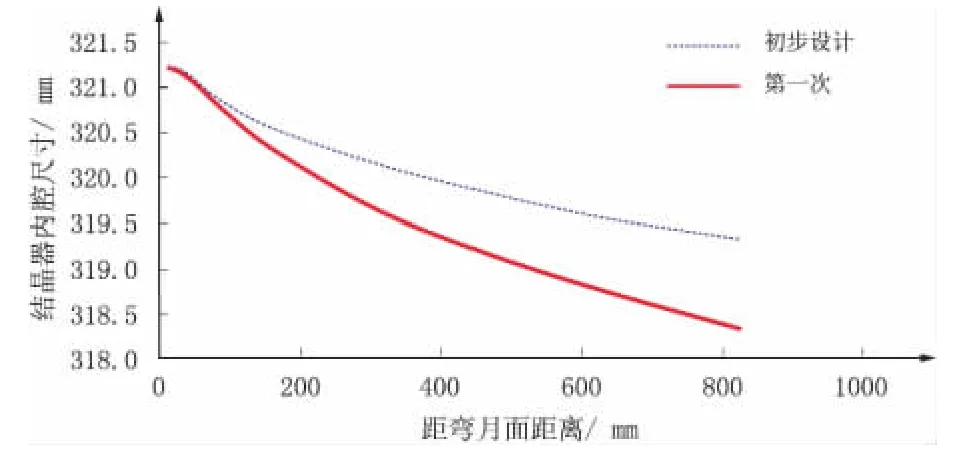
图6 第一次结晶器内腔优化曲线
由图6 可以看出,第一次优化后的结晶器内腔也呈抛物线状,总锥度提高到1.08 % /m。
2.3 第二次锥度优化
同样,在相同的工艺条件下,采用第一次优化锥度重新对坯壳变形情况进行模拟计算,分析气隙和压力分布状态。气隙分布状态如图7 所示。
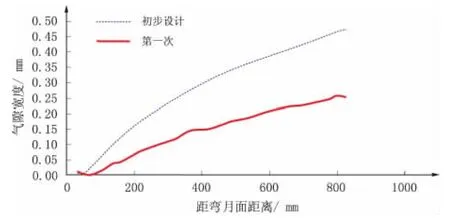
图7 第一次优化结晶器内气隙分布
由图7 可以看出,采用第一次优化锥度后,结晶器内气隙宽度整体下降,气隙最大宽度由0.47 mm下降到0.25 mm。但是,在整个结晶器内仍然存在较宽的气隙,对结晶器传热仍存在一定制约,应对结晶器锥度进行第二次优化。
根据气隙分布情况对第一次优化锥度结果进行再次优化,结晶器总锥度达到1.88 % /m,结晶器内腔尺寸如图8 所示。
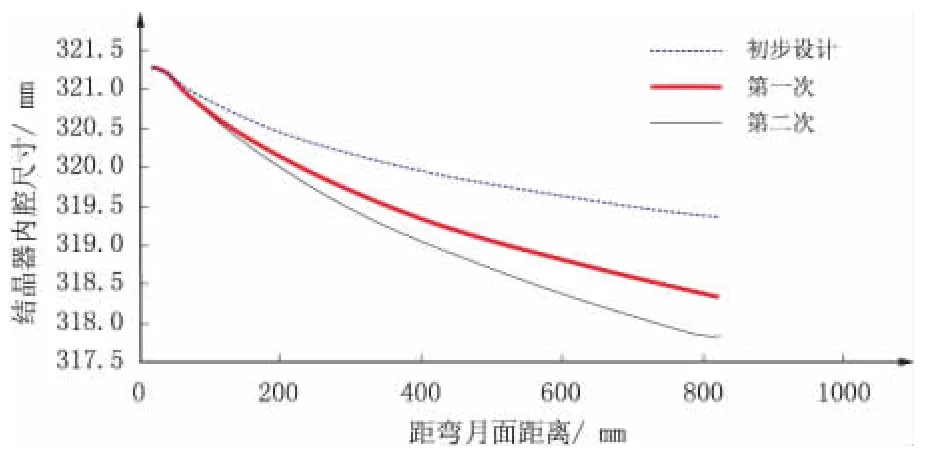
图8 第二次结晶器内腔优化曲线
3 结果与分析
采用第二次结晶器锥度优化结果重新进行铸坯热力模拟分析,得到的结晶器与坯壳间气隙沿拉坯方向的分布,如图9 所示。
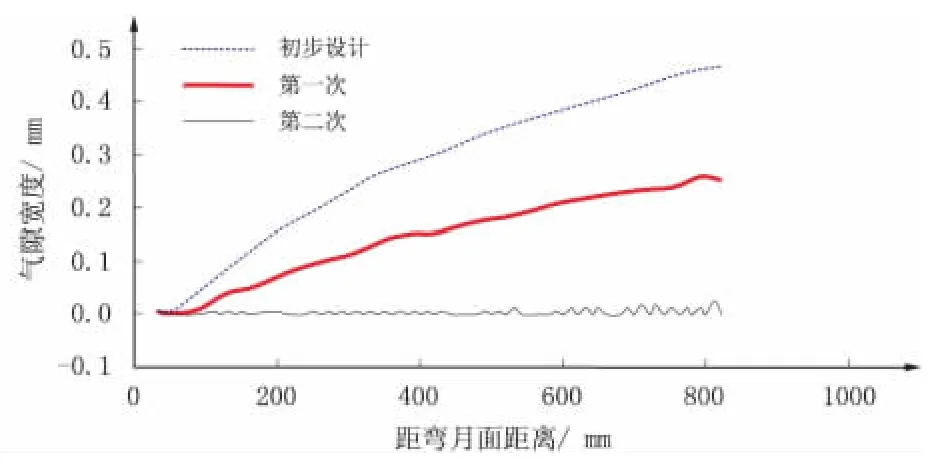
图9 第二次优化结晶器内气隙分布
由图9 可以看出,采用第二次结晶器锥度优化结果进行铸坯热力模拟分析时,气隙出现较大波动,随着铸坯的下行气隙不断消失、生成。这是由于在弯月面附近,冷却速度快,钢液很快凝固形成初生坯壳,随着温度降低,坯壳内部产生收缩应力,使得坯壳脱离结晶器内壁。
而坯壳与铜壁的分离导致两者界面上产生气隙,气隙热阻极大,坯壳生长减慢,同时液相过热和凝固潜热的继续导出会使坯壳温度回升,导致坯壳强度变差。随着铸坯向下移动,逐步增大的钢水静压力将已脱离铜板的坯壳又压回结晶器铜壁,气隙消失,坯壳与铜壁重新接触。上述过程不断反复,直到坯壳出结晶器为止。
与采用第一次优化后结晶器锥度模拟计算结果不同,此次气隙最大宽度值为0.021 mm,能够满足浇注要求。但是在结晶器内未出现气隙处,坯壳可能对结晶器壁产生较大摩损,所以还需要考虑坯壳与结晶器壁间摩擦力的变化。
根据物理学原理,摩擦力与压力成正比。因此,可以利用坯壳与结晶器壁间的压力来描述坯壳与结晶器壁间摩擦力的变化。结晶器内坯壳与结晶器壁间压力沿拉坯方向的变化如图10 所示。
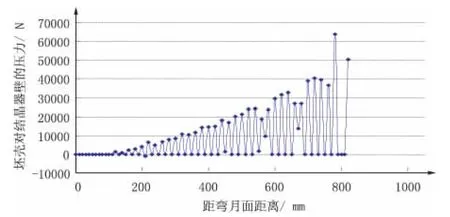
图10 坯壳与结晶器壁间的压力变化
由图10 可以看出,沿拉坯方向,坯壳与结晶器壁间压力时有时无,但压力值呈增大趋势,这与分析得到的气隙分布规律基本一致。
4 结论
基于圆坯轴对称性,建立了二维纵向切片圆坯热力耦合模型,利用有限元分析软件ANSYS 实现了结晶器内圆坯传热和变形分析。经过三次热力耦合分析,对结晶器锥度进行优化。优化锥度曲线呈抛物线形,总锥度1.88 % /m,在Q195 浇注条件下最大气隙为0.021 mm。优化锥度得到的结晶器内坯壳与结晶器壁间气隙、压力分布合理,能够满足浇注要求。确立的优化方法和分析模型对圆坯结晶器锥度设计具有一定指导意义。
[1]张炯明,张立,杨会涛,等. 板坯结晶器钢水凝固的数值模拟[J].北京科技大学学报,2004,26(2) :130 -134.
[2]刘从港,周书才,杨治立.方坯连铸结晶器凝固传热的有限元数值模拟[J].冶金能源,2009,28(4) :21 -24.
[3]李丰德,王宝峰,李建超,等. 圆坯连铸结晶器锥度的优化设计[J].连铸,2009,(5) :1 -5.
[4]郭旺,刘增勋,朱立光,等.结晶器磨损对铸坯传热的影响[J].钢铁钒钛,2013,34(3) :63 -66.
[5]张海辉,刘建敏,刘增勋,等.方坯结晶器多锥度分析[J]. 钢铁钒钛,2012,33(3)53 -58.
[6]王硕明,朱立光,刘增勋. 方坯高速连铸结晶器锥度优化研究[J].炼钢,2006,22(3) :57 -60.
