基于ADINA的铅芯橡胶支座对渡槽隔震效果的数值模拟
2014-12-21王化翠卢兴旺苑司乐
王化翠,卢兴旺,苑司乐
(1.河海大学水利水电学院,江苏南京210098;2.天津市滨海水业集团股份有限公司,天津300381;3.河南黄河勘测设计研究院北京分院,北京100073)
渡槽的地震安全问题一直都是水工结构抗震领域内关注的焦点之一,由于该类结构上部水体产生的巨大质量及薄壁槽身,使其结构具有不同于一般结构的特殊性,在理论研究、试验研究、设计经验方面缺乏相对成熟的依据[1]。由于渡槽和桥梁在结构形式上十分相似,因此借鉴成熟的桥梁结构减震、隔震研究成果是解决问题的有效途径。传统的工程结构抗震思想是依靠增加结构的刚度,然而对地震作用的抑制并不是十分显著,而且不利于优化结构体型,节约资源。近些年来,隔震技术在实际工程中得到了广泛的应用。在已发生的几次大规模地震中,采用隔震技术的建筑物都达到了预期的目标,体现了良好的抗震性能[2]。铅芯橡胶支座是目前应用比较广泛的一种隔震支座[3],大量实际地震验证了它具有良好隔震效果。鉴此,本文基于有限元程序ADINA建立铅芯橡胶支座以及渡槽隔震结构的数值分析模型,研究铅芯橡胶支座的非线性滞回特性及其对渡槽结构的隔振效果,以期为结构抗震设计提供科学合理的参考依据。
1 研究理论与方法
1.1 铅芯橡胶支座的双线性分析模型
橡胶材料具有超弹性,在荷载作用下发生大变形大位移,表现出强烈的非线性特征。在ADINA程序中有多种材料模型用来模拟橡胶,本文选择常用的Mooney-Rivilin模型研究分析橡胶材料的特性。橡胶材料的应力-应变关系是由应变能密度函数W定义的,对于Mooney-Rivilin模型而言应变能密度函数W是应变不变量I1和I2的函数[4],即

式中:C1和C2是材料力学性能常数。
铅是一种理想的弹塑性材料,应力-应变曲线在屈服前呈弹性关系,屈服后塑性段曲线斜率为零,选择ADINA程序中的Bilinear模型来模拟铅的材料特性。铅的屈服应力较低,在塑性变形条件下还具有较好的疲劳特性,是一种较好的阻尼器,铅芯橡胶支座具有良好的滞回特性,滞回曲线饱满而稳定,滞回曲线近似呈现为双线性行为。日本、新西兰规范均建议采用双线型模型,我国的抗震分析中一般也采用双线型模型进行分析计算[5]。图1为铅芯橡胶支座的双线性模型,图中Qy为铅芯的屈服力,K2为屈服后刚度,K1为屈服前刚度。
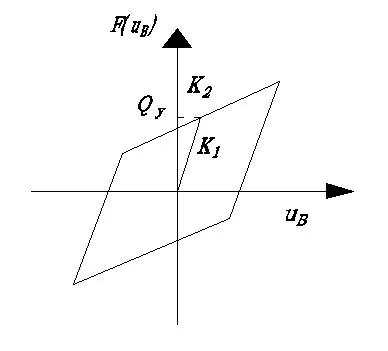
图1 铅芯橡胶支座的双线性模型Fig.1 The bilinear model of lead rubber bearing
1.2 动力分析方法
结构体系的动力平衡方程表示为[6]

式中:{δ},,分别为结构的节点位移、速度和加速度列阵;为地震时地面运动加速度列阵;[K]为系统的整体刚度矩阵;[C]为系统的整体阻尼矩阵;[M]为结构的集中质量矩阵。
时程分析法可以观察到结构在不同时刻下结构的动力响应,并且可以计算非线性动力问题。考虑到铅芯橡胶支座的非线性力学特性,本文在分析地震作用时采用时程分析法。
1.3 ADINA流固耦合理论
渡槽中的水体采用ADINA势流体单元模拟,基于亚音速速度公式的势流体流固耦合有限元方程为[7]:

式中:Δu,Δφ分别为未知的位移矢量增量、势增量;MSS,CSS,KSS,FSS分别为结构的质量、阻尼、刚度矩阵和荷载矢量;MFF为流体质量矩阵;CUU,CFU,CUF,CFF分别为流固耦合界面上固体自身的、固体对流体造成的、流体对固体造成的、流体自身的阻尼矩阵;KUU,KFU,KUF,KFF分别为流固耦合界面上固体自身的、固体对流体造成的、流体对固体造成的、流体自身的刚度矩阵;FU,FF,()S分别为结构边界所受的流体压力、流体连续性方程对应的体积分与面积分。
2 铅芯橡胶支座数值模型的算例验证
2.1 铅芯橡胶支座有限元模型的建立
本文选用文献[4]中的铅芯橡胶支座作为有限元计算的原型,通过有限元计算与试验结果的对比验证本文有限元计算的正确性。铅芯橡胶支座的尺寸是300 mm×300 mm,一共有10层橡胶,每层3.5 mm;9层钢板,每层2.2 mm;上下封板20 mm;中间铅芯直径70 mm。
铅芯在灌入橡胶板和钢板孔时,铅芯的体积比孔的体积大,铅芯被牢固的压入孔中,橡胶支座发生水平位移的时候,铅芯是被迫发生剪切变形的,因此铅芯可以与橡胶板和钢板共节点;在铅芯橡胶支座的实际工作状态中,极少出现橡胶板与薄钢板的剥离现象,两者是在高温高压下粘结形成的,可将橡胶板与薄钢板共节点。在ADINA中使用3D solid单元建立铅芯橡胶支座有限元模型,如图2所示,整个有限元模型一共有15 729个节点,15 360个单元。约束条件为底面固定约束,四周自由。计算方法采用1节介绍的理论与方法进行计算分析。
2.2 有限元分析结果与试验结果的对比
本文仅对文献[4]中的工况一进行模拟,工况一是在0.05 s内施加12 MPa 的均布竖向荷载,保持竖向荷载不变,以0.2 Hz频率施加支座剪切变形γ=100%的水平正弦曲线位移荷载。图3是有限元结果和试验结果的对比图,验证了本文有限元分析程序ADINA数值模拟方法的正确性。
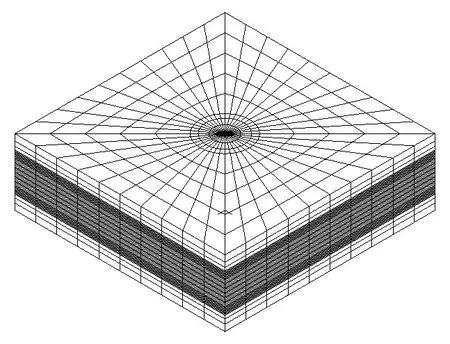
图2 支座的有限元模型Fig.2 3D finite element modal
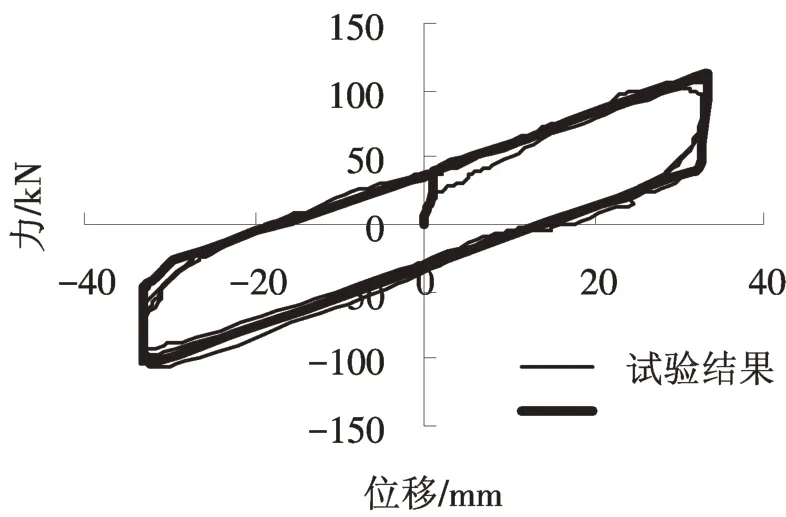
图3 有限元结果与试验结果对比Fig.3 The comparison of the finite element and test results
3 实际工程应用
3.1 工程概况与有限元模型的建立
某渡槽实际工程单跨23 m,槽体底宽6 m,槽体高4.5 m;槽内水体宽5 m,高2.7 m;下部支承结构型式为实体重力墩,由墩帽、墩身、承台组成,槽体与墩台之间共设置4个铅芯橡胶支座,槽身为钢筋混凝土结构。槽体混凝土C50,墩帽混凝土C40,墩体和承台混凝土C25,工程为Ⅱ类场地,设计地震烈度为7度,地震动峰值加速度为0.1 g。为研究隔震支座在地震作用下对渡槽结构的隔振效果,分别建立了该渡槽的有限元隔震模型和非隔震模型。槽体、槽墩、承台采用3D solid单元模拟;水体采用势流体单元模拟,运用ADINA流固耦合算法考虑动水压力;铅芯橡胶支座采用非线性弹簧单元模拟。坐标轴规定:X向为顺槽向,Y为横槽向,Z为竖向。混凝土材料参数:C50弹性模量取33.5 GPa,泊松比取0.167,密度取2 500 kg·m-3,C40 弹性模量取32.5 GPa,泊松比取0.167,密度取2 500 kg·m-3,C25弹性模量取28 GPa,泊松比取0.167,密度取2 500 kg·m-3,混凝土动态弹模参数较静态弹模参数提高30%。铅芯橡胶支座的屈服前刚度为8.26×106N·m-1,屈服后刚度为2.36×106N·m-1,屈服力为159 kN。图4为本文建立的有限元分析模型。

图4 渡槽有限元模型Fig.4 3D finite element modal of aqueduct
3.2 结构自振特性分析
分别对隔震渡槽结构和非隔震渡槽结构进行结构自振特性分析,提取结构的前6阶模态进行分析,两种模型的频率见表1,由表中数据可知,渡槽使用隔震支座时每阶频率均有不同程度的下降,第一阶频率降低了47%,这充分说明隔震支座对降低频率、延长结构周期起到明显的效果。具体延长的多少与结构自身的特性、隔震支座的特性有关,可以通过改变支座力学参数来适当调整结构的周期。从振型方面看,隔震和非隔震结构的振型大体相同,仅在第7阶振型之后发生了变化。
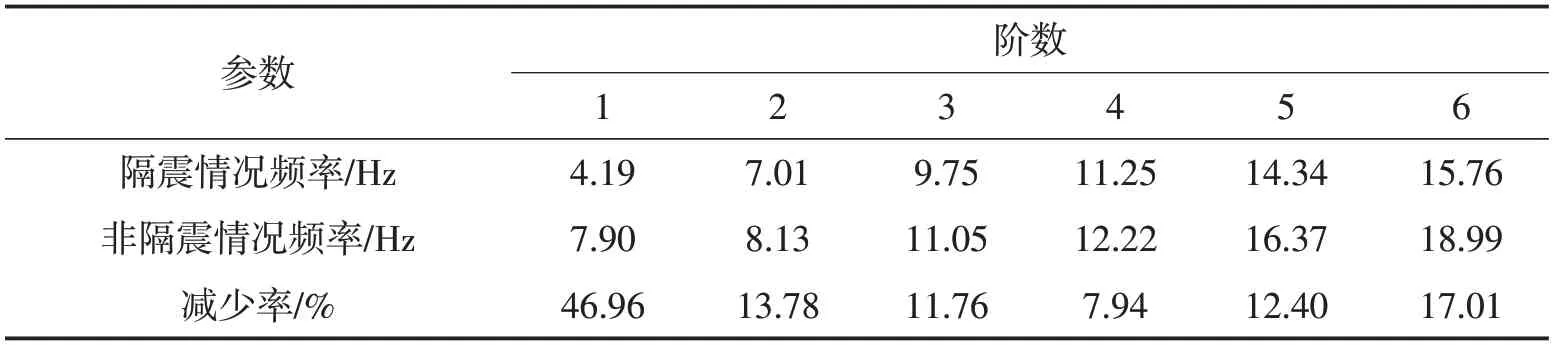
表1 隔震与非隔震两种情况下的频率对比表Tab.1 The frequency comparison in isolated and non-isolated conditions
3.3 地震反应分析
为了研究设置铅芯橡胶支座后渡槽抗震性能,本文运用时程分析法对渡槽进行地震响应分析。对渡槽横向输入7度人工地震波,观察隔震支座对渡槽结构的隔振效果。地震波加速度按照《水工建筑物抗震设计规范》[8]标准设计反应谱拟合人工波,峰值加速度为0.1 g,特征周期Tg为0.2 s,地震持时10 s。本文不计结构静力影响,单独研究地震荷载下的结构动力响应。
表2为正常水位下设置隔震支座与不设置隔震支座时槽体关键部位的地震响应值。图5为具体典型点的位移和应力的时程曲线。从图表中可以看出,设置隔震支座后渡槽绝对位移增大,但渡槽跨中顶部与底部的相对位移、跨中顶部与跨端顶部的相对位移均下降显著。渡槽结构的加速度降幅达56%,第一主应力、正应力也较非隔震时降低50%以上,整个渡槽槽体的地震响应明显下降。以上分析可知:设置隔震支座后结构的地震动力响应得到了很大改善,隔震支座可以明显降低结构的地震响应,从而使结构的抗震性能得到提高。
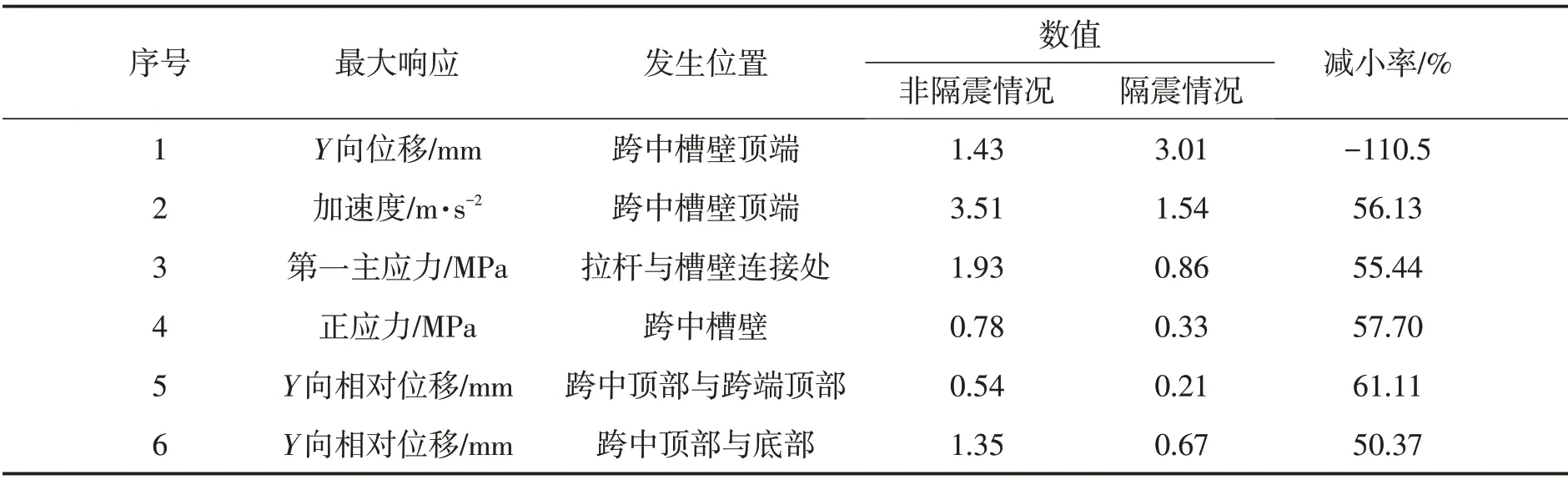
表2 结构地震响应值对比表Tab.2 Comparison of structural seismic response
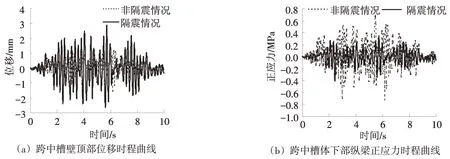
图5 跨中槽体地震响应时程曲线图Fig.5 Time history curves of seismic response
4 结语
1)建立了铅芯橡胶支座的数值模型,采用有限元分析程序ADINA 模拟铅芯橡胶支座的动态力学性能,得到的结果和实验值大体吻合,验证了分析理论和方法的正确性。因此可以利用有限元方法优化铅芯橡胶支座的力学性能,通过改变橡胶厚度、铅芯直径等参数优选隔震支座,而不必进行多次昂贵的试验。
2)分别对设置铅芯橡胶支座的渡槽结构与不设置铅芯橡胶支座的渡槽结构进行时程分析,结果表明:设置隔震支座后,槽体的加速度、应力状况得到了很好的改善,地震响应明显降低,结构的抗震性能得到明显的提高。
3)设置铅芯橡胶支座后槽体位移增大,但仅是铅芯橡胶支座的大变形引起的,槽体跨中顶部与底部的相对位移、跨中顶部与跨端顶部的相对位移显著减少。需要注意加强相邻两跨之间的止水等连接部位设计,可通过设置柔性连接、优化支座力学性能等方式减小相邻垮的影响,保证槽体的安全。
[1]刘云贺,陈厚群.大型渡槽铅销橡胶支座减震机理的数值模拟[J].水利学报,2003(12):98-103.
[2]张艳红,胡晓.大型渡槽隔震研究[J].水利学报,2005,36(11):1307-1313.
[3]熊世树,周正华,王补林.铅芯橡胶隔震支座恢复力模型的分析方法[J].华中科技大学学报,2003,20(02):28-31.
[4]叶志雄,李黎,聂肃非,等.铅芯橡胶支座非线性动态特性的显式有限元分析[J].工程抗震与加固,2006,28(6):53-56.
[5]朱伯龙,张琨联.建筑结构抗震设计原理[M].上海:同济大学出版社,1994.
[6]曹宗杨,张撩军.拱坝-库水动力流固耦合作用的有限元数值研究[J].水电能源科学,2013,31(4):58-61.
[7]中国水利水电科学研究院,电力工业部昆明勘测设计研究院,电力工业部西北勘测设计研究院,等.SL203-97 水工建筑物抗震设计规范[S].北京:中国水利水电出版社,1997.
[8]张汉云,张燎军,李龙仲,等.水电站地面厂房鞭梢效应及抗震分析[J].水电能源科学,2012,30(01):92-126.
[9]高剑平,王斌,刘礼君,等.多层框架结构利用铅芯叠层橡胶支座加层减震分析[J].华东交通大学学报,2009,26(1):1-6.
