一种基于激光雷达的航天器隐藏点测量方法

阮国伟，杨再华，易旺民，刘 涛，范百兴

（1.北京卫星环境工程研究所，北京 100094；2.中国人民解放军信息工程大学，郑州 450092）

0 引言

为保证航天器上安装的敏感仪器、组件及其他设备在飞行期间能够正常工作，在地面安装时应将它们调整到必须的几何精度[1]。目前，航天器的精度检测大多采用基于精测基准镜的光学准直测量方法[2]，即：在被测设备上安装一个精测基准镜，利用经纬仪测量系统测量基准镜之间的相对关系[3]。但是，随着航天器结构布局的愈加复杂，传统的测量方法无法满足一些特殊的测量需求。陶力等使用激光雷达开展了卫星发动机精度测量方法的研究[4]，本文在此基础上将激光雷达的应用拓展到所有隐藏点的测量，并对测量数据进行了分析。

1 测量系统

激光雷达测量系统是一种非接触式球坐标系测量系统。其测量原理是一束聚焦的红外激光投向被测目标，此时在被测目标上产生大量的反射光束，再将入射激光返回雷达所经历的时间与复制的入射激光通过内置且已知长度的光纤所用的时间进行比对，得出被测目标与激光雷达的距离，并根据激光雷达扫描头部光栅码盘测得的球坐标系下的俯仰角EⅠ和偏航角AZ最终得到目标点的坐标：

本文的测试实验采用了美国Metris 公司的MV330 激光雷达，其测量范围30 m，静态测量精度10 µm/m。实验中采用第三方软件Spatial Analyzer（SA）来实现对激光雷达的测量控制以及测量数据的收集和分析。

2 基于激光雷达的隐藏点测量方法

2.1 测量坐标系的建立

在进行设备精度检测前须建立测量坐标系，即建立激光雷达测量坐标系与航天器机械坐标系（一般采用与航天器对接的工艺对接框的坐标系代替）之间的关系。

如图1所示，设A、B、C、D为4 个与航天器机械坐标系位置相对固定的点。通过这4 个公共点的最小二乘拟合，可以得到激光雷达测量坐标系与航天器机械坐标系之间的平移矩阵和旋转矩阵[4]，即完成了测量坐标系的建立。

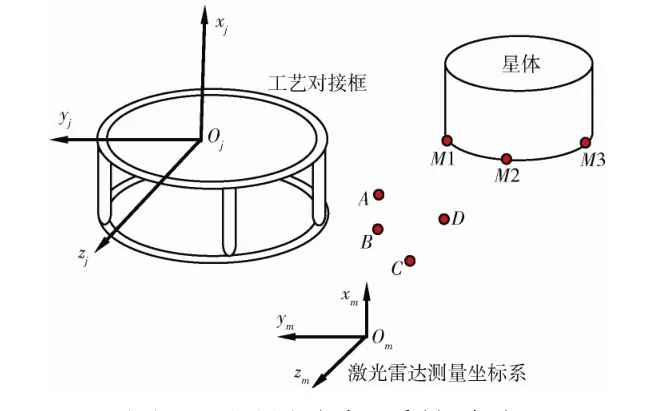
图1 测量坐标系的建立Fig.1 Measurement coordinate system

2.2 高精度反射镜的标定

如图2所示，当被测点A被遮挡时，激光雷达无法直接观测之，可增加反射镜L 进行测量。先固定放置反射镜L，并在镜前固定标定点B用于标定反射镜L 的位置，应保证激光雷达能够同时看到标定点B及其在平面镜中的像B′。

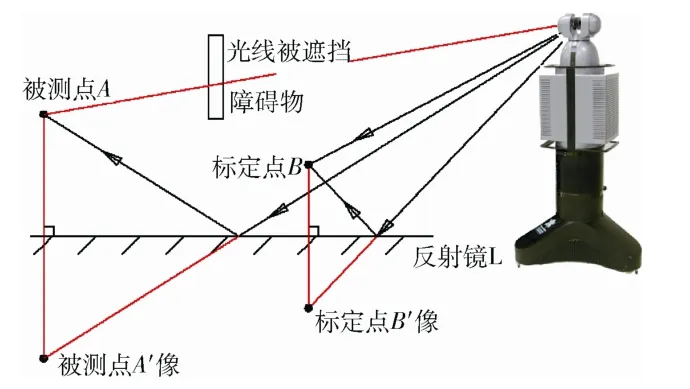
图2 隐藏点测量原理Fig.2 Principle of measuring invisible points

直接测量标定点B在测量系统坐标系下的坐标B(xb,yb,zb)，及其在反射镜中所成虚像的坐标B′(xb′,yb′,zb′)。设平面镜所在平面方程为

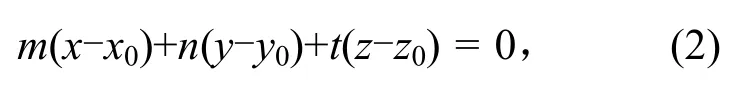
式中：(x0,y0,z0)为平面镜上一点坐标，(m,n,t)为平面镜法线矢量。由B和B′点可以得到平面方程中的未知量：

2.3 隐藏点的测量

标定完成后，直接测量被测点A在平面镜中所成的虚像点A′的坐标(xa′,ya′,za′)。A与A′点镜面对称，因此两点连线的中点也在平面上，且两点连线与镜面法线平行，故得到

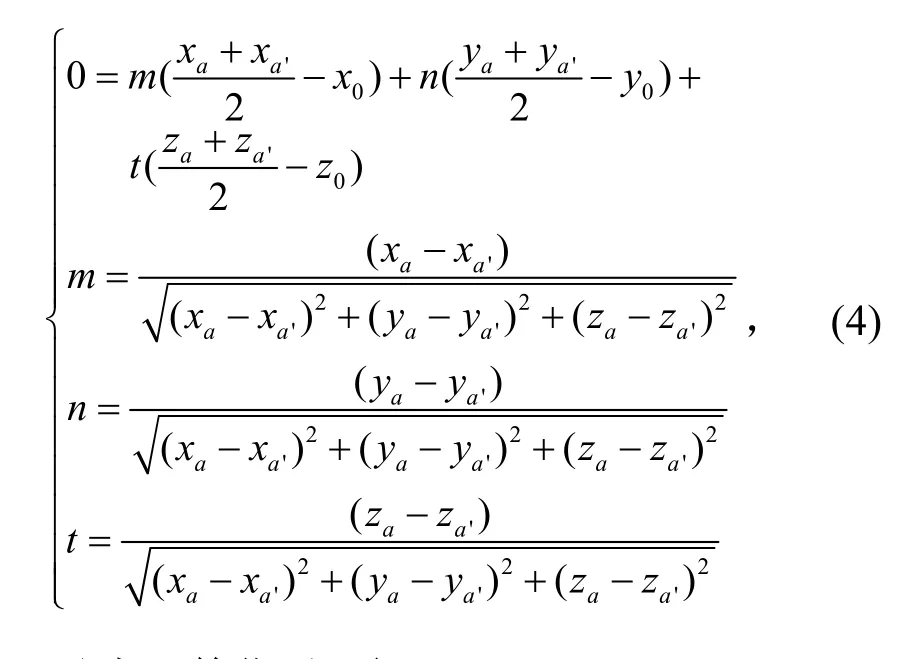
对式(4)简化后可得

式中：k=2mx0+2ny0+2tz0；(m,n,t)、(x0,y0,z0)为标定已知量；(xa′,ya′,za′)为实测值，将这些已知量带入式(5)可以解算得到(xa,ya,za)。因此，对于任何一个被测点，只要可以从反射镜中观测到它的像就可以测算出它的坐标。

3 在航天器发动机装配测量中的应用

装配到航天器上的发动机一般是喷管朝向地面，需要测量发动机喷管的几何轴线相对航天器机械坐标系的角度关系[5]，而喷管内部的点通常无法直接测得。应用激光雷达测量系统，先建立测量坐标系，再放置高精度平面镜并对其位置进行标定，然后利用平面镜反射即可测得发动机喷管内部点的坐标信息（如图3所示），最后生成点云模型（见图4）以获取隐藏点的点云信息。

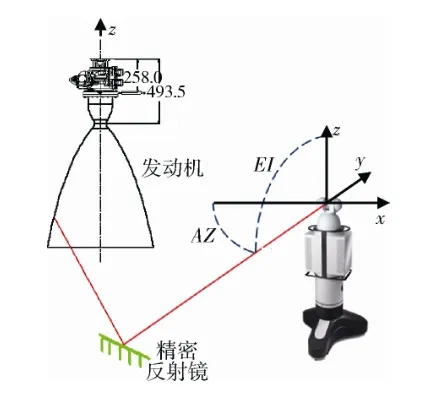
图3 发动机隐藏点的测量Fig.3 Measurement of invisible points for engine

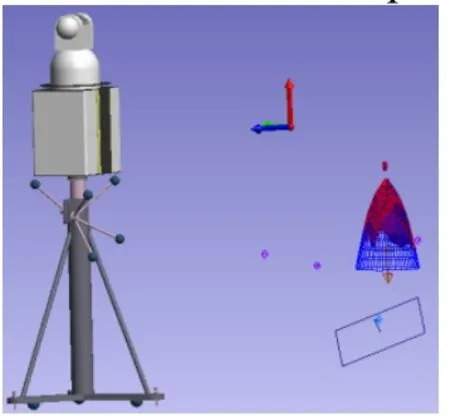
图4 测量结果的点云模型Fig.4 Model of point cloud

在获取的点云模型中选取点坐标，如表1所示。通过最小二乘法拟合得到这些点所在的对称曲面的轴线在航天器机械坐标系下的矢量为(-0.999 89, 0.014 17, 0.003 27)。

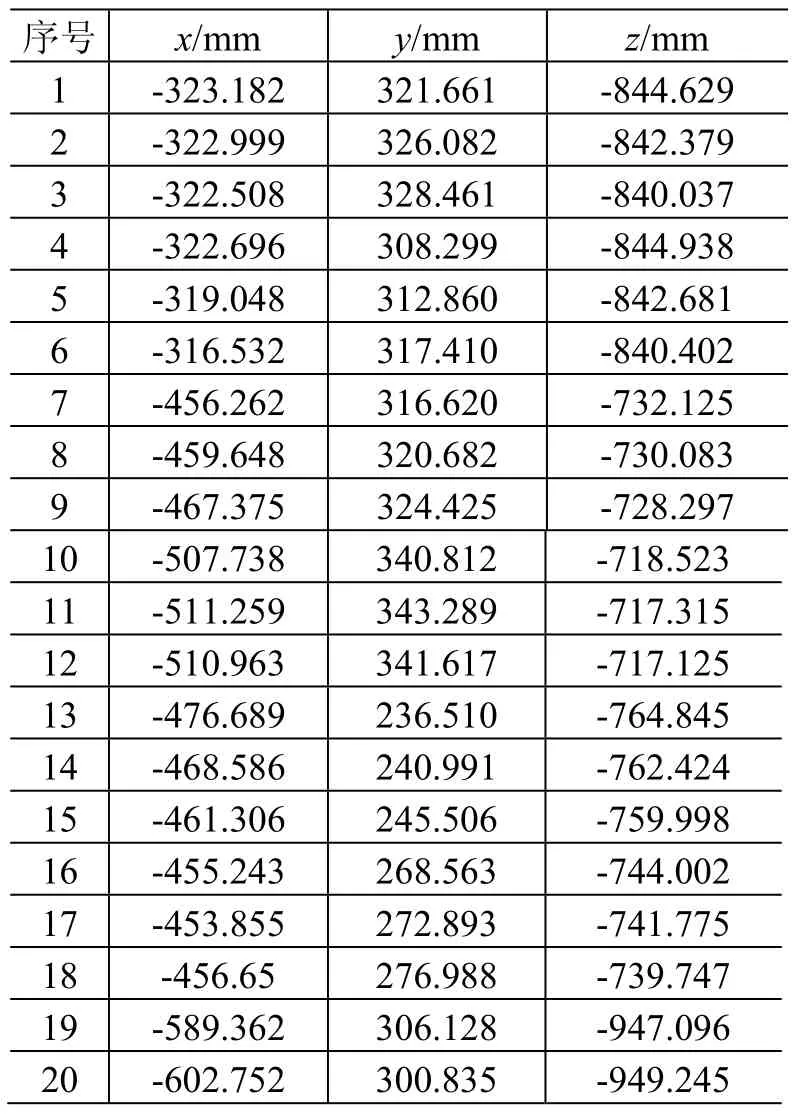
表1 发动机隐藏点的坐标信息Table 1 Coordinates of engine’s invisible points

4 不确定度分析

4.1 仪器测量的不确定度

仪器测量受环境因素的影响，温度梯度、大气抖动、外界振动、被测物的稳定性和强噪声干扰等都会给仪器的测量精度造成不同程度的影响。在高精度测量中，应严格控制这些环境因素并保持温度恒定[6]。在室内环境下，MV330 型激光雷达测量的不确定度（2ρ值）为：u1=0.1 mm。

4.2 坐标系建立的不确定度

通过特征点法建立测量坐标系时，特征点本身的测量误差是坐标系最佳拟合误差的主要来源，通过优化特征点在空间的分布可以最大程度减小单点的测量误差对坐标系拟合的权重。若特征点均匀分布在一个3 m×3 m×3 m 的空间里，多次重复建立坐标系，则可以得到每一次坐标系建立的最佳拟合转换的标准偏差ρ（见表2），其平均值为，则平均值的实验标准差为

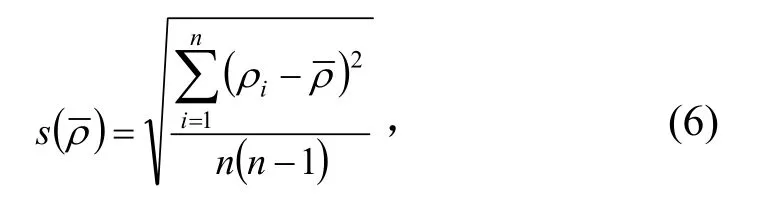
那么，重复测量的标准不确定度为

计算可得u2= 0.025 5 mm。

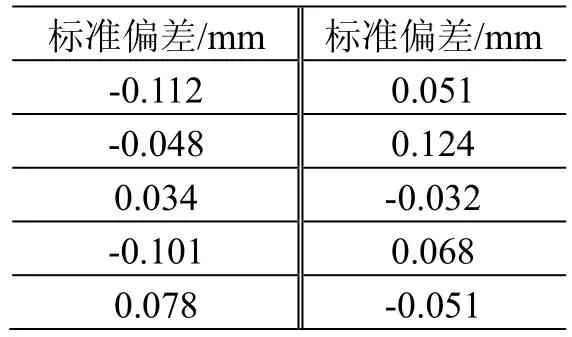
表2 多次重复建立坐标系最佳拟合的标准偏差Table 2 Standard deviations of coordinate fitting

4.3 平面镜反射测量不确定度

平面镜的标定精度直接影响到测量的误差。将工具球放置于平面镜附近，保证能从平面镜里 面看到它的像，对工具球分别使用平面镜反射测量和直接测量，这两者的偏差即为由平面镜测量所带来的偏差，多次测量得到的测量值偏差见 表3。运用4.2 节所列公式可以得到平面镜反射测量不确定度u3= 0.028 7 mm。

表3 平面镜反射测量值与直接测量值的偏差Table 3 Deviations between reflection measurement and direct measurement

4.4 航天器隐藏点测量的标准不确定度

以上分量相互独立，故合成标准不确定度为

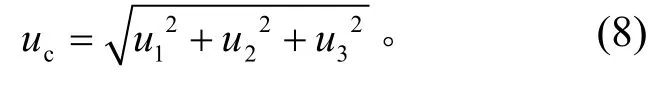
计算可得uc= 0.107 1 mm。

5 结束语

本文提出了一种基于激光雷达的航天器隐藏点测量技术，从理论角度阐述了航天器测量坐标系的建立以及高精度平面镜的标定与测量，并通过实验对该隐藏点测量方法的不确定度进行了分析。结果表明，在保持测量环境稳定的情况下，应用激光雷达进行航天器隐藏点测量的标准不确定度优于0.1071 mm。

（References）

[1]徐福祥, 林宝华, 侯深渊, 等.卫星工程概论[M].北京∶宇航出版社, 2003∶1-307

[2]杨再华.航天器总装精度测量方法分析[J].航天器 环境工程, 2007, 24(6)∶390-392 Yang Zaihua.An analysis of messurement technology in spacecraft assembly[J].Spacecraft Environment Engineering, 2007, 24(6)∶390-392

[3]沈兆欣, 陈晓晖.电子经纬仪测量系统中立方镜坐标系建立技术探讨[J].宇航计测技术, 2006, 26(4)∶73-75 Shen Zhaoxin, Chen Xiaohui.A technology to get coordinate-system of cube-prism in electron-theodolite surveying system[J].Journal of Astronautic Metrology and Measurement, 2006, 26(4)∶73-75

[4]陶力, 杨再华, 阮国伟, 等.基于激光雷达的卫星发动机精度测量方法[J].航天器环境工程, 2013, 30(3)∶328-331 Tao Li, Yang Zaihua, Ruan Guowei, et al.Alignment precision measurement method of satellite engine based on laser radar[J].Spacecraft Environment Engineering, 2013, 30(3)∶328-331

[5]张春富, 唐文彦, 李慧鹏, 等.激光跟踪仪在固体火箭发动机推力线测量中的应用[J].固体火箭技术, 2007, 30(6)∶548-551 Zhang Chunfu, Tang Wenyan, Li Huipeng, et al.Application of laser tracker to thrust line measurement of solid rocket motor[J].Journal of Solid Rocket Technology, 2007, 30(6)∶548-551

[6]吴博海.激光雷达测量仪精度校准方法的研究[J].工业计量, 2010, 20(3)∶1-3 Wu Bohai.Study on calibration method for measuring accuracy of laser radar[J].Industrial Measurement, 2010, 20(3)∶1-3