考虑黏土应变软化的锚板承载力数值分析

周 琪，于 龙

(大连理工大学 建设工程学部，辽宁 大连116024)

很多岩土工程设计涉及到基础抗拔承载力的问题，锚板作为一种经济的、安装快捷的抗拔基础，广泛应用于输电塔及海洋采油平台。在过去的几十年中，前人对锚板的极限承载力问题进行了很多研究，Rowe和 Davis[1]通过有限单元法计算了水平锚板的承载力并提出了土板“立即分离”和“始终黏结”两种作用形式，Merifield 和合作者[2－4]考虑了锚板埋深、锚板倾角、土重、土体抗剪强度、土的非均质度以及锚板的形状对锚板承载力系数的影响，出了锚板承载力的上、下限分析结果。余生兵等[5]采用上限极限分析方法分析了深埋与浅埋锚板在黏土中的承载力系数与破坏面特性。Yu等[6]采用有限元方法研究了锚板倾角、土体非均质度、土重几种因素耦合情况下对条形锚板承载力的影响。这些研究均为静力分析，且并未考虑应变速率和应变软化对黏土强度的影响。Singh等[7]开展了圆形锚板在重塑黏土中的试验，探究了循环荷载周期对锚板位移的影响。Ponniah等[8]针对正常固结黏土中锚板进行了不同平均值和幅值的循环荷载试验，得出锚板在承受平均值和幅值分别为50%和20%的不排水静抗拔力时才会破坏。Andersen[9]利用直剪试验和循环三轴试验来模拟基础潜在破坏面上典型土单元的应力状态，得到静剪应力、循环抗剪强度、循环次数等之间的关系，进而采用循环抗剪强度来评价基础循环承载力。李驰等[10]根据Wang等[11]提出的土的循环强度概念，采用拟静力方法分析了软黏土地基中的单桶基础循环承载力，土的循环强度根据循环小三轴试验结果得出。Zhou和Randolph[12－13]采用数值分析方法探讨了黏土的应变率相关性和应变软化特性对T－bar贯入仪承载力特性的影响，其方法简单直接，参数物理意义明确。本文针对锚板基础，采用有限差分程序FLACV5.0计算锚板的极限承载力系数并与以往结果进行比较来验证数值模型的可靠性，再参考Zhou和 Randolph[13]中采用的应变软化模型计算单调加载情况下锚板承载力曲线。

1 锚板极限承载力系数

1.1 锚板承载力系数结果

一般地，黏土中锚板的极限承载力通常表示为土体不排水抗剪强度的函数[14]:

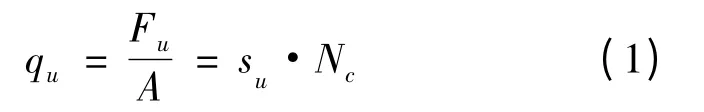
其中:qu为锚板单位面积上的抗拔平均应力;Fu为锚板的抗拔力;A为锚板面积;su为锚板周围土体的不排水抗剪强度;Nc为无量纲的锚板抗拔承载力系数。Nc大小由试验或数值计算结果推得:

为了验证FLAC(Version 5.0)计算锚板承载力的可靠性，计算了不同土重情况下水平锚板与竖直锚板的极限承载力。锚板极限承载力系数计算中采用均匀正方形网格，土体弹性模量和泊松比取为E=250su，υ =0.4。锚板的弹性模量取为 1.25 ×108Pa，比本文强度最高土的弹性模量高1个数量级;锚板泊松比取为0.25。锚板下方与土层之间建立接触面单元，接触面法向刚度和切向刚度均取为5.99×108Pa/m，接触面的抗拉强度取为0，使得土板在受拉情况下立即分离。锚板板宽B=4 m，对于锚板网格宽度b的选择，通过不断试算发现，当网格较大时(b≥B/16)，尽管能得到合理的承载力系数，但是土体的流动机制和剪应变增量云图特征不是很明显。尤其在深埋情况下，因为网格尺寸不够小而使得锚板两侧端的剪切带与环状剪切带之间的非剪切带区域过小，不能清晰表现出深埋局部涡流状的土体流动机制。所以本文计算中选用锚板网格尺寸为b=B/32。采用均匀格式化四边形网格进行计算，如图1所示。

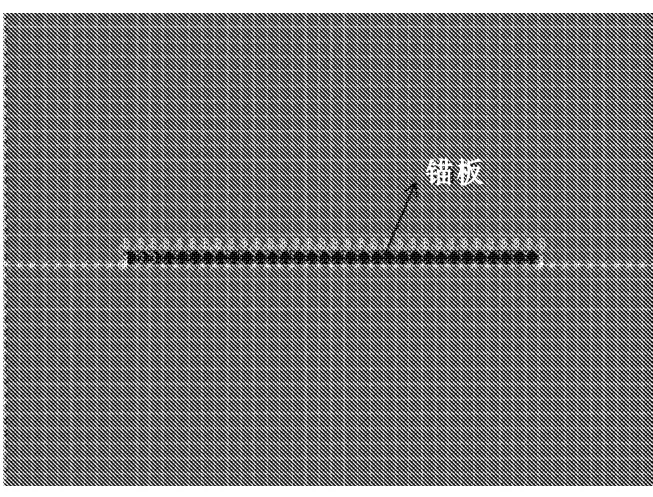
图1 锚板及板周土体单元网格

图2 将本文计算得到的不计土重均质土中不同埋深的水平锚板和竖直锚板的承载力系数与Merifield 等[2－4]的极限分析结果以及 Yu 等[6]的有限元结果进行了比较。其中Merifield的承载力系数值取为上、下限分析结果的平均值。对于水平锚板，当埋深率较小时(H/B＜2)，本文承载力系数结果与Yu的结果吻合较好，在2＜H/B＜5时，本文锚板承载力系数值处于Yu和Merifield的结果之间，而在较大埋深率的情况下(H/B＞5)，本文结果又与Merifield结果吻合较好。对于竖直锚板来说，本文解均比Merifield和Yu的解要稍大一些，承载力数值一般相差0.3左右，占 Merifield和 Yu相应数值的5%左右，本文竖直锚板的结果处在合理范围内。本文水平锚板与竖直锚板的承载力数随不同埋深变化曲线均没有明显的临界值，这是因为在不计土重情况下，土体剪切带均能发展到土体表面，埋深越深剪切带越长，这一点与 Merifield和 Yu的结论也是吻合的。

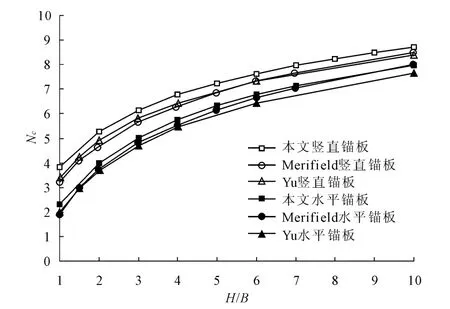
图2 不计土重均质黏土中锚板的承载力系数比较

图3 给出了均质土中不同埋深、不同上覆土重的竖直锚板承载力系数值。在上覆土重应力水平γH/su较小的情况下，即没有达到临界值之前，锚板的承载力系数Nc等于土体自重应力水平加上不计土重土板立即分离的锚板承载力系数(叠加法)，即

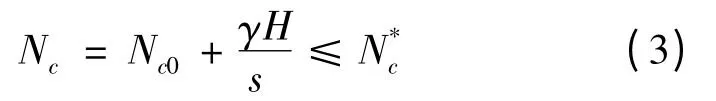
式中:Nc0是不计土重土板立即分离的锚板承载力系数;γ为土重度;N*c是极限承载力系数。

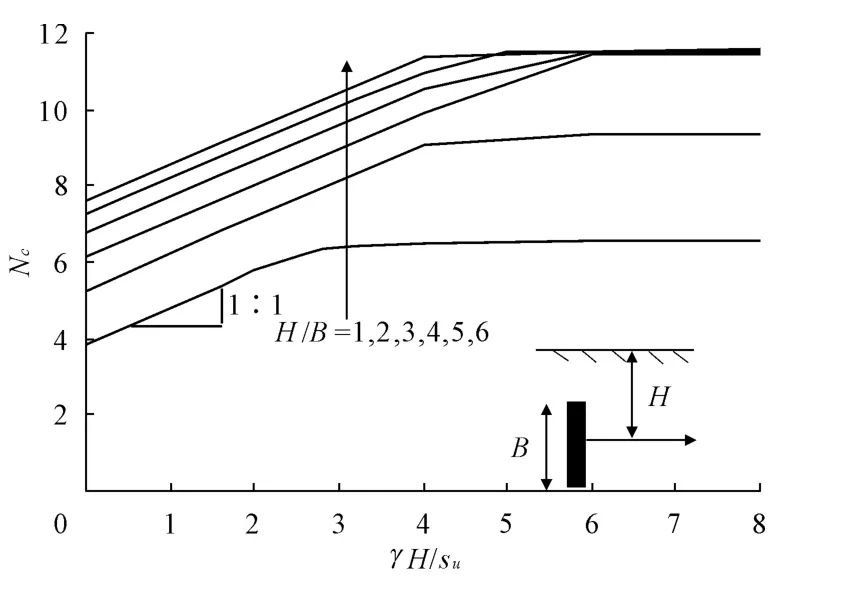
图3 上覆土重对锚板承载力系数的影响

图3 中对于 H/B=1和2的情况，锚板承载力系数在γH/su分别为3.2和6时，分别达到极限值6.41和9.38，此后不再随上覆土重应力水平变化而变化。对于 H/B=3、4、5和6时，锚板在超过临界埋深后均呈深埋破坏形式，土体破坏机制为完全局部回流机制，锚板承载力系数达到最大值11.54，与Merifield下限分析结果10.47相差9%左右，同 Yu的有限元计算结果11.59相差仅仅0.4%。在锚板承载力系数随土重变化阶段，曲线斜率均为1∶1，超过一定上覆土重后，锚板承载力系数不再随上覆土压力变化而呈水平段，这与已有文献分析结果相吻合。

1.2 典型的土体破坏流动机制

对于典型浅埋水平锚板(H/B=1，γH/su=1.28，以下简称为 H/B=1)，典型土的流动机制如图4所示。相应地，图5给出了在锚板承载力系数计算已达到完全塑性段时某两计算步之间的剪应变增量等值线图。可以看出，土体流动几乎竖直向上延展到土体表面，剪切带从锚板两端边缘持续向上发展到表面，这种典型浅埋破坏模式的土体流动机制与剪应变发展模式与已有结果(Merifield等[2];Yu 等[6])吻合。

图6、图7给出典型深埋水平锚板(H/B=6，γH/su=7.68，以下简称为 H/B=6)局部土体破坏流动机制的土体位移矢量图和相应的承载力计算已达到完全塑性段时的某两计算步剪应变增量等值线图，可以看出，土体破坏机制呈局部回流机制，剪切带呈环形。这些都与 Yu 等[6]、Merifield 等[2－4]的结果一致。从上述锚板承载力系数及典型土体流动机制来看，利用FLAC有限差分程序计算锚板承载力可以得到比较可靠的结果。

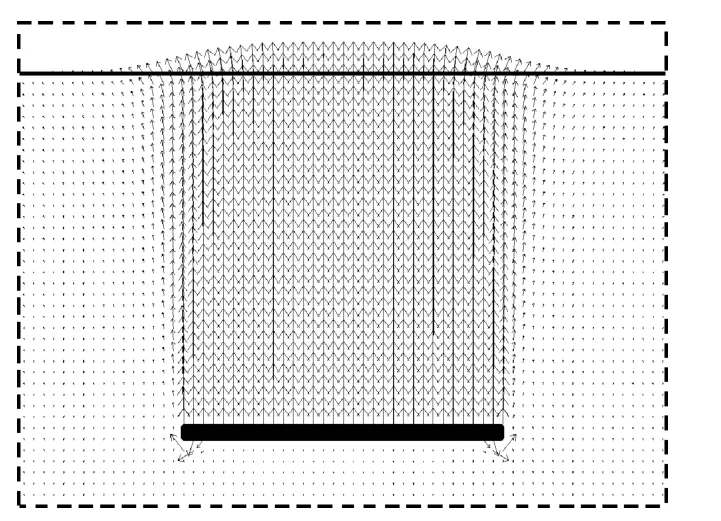
图4 浅埋锚板土体位移矢量图(H/B=1)

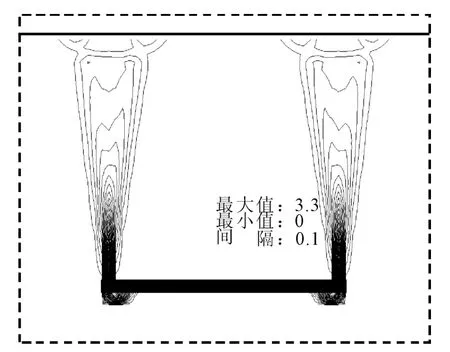
图5 浅埋锚板剪应变增量等值线云图(H/B=1)

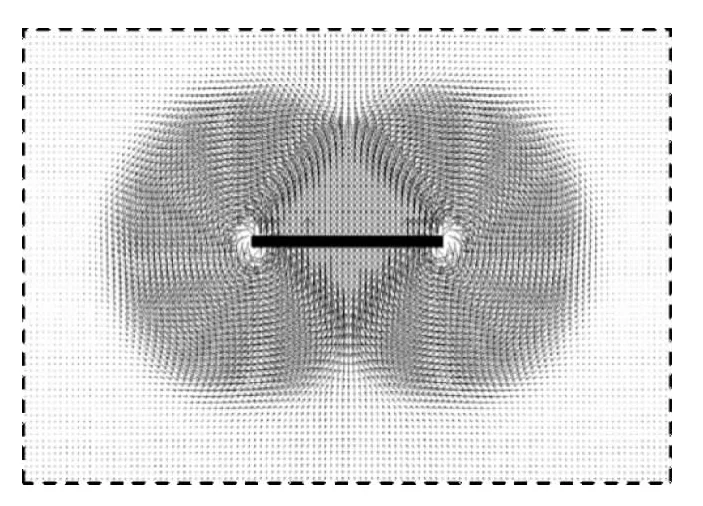
图6 深埋锚板土体位移矢量图(H/B=6)

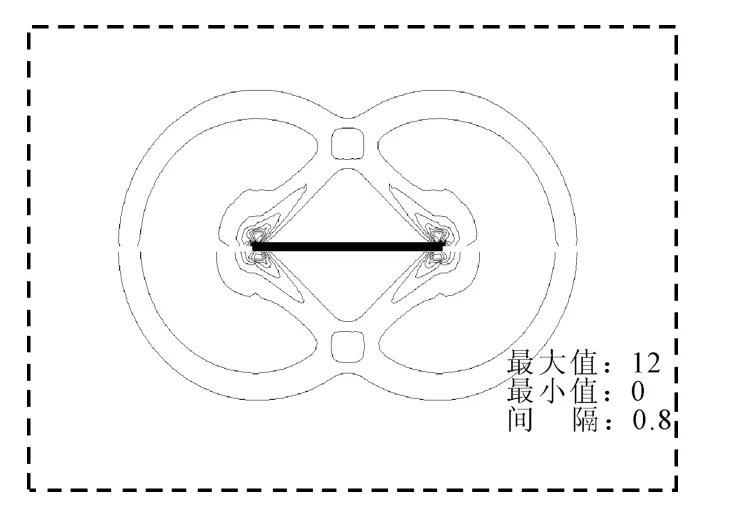
图7 深埋锚板剪应变增量等值线云图(H/B=6)

2 锚板承载力软化计算

2.1 应变软化模型

锚板在波浪力等循环荷载作用下会因为对土的不断扰动而使塑性剪应变不断积累导致承载力软化。为了利用贯入仪来触探土的强度，Zhou和Randolph[12－13]对土体的应变率相关性以及应变软化特性进行研究，其中应变率相关性和应变软化模型用以下方程来表示:

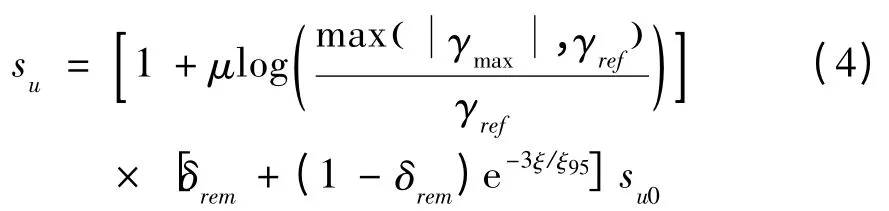
式中乘号前后两部分分别代表高应变率引起的土体强度的增加和应变软化引起的强度的减少。本文仅考虑第二部分应变软化函数来进行数值分析。乘号前部分中γref表示参考剪应变。式(4)中第二部分su0是没有任何软化发生的初始抗剪强度，δrem是完全重塑后的土体抗剪强度与未扰动土的抗剪强度的比值(即为敏感度St的倒数)，ξ表示的是高斯点的累积塑性剪应变绝对值，不计弹性剪应变，这点与FLAC中的应变软化模型是一致的。ξ95代表的是土进行了95%的扰动程度之后的ξ值，此值也反应土的塑性。尽管FLAC中的应变软化模型计算累积塑性剪应变的方式[15]与前述模型有差别，但是不影响计算结果的合理性。计算采用参数ξ95=5，δrem=0.7，其对应的土的抗剪强度su值随ξ变化的曲线如图8所示。

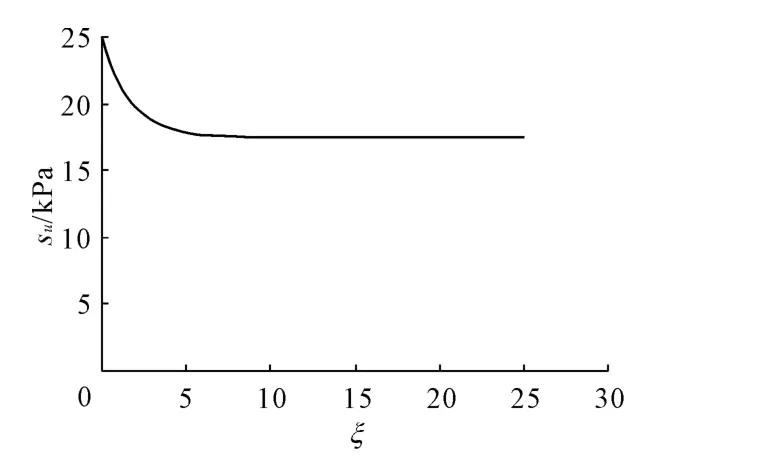
图8 土的抗剪强度随塑性剪应变变化曲线(ξ95=5，δrem=0.7)

2.2 锚板承载力应变软化分析

本部分以板宽B=4 m，土重度γ=8 kN/m3为例，计算了深埋、浅埋水平锚板两种工况，即H/B=1，γH/su=1.28 与 H/B=6，γH/su=7.68(以下仅用H/B=1和H/B=6表示)，其对应的不计软化承载力计算中得到的剪应变增量云图和土体位移矢量图已由上文图4～图7给出。土体的初始抗剪强度su0均取为25 kPa。图9将H/B=1的计算工况中利用摩尔库伦模型计算得到的无软化承载力 －位移曲线与利用应变软化模型计算得到承载力位移曲线进行了比较。其中横坐标和纵坐标都进行了无量纲化处理。从图9中可以看出，无软化锚板承载力系数为Nc=3.60。考虑软化时锚板峰值承载力系数为Nc=3.51，比不考虑软化时稍小;残余承载力系数为 Nc=2.93。

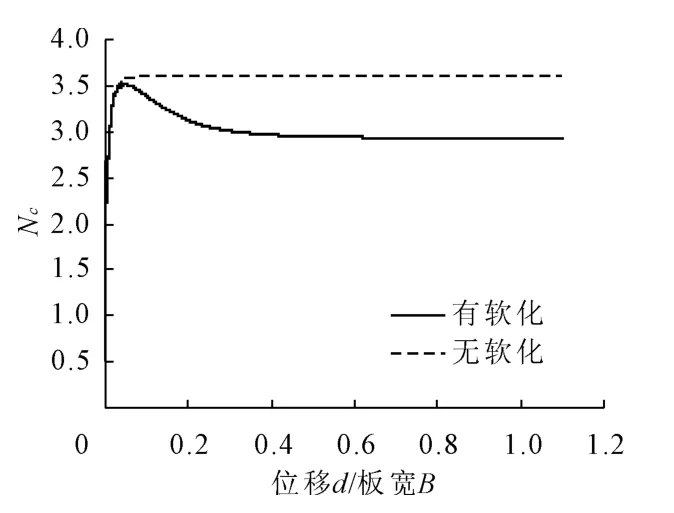
图9 摩尔模型和应变软化模型计算的锚板承载力比较(H/B=1)

土单元的抗剪强度在完全扰动后会达到初始抗剪强度su0的70%(δrem=0.7)，而实际软化后残余承载力系数是无软化承载力系数的81.6%，这是因为锚板的承载力由两部分提供(公式(3)):剪切带上土的剪力之和和锚板埋置深度的上覆土重应力水平。对于本算例，埋深率H/B=1，土重应力水平γH/su=1.28，若根据图 1 计算结果取 Nc0=2.3，则根据叠加法式(3)得不计软化情况下(su=25 kPa)的承载力系数应为Nc=3.58，这同FLAC计算结果Nc=3.60基本吻合。若考虑完全软化，应变软化发生在剪切带上的土单元中，其他土体单元并不发生软化，式(2)计算承载力系数Nc的su和计算土重应力水平的 su应仍取25 kPa，而 Nc0的取值应折减为不计软化Nc0的0.7倍。因此，按式(3)，完全软化时承载力系数应为 Nc=2.89，数值计算结果 Nc=2.93与之非常接近。详细计算结果列于表1。

表1 锚板承载力构成(H/B=1和H/B=6)

对于H/B=6工况，土体流动机制为局部回流机制(图6，图7)，此时锚板极限承载力系数不再受上覆土重的影响，图10将分别利用不计软化和考虑软化模型计算得到的锚板承载力系数进行了比较。无软化时，锚板极限承载力系数由公式(3)所得结果为11.55，与数值计算直接得出的系数11.54基本一致(见表1)。考虑软化时，锚板峰值承载力系数大小为Nc=11.38，约占无软化时峰值承载力11.54的98.6%;残余承载力系数 Nc=8.23，软化全部发生在局部涡流状的剪切带上的土单元中，理论上完全软化时的残余承载力系数Nc是无软化时锚板极限承载力系数的0.7倍，即为8.08，与计算值8.23相差不大(见表1)。

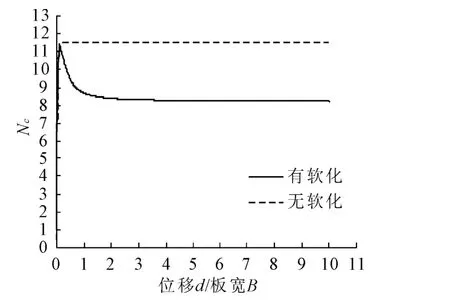
图10 不计软化和考虑软化模型计算的锚板承载力系数比较(H/B=6)

3 结论

(1)采用FLAC2D中的摩尔－库伦模型计算了不计土重土板立即分离情况水平锚板和竖直锚板的承载力系数以及计土重土板立即分离的上覆土重对竖直锚板承载力系数的影响，与已有文献结果吻合较好。

(2)利用FLAC2D中的应变软化模型对典型的低应力水平(H/B=1)和高应力水平工况(H/B=6)进行锚板承载力软化计算。软化计算结果可靠，高应力水平工况需要更多的上拔位移来达到锚板残余承载力。FLAC中的应变软化模型能够较好的反映土的软化特性。

[1]Rowe R K，Davis E H.The behaviour of anchor plates in clay[J].Geotechnique，1982，32(1):9-23.

[2]Merifield R S，Sloan S W，Yu H S.Stability of plate anchors in undrained clay[J].Geotechnique，2001，51(2):141-153.

[3]Merifield R S，Lyamin A V，Sloan S W，et al.Three-dimensional lower bound solutions for stability of plate acnhors in clay[J].Journal of Geotechnical and Geoenvironmental Engineering，2003，129(3):243-253.

[4]Merifield R S，Lyamin A V，Sloan S W.Stability of inclined strip anchors in purely cohesive soil[J].Journal of Geotechnical and Geoenvironmental Engineering，2005，131(6):792-799.

[5]余生兵，黄茂松.基于上限法的条形锚板抗拔承载力分析[J].岩土力学，2010，31(增 2):160-163.

[6]Yu Long，Liu Jun，Kong Xianjing，et al.Numerical study on plate anchor stability in clay[J].Géotechnique，2010，61(3):235-246.

[7]Singh S P，Ramaswamy S V.Influence of frequency on the behaviour of plate anchors subjected to cyclic loading[J].Marine Gerresources ＆ Geotechnology，2008，26(1):36-50.

[8]Ponniah D A，Finlay T W.Cyclic behaviour of plate anchors[J].Canadian Geotechnical Journal，1988，25(2):374-381.

[9]Andersen K H，Rosenbrand W F，Brown S F.Cyclic and static laboratory tests on drammen clay[J].Journal of the Geotechnical Engineering Divisioon，1980，106(5):499-529.

[10]李 驰，王建华，刘振纹.软土地基单桶基础循环承载力 研 究[J].岩 土 工 程 学 报，2005，27(9):1040-1044.

[11]Wang J，Liu Y，Xing Y，et al.Estimation of undrained bearing capacity for offshore soft foundations with cyclic load[J].China Ocean Engineering，1998，12(2):213-222.

[12]Zhou H，Randolph M F.Computational techniques and shear band development for cylindrical and spherical penetrometers in strain-softening clay[J].International Journal of Geomechanics，2007，7(4):287-295.

[13]Zhou H，Randolph M F.Resistance of full-flow penetrometers in rate-dependent and strain-softening clay[J].Géotechnique，2009，59(2):79-86.

[14]于 龙.三维RITSS大变形有限元方法及其基础刺入破坏和锚板承载力问题中的应用[D].大连:大连理工大学，2008.

[15]Itasca Consulting Group，Inc.Fast Language of Continua in Dimensions Version 5.0，User’s Manual[M].Itasca Consulting Group，Inc.，2005.