四足机器人节律柔顺行走控制

邵雪松，黄奇峰，蔡奇新，刘 建，王 伟

（1.江苏省电力公司电力科学研究院，江苏 南京210019；2.中国科学院自动化研究所，北京100190）

0 引 言

中枢模式发生器是由多个神经元组成的振荡网络，通过神经元之间的相互激励和抑制，产生动物所需的节律运动信号，这是一种低级神经中枢的自激行为，存在于动物的脊椎和胸腹神经节中，常见的运动方式如呼吸、咀嚼、游泳、行走、飞行等。通过分析自然界动物的节律运动规律，生物控制越来越多的被应用于机器人控制之中，形成了仿生控制方法，主要利用非线性振荡器网络建立中枢模式发生器模型，模拟动物的神经控制机理［1，2］。

神经元振荡器是中枢模式发生器的基本组成单元，许多学者曾建立多种振荡器模型。这些模型不尽相同，但是具有节律运动控制所需的共同特点：①抗干扰能力强，当出现外界干扰信号时，振荡器能够保持输出信号的稳定。②能够形成振荡器网络，产生相位关系锁定的节律信号。③振荡器输出信号的频率、幅值等参数可调［3－6］。虽然仿生控制方法无需考虑四足机器人本体及其运动环境的模型，但是所产生的节律信号使四足机器人足端与地面之间的碰撞力发生突变，很难从真正意义上模仿四足动物的柔顺行走。此外，在中枢模式发生器的建立过程中，往往需要针对每个关节建立振荡器单元，振荡器网络模型十分复杂；少数学者开始从中枢模式发生器模型入手，分析每条腿上各关节之间的节律运动关系，利用同一振荡器单元控制一条腿上的各关节运动［7］，从而简化整体振荡器网络。

针对上述问题，本文首先建立基于Hopf振荡器模型的四足机器人运动控制器，分析参数变化对模型输出的影响，增加单个振荡器模型的输出变量个数，利用单个神经元控制包括髋关节和膝关节在内的单腿运动，改变各神经元之间的耦合作用变量，实现对称步态和非对称步态行走。分析四足机器人与地面之间碰撞力的变化特点，提出柔顺性评估指标，改进中枢模式发生器模型，调整节律信号输出规律，实现四足机器人节律柔顺行走。

1 节律运动突变碰撞力分析

1.1 四足机器人虚拟样机与运行环境建模

本文首先根据四足哺乳动物的外形条件和运动方式，建立四足机器人虚拟样机模型，如图1所示。样机由身体body、髋关节连杆hip link、大腿thigh、小腿shank 和足foot组成，每条腿有3 个自由度，分别为膝关节俯仰自由度knee pitch、髋关节俯仰自由度hip pitch和髋关节偏摆自由度hip yaw，其中，髋关节偏摆关节连接身体和髋关节连杆，髋关节俯仰关节连接髋关节连杆和大腿，膝关节连接大腿和小腿，小腿和足端采用固定连接。虚拟样机长1050 mm，宽720 mm，高660 mm，大腿和小腿长度均为350 mm，髋关节连杆长度为85mm，总重量为50kg，其中身体20kg，髋关节连杆1.5kg，大腿3.5kg，小腿2.0kg，足0.5kg。同时，为四足机器人设定初始关节角，髋关节俯仰自由度初始角θ0＝30°，膝关节初始角φ0 ＝60°，以初始位置为起点，设定各关节转动方向与行进方向一致时为正方向。

仿真过程中，机器人不可避免的会与运行环境发生交互，同时机器人各连杆关节也会产生约束力，包括足端与地面之间的碰撞力、摩擦力以及关节运动副中的摩擦力。在ADAMS仿真环境中，这些变量计算方法和参数设置的合理性，决定对真实四足机器人运动的模拟程度，将对四足机器人的正常运行和柔顺行走控制研究起到重要作用。为了使仿真研究具有较强的可比性，本文对相关参数统一设置。

图1 四足机器人虚拟样机

对于机器人足端与地面之间碰撞力的计算，选用系统中的Impact冲击函数法，这种方法所定义的碰撞力由2部分组成，分别为由2个实体的相互穿透而产生的弹性力和由实体之间的相对运动而产生的阻尼力。对于冲击函数法的计算参数，选择接触刚度 （stiffness）＝10，接触力指数（force exponent）＝2.2，阻尼系数 （damping）＝10，最大穿透深度 （penetration depth）＝0.1mm。对于机器人足端与地面之间摩擦力的计算，选用系统中的Coulomb库仑法，参数设定为静摩擦系数 （static coefficient）＝0.5，动摩擦系数 （dynamic coefficient）＝0.3，静滑移速度 （stiction transition vel）＝100 mm／s，动滑 移速度 （friction transition vel）＝1000 mm／s。在机器人关节旋转副上添加摩擦力，其中，静摩擦系数 （mu static）＝0.5，动摩擦系数（mu dynamic）＝0.3，摩擦反作用力臂 （friction arm）＝1.0，弯曲反作用力臂 （bending reaction arm）＝1.0，静态滑动速度 （stiction transition velocity）＝0.1 mm／s，静摩擦 时 旋 转 副 最 大 变 形 （max stiction deformation）＝0.01mm。

1.2 基于Hopf振荡器的中枢模式发生器建模

Hopf振荡器是一种非线性振荡器模型，输出信号的幅值、频率和相位可调，稳定性高，锁相特性强，具有较强的抗干扰能力，能够实现反馈调节。更为重要的是在同一信号周期中，上升阶段和下降阶段的频率可以灵活调节，这种分段频率可调特性有利于模仿动物的节律运动行为［8，9］。另外，Hopf振荡器模型简洁，容易理解，被广泛用于机器人节律运动控制中。Hopf振荡器数学模型可表示为

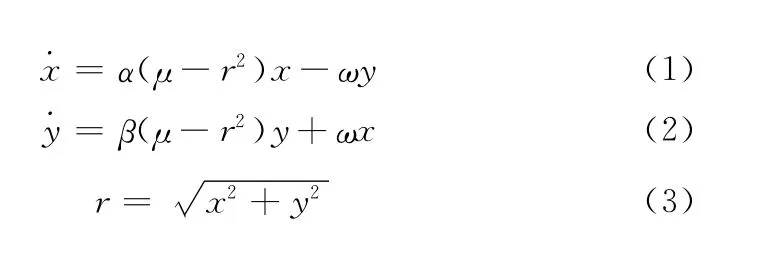
在本文四足机器人柔顺行走控制中，锁定髋关节偏摆自由度，只针对四足机器人直线行走时的运动特性建模分析。在此，将四足机器人的每条腿作为一个单元，用一个Hopf神经元振荡器来表示，不同腿的神经元之间通过耦合连接相互兴奋或抑制，产生具有一定相位锁定关系的输出信号，这些信号可用来控制各腿的关节运动，通过各腿之间的协调运动产生不同的四足机器人行走步态。

Hopf振荡器的输出信号x 可作为四足机器人各髋关节俯仰自由度的控制信号，信号y 反映信号x 的变化情况，且幅值和变化趋势与信号x 保持一致，因此，可对信号y进行半波截取，作为各膝关节俯仰自由度的控制信号。通过对振荡器输出信号的整合，使单个振荡器控制单条腿的关节运动，而无需像传统方法一样对膝关节单独设置振荡器单元或半波函数，避免了中枢模式发生器模型繁琐、膝关节控制信号不连续以及膝关节与髋关节信号不一致的问题。

在对角小跑步态 （Trot）、踱步步态 （Pace）、跳跃步态 （Bound）等对称步态模型中，将Hopf振荡器输出信号y 作为各腿之间的耦合作用信号。对于慢走步态 （Walk），每个步态周期中腿的摆动相时间与站立相时间比为1∶3，相邻摆动腿之间相位相差为π／4，而Hopf振荡器锁相特性强，耦合关系严重，对称步态下的神经元相互作用关系较弱，无法形成所需的慢走步态相位关系。针对此问题，本文对对称步态下的中枢模式发生器模型进行改进，将Hopf振荡器输出信号x取代输出信号y作为神经元之间的耦合作用变量，用以构建非对称步态拓扑结构。

中枢模式发生器模型如下

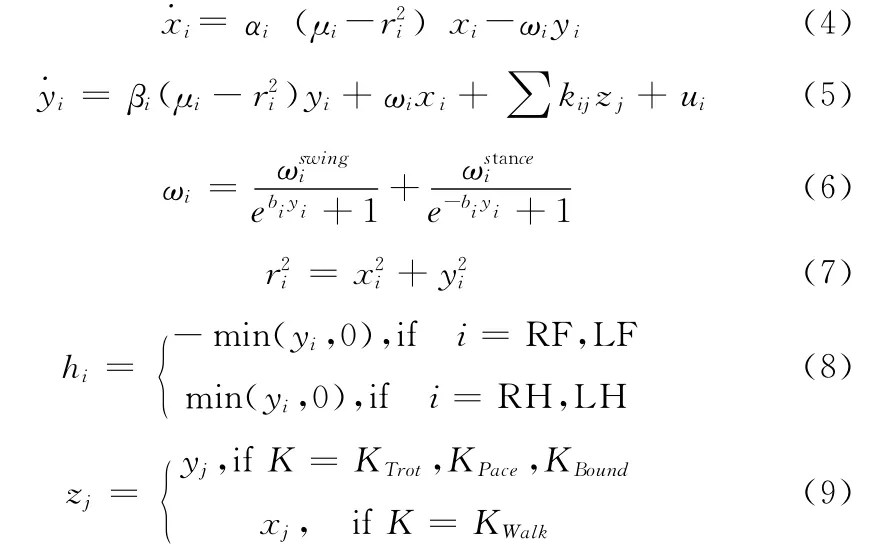
其中，RF代表四足机器人右前腿，LF 代表左前腿，RH代表右后腿，LH 代表左后腿，i，j＝RF，LF，RH，LH，xi为第i个神经元在髋关节俯仰自由度的输入，hi为第i 个神经元在膝关节俯仰自由度的输入，zj为第j 个神经元在第i个神经元上的作用变量，为第i 个神经元输出信号的幅值，yi和ri为第i个神经元的中间变量输出，αi和βi 为第i个神经元的收敛速度控制变量，kij为第j 个神经元作用于第i个神经元的权值系数，μi 为作用于第i 个神经元的上层输入信号或者反馈信号，bi为第i 个神经元的频率调整常数，ωi为第i个神经元的振荡频率，由2部分决定：ωstancei和，表示第i个神经元所在腿的站立相频率，对应于Hopf振荡器输出信号x 的下降阶段；ωswingi表示第i 个神经元所在腿的摆动相频率，对应于Hopf振荡器输出信号x的上升阶段；KTrot、KPace、KBound、KWalk分别为Trot步态、Pace步态、Bound步态和Walk步态的耦合矩阵。

1.3 突变碰撞力分析

四足机器人行走过程中，腿的抬起与落下会形成足端与地面的碰撞，而中枢模式发生器控制四足机器人运动会引起足端与地面的碰撞力突变，这种较大的突变碰撞力会对机器人本体产生冲击，使机器人运动不连续，柔顺性降低。本文以对称步态中的对角小跑步态 （周期为1s，步幅为10°）和非对称步态中的慢走步态 （周期为1.25s，步幅为10°）为例对碰撞力突变问题进行分析。

对角小跑步态中，选择左前腿运动状态进行分析，碰撞力如图2所示；慢走步态中，选择右前腿运动状态进行分析，碰撞力如图3所示。在每一个步态周期中，髋关节从－10°转动到10°，对应于大腿从后极限位置 （PEP 点）运动到前极限位置 （AEP点），膝关节从0°转动到10°再转回0°，对应于小腿从后极限位置 （PEP 点）运动到前极限位置 （AEP 点）再回到后极限位置 （PEP 点），此时，腿从摆动相进入站立相，在摆动相结束、站立相开始的时刻，足端与地面发生碰撞，碰撞力急剧上升，这种突变碰撞力会引起身体姿态发生突变。分析四足机器人身体质心（COM）在垂直方向上的运动轨迹 （图4、图5所示）可以看出，机器人足端落地引起碰撞力突变的同时，对机器人整体的运动状态也会产生影响，最直观的表现为身体质心轨迹在垂直方向上的剧烈变化。此外，随着运动速度的提高，足端触地时的速度增加，碰撞时间变短，突变碰撞力进一步增大，身体姿态变化更加剧烈。

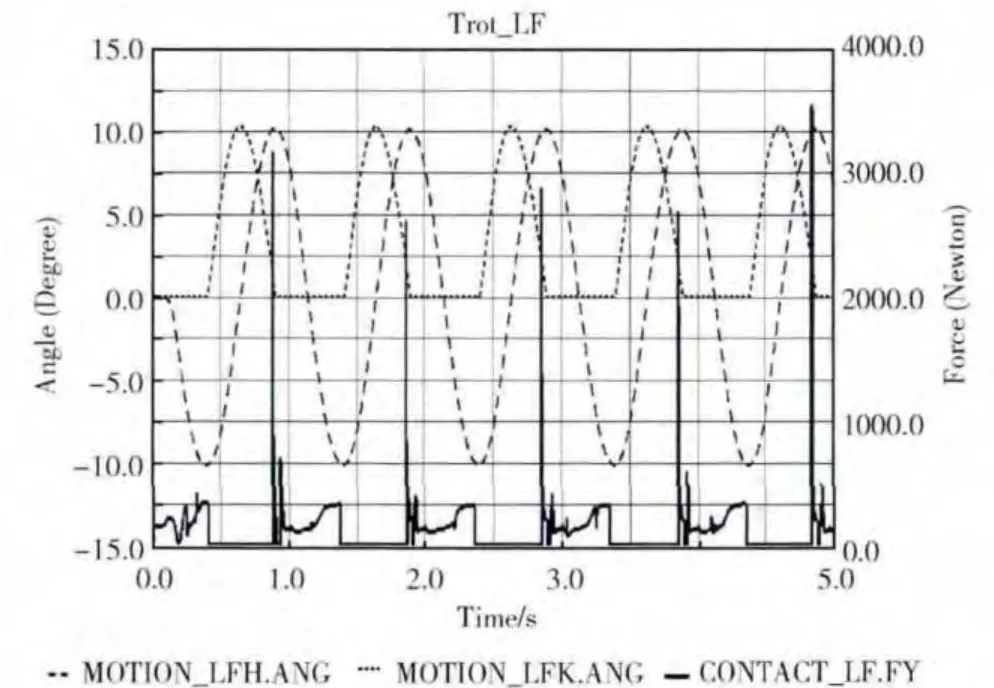
图2 Trot步态左前腿关节运动轨迹与垂直碰撞力关系

图3 Walk步态左前腿关节运动轨迹与垂直碰撞力关系

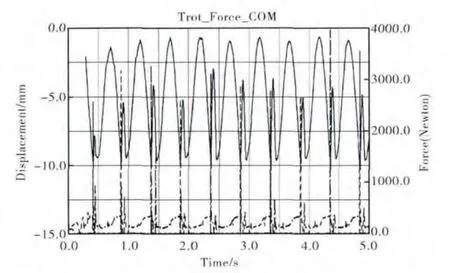
图4 Trot步态碰撞力与四足机器人质心变化关系

图5 Walk步态碰撞力与四足机器人质心变化关系

2 柔顺行走控制

四足机器人节律运动控制源于模仿自然界动物的神经元模型控制，因控制方式简单、控制步态多变而被广泛研究，但是动物的运动是由各级神经组织 （包括各级神经中枢以及全身神经末梢等）相互作用、身体骨骼肌肉组织相互配合的整体复杂神经系统所控制的，在运动过程中决策高效可靠、姿态调整灵活多变、步态选择合理、运动方式柔顺［10］。中枢模式发生器控制作为一种基于模拟低级神经中枢作用机理的控制结构，因缺乏各级神经中枢的整体决策、神经末梢的反馈感知、肌肉组织的相互配合而存在许多问题，其中最为典型的是柔顺性问题。因此，本文以所建立的中枢模式发生器为基础，研究四足机器人节律运动柔顺行走控制问题。

2.1 柔顺行走控制策略

四足机器人节律运动中的较大突变碰撞力来源于2个方面：第一，节律运动没有考虑环境的反馈信息，即没有通过反馈调节与环境进行交互，无法感知足端与地面的相对位置，不能做到及时调整；第二，节律运动考虑的只是四足机器人各关节之间的角度变化以及相位顺序情况，没有涉及机器人本身的运动学动力学模型，在运动过程中只要求各关节运动到指定位置即可，没有考虑速度、加速度变化与运动状态之间的关系，从而在落地过程中足端与地面之间产生瞬间的较大突变碰撞力。自然界四足动物与环境交互依靠的是全身感知系统、上层决策系统、以及运动经验等，而非某种单一传感器；其次，基于中枢模式发生器的节律运动控制器模型参数之间耦合作用强，参数调节复杂，一个参数的变化往往会引起其它函数特性的改变；另外，四足机器人足端与地面之间的瞬时碰撞力变化较快，一方面没有合适的传感器用于有效检测，另一方面，中枢模式发生器控制难以做出快速的调整反应。因此，有效的中枢模式发生器柔顺行走控制策略应该从模型的主动调整出发，通过控制四足机器人各关节的关节角度、关节角的运动速度和相位关系使机器人产生柔顺运动方式，从而减小碰撞力突变带来的身体姿态剧烈变化。

从主动调整模型的角度出发，设计柔顺行走控制策略如下：

（1）调整落地与抬起阶段髋关节俯仰自由度的步幅，通过增大碰撞阶段髋关节的摆动幅度形成机器人本体相对于地面的缓冲；

（2）针对 （1）中步幅变化引起的关节轨迹不连续现象，设计步幅递变函数；

（3）增加幅值调整阶段的运动周期，减小落地与抬起阶段的关节角变化速度。

2.2 中枢模式发生器柔顺行走控制模型

在基于Hopf振荡器的中枢模式发生器中，输出的髋关节信号和膝关节信号幅值变化一致，由同一变量μ 控制，当需要调节髋关节幅值时会同时引起膝关节幅值的改变，导致关节之间运动相位关系紊乱。为此，设计2个Hopf振荡器组成相互作用的一个神经元同时控制四足机器人一条腿的运动，2 个振荡器分别被标记为a 和b，具有相同的振荡频率，振荡器a 提供膝关节运动信号，振荡器b提供髋关节运动信号，同时，将振荡器a的髋关节运动信号作为基准信号，用于调整振荡器b的髋关节信号。基于Hopf振荡器的中枢模式发生器改进模型如下

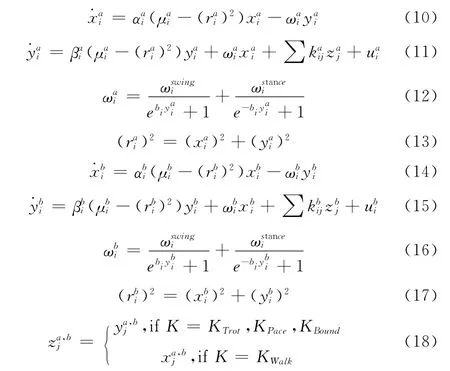
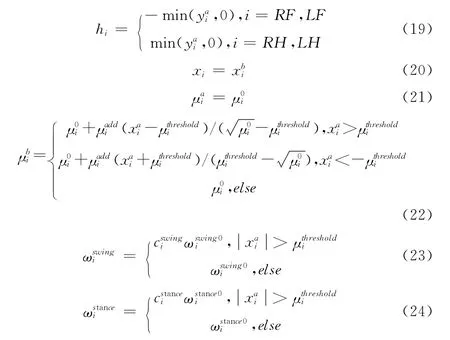
上述柔顺行走控制模型的参数描述见表1。在四足机器人运动的幅值基数和频率基数基础上，利用变换函数灵活调整各腿的运动步幅和频率，实现柔顺行走控制。

表1 中枢模式发生器柔顺行走控制模型参数说明

2.3 节律运动柔顺性评估方法

四足机器人柔顺行走研究目前处于起步阶段，相关研究内容较少，尚没有涉及针对柔顺性评估方法的研究。本文根据四足机器人运动不连续问题提出相应的柔顺性评价指标，并以此为柔顺行走控制研究提供必要的理论评价依据。首先，四足机器人从摆动相向站立相切换时产生的较大突变碰撞力是引起柔顺性低的主要原因，因此，在中速及慢速步态下，忽略由机器人运动加速度产生的作用力因素，考虑碰撞力与机器人自身重力之间的关系，构建如下所示的碰撞力评价函数

式中：Fv——触地时刻的垂直方向碰撞力，m——机器人整体质量，g——重力加速度，Ni——触地时处于站立相的腿的数目，当处于Trot、Pace或Bound步态时，Ni＝2，当处于Walk步态时，Ni＝3，CF描述碰撞力与重力之间的比例关系。其次，从运动姿态方面对柔顺性进行评估。因四足机器人运动的平稳性直接反映到自身的状态变化，本文从质心在垂直方向上的变化趋势以及加速度情况分析四足机器人的柔顺性强弱。仿真过程采用的均为离散数值求解，第k个质心点处的加速度ak可表示为

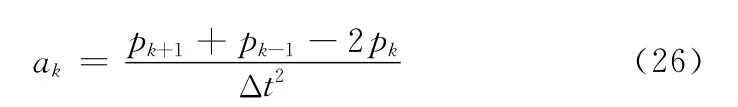
式中：pk——第k个质心点的位置，Δt——采样时间间隔。姿态评价函数建立如下

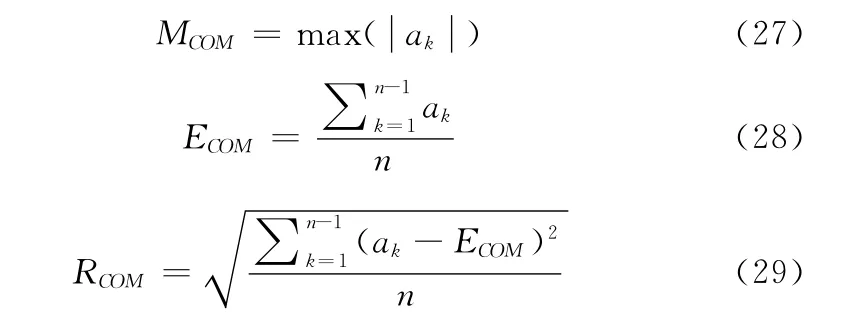
式中：n——质心点数目，MCOM——质心加速度最大绝对值，ECOM——质心加速度均值，RCOM——质心加速度均方差，反映各时刻加速度之间的相对变化情况。

3 柔顺行走控制仿真实验

根据本文所设置的动力学环境条件，对未经改进的中枢模式发生器控制方法和所提出的柔顺行走控制方法进行仿真对比实验。仿真开始阶段采用未经改进的中枢模式发生器控制，经过过渡调节，转换到柔顺行走控制。

3.1 Trot步态柔顺行走控制仿真实验

对角小跑步态柔顺行走控制仿真中，对于每条腿所在的振荡器a、b，设置振荡器的幅值基数μ0＝1，幅值调整变量μadd＝3，幅值调整阈值μthreshold＝0.7，腿的基频率ωstance0＝ωswing0＝2＊π，频率调整变量cstance＝cswing＝0.5，频率调整参数b＝100，收敛速度变量α＝β＝50，上层输入或反馈变量u＝0。

对角小跑步态关节运动轨迹如图6所示，原节律运动步幅为10°，周期为1s，经过一个运动周期的过渡，转换成柔顺行走控制运动，落地阶段与抬起阶段的步幅调整为20°，整个步态周期变为1.65s。从轨迹图可以看出，过渡过程稳定，且柔顺行走控制步态周期中的幅值和频率变化连续。足端碰撞力如图7所示，在3.5s之后进入柔顺行走控制阶段，足端突变碰撞力大幅减小，维持在1500Newton左右。图8显示了对角小跑步态下垂直方向质心轨迹及质心加速度轨迹，可以看出，柔顺行走控制下质心运动范围增加，轨迹柔顺性增强，质心加速度范围缩小，最大加速度从86254mm／s2降至23052 mm／s2，反映出四足机器人在对角小跑步态下整体运动姿态的连续性增强。

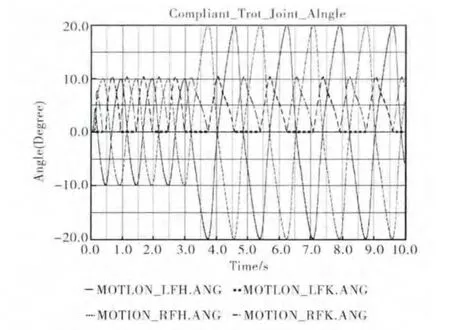
图6 Trot步态柔顺行走控制关节运动轨迹

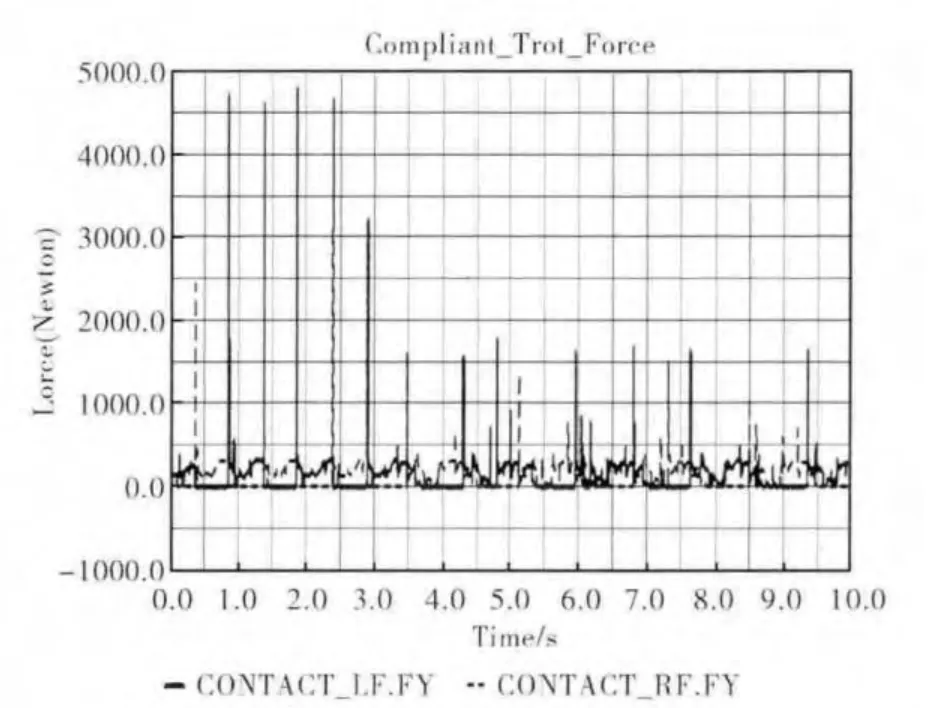
图7 Trot步态柔顺行走控制碰撞力

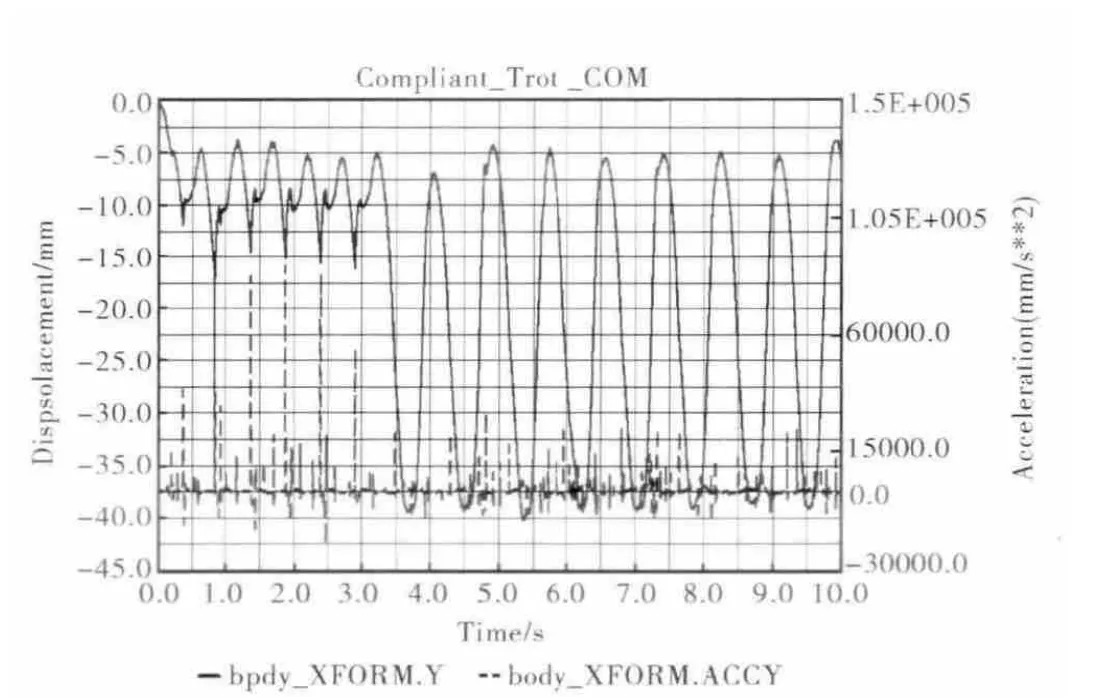
图8 Trot步态柔顺行走控制质心轨迹与质心加速度轨迹

根据所提出的柔顺性评估指标，在对角小跑步态下采样原节律运动和柔顺行走控制运动的10个运动周期，并取其均值进行比较，比较结果见表2。四足机器人仿真模型的总质量为50kg，重量为490Newton，碰撞力评价指标从18.8070降低到5.5177，为原来的29.34%；质心峰值、均值以及均方差相比原节律运动控制均有较大幅度的下降。从以上分析可知，所提出的柔顺行走控制方法使四足机器人对角小跑步态的柔顺性提高，具有较好的控制效果。

表2 Trot步态柔顺性评估指标对比

3.2 Walk步态柔顺行走控制仿真实验

慢走步态柔顺行走控制仿真实验中，对于每条腿所在的振荡器a、b，振荡器基频率设置为ωstance0＝4＊π，ωswing0＝π，其余参数与对角小跑步态仿真实验相同。慢走步态下的关节运动轨迹如图9所示，图中上半部分显示的是左腿节轨迹，下半部分显示的是右腿关节轨迹，原节律运动步幅为10°，周期为1.25s，在5.7s时进行切换，转换成柔顺行走控制运动，步幅调整为20°，整个步态周期变为2.35s。从轨迹图可以看出，在柔顺行走控制慢走步态下关节运动轨迹平滑连续。足端碰撞力如图10所示，与原节律控制相比，柔顺行走控制阶段足端突变碰撞力减小，维持在2000Newton左右。图11显示的是慢走步态下垂直方向质心轨迹及质心加速度轨迹，可以看出，柔顺行走控制下质心运动范围增加，质心加速度范围缩小，连续性增强，反映出四足机器人在慢走步态下姿态柔顺性的提高。值得注意的是柔顺行走控制时的质心轨迹存在一定的跳变，这是由于中枢模式发生器控制无法有效调整四足机器人的运动稳定性引起的。

根据所提出的柔顺性评估指标，在慢走步态下采样原节律运动和柔顺行走控制运动的10个周期，并取其均值进行比较，比较结果见表3。碰撞力评价指标从25.8098降低到9.8168，为原来的38.02%；质心峰值、均值以及均方差相比原节律运动控制均有较大幅度的下降，指标整体变化趋势与对角小跑步态下一致。从以上分析可知，所提出的柔顺行走控制方法在慢走步态下柔顺性提高，控制效果显著提升。

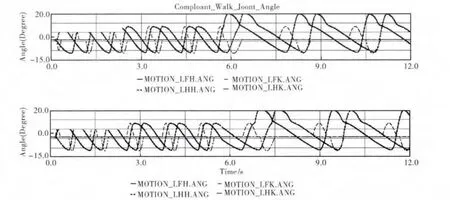
图9 Walk步态柔顺行走控制关节运动轨迹

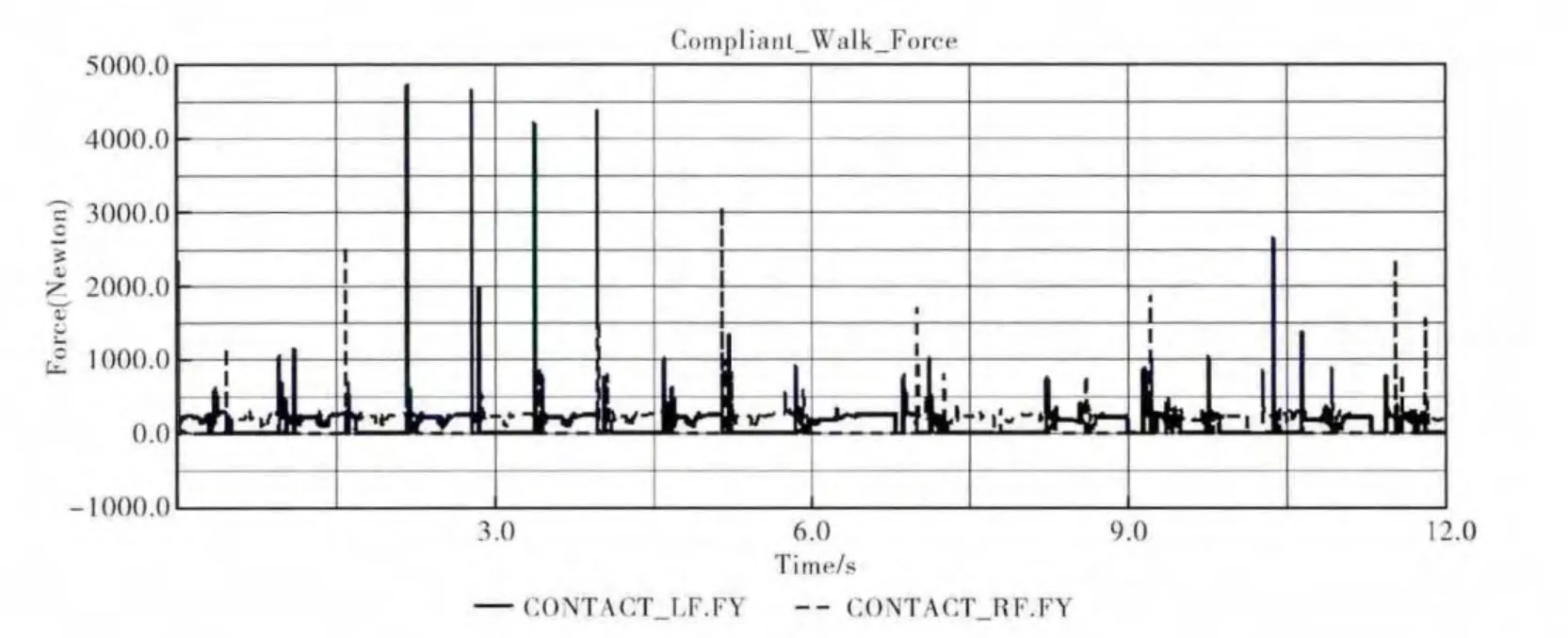
图10 Walk步态柔顺行走控制碰撞力

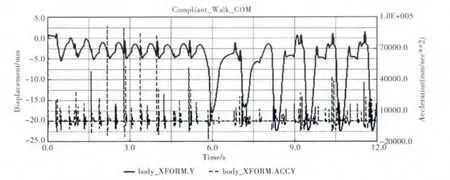
图11 Walk步态柔顺行走控制质心轨迹与质心加速度轨迹

表3 Walk步态柔顺性评估指标对比

4 结束语

本文在基于Hopf振荡器的中枢模式发生器基础上进行四足机器人柔顺行走控制研究，一方面研究中枢模式发生器的信号整合、步态生成，另一方面针对足机器人运动不连续、足端与地面之间存在较大突变碰撞力的问题，探索柔顺行走控制策略，并提出柔顺性评价指标进行仿真实验验证。

通过分析Hopf振荡器的信号输出特点，将振荡器的输出信号x、y整合到同一条腿的髋关节和膝关节控制中，简化了控制模型。此外，对称步态下中枢模式发生器的拓扑结构耦合作用强，相位关系锁定，难以产生慢走步态，对此，本文改变了模型的耦合作用关系，构建了慢走步态下的拓扑结构，能够产生稳定的慢走步态控制信号。

针对四足机器人节律行走过程中突变碰撞力大、运动柔顺性低的问题，将瞬时碰撞力和质心轨迹引入评价系统，建立碰撞力与机器人本体重力的关系函数，将质心加速度的峰值、均值与均方差作为评价身体姿态变化的指标；根据动物生物力学的特点，改变落地和抬腿阶段的步幅，在碰撞阶段形成机器人本体与地面之间的缓冲，设计幅值递变函数防止轨迹不连续现象的发生，同时增大轨迹调整阶段的周期，减小触地时关节角的运动速度。最后，基于改进的柔顺行走控制模型进行对角小跑和慢走仿真实验，柔顺性均取得较大改善。

［1］Zhang Xiuli，Zheng Haojun.Autonomously clearing obstacles using the biological flexor reflex in a quadrupedal robot ［J］.Robotica，2008，26 （1）：1－7.

［2］Zhang Xiuli，Zheng Haojun.Walking up and down hill with a biologically inspired postural reflex in a quadrupedal robot［J］.Autonomous Robots，2008，25 （1）：15－24.

［3］LI Bin，LI Yibin，RUAN Jiuhong，et al.Study of quadruped robot gait planning based on Wilson－Cowan neural oscillators［J］.Journal of Shandong University Engineering Science，2010，40 （1）：6－9 （in Chinese）. ［李彬，李贻斌，阮久宏，等.基于Wilson－Cowan神经振荡器的四足机器人步态规划研究 ［J］.山东大学学报，2010，40 （1）：6－9.］

［4］Fitzhugh R.Impulses and physiological states in theoretical models of nerve membrane［J］.Biophysical Journal，1961，1（6）：445－466.

［5］Nagumo J，Arimoto S，Yoshizawa S.An active pulse transmission line simulating nerve axon ［J］.Proceedings of the IRE，1962，50 （10）：2061－2070.

［6］Matsuoka K.Sustained oscillations generated by mutually inhibiting neurons with adaptation ［J］.Biological Cybernetics，1985，52 （6）：367－376.

［7］LI Bin.The algorithm and implementation of gait control and gait transition for quadruped robots ［D］.Beijing：Chinese Academy of Sciences，2011 （in Chinese）.［李斌.四足机器人步态控制与步态变换的算法及其实现 ［D］.北京：中国科学院自动化研究所，2011.］

［8］Ijspeert A J.Central pattern generators for locomotion control in animals and robots：A review ［J］.Neural Networks，2008，21 （4）：642－653.

［9］Righetti L，Ijspeert A J.Pattern generators with sensory feedback for the control of quadruped locomotion ［C］／／IEEE International Conference on Robotics and Automation，2008：819－824.

［10］Kimura H，Fukuoka Y，Cohen A H.Adaptive dynamic walking of a quadruped robot on natural ground based on biological concepts ［J］.The International Journal of Robotics Research，2007，26 （5）：475－490.