海上大位移井固井顶替数值模拟研究

李 昊，王金堂，孙宝江，曹成章，李春莉，徐渴望

[1. 中国石油大学(华东)石油工程学院，山东 青岛 266580；2. 中石化胜利石油工程有限公司钻井工艺研究院，山东 东营 257017；3. 中国石化胜利油田有限公司胜利采油厂地质研究所，山东 东营 257015]

海上大位移井固井顶替数值模拟研究

李 昊1，王金堂1，孙宝江1，曹成章2，李春莉3，徐渴望1

[1. 中国石油大学(华东)石油工程学院，山东 青岛 266580；2. 中石化胜利石油工程有限公司钻井工艺研究院，山东 东营 257017；3. 中国石化胜利油田有限公司胜利采油厂地质研究所，山东 东营 257015]

顶替效率及界面稳定性是海上大位移井固井顶替能否成功的关键因素。应用计算流体力学理论，结合南海一口大位移井固井基础资料，通过数值模拟得到了水泥浆流变性以及不同井眼情况对固井顶替效率的影响规律。计算结果表明：增大水泥浆稠度系数，顶替效率增加；增大水泥浆流性系数，顶替效率减小；固井顶替效率随着屈服应力增加先增大后降低，最终趋于稳定；固井时水泥浆的流性指数不宜过高，n值应控制在0.6以内；稠度系数应大于1.5 Pa·sn，不应超过3 Pa·sn；屈服应力在10～18 Pa的范围区间，有利于水泥浆顶替钻井液。偏心度对界面稳定性影响很大，建议将偏心度控制在0.5以内；使用套管扶正器，界面的稳定性明显改善，优选出最佳刚性扶正器旋流角为60°；套管屈曲对界面稳定性的影响显著，使环空界面的顶替效率明显降低。

大位移井； 环空结构； 顶替效率； 界面稳定性； 数值模拟

0 引 言

大位移井钻完井技术的发展为高效开发海上油气田提供了有效途径[1-3]。大位移井一般定义为水平位移与垂身之比大于或等于2且测深大于3 000 m的井或水平位移超过3 000 m的井[4]。大位移井固井顶替主要面临如下技术难题[5-8]：一是水平井段很长，钻井液驱替难度大；二是在大斜度井眼及水平段的条件下，套管总是贴近井壁向下一侧，受摩擦力影响，上提、下放阻力大，容易造成套管屈曲变形，产生不规则的井眼环空；三是套管自重造成套管柱偏心，影响固井顶替效率及界面稳定性。井眼状况参数、钻完井液流变参数、固井施工参数等是提高海上大位移井固井顶替效率的关键技术指标。

非牛顿赫巴流体在偏心环空中的流动方程表示复杂，理论求解比较困难。本文应用计算流体力学软件FLUENT，结合南海一口实际大位移井，数值模拟了大位移井固井顶替过程，分析了水泥浆流变性和环空流道结构对大位移井固井顶替的影响规律，从而找出提高顶替效率的方法和优化方案，为海上大位移井固井提供理论设计指导。

1 环空流道几何模型及网格划分

1.1 几何模型

环空流道几何模型采用三维空间模型，计算区域为长度10 m、外径为0.215 9 m、内径0.139 7 m的环空流道。可以根据计算需要，改变井斜角、无量纲偏心度，模拟不同类型套管扶正器和不同套管屈曲类型的环空流道。

1.2 网格划分

在数值模拟计算中，网格的划分是一个极其重要的问题，高质量的网格是成功实现数值模拟的首要条件，网格过疏或者过密都会对计算结果产生直接的影响。网格过疏会导致计算结果不精确，在一定情况下甚至会造成计算结果不收敛；而网格过密不仅会使计算量大幅增加，而且对计算机的硬件要求也较高。在满足网格密度的条件下，应当尽量减少计算量，提高计算收敛的稳定性和收敛速度。图1所示为45°螺旋刚性扶正器环空流道整体网格划分，在螺旋流道周围进行了局部加密，其网格数为3.5×105。

图1 45°螺旋刚性扶正器环空流道网格划分Fig.1 Annulus flow channel geometric model and its meshing of whirl rigid centralizer with the helix angle of 45°

2 大位移井环空固井顶替理论模型

2.1 基本控制方程

针对井眼环空流道结构(模型如图2所示)，建立了流动控制方程,包括质量守恒方程和动量守恒方程。考虑实际顶替条件，模拟计算时使用标准的k-ε两方程模型[9-10]。

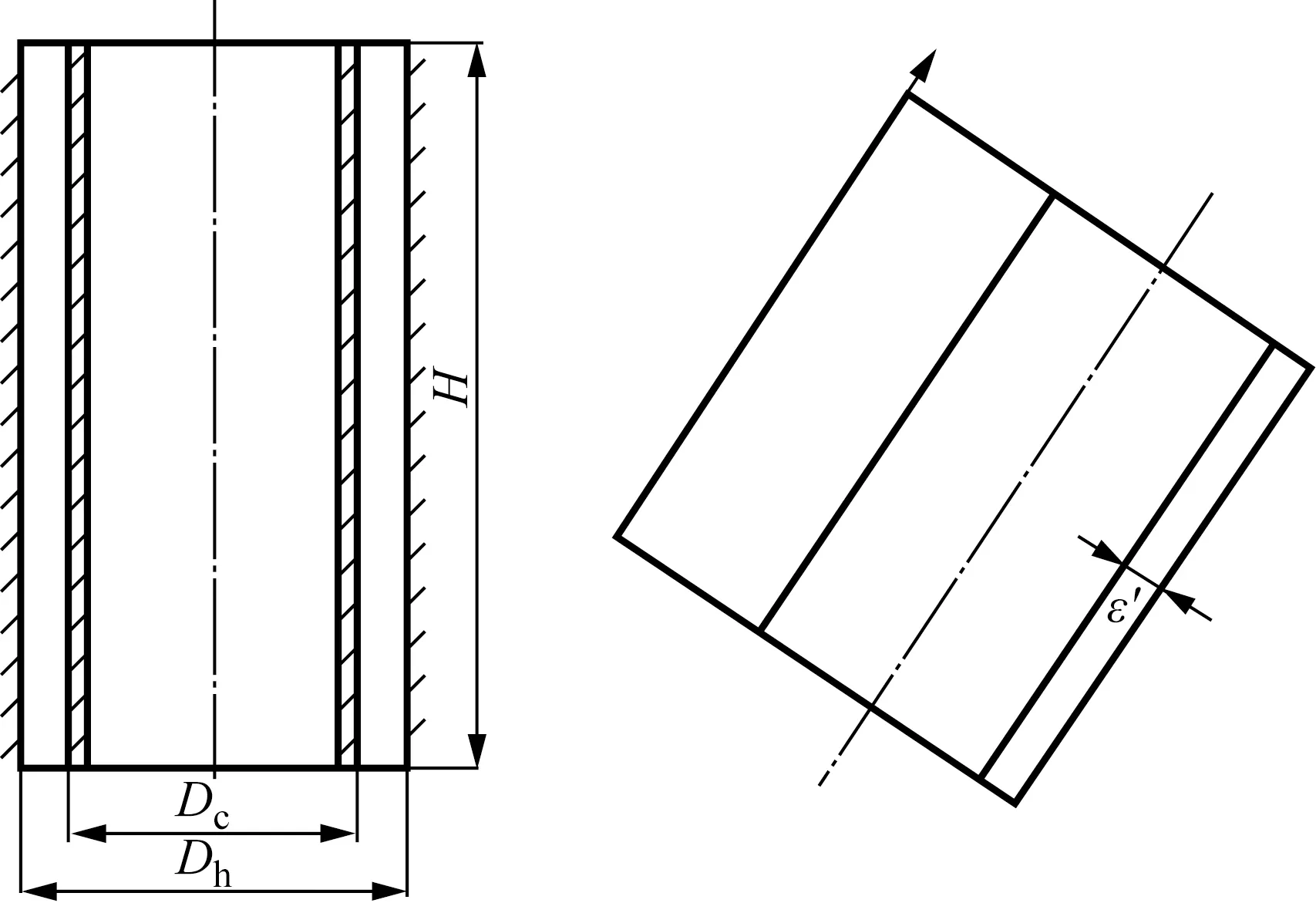
图2 井眼环空流动分析示意图Fig.2 Schematic diagram of borehole annulus flow analysis

质量守恒方程为

(1)

动量守恒方程为

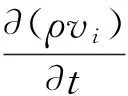
(2)

湍流输运方程为

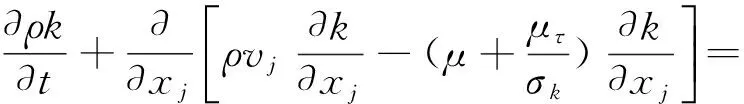
(3)

能量耗散输运方程为

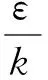
(4)

对于两相流有

ρ=α1ρ1+α2ρ2.

(5)

式(1)～(5)中：ρ为流体密度，kg/m3；α1、α2分别为两相的质量分数；ρ1、ρ2分别为两相的密度，kg/m3；t为时间项，s；v为速度项，m/s；F为单位质量上的质量力；p为压力项，Pa；μτ为涡粘性；Sij为平均速度张量；k为湍动能；ε为湍流耗散率；f为衰减函数；τtij为雷诺应力项；φk、φε为壁面项。

以上方程组具有强烈非线性，理论求解困难，本文采用数值求解。数值方程离散时，在空间上采用非结构化的六面体网格，应用的数值离散方法是双精度有限体积方法，对流项采用一阶迎风格式，压力速度场的耦合求解利用改良后的SIMPLEC方法。

2.2 辅助方程及边界条件

辅助方程包括赫巴流体本构方程、偏心度模型等[11]。

赫巴流体本构方程写作

(6)

偏心度模型中，定义无量纲偏心度e为

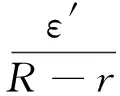
(7)

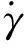
边界条件及流体性质如下：入口采用速度入口边界条件，注入速度为1.5 m/s，流动为湍流；出口为压力边界；固壁采用无滑移边界条件，壁面上u=0，壁面附近采用壁函数法。

理论研究表明，非牛顿赫巴流体能够充分反映水泥浆高温高压下的流变性能[12]。本文配置三种不同配方的海水水泥浆体系，通过实验测试了不同温度条件下的流变性能，结果均表现为赫巴流体模式。结合南海一口大位移井固井基础资料，固井液体系采用赫巴流体进行模拟，密度、稠度系数、流性指数和屈服值如表1所示。

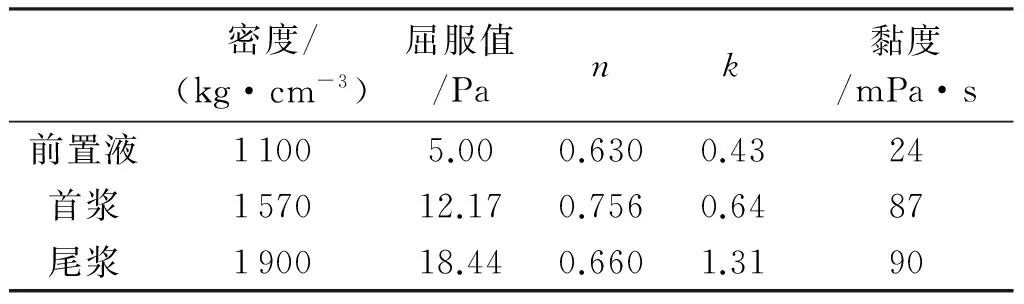
表1 南海某大位移井固井液体系流变性

3 模拟结果分析

3.1 水泥浆流变性模拟结果分析

3.1.1 水泥浆稠度系数对顶替效率的影响

水泥浆稠度系数K与水泥浆的黏度、切力联系在一起，与流体在剪切速率为1 s-1时的黏度有关[13]。改变水泥浆的稠度系数分别为0.2、0.6、1.0、1.2、1.5、3.0、5.0 Pa·sn，其余参数条件不变，得到不同水泥浆稠度系数K下的顶替效率关系曲线，如图3所示。

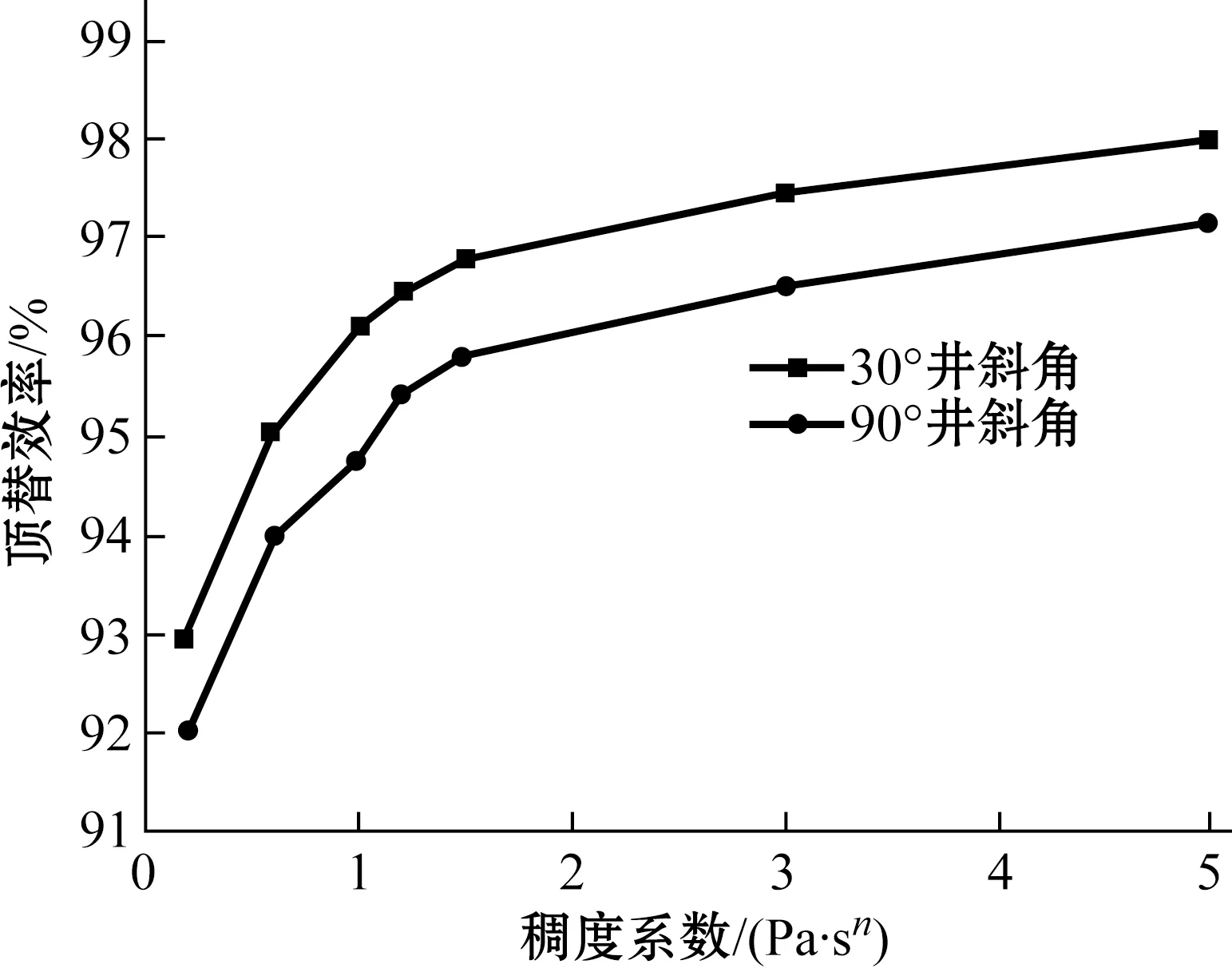
图3 水泥浆的稠度系数对顶替效率的影响Fig.3 Effect of consistency coefficient on displacement efficiency under different deviation angles

从图3可以看出，当水泥浆的稠度系数在0.2～1.5 Pa·sn之间时，顶替效率随着稠度系数的增加而增大；而稠度系数在1.5～5 Pa·sn之间时，顶替效率随稠度系数增加而基本保持不变。因此，固井时稠度系数应大于1.5 Pa·sn，不应超过3 Pa·sn。满足这些要求有利于降低环空流动的不均匀性，对替净环空钻井液非常有利。

3.1.2 水泥浆流性指数对顶替效率的影响

在赫巴模式中，流性指数n表示假塑性流体在一定剪切速率范围内所表现出的非牛顿性的程度[13]。改变水泥浆的流性指数分别为0.2、0.3、0.4、0.5、0.6、0.7、0.8，其余参数条件不变，得到不同水泥浆流性指数下的顶替效率关系曲线，如图4所示。

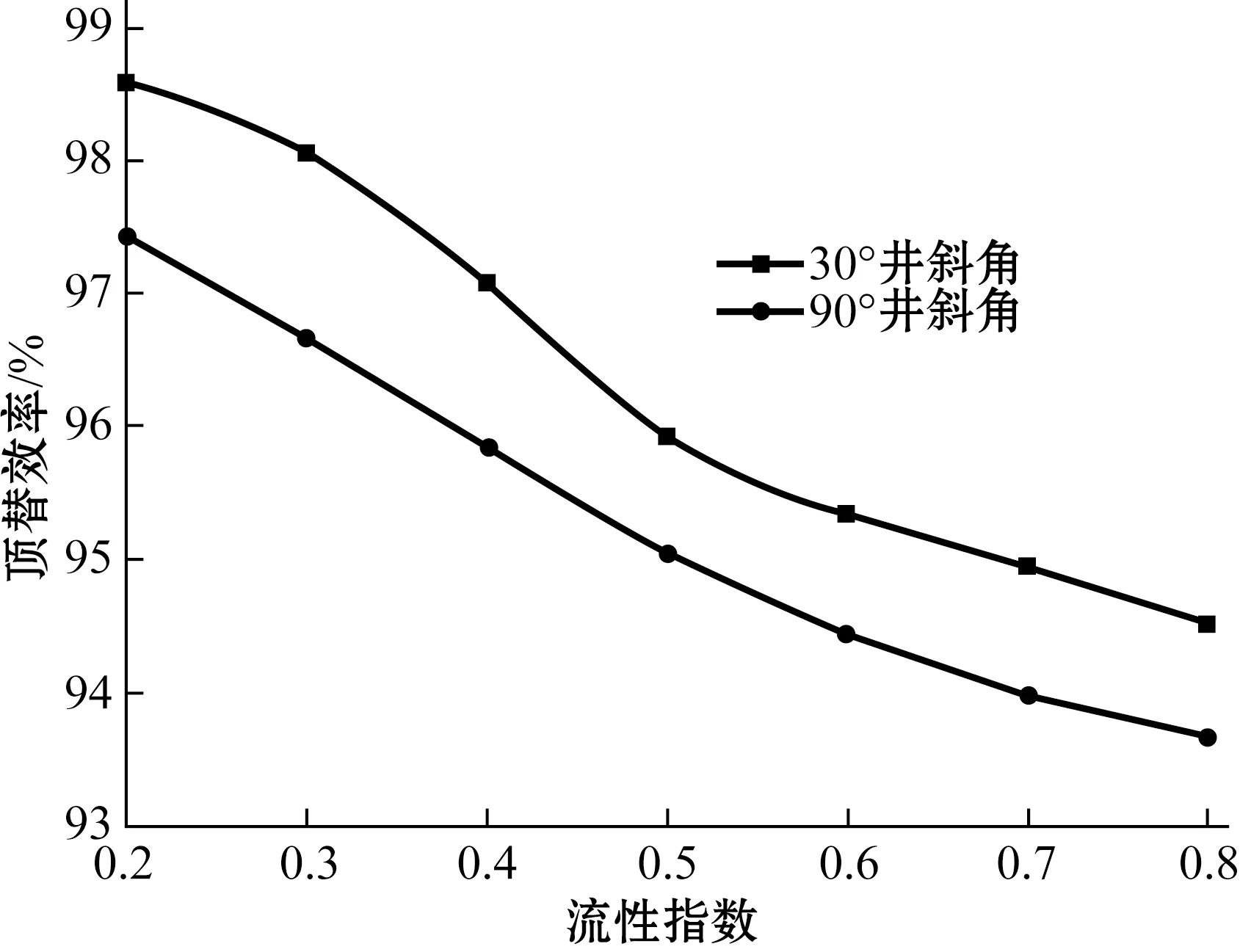
图4 不同井斜角水泥浆的流性指数对顶替效率的影响Fig.4 Effect of flow index on displacement efficiency under different deviation angles

从图4可以看出，增大水泥浆流性指数，顶替效率减小。随着流性指数n值的增大，环空速度剖面逐渐变得尖锐，宽、窄间隙的流速差增加，流动的不均匀度增加，从而导致流动不稳定性的增加。因此，进行固井时水泥浆的流性指数不宜过高，n值应控制在0.6以内。

3.1.3 水泥浆屈服应力对顶替效率的影响

屈服应力能反映水泥浆在管中再启动的难易程度，是衡量水泥浆流动性的重要指标之一。改变水泥浆的屈服应力分别为5、10、18、26、40 Pa，其余参数条件不变，同样得到不同水泥浆屈服应力下的顶替效率关系曲线，如图5所示。

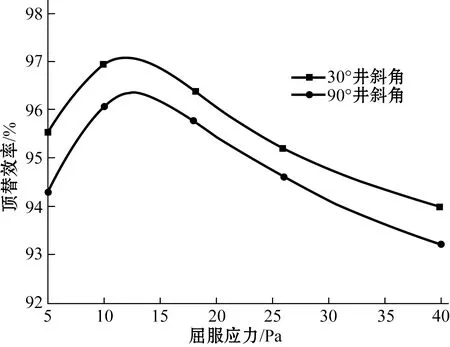
图5 水泥浆的屈服应力对顶替效率的影响Fig.5 Effect of yield stress on displacement efficiency under different deviation angles

从图5可以看出，当水泥浆的屈服应力在5～10 Pa之间时，顶替效率随着屈服应力的增加而增大；当水泥浆的屈服应力在10～40 Pa之间时，顶替效率随屈服应力增加而逐渐下降。因此，10～18 Pa的屈服应力范围区间有利于水泥浆顶替钻井液。

3.2 环空流道结构对大位移井固井顶替影响分析

3.2.1 偏心度对固井顶替效率的影响

设置环空无量纲偏心度为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8，井斜角包含0°、30°、60°、90°几种情形，分别在顶替流速为1.5 m/s的条件下进行模拟。

图6为井斜角为90°、偏心度e=0.5时，水泥浆固井顶替界面分布云图，图中红色区域为水泥浆(1)，蓝色区域为钻井液(0)。模拟结果得出，在相同的顶替速率下，偏心度对界面稳定性影响很大。在0°～60°井斜角条件下，偏心度为0～0.2时，界面比较稳定，只是在速度较高时略有波动，此时固井质量容易保证。随着偏心度的增加，顶替界面将产生倾斜；在偏心度为0.5时，界面倾斜度明显高于偏心度为0.2时，同时产生了明显的尾迹，界面发生失稳，顶替效率不能得到保证；当偏心度达到0.8时，顶替界面泥浆的尾迹更加明显，顶替界面严重失稳，无法实现正常顶替，顶替效率明显降低。

图6 井斜角为90°、偏心度e=0.5时，水泥浆固井顶替界面分布云图Fig.6 Distribution of displacement interface changing with time when the eccentricity is 0.5 and the well deviation angle is 90°

图7为不同井斜角条件下不同偏心度顶替效率曲线图。在0°、30°、60°、90°井斜角情况下，顶替效率随着偏心度的增加而降低，特别是在偏心度大于0.5以后，顶替效率下降趋势非常明显；当井斜角增大到90°时，顶替效率随着套管偏心度增大而减小的趋势趋于平缓，即在大位移井水平段，套管具有一定程度的偏心时顶替界面在环空内保持稳态，对顶替效率影响不大。

偏心引起界面失稳是轴向、径向速度分布不均造成的。由于偏心的存在，使得宽、窄间隙处的阻力不同，从而产生轴向速度的差异。偏心度越大，速度差异越明显，界面就越不稳定，顶替效率也越差。这一点已有许多学者从理论及实验方面给予了证明[14-15]。降低套管的偏心度是保证顶替界面稳定、提高顶替效率的有效手段。在一般井斜角固井段，为保证固井质量有较高的顶替效率，建议将偏心度控制在0.5以内。

在控制套管偏心度方面，首先应从抓好钻井质量入手，尽量减小井斜；其次，在井况不好的情况下，应采用新的顶替工艺，如旋转套管固井工艺，可取得好的效果。另外，也可以采用旋流套管扶正器，不仅可提高套管居中度，而且能使环空液体由直流变为旋流，减少水泥浆窜槽。

3.2.2 不同流道类型扶正器对顶替效率的影响

(1) 不同流道类型扶正器数值模拟。现场使用的扶正器一般有单弓扶正器、双弓扶正器和刚性旋流扶正器。添加扶正器可以使套管居中，减少偏心，提高顶替效率。根据现场实际，建模所用的扶正器的尺寸包含这三种类型，其中刚性扶正器根据套扶扶条与轴向方向的角度分为0°螺旋角、30°螺旋角、45°螺旋角和60°螺旋角刚性旋流扶正器。考虑大位移井特点，井斜角分别为30°和90°。

从图8可以看出，单弓扶正器和双弓扶正器对改善顶替界面稳定效果不大，只是有较好的扶正作用。当井斜角增大到一定程度时，扶正器扶条的强度有限，套管下行重力的挤压作用会使扶正器失效，扶正套管的效果不明显。在大位移井水平段不建议采用单弓扶正器和双弓扶正器，应当选用刚性较好的旋流扶正器。螺旋形结构的扶正条的存在改变了环空的流道结构，使流体不但产生轴向速度，还增加了周向速度，对井眼一些虚滤饼的冲刷和顶替效果很好。

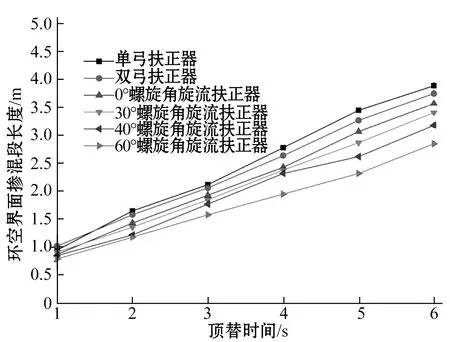
图8 90°井斜角不同套管扶正器类型条件下顶替界面长度随顶替时间变化规律Fig.8 Variation of displacement interface length with displacement time when using different kinds of casing centralizers

旋流扶正器通过在圆柱衬套上呈螺旋形分布的扶正条形成螺旋流道，能产生环向流速场。所建的30°螺旋角旋流扶正器模型为扶正条与井眼轴线方向呈30°夹角螺旋上升，通过数值模拟得到水泥浆固井顶替界面分布及扶正器处环空流道流场，如图9、图10所示。

图9 30°井斜角30°螺旋角旋流扶正器顶替界面分布云图Fig.9 Distribution of displacement interface changing with time when the helix angle of rigid centralizer is 30° and the well deviation angle is 30°

图10 30°井斜角30°螺旋角旋流扶正器位置出口处截面速度分布云图Fig.10 Velocity distribution at the section of exit position of whirl rigid centralizer when the helix angle is 30° and the well deviation angle is 30°

从模拟结果中可以看出，由于螺旋形结构的扶正条的存在，改变了环空的流道结构，使流体不但产生轴向速度，还增加了周向速度分量，对井眼一些虚滤饼的冲刷和顶替效果很好。从扶正器位置出口处截面速度分布云图中也可以看出，在出口处速度的变化比较明显，速度最大处可以达到2.48 m/s，有利于水泥浆顶替紊流程度的增加。因此，旋流扶正器可以加大流体的携带能力并提高水泥浆顶替效率。

(2) 最佳刚性扶正器旋流角的优选。固井注水泥浆时，由于流体流经旋流扶正器时受到扶正器扶正条的限制和导向作用，必然使流出扶正条的水泥浆流动的迹线发生改变，在环空形成螺旋状流速场。这种流速场进入环空后，受到环空已存在流体的淹没阻尼作用，因此在流动过程中逐渐衰减，流体在环空生成的旋流范围是有限的。现场施工表明，下入旋流扶正器对正常的固井施工作业不会产生不良影响。下入扶正器后，在有效的旋流段内改变了顶替流动方式，保证了顶替效率。不同旋流角对水泥浆的旋流效果不同。根据所模拟的0°、30°、45°、60°旋流扶正器的模拟结果，优选出最佳刚性扶正器旋流角。

图11为不同旋流角扶正器顶替效率曲线。当扶正条螺旋角在一定范围内(30°～60°)增大时，旋流长度随之增大，固井顶替效率也会随之升高。当扶正条螺旋角在较小的范围内(30°～45°)增大时，旋流长度增大得较快，但当扶正条螺旋角较大(50°以上)时，扶正条旋流角度再增大，固井顶替效率增加得很少，趋于稳定值。总之，套管旋流扶正器对固井顶替效率的提高有一定的促进作用，结合海上油田固井现场实际工况和数值模拟结果，推荐使用60°螺旋角旋流扶正器来使套管居中。

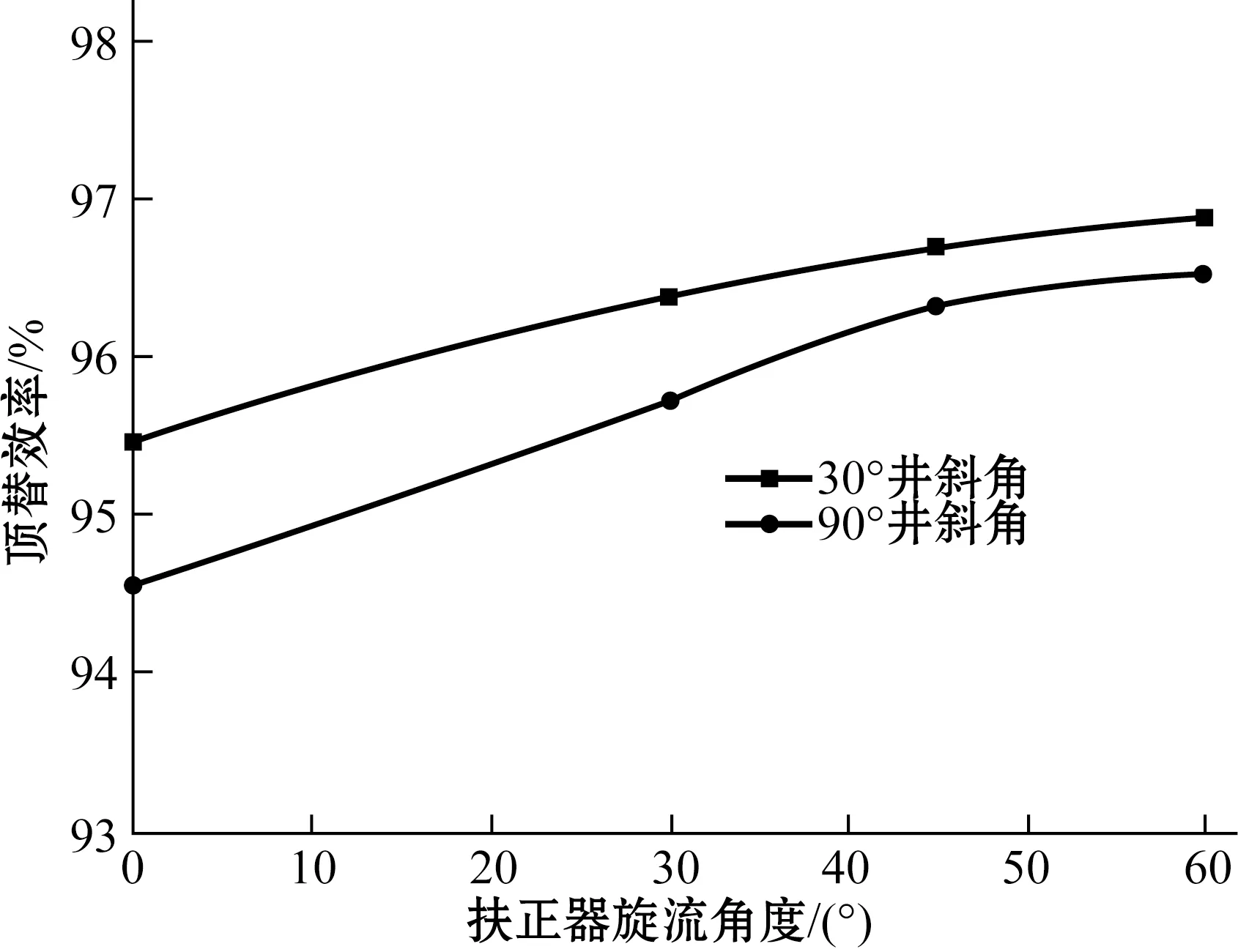
图11 不同旋流角扶正器顶替效率Fig.11 Displacement efficiency using centralizers with different helix angles

3.2.3 套管屈曲对大位移井固井顶替的影响

在实际的大位移井水平段下套管过程中，套管可能沿某些弱点首先发生破坏，产生不稳定的屈曲变形。随着外加轴向载荷的增大，套管沿着井眼低边形成蛇形状态的正弦屈曲；如果载荷继续增大，套管将不再是蛇形，而是弯曲地环绕井壁成螺旋式屈曲，套管压缩像弹簧，充满整个井眼[16]。套管串屈曲时受到井眼约束，形成偏心度不断变化的井眼环空，在套管贴近井壁处会有残余钻井液不能完全顶替，对固井质量产生很大影响。本文所建立的物理模型包括正弦屈曲和螺旋屈曲，套管摆动最大幅值0.038 1 m，通过模拟顶替界面分布和顶替效率，评价套管屈曲对大位移井固井质量的影响。图12、图13为套管正弦屈曲和螺旋屈曲环空流道水平段顶替界面分布。

图12 套管正弦屈曲环空流道水平段顶替界面分布Fig.12 Distribution of displacement interface at the horizontal section of annulus flow channel under the condition of casing sinusoidal buckling

图13 套管螺旋屈曲环空流道水平段顶替界面分布Fig.13 Distribution of displacement interface at the horizontal section of annulus flow channel under the condition of casing helical buckling

从界面分布图中看出，在环空流道类型和重力的共同作用下，不论是套管正弦屈曲环空还是套管螺旋屈曲环空界面的掺混区域变长，水泥浆均分布在环空下部，在套管与井壁接触的部位水泥浆不能充分顶替，水泥浆靠近壁面处出现较长的尾迹且有间断。数值模拟计算得出套管产生正弦屈曲时，顶替效率为90.16%；而在套管发生螺旋屈曲的情况下，其顶替效率只有89.62%。在此情形下，对于大位移井固井来说，整体的顶替效率不能得到保证，严重影响固井质量。

在大位移井水平段套管下入过程中，一定要保证套管的刚度和强度，避免产生套管串的屈曲变形。同时，为了减小下套管的阻力，建议采用漂浮下套管技术，或者使用滚轴刚性扶正器，既可减小发生套管屈曲的几率又能保证套管居中，改善井眼环空结构，提高顶替界面稳定性和固井顶替效率，保证固井质量。

4 结 论

根据南海一口大位移井固井的基础资料，结合FLUENT软件，对大位移井水泥浆顶替过程进行了数值模拟研究，得到了水泥浆流变性和环空流道结构对大位移井固井顶替的影响规律：

(1) 增大水泥浆稠度系数，顶替效率增加；增大水泥浆流性系数，顶替效率减小；顶替效率随着屈服应力的增加先增加后降低。固井时水泥浆的流性指数不宜过高，n值应控制在0.6以内；稠度系数应大于1.5 Pa·sn，不应超过3 Pa·sn；屈服应力在10～18 Pa的范围内时，有利于水泥浆顶替钻井液。

(2) 偏心度越大，速度差异越明显，界面越不稳定，顶替效率也越差。为保证固井质量有较高的顶替效率，建议将偏心度控制在0.5以内。

(3) 单弓扶正器和双弓扶正器对改善顶替界面稳定效果不大，只是有较好的扶正作用；旋流扶正器可以加大流体的携带能力并提高水泥浆顶替效率。经模拟，优选出了适合于大位移井的60°螺旋角旋流扶正器来使套管居中。

(4) 套管屈曲对界面稳定性的影响显著，使得环空界面的掺混区域变长，导致整体的顶替效率不能得到保证。

[1] Modi S, Mason C J, Tooms PJ, et al. Meeting the 10 km drilling challenge [C]. SPE, 1997: 38583.

[2] 吴爽，李骥，张焱. 大位移井技术研究的现状分析[J]. 石油钻探技术， 2002， 30(5)： 17.

[3] Dutra ES, Martins AL, Miranda C R, et al. Dynamics of fluid substitution while drilling and completing long horizontal-section wells [C]. SPE, 2005: 94623.

[4] 蒋世全. 大位移井技术的发展现状及启示[J]. 中国海上油气(工程)， 1999， 11(3)： 14.

[5] 连吉弘，康建平. 大位移井固井技术分析[J]. 长江大学学报：自然科学版, 2010， 7(1)： 205.

[6] 陈家琅，黄匡道，刘永健，等. 定向井固井注水泥顶替效率研究[J].石油学报， 1990， 11(3)： 98.

[7] 王瑞和，李明忠，王成文，等. 油气井注水泥顶替机理研究进展[J]. 天然气工业， 2013， 33(5)： 69.

[8] Couturler M, Guillot D, Hendriks H, et al. Design rules and associated spacer properties for optimal mud removal in eccentric annuli [C]. CIM/SPE International Technical Meeting, 1990: 21594.

[9] 韩占忠，王敬，兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京： 北京理工大学出版社， 2004. 19-26.

[10] 高永海，孙宝江，刘东清,等. 环空水泥浆顶替界面稳定性数值模拟研究[J]. 石油学报， 2005， 26(5)： 120.

[11] 刘崇建. 油气井注水泥理论与应用[M]. 北京： 石油工业出版社， 2000. 295-307.

[12] 王伟，黄柏宗．高温高压下水泥浆的流变性及其模式[J]. 油田化学， 1994， 26(1)： 18.

[13] 高永海，孙宝江，赵欣欣，等.前置液流变性对顶替界面稳定性影响的数值模拟[J]. 中国石油大学学报：自然科学版， 2007， 31(6)： 51.

[14] 郑永刚，方铎，郝俊芳. 水平井注水泥的理论与实验研究[J]. 水动力学研究与进展， 1996, 11(1): 19.

[15] Jakobsen J, Sterri N, Saasen A, et al. Displacements in eccentric annuli during primary cementing in deviated wells[C]. SPE, 1991: 21686.

[16] 王秀文，刘巨保，黄金波，等. 固井过程套管串屈曲变形分析[J]. 石油矿场机械， 2011， 40(4)： 17.

SimulationAnalysisofCementingDisplacementinOffshoreExtendedReachWell

LI Hao1, WANG Jin-tang1, SUN Bao-jiang1, CAO Cheng-zhang2,LI Chun-li3, XU Ke-wang1

(1.SchoolofPetroleumEngineering,ChinaUniversityofPetroleum(EastChina),Qingdao,Shandong266580,China；2.InstituteofDrillingTechnology，SinopecShengliOilfieldServiceCorporation,Dongying,Shandong257017,China； 3.InstituteofGeology,ShengliOilProductionFactory,SinopecShengliOilfieldLimitedCompany,Dongying,Shandong257015,China)

Displacement efficiency and interface stability are critical to the success of offshore extended reach well cementing. According to the theory of computational fluid dynamics and the basic cementing data of extended reach well in South China Sea, the cement slurry rheological property and the influence of different borehole conditions on cementing displacement are obtained by numerical simulation. The calculations demonstrate that displacement efficiency increases with the increase of cement slurry consistency index and decreases with the increase of cement slurry flow index; well-cementing displacement efficiency first increases and then decreases and finally tends to be stable as the yield stress increases; the flow index of cement slurry should not be too high when cementing, and the value ofnshould be controlled within 0.6; the consistency index should be greater than 1.5 Pa·sn, but not exceed 3 Pa·sn; yield stress in the range of 10～18 Pa is advantageous to replace drilling fluid with the cement slurry. It is suggested that the eccentricity should be controlled within 0.5 as eccentricity has a great influence on the stability of interface; the stability of interface is obviously improved by using casing centralizer, and the optimized best rigid centralizer swirl angle is 60°; casing buckling, causing significant reduction of displacement efficiency in the annular interface, has a great influence on the stability of interface.

extended reach well; annular structure; displacement efficiency; interface stability; numerical simulation

P752; TE256

A

2095-7297(2014)01-0014-07

2014-02-22

国家科技重大专项(2011ZX05026-001-02)、国家863计划(2012AA091501)、教育部“长江学者和创新团队发展计划”(IRT1086)

李昊(1978—)，男，博士，讲师，主要从事油气井流动力学与工程及海洋石油工程方面的研究。