典型张力腿平台整体结构强度分析方法研究

李 阳，时忠民，谢 彬，谢文会

(中海油研究总院，北京 100027)

典型张力腿平台整体结构强度分析方法研究

李 阳，时忠民，谢 彬，谢文会

(中海油研究总院，北京 100027)

重点针对一种典型张力腿平台(TLP)进行了整体结构强度分析研究，以验证平台结构完整性设计的环境能够抵御恶劣海况的冲击。首先，建立了一种典型张力腿平台的整体有限元模型，平台主体结构按实际设计建立，上甲板结构通过甲板及梁模型对应简化。通过对操作和极端条件下载荷分析，得到平台危险波浪工况下载荷设计波参数。随后，将波浪载荷映射到整体结构的有限元模型，将张力腿上端位置建模简化为弹簧单元来反映包括旋转在内的6个自由度。最后，通过结构有限元计算软件得到结构在各危险工况下的最大等效应力及应力分布趋势，其中针对35个控制单元组，得到对应每种单元组的波浪的浪向及相位。分析结果及张力腿平台整体结构强度分析方法可供其他海洋平台强度分析参考。

张力腿平台; 整体结构强度评估; 极端工况; 有限元模型; 浪向

0 引 言

张力腿平台(TLP)整体结构强度分析对平台全寿命安全运行至关重要。整体结构强度分析的目的是确定在危险工况及环境载荷下平台结构的响应。根据TLP 的功能要求对其上部模块进行总体布置设计，最终确定了上部模块的尺寸以及质量和质量分布。该TLP 采用传统结构形式，四立柱、四旁通，立柱顶部用桁架连接。依据上部模块尺寸质量，对TLP壳体结构进行总体尺度规划，确定了平台总体尺寸；并对结构质量、可变压载质量、固定压载质量和附属构件质量进行估算，编制出总体质量控制报告；同时根据平台的处理能力以及天然气输送要求进行立管设计，确定出立管尺寸。张力腿作为TLP的系泊系统，在总体设计中要根据平台定位要求，确定其总体尺寸[1]。

1 分析对象与方法

1.1 分析对象

本文分析研究的典型TLP主要结构包括立柱、节点、旁通以及上甲板四部分。旁通为近似矩形截面的结构，高9.5 m，宽12.35 m。旁通与立柱之间通过节点进行连接。4个节点是高为9.5 m、外径为23.75 m的柱形结构。立柱顶端高度为57.45 m。平台的名义吃水为30 m。

平台舱室由于其功能性可划分为临时舱室、永久舱室以及空舱三种类型。典型张力腿平台各部分定义如图1所示。

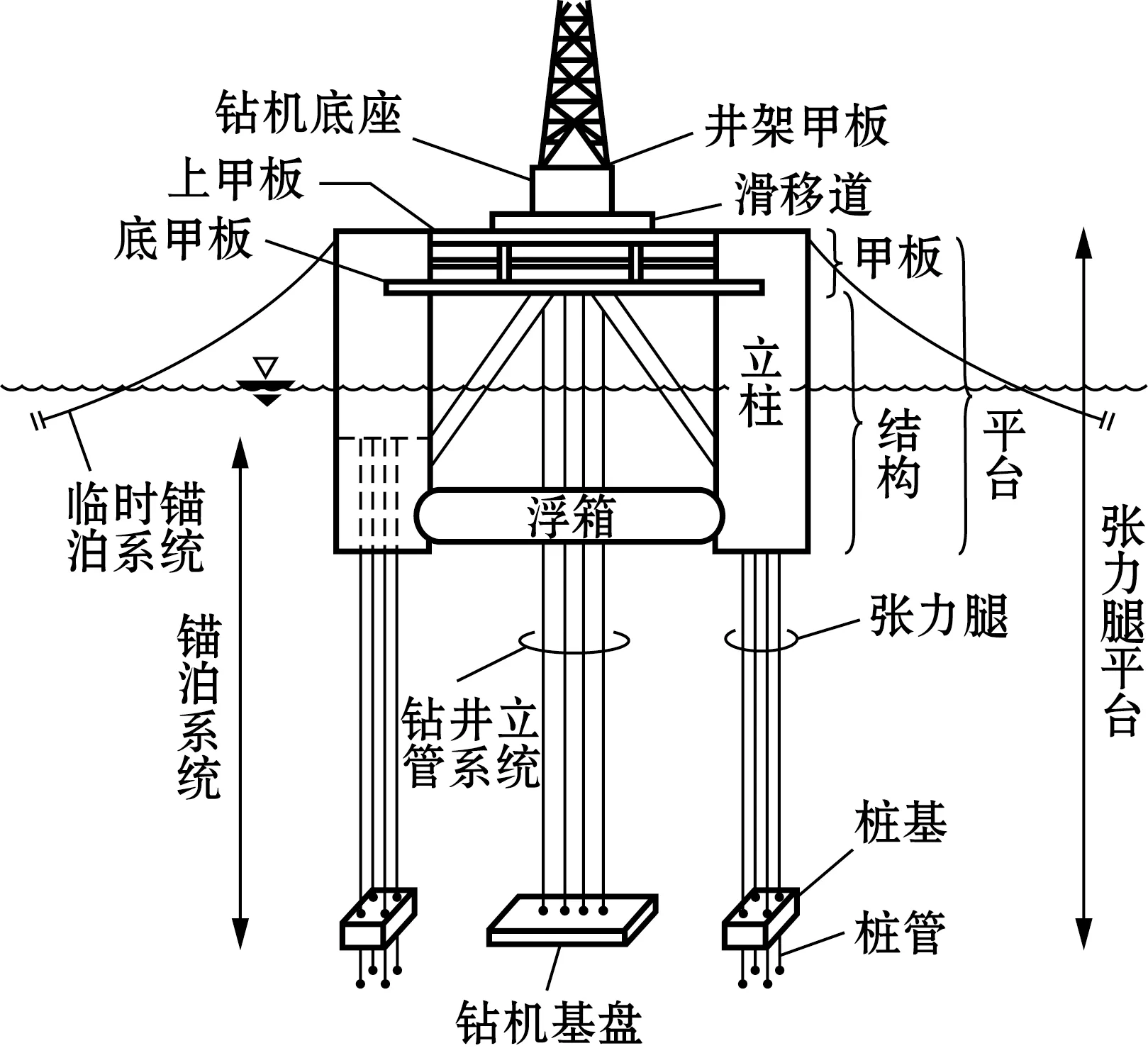
图1 典型张力腿平台各部分示意Fig. 1 Schematic of a typical TLP

1.2 分析方法

结构有限元分析载荷包括了静载、半静载以及动载荷三部分。针对平台六种典型的极端工况，最大横向撕裂力、最大横向扭矩、最大纵向剪切力、最大垂向弯矩、最大甲板纵向惯性力、最大甲板横向惯性力的设计波分析是首先计算的内容。

采用SESAM软件进行分析。建模中采用四节点平板单元、三节点平板单元、两节点梁单元、质量单元以及弹簧单元，建立平台整体结构有限元模型。弹簧单元用来模拟张力腿与平台接触位置的三维位移，刚度参考了张力腿的刚度及平台运动阻尼。

平台的坐标系统定义为：以平台主结构基平面几何中心为坐标原点，X轴正向指向平台东侧，Y轴正向向北，Z轴垂直向上。图2为平台危险工况及坐标系示意图[1]。

图2 典型TLP平台危险工况示意图Fig. 2 Typical TLP motion nomenclature

1.3 结构分析有限元模型

本文所研究的典型TLP采用DNV-SESAM的GeniE模块进行建模，模型的整体坐标系与平台坐标系统一致：以平台结构基平面几何中心为坐标原点。进行TLP平台总强度分析，验证平台浮箱、立柱及其连接结构的屈服强度是否满足使用要求。按照船级社要求，采用有限元方法计算平台总强度。采用壳单元模拟平台外板、甲板、舱壁、强框架腹板等结构，采用梁单元模拟扶强材、桁材等结构。水动力载荷、静水载荷和平台加速度基于设计波幅直接传递给平台总强度有限元模型，从而验证平台主体结构的屈服强度是否满足规范要求。

模型主要包括四个立柱、环形浮箱、立柱上部横向支撑和上部组块桁架结构。为保证分析结果的准确性及提高工作时效，在平台总强度分析中只建立基本结构的有限元模型(甲板、舱壁、大梁等)，不考虑局部集中载荷等因素所要求的局部结构加强。建模中考虑了部分简化处理，包括平台主甲板结构采用板梁组合的桁架式结构进行建模，上部设备采用质量点及调整板密度的形式建立，压载水舱质量采用调整所在舱室上下板密度方式建立。

图3为平台板厚分布图，图4为平台整体结构有限元模型，图5为平台整体结构有限元模型。

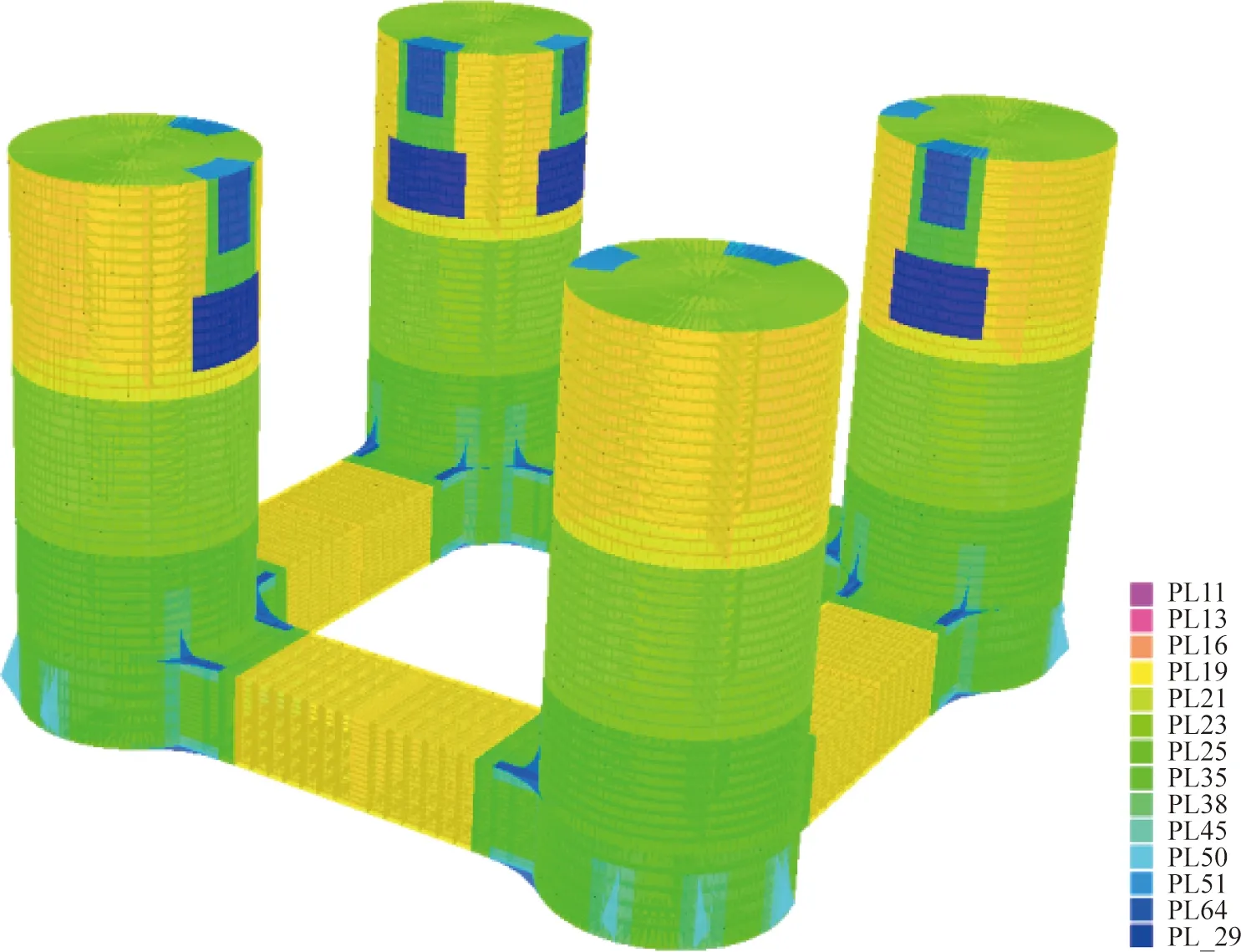
图3 典型张力腿平台主结构板厚分布Fig.3 Plate thickness of TLP hull

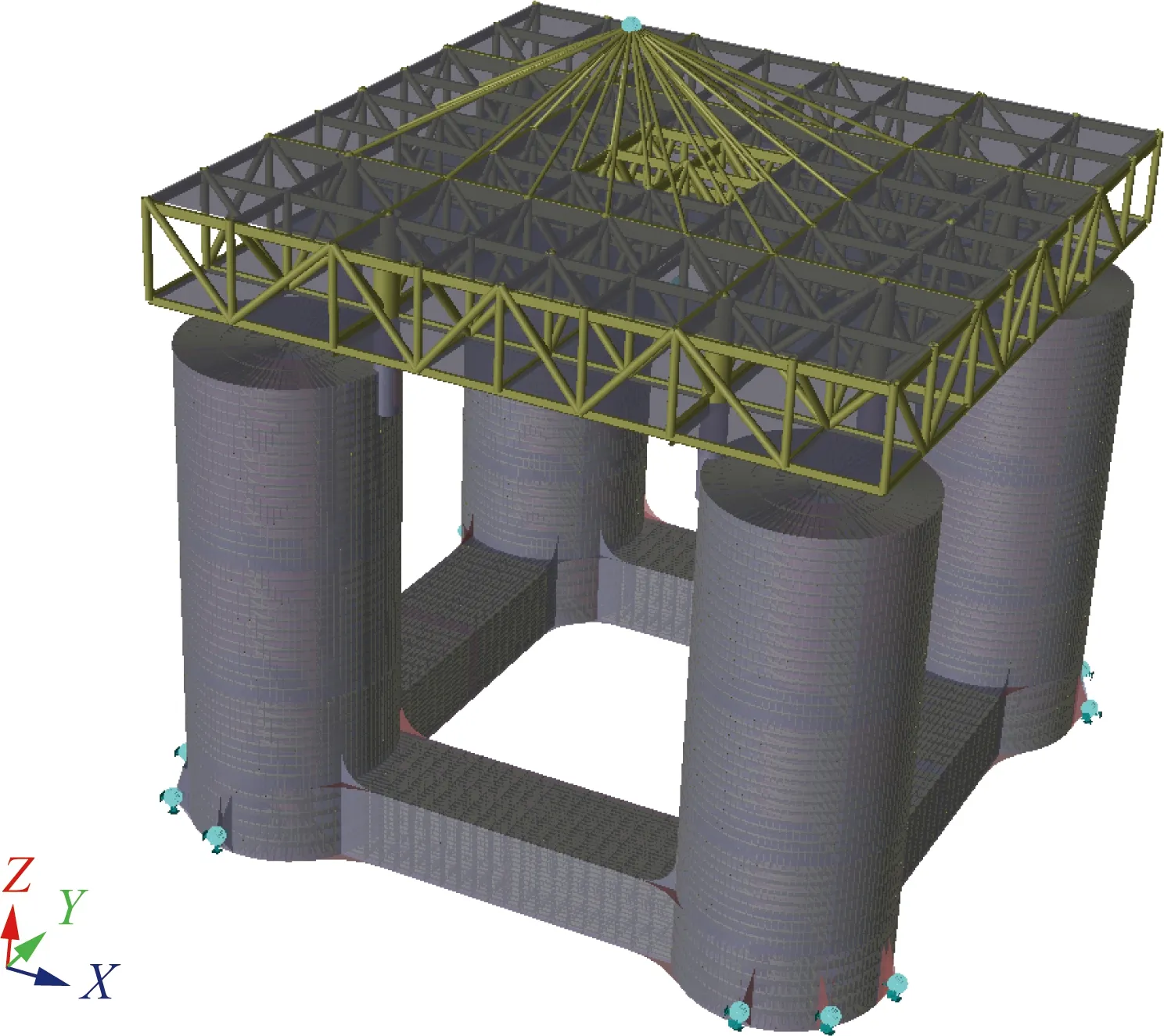
图4 平台整体结构几何模型Fig.4 Global structural model

图5 平台整体结构有限元模型Fig.5 Global TLP finite element model

1.4 假定条件

本文分析中采用了如下假设：

(1) 张力腿及顶张力立管(TTR)采用三维弹簧单元进行模拟。

(2) 非线性波浪对水线以上的结构的作用力被假定为虚拟载荷，波浪对结构的作用力转化为结构节点上的力传递[2]。

(3) 张力腿结构和TTR结构在整体运动分析中简化为1/3的质量点，用于模拟其运动对结构造成的惯性力的影响。

1.5 边界条件

整体结构有限分析中，采用了一系列6自由度的弹簧单元来模拟Tendon porch位置结构，弹簧的轴向刚度由实际结构计算得出，如表1所示。图6显示了TLP弹簧单元模拟的示意图。

表1 张力腿弹簧单元刚度

图6 张力腿边界条件设置Fig.6 Boundary conditions of tendon porch location

2 结构强度分析

2.1 重量控制

平台各工况重量计算是通过设计基础及规格书确定的，操作工况和钻井工况重量信息如表2及表3所示。TTR重量和上部井架通过质量点来定义。张力腿结构和TTR结构在整体运动分析中简化为1/3的质量点，用于模拟其运动对结构造成的惯性力的影响。本文分析的主要工况为一年一遇及100年一遇危险工况，进行结果对比分析。

表2 作业工况平台质量统计表

注：XCG,YCG,ZCG为重心坐标。绕重心旋转半径，X向为40.89 m，Y向为42.17 m，Z向为33.44 m。排水量73 432 t，质量与载荷73 432 t,吃水30.00 m，浮心高(KB)为12.38 m，重心高(KG)为31.77 m，初稳性高(GM)为4.26 m，横稳性高(BM)为24.0 m，自由液面修正(FSC)为0.38 m。

2.2 重量校准

通过结构有限元软件建立的平台有限元模型的重量信息通常会与各工况重量有较大差别，本文采用调整结构密度及添加质量点的方法来进行各工况的重量校准。重量调整过程需要分步进行：首先，调整平台整体密度以满足目标重量信息；其次，以张力腿上表面为基准分别将平台分割为上部和下部，用平台坐标X轴、Y轴将平台分为8块，分别调整Z向坐标、X向坐标及Y向坐标。

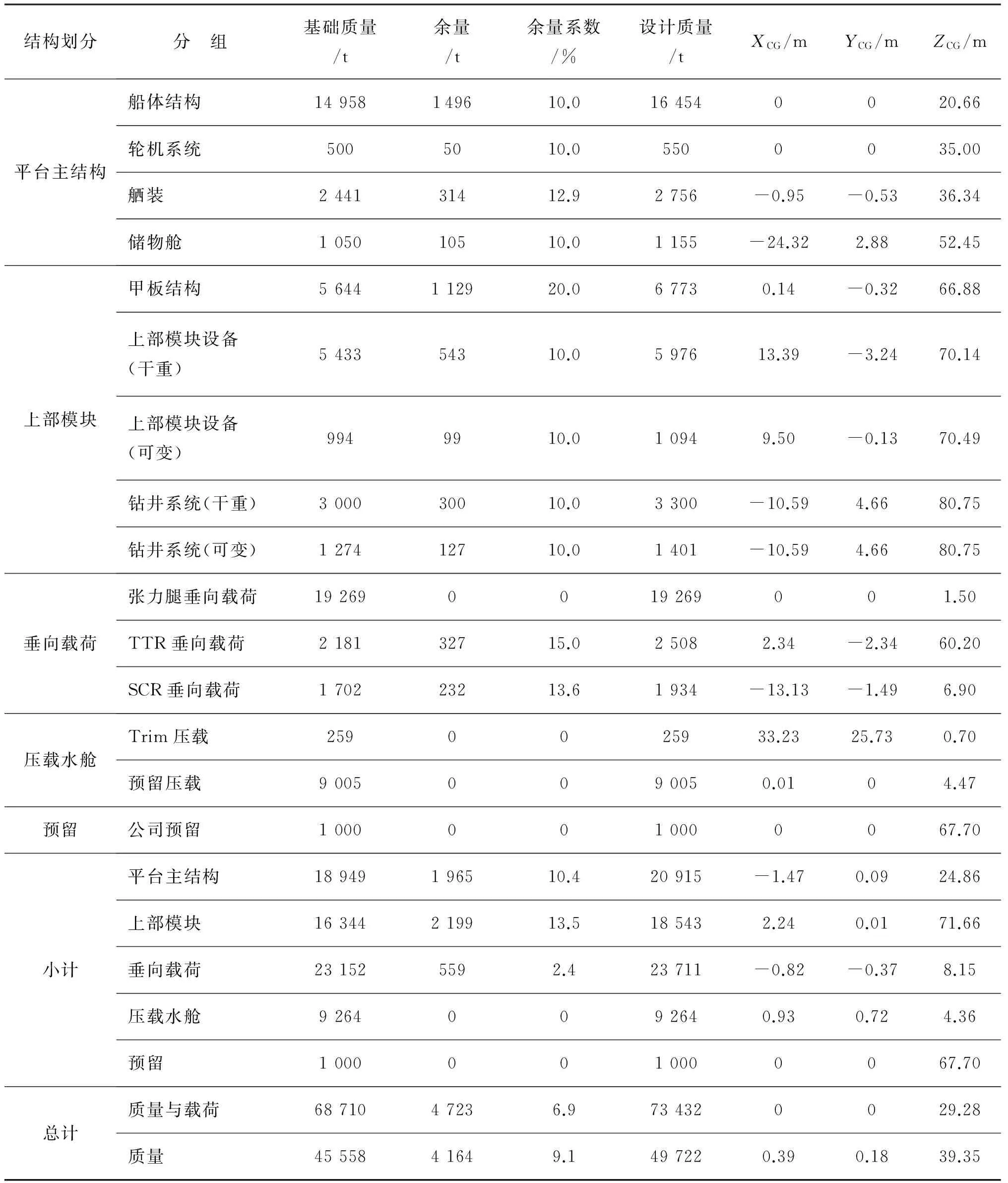
表3 极端工况平台质量统计表

注：绕重心旋转半径，X向为38.81 m,Y向为39.78 m,Z向为30.85 m。排水量73 432 t，质量与载荷73 432 t，吃水30.00 m，KB为12.38 m，KG为29.28 m, GM为7.00 m，BM为24.0 m， FSC为0.14 m。

调整后的钻井工况及操作工况的重量校准信息如表4及表5所示。

表4 极端工况下平台质量校准

表5 作业工况下平台质量校准

2.3 控制单元设置

将平台几何不连续、最危险等位置取为控制单元，以便更好地分析平台结构各处在各不同工况、不同相位的应力结果，该结果也可为局部分析提供基础条件。图7为选取的张力腿平台危险控制单元示意图。表6为本文定义的35个控制单元组。

2.4 设计波分析

TLP波浪载荷按规范规定采用设计波方法计算，分析内容包括横浪时的水平横向力和最大横向加速度、斜浪时的纵向剪力以及迎浪时的垂向弯矩和最大纵向加速度。采用设计波法计算TLP波浪载荷，需要确定各特征波浪载荷最大时的规则波周期、波幅、浪向和相位(即设计波参数)，进而确定特征波浪载荷极值，并进一步做结构分析。采用随机方法计算设计波参数，计算所得100年一遇极端工况及一年一遇操作工况设计波结果如表7所示。

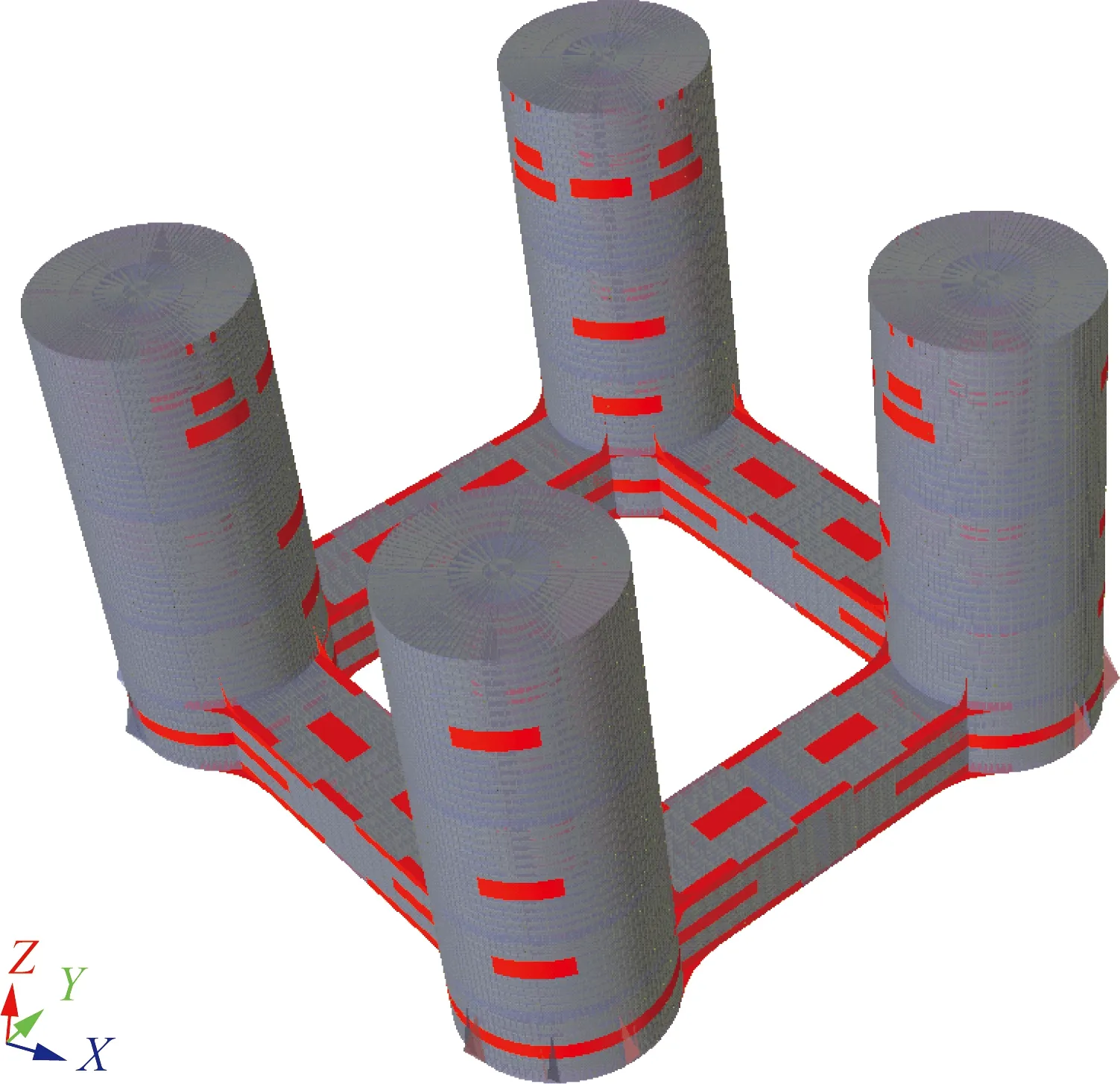
图7 TLP平台结构控制单元位置示意图Fig.7 Control groups position

整体分析中每种波浪工况包括了静载和动载两部分。静载包括了水压载荷、张力腿拉力、立管拉力等。水动力载荷通过SESTRA计算得出，为分析全面，浪向选择方面在0°～360°间隔45°，共8个浪向。

表6 控制单元组定义

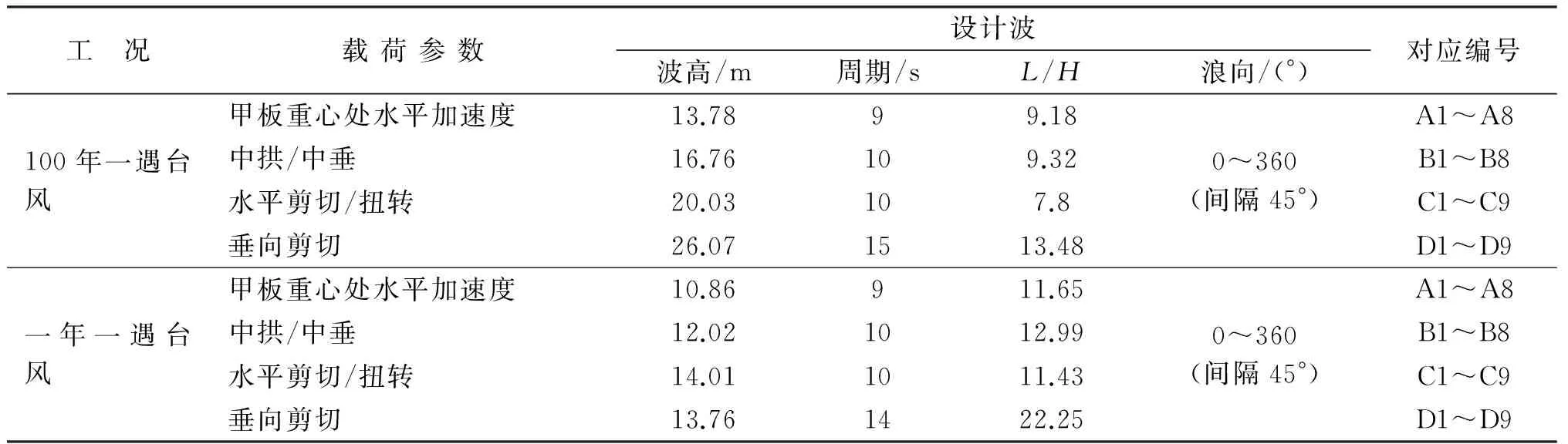
表7 平台设计波计算结果汇总

注：L/H为波长波高比。

一年一遇的工况组合中包括了一年一遇静载、一年一遇动载荷(实部和虚部组合)，100年一遇工况组合包括了100年一遇静载、100年一遇动载荷(实部和虚部组合)。

计算中静载和动载分别进行计算。在相位选择中，以2°步长在360°范围内进行搜寻。波浪载荷按规范规定采用设计波方法计算，计算海况按美国船级社(ABS)规范选取极限波陡为1/10。采用设计波法计算半潜式平台波浪载荷，需要确定各特征波浪载荷最大时的规则波周期、波幅、浪向和相位(即设计波参数)，进而确定特征波浪载荷极值，并进一步做结构分析。

采用三维势流理论计算了平台在单位波幅下的剖面载荷(最大横向力、最大横向扭矩、最大纵向剪力、最大垂向弯矩)的传递函数(RAO)、平台甲板底部最大横向和纵向加速度的传递函数。

静载和动载组合得到组合载荷，具体计算通过下式进行[3]：

σcomponent=σstatic+σRecosφ+σlmsinφ·Hd/2，

(1)

式中：Hd为波高；φ为相位。

计算波浪参数如表8所示。图8给出的是0°时的平台波浪传递云图。

表8 载荷组合

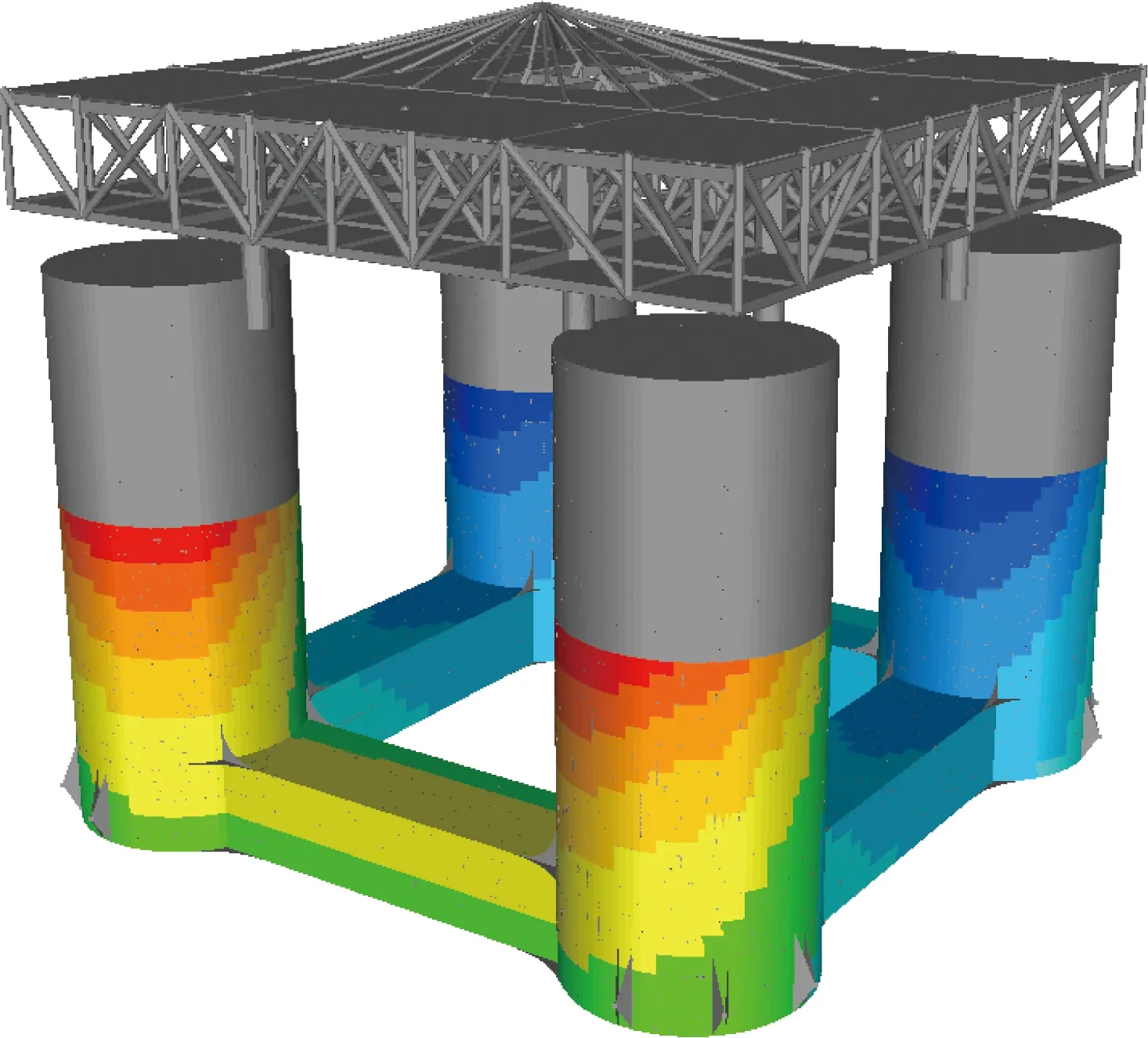
图8 平台波浪传递云图(0°)Fig.8 Typical wave loads to the TLP (0°)

3 结构强度分析结果

SESAM结构分析结果中包括了波高、相位、周期等信息，计算材料等效应力为345 MPa，依据规范[1-2]，一年一遇的安全系数取为0.7，许用应力为241.5 MPa，100年一遇的安全系数取为0.9，许用应力为310.5 MPa。

图9～12给出了分析所得平台各位置在极端工况下的应力分布。两种工况整体结构控制单元计算分析的结果如表9及表10所示。各部分结果汇总如表11及表12所示。

图9 极端工况下平台主结构应力分布云图Fig.9 Von Mises stress distribution of hull for 100-year load case

图10 极端工况下平台外表面应力分布云图Fig.10 Maximum Von Mises stress distribution of hull for 100-year load case

图11 极端工况下平台连接肘板等效应力Fig.11 Von Mises stress of pontoon gussets for 100-year load case

图12 极端工况下上甲板支撑结构Post等效应力Fig.12 Von Mises stress of column at upper post of 100-year load case

组号单元号等效应力/MPa计算值允许值安全因子相位角/(°)编号CG016428868.7241.50.28416C4CG02669750.5241.50.2094C8CG036403273.9241.50.30628C4CG04671662.7241.50.26040C4CG0571515214.2241.50.88736C3CG0655155204.7241.50.84834C5CG071127763.8241.50.264178C2CG089394699.7241.50.4130C8CG094230775.4241.50.31228C4CG101133697.1241.50.40240C4CG113101781.3241.50.33730C7CG1242310123241.50.50926C7CG134360080.7241.50.33430C7CG147153458.5241.50.24228C4CG1543578123.4241.50.51136C3CG16883688.4241.50.36644C4CG175515958.0241.50.2408C8CG1856077150.7241.50.62456C6CG1921980230.2241.50.95316C4CG20918650.5241.50.20914C8CG214904050.9241.50.21144C6CG222502108.5241.50.44930D3CG236942789.3241.50.37032C5CG2411002861.6241.50.25536C3CG2578811108.3241.50.44848C5CG266714493.4241.50.38756C3CG2710214944.3241.50.18352C3CG287258797.3241.50.40338C5CG2910749625.2241.50.10444C3CG3081025116.1241.50.48156C5CG3161956358.3241.51.48440C3CG3282456229.3241.50.94942C5CG337661564.6241.50.26728C3CG347774652.4241.50.21740C7CG358173052.4241.50.21740C7

注：屈服应力Fy=345 MPa; 安全系数为=0.9。

表10 极端工况下控制单元应力结果汇总

注：Fy=345 MPa; 安全系数为0.9。

表11 作业工况下平台各部分结构应力汇总

表12 极端工况下平台各部分结构应力汇总

计算结果显示：平台主体结构应力分布较为均匀，结构设计较为合理，仅立柱与上部组块、浮箱内侧与立柱外板连接处、平台基线至9.5 m高度范围、立柱内舱壁与立柱内板等连接处存在应力集中的情况，这些连接部位由于应力集中造成应力计算值较大，若在基本设计中进行局部结构优化设计或采用较高强度钢材即可满足许用应力要求。平台在百年一遇及一年一遇工况下旁通和立柱连接过渡肘板应力值较大。在上甲板与立柱连接的关键节点Post位置出现局部应力集中，如图12所示。在整体有限元模型分析中，此处没有建立局部加强构件。此问题可以通过局部有限元模型细化进行加强分析。

4 结 论

本文重点针对一种典型TLP进行了整体结构强度分析研究，建立了典型TLP的整体有限元模型，上甲板结构是通过甲板及梁模型对应简化得到的。在操作条件和极端条件下进行载荷分析，得到平台危险波浪工况下载荷设计波参数。将波浪载荷映射到整体结构的有限元模型，张力腿上端位置建模简化为弹簧单元来反映包括旋转在内的6个自由度，得出结构在各危险工况下的最大等效应力及应力分布趋势，得到了典型张力腿平台整体结构强度分析方法，可供其他海洋平台结构强度分析参考。

主要结论如下：

(1) 基于本文针对典型TLP整体结构强度分析发现，设计的平台整体结构强度满足规范的要求。

(2) 100年一遇波浪对平台扭矩更大，连接肘板承受力更大；而一年一遇工况下结构许用应力系数为0.7，所以该工况成为结构强度的主要控制工况。

(3) 由于旁通、立柱与节点过渡的连接肘板位置的特殊性等原因，在各计算工况中应力相对其他结构较大，所以在设计中应尽量增加对其结构加强的考虑。在100年一遇工况中，由于波浪力等作用力增大，平台旁通、立柱与节点的连接肘板应力相对其他工况较大。

(4) 周期在10 s左右的设计波为主要控制波浪。在局部结构强度分析中应加强对此周期范围的设计波分析。

[1] American Petroleum Institute. API RP 2T. Recommended practice for lanning, designing and constructing tension leg platforms[S]. Washington: American Petroleum Institute, 2010.

[2] American Petroleum Institute. API RP 2FPS. Planning, designing, and constructing floating production system[S]. Washington: American Petroleum Institute, 2010.

[3] American Bureau of Shipping. Guide for building and classing floating production, storage, and offloading systems[M]. Houston: American Bureau of Shipping, 1996.

GlobalStructuralStrengthAnalysisMethodologyofaTypicalTLP

LI Yang, SHI Zhong-min, XIE Bin, XIE Wen-hui

(CNOOCResearchInstitute,Beijing100027,China)

We focus on the global structure strength analysis of a typical tension leg platform (TLP). The objective of the TLP global structural analysis is to check the hull global structural integrity under design environmental conditions. Firstly, a global finite element model of the entire TLP is established, the hull structure is modeled in detail, whilst the deck structure is represented through a simplified deck beam model. A hydrodynamic analysis for operation and extreme conditions is conducted to get the design wave parameters for critical wave loads. After that, wave loads are mapped to the global structure finite element model, and the tendons are modeled as spring element which represents 6 degrees of freedom and rotations. Finally, the maximum stress and its distribution trends, together with the control elements, are obtained by finite element analysis according to critical wave heading, wave periods, wave heights and wave positions. Results and the TLP analysis method proposed can be used as reference for strength analysis of other offshore platforms.

tension leg platform; global structural strength analysis; extreme conditions; finite element model; wave heading

TE951

A

2095-7297(2014)01-0003-11

2014-01-22

国家科技重大专项(2011ZX05026-002)

李阳(1984—)，男，硕士，工程师，主要从事深水浮式平台结构及水动力分析方面的研究。