空间微振动模拟器柔性铰链设计

石 柱，徐振邦，吴清文，陈立恒

SHI Zhu, XU Zhen-bang, WU Qing-wen, CHEN Li-heng

（中国科学院 长春光学精密机械与物理研究所，长春 130033）

0 引言

空间高分辨率光学遥感器有重要的商业价值和军事价值，且迅速发展[1,2]。空间设施的微振动对其分辨率产生较大影响，对其振动特性进行研究从而实现有效隔振有重大意义。而空间微振动有微振幅、多自由度、随机、宽频的运动特点。

Stewart平台作为一种并联机构，由上平台、下平台和六根伸缩杆组成，下平台固定，通过控制六根支腿的伸缩实现上平台的六自由度运动[3]，可以有效模拟空间微振动。Stewart平台上下平台与伸缩杆关节处所用铰链的特性对于整个机构的动态特性以及控制特性有着至关重要的影响。传统刚性铰链，会产生摩擦和间隙，而柔性铰链具有无回退空程、无摩擦、高精度等优点，在实现精密定位和隔振平台也有着众多的应用[4]。柔性铰链可分为单向、双向和万向。空间微振动模拟器要实现六自由度的运动，根据并联机器人机构末端的运动特征是构成该机构的所有运动支链运动特征的交集理论[5]，单腿必须实现六自由度的运动特征，因此选用万向转动柔性铰链链。

万向柔性铰链在Stewart平台上作为隔振器和精确指向机构的应用，都仅考虑到铰链的转向能力（旋转刚度），而对轴向刚度的影响忽略[6]。对于微振动模拟器在高频振动时，不仅要求铰链有较低的弯曲刚度和扭转刚度，能有效实现关节的转动，也必须有高的轴向刚度，提高关节耦合处刚度，增强系统基频，使系统具有良好的动态特性和控制特性。而对于万向铰链，其轴向刚度、弯曲刚度及扭转刚度特性变化趋势一致（轴向刚度越大，弯曲刚度和扭转刚度也就越大），这和铰链设计要求相冲突。本文对直圆型万向柔性铰链刚度计算进行了深入研究，通过材料力学的公式计算分析铰链结构参数对各向刚度的影响，并辅助于有限元软件仿真进行验证，综合考虑铰链轴向刚度和旋转刚度要求，选取合理结构参数使得铰链满足指标要求，有较高的轴向刚度和较低的旋转刚度，对于万向柔性铰链的刚度设计有一定的指导意义。

1 设计思路与指标

依据仿真利用模型依据机构的运动指标要求提出柔性铰链的各向刚度要求，然后建立模型，用公式推导出来刚度与铰链结构参数的关系公式，得到刚度特性与结构参数的规律，利用有限元进行仿真计算验证。根据运动指标和材料强度参数确定柔性铰链的结构尺寸和刚度范围，确定了最佳结构参数，然后检验铰链取此结构是否满足刚度指标要求，之后对其强度进行了校核，完成铰链部分的结构设计。

微振动模拟器结构如图1所示，下平台固定，每个支腿都由一个音圈电机作为作动器，支腿和上下平台通过万向柔性铰链连接。模拟器上平台提供的振动指标要求为：六自由度、频率30Hz～400Hz，加速度保持在2×10-3g。

图1 微振动模拟器结构图

当模拟器高频振动时，如果铰链的轴向刚度低，使得支腿与平台耦合处容易发生共振，影响控制精度，甚至导致控制失稳。以极限高频400Hz振动为考虑目标，使关节耦合处不会发生共振，根据MATLAB理论模型换算出铰链的轴向刚度应高于3.4×104N/mm。

对于旋转刚度，较高则会产生力的干扰，影响动态特性和控制特性。若模型使用理想铰链，在平均工况（振动频率200Hz，电机力30N），铰链的弯曲角度和扭转角度分别为0.83’和0.037’。要求柔性铰链能达到理想铰链90%的转向能力，基于此，根据Matlab理论模型换算出铰链的弯曲刚度应低于2.45×105N·mm/rad，扭转刚度低于4.3×104N·mm/rad。

2 柔性铰链的刚度分析

直圆形万向柔性铰链，其结构如图2所示，在半径R的圆柱体的中间部分切半径r的槽，切槽部分厚度为t，三者关系为R=2r+t。由于设计的Stewart平台的结构尺寸限制，h取30mm，因此考虑R和t对铰链刚度的影响即可。铰链选取的材料为铍铜合金，弹性模量E=128GPa，泊松比ν=0.35，强度极限σS=1035Mpa，安全系数取n=2，[σ]=517.5Mpa，[τ]=362.25Mpa。

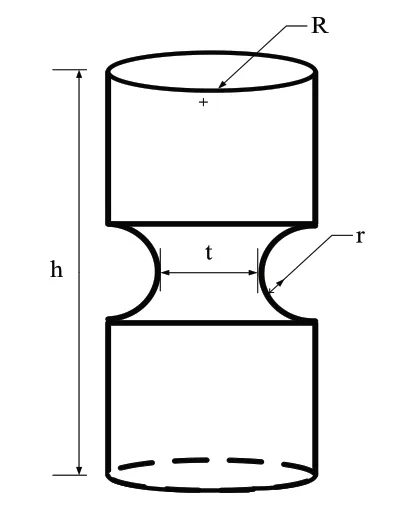
图2 柔性铰链结构图

2.1 轴向刚度

在铰链上端施加垂直载荷P，其轴向刚度为K，轴向变形为l，l1为P引起的铰链未切槽部分的轴向变形，l2为P引起的切槽部分（柔性部分）的轴向变形。根据材料力学公式：

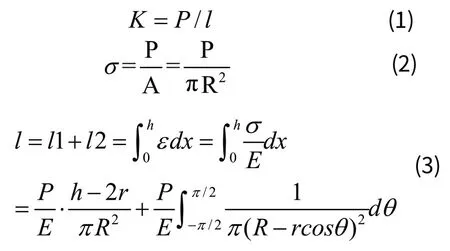
其中A表示未切槽部分横截面积，ε表示正应变，σ表示正应力。

利用MATLAB编写程序对其进行计算[7]。综合考虑R与t的影响，分别取R=5，6，7；t=1，1.5，2，2,5，3，3.5，4，4.5，5，5.5，6，8，10，单位为mm，作出R取不同值时，柔性铰链切槽部分和未切槽部分的轴向变形随切槽部分厚度t的变化曲线如图3所示。

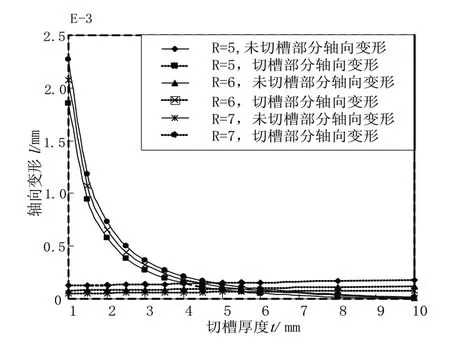
图3 轴向变形随切槽部分厚度t变化曲线

通过我们可以得出：

1）在h一定的情况下，柔性铰链的轴向变形，几乎不受半径R的影响，由切槽部分的厚度t决定。

2）在t大于5mm的时候，切槽部分的轴向变形和未切槽部分几乎无差别，而在t小于5mm的时候，切槽部分的轴向变形大于未切槽部分。

3）未切槽部分轴向变形几乎不受t影响，而切槽部分轴向变形随着t的变小呈指数型增长。

基于上述结论，取R=5mm。将切槽部分轴向变形和未切槽部分轴向变形相加得出其轴向变形l，根据公式（1）可以得出其轴向刚度K，作出其随切槽部分厚度t变化的曲线。为了验证理论推导的正确性，同时通过有限元分析软件Patran/Nastran对柔性铰链进行仿真。材料参数设置为E=128000MPa，ν=0.35，h=30mm，R=5mm，t分别1，1.5，2，2.5，3，3.5，4，4.5，5，5.5，6，8，10（单位为mm），建立单元数为29820的有限元模型，在上表面施加total load 60N，对其进行计算机仿真。然后提取轴向变形，并计算得到其轴向刚度，将其结果与理论结果相比较，得出结果如图4所示。

图4 轴向刚度随切槽厚度t变化曲线

通过仿真结果与理论计算的结果的比较，两条曲线基本一致，可以验证我们对于柔性铰链轴向刚度受结构参数变化的影响所作理论推导的正确性。分析曲线我们可以得出：轴向刚度随着切槽厚度t的增加成近似线性提高。

2.2 弯曲刚度

假定在铰链上端施加弯矩M，其弯曲刚度为Kθ，转角为θ，C为倒数弯曲刚度（定义为M引起铰链的转角与M之比，C越大）。根据材料力学公式：

上式中J(X)为铰链各部分截面惯性矩，C1为未切槽部分倒数弯曲刚度，C2为切槽（柔性）部分倒数弯曲刚度，其值越大，表示这一部分的弯曲刚度越小。利用MATLAB编写程序对其进行计算，分别取R=5，6，7；t=1，1.5，2，2,5，3，3.5，4，4.5，5，5.5，6，8，10（单位为mm），作出R取不同值时，柔性铰链切槽部分和未切槽部分的倒数弯曲刚度随切槽部分厚度t的变化曲线,如图5所示。

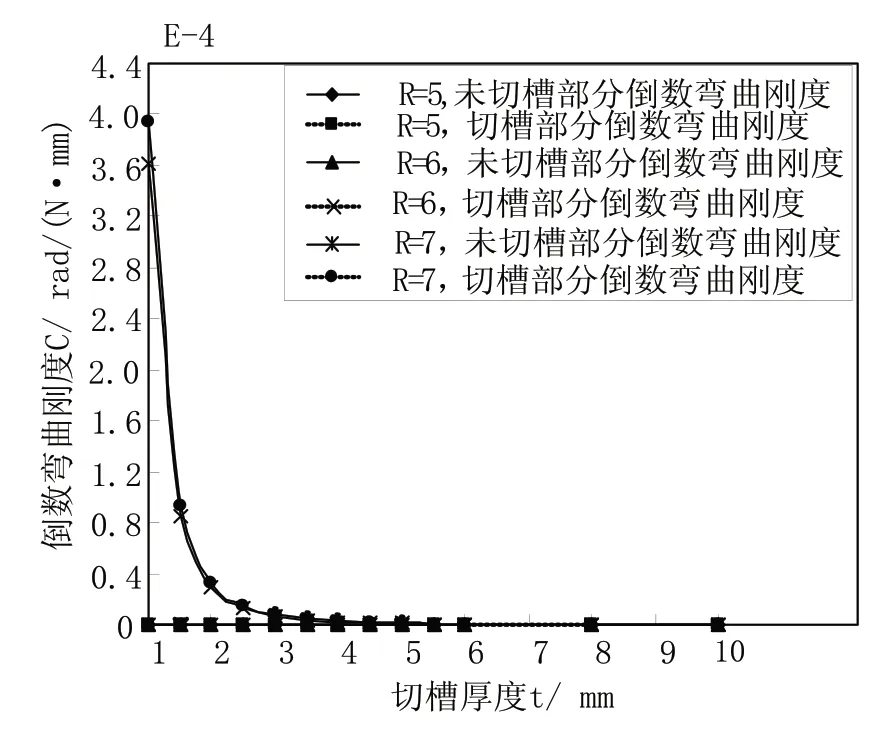
图5 倒数弯曲刚度随切槽部分厚度t变化曲线

通过上图我们可以得出：

在h一定的情况下，柔性铰链的倒数弯曲刚度，几乎不受半径R的影响，由切槽部分的厚度t决定。

在t大于4mm的时候，切槽部分的倒数弯曲刚度和未切槽部分都非常小，也就是铰链在M的作用下几乎没有弯曲。而在t小于5mm的时候，切槽部分的倒数弯曲刚度相对较大。

未切槽部分的倒数弯曲刚度几乎为0，切槽部分倒数弯曲刚度随着t的变小呈指数型增长。

基于上述结论，我们取R=5mm，并将切槽部分轴向变形和未切槽部分倒数弯曲刚度相加得出C，由，计算出弯曲刚度的值，作出其随t变化曲线。并利用Patran/Nastran有限元对其进行仿真（t=2时有限元模型如图7所示），给柔性铰链一端施加弯矩M，提取出断面的弯曲变形，再根据公式（4）求出其弯曲刚度，将仿真值与理论值相比较，结果如图6所示。

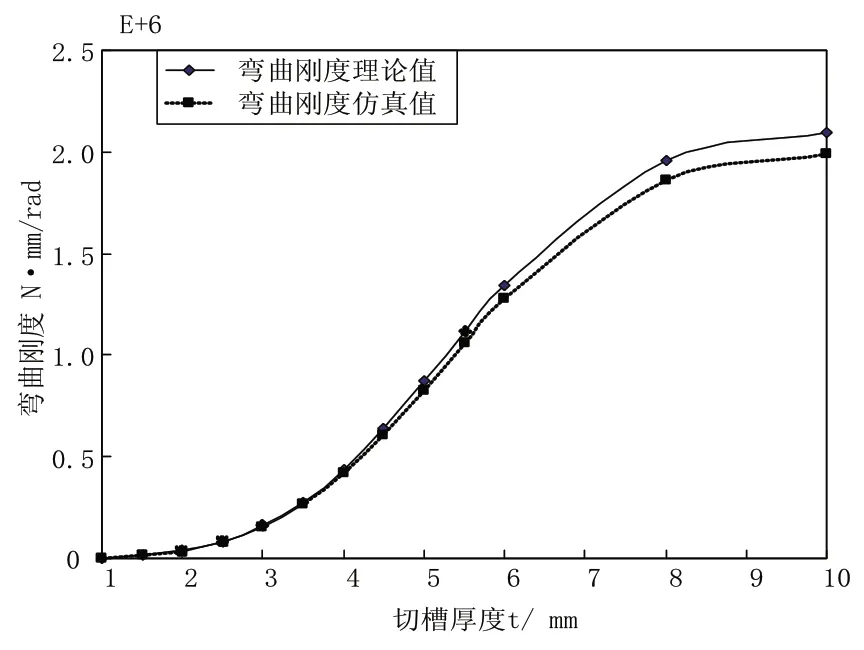
图6 弯曲刚度随切槽厚度t变化曲线

通过仿真结果与理论计算的结果的比较，可以再一次验证对于柔性铰链弯曲刚度因结构参数变化影响理论分析的正确性。观察弯曲刚度随切槽厚度t变化曲线可以得知：弯曲刚度的大小随着t的变大而几乎成指数型增长。

2.3 扭转刚度

当在铰链一端施加扭矩T时，铰链的扭转角为φ，根据材料力学公式：

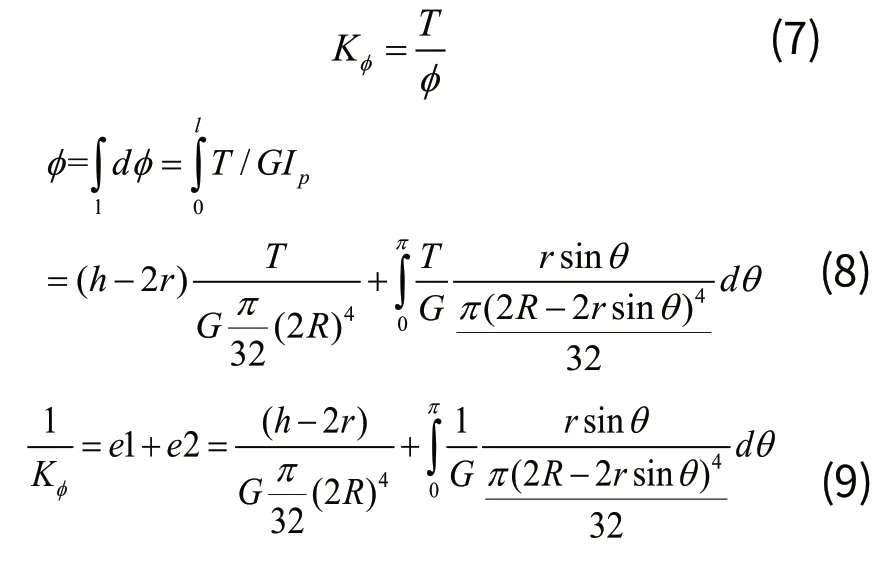
根据剪切模量G和弹性模量E的关系：G=E/2（1+ν），联立公式（9）和公式（6），可得e=C（1+ν），最终得出扭转刚度与弯曲刚度的关系式：

上式中，IP为截面极惯性矩，G为剪切模量，Kφ为扭转刚度，Kθ为弯曲刚度，ν为泊松比。由上公式我们可以看出扭转刚度和弯曲刚度之间是一个线性关系。材料铍铜合金ν=0.13，Kθ=Kθ/1.13。所以它随结构参数影响的变化趋势与弯曲刚度一致。

同样取R=5，计算Kφ理论值，分析其随t变化曲线，并同时利用Patran/Nastran有限元对其进行仿真，并且将理论结果与有限元结果进行比较，如图7所示。

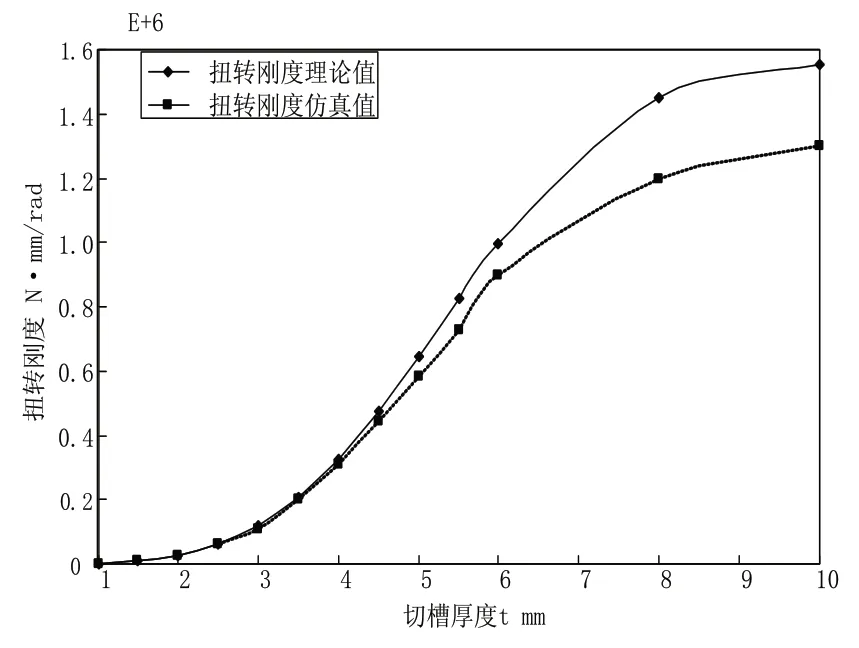
图7 扭转刚度随切槽厚度t变化曲线

理论值与仿真值的比较基本吻合，进一步说明理论推导公式结果的正确性。扭转刚度随切槽厚度t的变化趋势与弯曲刚度完全一致。

在得出柔性铰链的各向刚度随切槽厚度t的变化规律之后，再结合我们对柔性铰链的设计要求（较高的轴向刚度和较低的弯曲刚度与扭转刚度），可以得到下列思路：切槽部分厚度t越大，轴向刚度越大，旋转刚度也越大，这于结构参数的选择是一个矛盾。因此，要在轴向刚度和旋转刚度的设计中选取一个平衡：即选取合适的参数，使得旋转刚度满足要求的前提下，轴向刚度也尽量的大。

3 参数确定

在得出柔性铰链的各向刚度随切槽厚度t的变化规律之后，根据材料的许用应力和铰链的刚度指标要求确定结构的参数。

Stewart平台单腿电机驱动力最大取P=60N，单腿的最大弯曲角度和扭转角度为θ=±1°，φ=±1°，铰链材料取弹性强，强度高的铍铜合金，E=128GPa，v=0.35，σs=1035Mpa，安全系数n取2，[σ]=517.5Mpa，[τ]=362.25Mpa。

3.1 铰链的正应力

柔性铰链的正应力由其轴向的电机驱动力P和弯矩M产生。考虑运动和动力指标都取极限值的情况：P和M都取最大值，对其进行正应力强度校验，根据材料力学的公式：

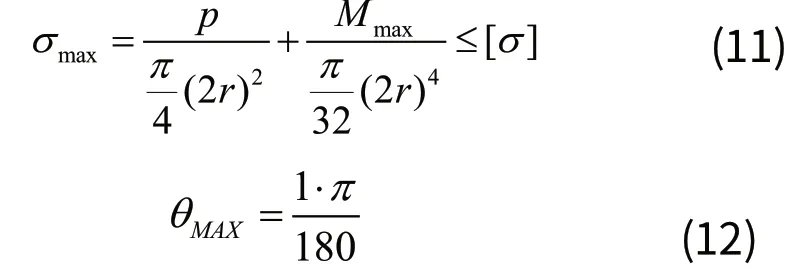
分别将t取不同值时对应的轴向刚度和弯曲刚度代入计算，由公式（4）计算出柔性铰链的最大弯矩，代入公式（11），得到在运动指标达到极限的时候，铰链最大正应力和切槽厚度t的变化曲线，如图8所示。

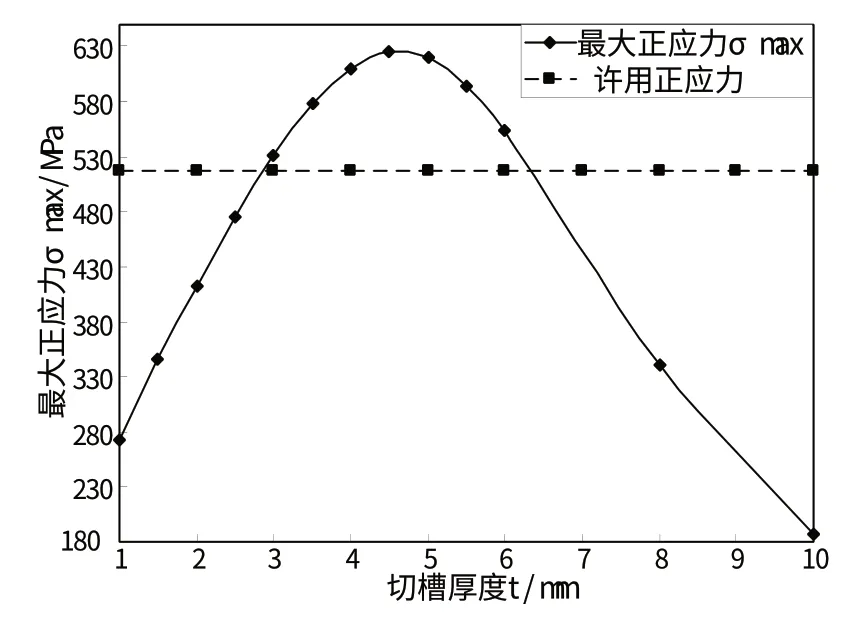
图8 最大正应力随切槽厚度变化曲线

3.2 铰链的剪切应力

铰链的剪切应力由转矩和扭矩产生，在运动指标取极限值的情况下，将t取不同值时，铰链的弯曲刚度和扭转刚度分代入下列公式计算，得到最大剪切应力和切槽厚度t的变化曲线，如图9所示。

上式中τ 1、τ 2分别为弯矩和扭矩产生的剪切应力。

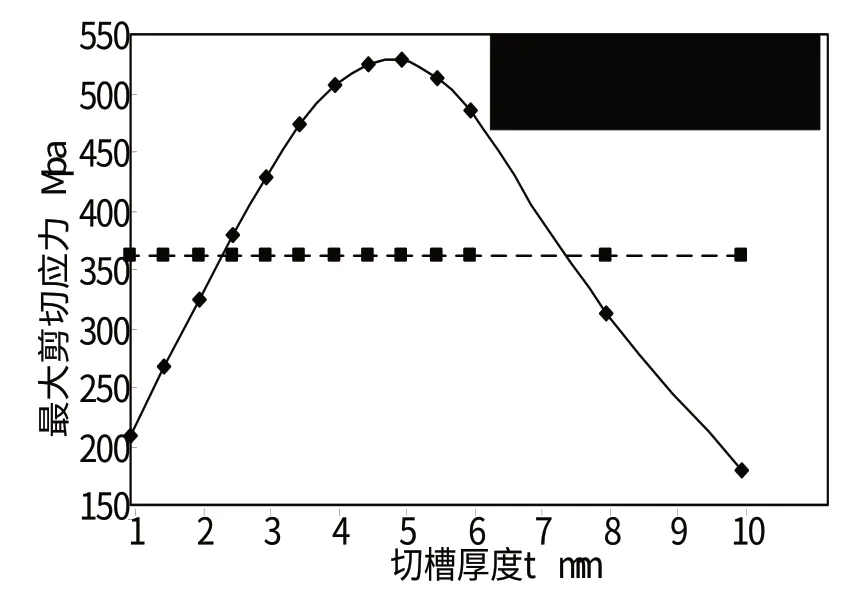
图9 最大剪切应力随切槽厚度变化曲线

由正应力和剪切应力的校验可以得知，要满足柔性铰链的强度要求，切槽厚度t，只能取1mm，1.5mm，2mm，8mm，10mm。结合第二节提出的指标：轴向刚度高于3.4×104N/mm弯曲刚度低于2.45×105N·mm/rad，扭转刚度低于4.3×104N·mm/rad，t=2mm，为最终柔性铰链参数选择。其轴向刚度为8.50×104N/mm，弯曲刚度为3.72×104Nm/rad，扭转刚度为2.75×104N·m/rad，均满足指标要求。

因此，对于柔性铰链的参数最终确定：h=30mm，R=5mm，t=2mm。

4 有限元校核

建立有限元模型后，给其同时施加极限动力指标和运动指标情况下的轴向轴向载荷PMAX，MMAX，TMAX，然后查看应力云图如图10所示。可以得知，最大应力发生在铰链切槽部分，其值约为300MPa，小于材料的许用应力，即强度校核满足要求，设计合理。

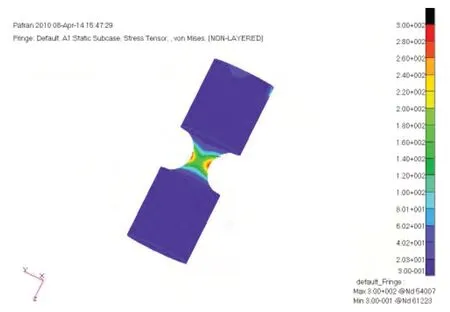
图10 强度校核结果

5 结论

本文基于Stewart平台作空间微振动模拟器的设计要求，选用万向柔性铰链作为机构关节。研究了万向柔性铰链各向刚度特性与其结构参数的关系，并结合整个Stewart平台结构运动学指标、动力学指标和强度特性对柔性铰链进行结构参数设计，然后用有限元进行校核，完成了用作空间微振动模拟器的Stewart平台的柔性铰链设计，且满足指标要求。

万向柔性铰链的刚度特性主要由切槽部分的厚度t决定，其轴向刚度和旋转刚度都随着切槽厚度t的增大而变大。对于Stewart平台的关节处，要求铰链的轴向刚度较高而旋转刚度较低。因此对其关键参数t的确定，需要结合具体运动指标、动力指标和材料强度特性进行分析。一般在满足材料强度特性的情况下，选取的切槽厚度t要使得旋转刚度尽量小而轴向刚度尽量大。

[1]ATAD E,et al..Atlast-9.2m:a large-aperture deployable space telescope[J].Proc.of SPIE,2010,7731,77312M1-10.

[2]叶伟楠,董吉洪.大口径主镜轻量化结构参数的优化设计[J].中国光学,2012,5(3):222-228.

[3]Stewart D.A platform with six degrees of freedom[J].Proc.Inst.Mech.Eng,1965,180(15):371-378.

[4]张定会.柔性铰链实现微位移的方法研究[J].工业仪表与自动化装置,1999,(5):11-13.

[5]Byung JY,Heung YN,Goo B C etc.Design and Experiment of a3DOF Parallel Micro-Mechanism Utilizing Flexure Hinges[J].IEEE International conference on Robotics and Automation,2002.

[6]高鹏,袁哲俊,姚英学.基于柔性铰链结构的新型双向微动工作台的研究[J].仪器仪表学报,1998,19(2):192-195 .

[7]刘伟,单轴柔性铰链转角刚度的计算机辅助计算仁[J].光学精密工程,2000,8(2):178-180.