卡尔曼滤波在GPS/SINS船舶组合导航中的应用

阎羡功

(江苏海事职业技术学院 经济管理学院，江苏 南京211170)

0 引 言

随着计算机、传感和信息技术的产生和发展给船舶导航技术中的导航精度的提高带来了新的开发途径［1-2］。目前，在船舶导航系统中应用最为广泛的系统包括全球定位系统 (Global Positioning System，GPS)［3］和捷联惯导系统(Strapdown Inertial Navigation System，SINS)［4-5］。前人的研究结果表明，GPS 和SINS 导航方式具有优势互补的特点。GPS 虽然定位精度较高，但因地域因素在地面信号的连续性较差，抗干扰性能差、易中断。SINS 采用主动导航方式，抗干扰能力强，虽然精度也比较高单因其数据传输方式等因素存在数据的累积误差。因此，组合GPS/ SINS 组合导航技术［6-7］应运而生并在这几年得到了快速发展。卡尔曼滤波［8-9］方法出现的初衷是为了解决维纳滤波方式的不足，现已发展成为一种典型的软件滤波技术，其滤波的基本策略如下:以数据方差的最小值为准则，有效利用相邻2 个时刻的估计值和测量值来优化对实际状态的估计。卡尔曼滤波技术已经在船舶导航系统的设计中取得了初步应用，但海洋环境变化异常，目前还没有一套较为完整的数学模型来对GPS/ SINS 组合导航中的数据进行准确的处理。本文首先对卡尔曼方法的基本原理进行深入探讨，分析了船舶导航的特点探索基于卡尔曼滤波的GPS/SINS 组合导航系统设计和应用方法，在此基础上，对组合导航系统进行仿真研究。

1 GPS/SINS 船舶组合导航系统模型

GPS 和SINS 组合导航能够充分利用各自的优势，有利于实现测量误差低、连续工作时间长、响应频率范围广的导航效果。松组合和紧组合是GPS和SINS 的组合导航的2 种应用方式，本文将分别对这2 种方式进行深入分析，建立其状态-观测传递函数。

首先，船舶的运动方程如下:

其中:t 为时间尺度;x (t)为系统状态量(属于矢量)，Φ (t +1，t)表示转换矩阵方程。船舶在海中气候和海洋环境复杂多变，因此其运动过程信号噪音较大，本文采用一阶Markov 方程进行建模，其方程表示如下:

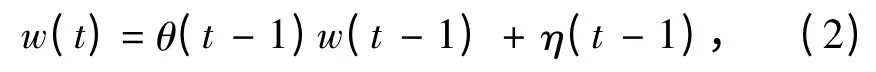
式中:η (t)为系统不规则随机误差值。系统中的GPS 和SINS 子系统经标准化后的各自测量方法如下式所示:

其中，υi(t)为各子系统相互之间独立的高斯白噪音信号，该信号的方差矩阵方程为:

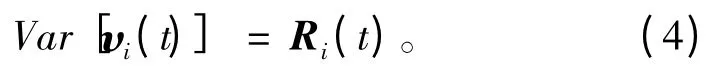
本文对所建立的导航系统进行了优化，经优化后的系统测量传递函数如下:

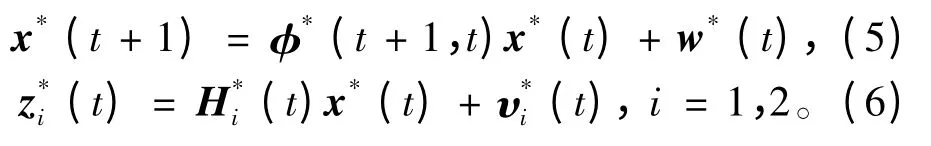
其中，

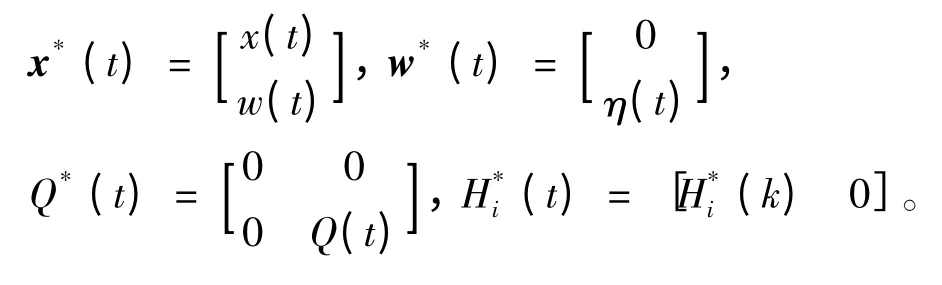
基于当地极地轴坐标系统，不紧密组合的状态传递函数如下:

式中:XI(t)为SINS 状态向量;FI(t)为SINS 状态矩阵;WI(t)为SINS 信号噪音;GI(t)为该噪音信号矩阵。结合系统信号误差方程可得系统观测方程为:

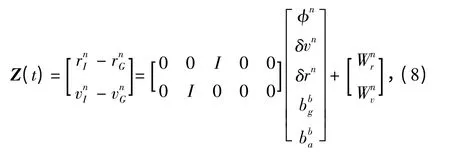
则所测船舶经纬度定位误差如下:

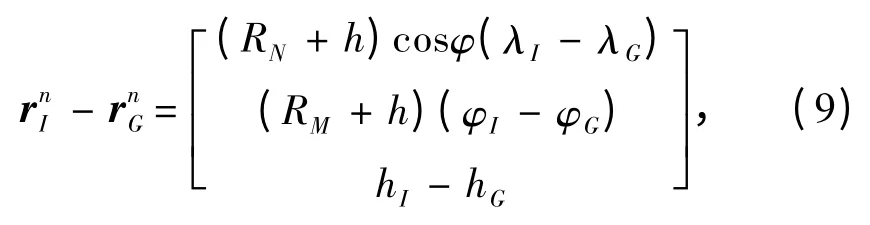
根据协方差的定义可得，在该组合导航中，系统的协方差方程如下:

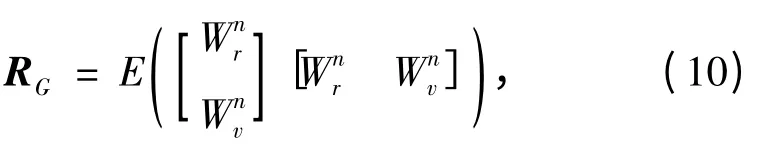
在理想条件下，RG为GPS 导航的协方差并采用加权置信方式，但在实际情况下，通常因该信息的输出量较微弱，因此将该数值定义为常量。

GPS 和SINS 紧组合状态模型如下:

式中:XG(t)为SINS 状态向量;FG(t)为SINS 状态矩阵;WG(t)为SINS 信号噪声;GG(t)为该噪声信号矩阵。

2 基于卡尔曼滤波的组合导航系统设计方法

卡尔曼方法对于line 系统数据处理效果更好，式(3)为一个简单典型line 系统的数学表示:

式中，Q 为系统测量数据均方差，

组合系统的测量方法可用式(13)表示:

对于nonline 装置，需要对卡尔曼滤波进行算法扩展，式(4)为一个简单典型nonline 装置函数的测量方法:

在GPS/SINS 导航装置中，卡尔曼算法是系统数据处理核心技术。该方法基于空间状态进行装置的表示，以数学递进函数为主要计算模式，因此，非常适合于计算机的编程和计算软件的设计。从本质上来说，卡尔曼滤波属于一种估算方法，其基本组成包括系统方程、观测方程和算法等，本文选用扩展卡尔曼滤波方法进行组合导航系统的设计。图1 为卡尔曼方法扩展原理示意图:卡尔曼滤波实现了状态更新和协方差更新，且状态矩阵和测量矩阵均作为卡尔曼算法的输入量。

图1 卡尔曼方法扩展原理示意图Fig.1 Kalman way extension principle diagram

从系统设计的角度，本文设计了自学习(或自适应)的卡尔曼方法，其结构如图2 所示。

图2 具有自学习功能的卡尔曼方法Fig.2 The function of self-learning kalman method

其传递函数为:

其状态估计为:

卡尔曼滤波算法在计算过程中存在误差积累性质，当处理的数据存在较小误差时，随着时间的积累，数据的误差因旧数据的存在而逐渐增大，甚至出现数据发散的现象。为了降低旧数据在误差积累中的权重，本文对记忆数据进行了衰减处理，从而提高整个算法的自适应性能。经纬度测量数据和坐标轴值误差大小数据处理流程如图3 所示。

图3 测量数据和坐标值数据处理流程Fig.3 Measurement data and coordinates data processing

考虑经衰减处理后的组合系统误差矩阵在计算机中仿真时易溢出，本文对测量数据进行加权处理，其示意图如图4 所示。其基本原理是将GPS 的测量数据经T 变换后与SINS 测量数据进行叠加，叠加后的测量数据分量导入卡尔曼滤波器的输入端。

图4 组合导航装置误差加权处理示意图Fig.4 Weighted combination navigation device error processing schemes

3 组合导航系统仿真及分析

在组合导航系统仿真过程中，取系统的当前位置变量为:

其中，xi，υi，ai分别为征空间坐标系中三维方向上的位移、速度和加速度。采用上述优化后的卡尔曼滤波算法数据处理的速度矢量仿真结果如图5 所示，由图中可以看出，集中式融合和顺序融合误差曲线均存在一定的波动，但绝对误差峰值较小，均方误差均为7.5632。

图5 两种融合方式绝对误差变化曲线Fig.5 Two types of fusion absolute error curve

图6 所示为GPS 和SINS 组合导航与单独SINS单个导航效果的绝对误差仿真结果比较，结果表明，整体上组合导航的误差较小，均方误差峰值仅为6.532 左右，而单独SINS 导航误差高达9.532。

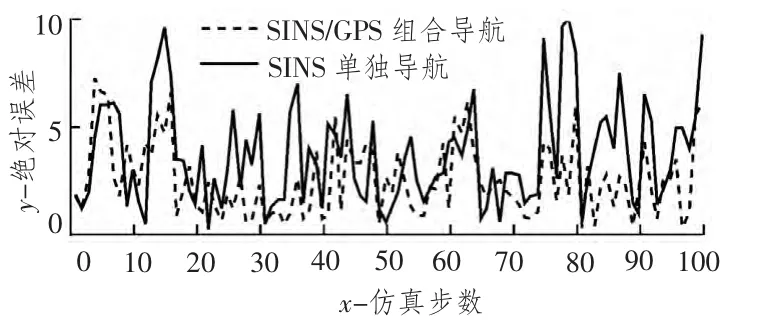
图6 组合导航与单独SINS 导航仿真结果对比Fig.6 The contrast of integrated navigation and SINS navigation simulation results

图7 为GPS 和SINS 组合导航与单独GPS 单个导航效果的绝对误差仿真结果比较，结果表明，整体上组合导航的误差较小，均方误差峰值仅为7.965 4 左右，而单独GPS 导航误差高达10.023。

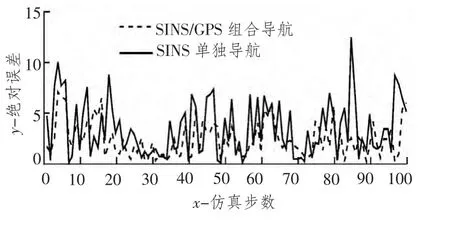
图7 组合导航与单独GPS 导航仿真结果对比Fig.7 The contrast of integrated navigation and GPS navigation simulation results alone

4 结 语

本文深入研究了卡尔曼方法和卡尔曼滤波经扩展后的性能方法的基本原理。结合海洋环境实际，探索了卡尔曼方法在组合导航中的应用策略，在此基础上进行了组合导航系统的设计和仿真。为了降低旧数据在误差积累中的权重，本文对记忆数据进行了衰减处理，从而提高整个算法的自适应性能。仿真结果表明，集中式融合和顺序融合误差曲线均存在一定的波动，但绝对误差峰值较小，均方误差均为7.563 2。经扩展和优化后的卡尔曼滤波，上述组合导航装置误差总体较小，均方误差峰值仅为6.532 左右，而单独SINS 导航误差约9.532，单独GPS 导航误差约10.023。

［1］MASARU M. Flutter and its application-flutter mode and ship navigation［J］. Journal of Wind Engineering and Industrial Aerodynamics，2013，122:10 -20.

［2］张崇猛，蔡智渊，舒东亮，等.船舶惯性导航技术应用与展望［J］.舰船科学技术，2012，34(6):3 -8.ZHANG Chong-meng，CAI Zhi-yuan，SHU Dong-liang，et al. Application and prospect of ship inertial navigation technology［J ］. Ship Science and Technology，2012，34(6):3 -8.

［3］PAULO M，JOANA F，LUISA B. Evaluating the feasibility of GPS measurements of SSH on board a ship along the portuguese west coast［J］. Advances in Space Research，2013，51:1492 -1501.

［4］王振桓，陈希军，曾庆双.基于导航坐标系的捷联惯导系统旋转调制分析［J］. 哈尔滨工程大学学报，2011，32(7):921 -926.WANG Zhen-huan，CHEN Xi-jun，ZENG Qing-shuang.Ship′s inertial navigation system rotating modulation based on navigation coordinates ［J］. Journal of Harbin Engineering University，2011，32(7):921 -926.

［5］LIU X X，XU X S，WANG L H.A fast compass alignment method for SINS based on saved data and repeated navigation solution［J］.Measurement，2013，46:3836-3846.

［6］赵琳，王小旭，丁继成，等.组合导航系统非线性滤波算法综述［J］.中国惯性技术学报，2009，17(1):46 -52.ZHAO Lin，WANG Xiao-xu，DING Ji-cheng，et al.Overview of nonlinear filter methods applied in integrated navigation system［J］. Journal of Chinese Inertial Technology，2009，17(1):46 -52.

［7］许昭霞，王泽元，吴振东.水下航行器导航系统的模糊自适应多模型滤波方法［J］.舰船科学技术，2014，36(8):71 -79.XU Zhao-xia，WANG Ze-yuan，WU Zhen-dong. Fuzzy adaptive multiple model filtering algorithm to navigation system of underwater vehicle［J］. Ship Science and Technology，2014，36(8):71 -79.

［8］李厚全，唐劲松，苑秉成. 基于快速卡尔曼滤波的SAS水下组合导航方法［J］.舰船科学技术，2010，32(2):40-43.LI Hou-quan，TANG Jin-song，YUAN Bing-cheng. The research of the integrated navigation underwater on synthetic aperture sonar［J］.Ship Science and Technology，2010，32(2):40 -43.

［9］宋伟，周红进，王秀森.Kalman 滤波应用于GPS 相对导航信息解算方法［J］.舰船科学技术，2013，35(6):65-68.SONG Wei，ZHOU Hong-jin，WANG Xiu-sen. Research on relative navigation method based on GPS using Kalman filter［J］. Ship Science and Technology，2013，35(6):65-68.