离散复杂动态网络的一种非脆弱同步算法

张 丹

(西安电子科技大学理学院，陕西西安 710071)

随着复杂网络理论被广泛应用于物理、生物、经济、数学等多种学科［1－2］。人类对各种人工和自然的复杂网络的结构、性质和功能有更清楚的认识。多年来复杂网络研究的一个主要课题就是关于复杂网络的同步研究［3］。同步是一种复杂网络中普遍的非线性现象，实际生活中的许多网络也都表现出较强的同步倾向性。众多研究工作均是针对微软时变耦合网络的同步问题来展开的［4－5］，在已有的研究文献中，同步算法大致可分为以下两种:基于Lyapunov稳定性判据的同步算法法和基于连接图判据的同步算法。本文降低了复杂网络达到同步的条件，给出了一类离散时间系统复杂时变网络的加性非脆弱同步控制策略，得出算法中反馈增益矩阵的LMI算法，同时利用Lyapunov稳定性理论证明了该算法之下的复杂网络是非脆弱渐进同步的。

1 基本概念和引理

该部分列出了下文所用到的一些引理。

引理1［8］对于满足FTF≤I的任意矩阵F，有对任意给定的向量x∈p，y∈q以及常数ε＞0均成立，其中D和E是适当维数的常数矩阵。

引理2［9］设E，H，F是适当维数的实矩阵且满足FTF≤I，则对于标量ε＞0，有不等式成立

引理3［8－9］设 A，D，E，F 是适当维数的时矩阵且满足FTF≤I，则有矩阵P＞0，对于标量ε＞0且满足εI－DTPD＞0，则有不等式成立

(A+DFE)TP(A+DFE)≤ATPA+ATPD(εIDTPD)－1DTPA+ εETE

引理4［9］对于给定的矩阵，其中S11是r×r维的，则以下3个条件是等价的

(1)S＜0;

引理5［8］对于给定的实矩阵G和E，以及适当维数的对称阵S，下面的矩阵不等式成立

其中，F(k)满足F(k)TF(k)≤I，当且仅当对于某个ε ＞0，有

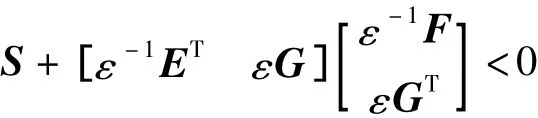
2 时变复杂网络模型

对于网络中的每个个体用xi(t)表示其状态，其可表示该结点的某些物理量，例如姿态、位置、温度和电压等。网络中的每个个体的状态和其周围的个体状态有关，即网络中每个个体的状态是由其自身的状态以及周围的个体状态所决定的，故而可用单积分微分方程(1)来表示该网络的状态［11］

其中，ui(k)，i=1，2，…，n 可称之为协议或算法，是一个待设计的状态反馈。

文中，研究一个线性耦合系统，即满足协议为以下方程的系统

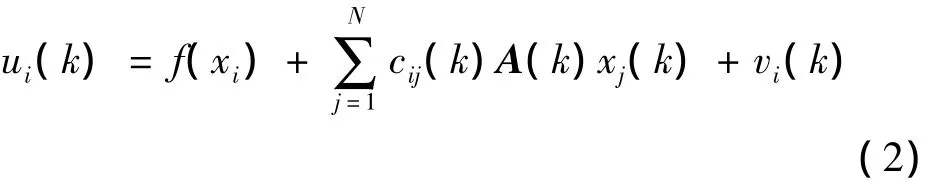
即

其中，vi(k)是待设计的反馈控制。i=1，2，…，N，xi=［xi1，xi2，…，xin］T∈n为网络中第 i个结点的状态变量。A(k)=［aij(k)］∈Rn×n为复杂网络在k时刻的内部耦合矩阵。耦合配置矩阵C(k)=［cij(k)］∈Rn×n表示网络在t时刻的拓扑结构和耦合强度，其对角线元素可如下定义表示结点i的状态xj(k)受其邻居结点的状态影响［11］。

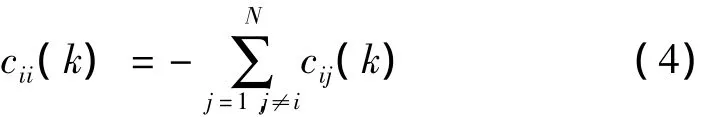
为后续讨论，首先给出几个假设条件:

假设1 网络模型式(3)的耦合矩阵C(k)的各元素均有界，即满足cij(k)≤c，其中c为正常数。

假设2 网络模型式(3)的耦合矩阵A(k)满足如下条件

其中，A0，E，H为常数矩阵;F(k)是时变矩阵并满足FT(k)F(k)≤I。

本文的目标是对每个结点设计合适的反馈控制率vi(k)，使得对于任意初始状态X0，网络式(3)总可实现渐进同步，即对初始状态X0，有

则称网络式(3)在反馈控制率vi(k)的控制下关于xi(k)=s(k)实现了渐进同步，其中xi(k，X0)表示以X0为初始状态的网络第i个结点的状态变量，s(k)为网络的同步轨迹，并满足如下条件

若记ei(k)=xi(k)－s(k)，考虑到如下等式

则带有控制的余差状态方程可描述为

其中∀i=1，2，…，N，f^(k)=f(xi(k))－ f(s(k))，系统式(7)是稳定的当且仅当下式成立

3 复杂动态网络非脆弱同步控制

针对复杂时变动态网络式(3)，耦合矩阵C(k)若有界且A(k)满足上述假设中的条件时，文中可利用非脆弱控制算法对该系统进行控制。

对于余差状态方程式(7)，采用加性摄动非脆弱控制

其中，K是待设计的矩阵。ΔK(k)=E0F(k)H0，E0和H0为常数矩阵。F(k)是时变不确定矩阵且满足FT(k)F(k)≤I。下面采用 Lyapunov方法来设计矩阵K。

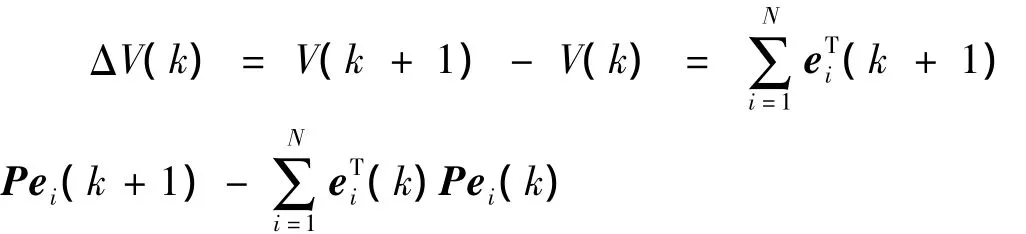
根据引理1，同时f(·)满足Lipschitz条件时，可得

其中，λ =λmax(P)，P －λI＜0。注意到A0+EF(k)H，根据Lyapunov判据，系统式(7)渐进稳定，若下式成立综合利用上述引理，推导可得式(11)成立等价于下列不等式成立

综上可得到复杂网络系统式(7)达到同步的充分条件是不等式(12)成立，即以下定理成立:

定理1 在施加了加性摄动非脆弱同步控制式(9)的情况下，时变线性耦合的复杂网络式(3)实现同步的充分条件是对于一个给定的正常数 ε、ε1，式(12)有可行解W和P，进而反馈增益矩阵K为K=P－1W。

4 结束语

研究了一类复杂动态网络的非脆弱同步算法，在考虑了网络的同步轨迹及拓扑信息后文中假设网络的耦合矩阵均有界的前提下，通过引入恰当的反馈控制策略，设计了加性的非脆弱反馈控制方案，并利用Lyapunov方法给出了网络实现渐进同步控制所需满足线性矩阵不等式(LMI)的条件，同时通过Matlab中的LMI工具箱求解出反馈增益矩阵K。经验证文中提到的方法在实际情况中更易实现，且网络节点的耦合强度、网络的拓扑结构等均具有较强的鲁棒性。

［1］ZHOU J，LU J，LU J.Adaptive synchronization of an uncertain complex dynamical network［J］.IEEE Transactions on Automatic Control，2006，51(4):652 －656.

［2］LU J，CHEN G.A time － varying complex dynamical network model and its controlled synchronization criteria［J］.IEEE Transactions on Automatic Control，2005，50(6):841 －846.

［3］汪小帆，苏厚胜.复杂动态网络控制研究进展［J］.力学进展，2008，38(6):751 －765.

［4］GUO W，AUSTIN F，CHEN S，et al.Pinning synchronization of the complex networks with non－delayed and delayed coupling［J］.Physics Letters A，2009，373(17):1565 －1572.

［5］WANG X F，CHEN G.Synchronization in small－ world dynamical networks［J］.International Journal of Bifurcation and Chaos，2002，12(1):187 －192.

［6］LV J，CHEN G R.A time － varying complex dynamical network model and its controlled synchronization criteria［J］.Transactions on Automatic Control，2005，50(6):841 －846.

［7］王磊，戴华平，孙优贤.时变复杂动力学网络的同步控制［J］.控制理论与应用，2008，25(4):603 －607.

［8］ZHANGGuo，LI Junmin.Non － Fragile guaranteed cost control of discrete－ time fuzzy bilinear system［J］.Journal of Systems Engineering and Electronics，2010，21(4):629 －634.