基于混合粒子群算法的企业订单分配优化研究
2014-12-18吴鸿辉江小云
陈 频,吴鸿辉,江小云
(1.厦门理工学院 管理学院,厦门 361024;2.台湾中华大学 企业管理学系,台湾 300012)
0 引言
发光二极管(Light-Emitting Diode,LED)产业由于具有节能环保特性在我国处于快速成长阶段,产业链包括原材料、上游的磊晶片制造、中游的芯片制造和下游的产品封装。一般的LED芯片厂商将上游和中游整合制造,成为LED产业很重要的一环。LED芯片厂的生厂过程分为两部分,包括前端和后端。前端主要生产磊晶片,后端将晶片加工成芯片,并经由点测、切割、分类和包装,最后入库或出货。一片磊晶片可产出成千上万颗结构、大小、电性功能不等的芯片。芯片中电性功能(分亮度和波长)的分布与前端的磊晶片的制造过程相关[1~3],由于生产过程的不稳定特性,满足投产工单的电性需求规格的芯片数量占的比例(即合工单率,Hit Target)普遍不高,导致产生很高的副产品库存。然而,这些副产品库存并不是残次品,它们可以满足其他的订单。因此如何合理地分配订单,有效地安排生产,最大幅度地降低库存水平,是LED芯片厂所必须面对的问题。
1 LED芯片厂的订单分配问题
LED芯片厂一般将芯片按其不同的电性功能以不同的区段(BIN)来分类。表1所示为一家LED厂的黄光芯片不同电性组合的BIN存货表,共9种BIN,括号中所注为BIN的编号。电性功能主要分为波长和亮度。黄光LED 的波长为584nm~588nm,分三种波段,亮度为0mcd~300mcd,分三个等级。客户下单时的订单规格,是以各电性范围来表示,例如客户A的订单要求规格为波长587nm~594nm,亮度为100mcd~300mcd,数量为800K。如表1的灰色部份所示,有4种BIN满足需求,即{(2,2),(2,3),(3,2),(3,3)}。由于分配给客户的BIN若越集中,则表示品质越好,价格应更高,因此出货时最好满足需求的BIN都出一些,不要为零或太低,否则会造成升级的问题(例如客户下次要求一样的品质)。要满足一张订单的规格和数量,有无限种BIN芯片数量的组合可满足,应如何选取最佳的BIN出货组合?也就是如何能让更多的订单可出货[4~7]。例如上述客户A的订单,如果出货时满足订单规格的4个BIN出货量各为200K,则出货后4个BIN的存货数量分别为(263,212,201,179)。如果还有另一客户B,订单要求规格为波长584nm~591nm,亮度为200mcd~300mcd,数量为600K,则因满足规格的2个BIN,即{(3,1),(3,2)}的存货总计只有543K,无法满足这张订单的需求,生管只能下工单安排生产。但是如果客户A的订单BIN(3,2)少出货100K,而让其他3个BIN多出货100K,则剩余的存货即可满足客户B的订单需求。因此,选择最佳的BIN订单分配组合,不但有助于存货的有效利用,而且能大幅提高客户的满意度。
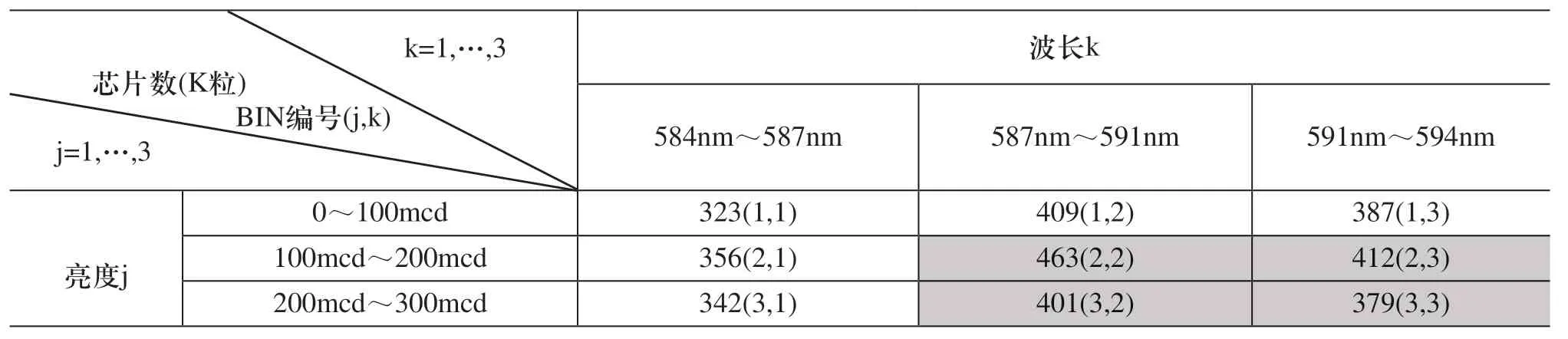
表1 LED芯片厂的黄光芯片各BIN期初库存
2 订单分配优化模型
假设LED芯片的亮度等级有J个等级,波长分为K种波段,总共有J ×K 个BIN,各BIN编号用(j,k)表示,j=1,…,J,k=1,…,K。 bjk表示BIN编号为(j,k)的初始库存。有I张订单须分配,订单i(i=1,…,I)的需求数量为qi,需求波长波段等级范围k为wil~wui,亮度等级范围j为 lil~lui,则LED芯片厂的订单分配优化模型可以描述如下。
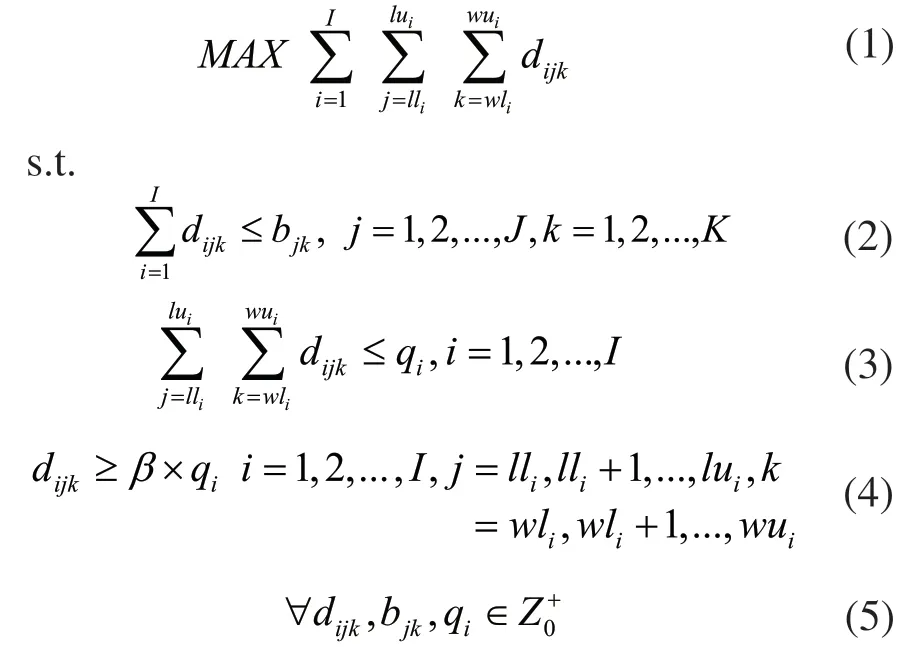
决策变量 dijk为分配给订单i的亮度等级编号为j,波长波段编号为k的BIN的出货量。式(1)为目标函数,表示出货量需最大。希望通过各决策变量 dijk的优化,找到最佳BIN出货组合,让尽可能多的订单出货需求得到满足。式(2)为第一类约束条件,共J ×K 个不等式,表示对于每一个亮度等级编号为j,波长波段编号为k的BIN,I张订单的总出货量不能大于其库存量。式(3)为第二类约束条件,共I个不等式,表示对于每一张订单,其出货量不能超过需求量。式(4)为决策变量的取值范围下界约束,即为避免问题升级,出货时每个BIN都要出的最少数量。式(5)表示各决策变量、各BIN库存量和各订单需求量须为正整数。
上述模型的决策变量值需为整数,属于整数规划模型,具有NP性质[8]。对于小规模整数规划问题,可以通过使用隐枚举法、动态规划方法、分支定界法等传统方法来求解[9],而对于中等规模甚至大规模问题,计算量会出现组合爆炸的现象,很难在合理的时间内求得模型最优解[10]。上述模型由于变量和约束非常多,且随着问题规模的变大会急剧增加,再加上决策变量属三维结构,增加了模型求解的难度,不适合使用传统方法求解。智能优化算法较常应用于中大规模的整数规划求解[11,12],因此针对该模型的特点,本文提出了基于转换矩阵的一种编码方法,将三维决策变量转换为二维矩阵,而后形成一维决策变量,使用混合粒子群算法进行求解,不仅降低了算法计算过程的复杂度,而且提高了求解效率。
3 求解订单分配优化模型的混合粒子群算法
使用标准粒子群算法求解时,随着迭代次数的增加,在种群快速收敛集中的同时,各粒子越来越来相似,算法很难跳出这个局部最优范围,即早熟收敛[13,14]。混合粒子群算法引用了遗传算法中的交叉和变异操作,不仅增大了种群的多样性,也有利于算法的全局搜索[15]。因此,本文提出了使用混合粒子群算法求解该订单分配优化模型,具体步骤如下:
步骤1:生成转换矩阵。决策变量 dijk属于三维结构,本文引入一个二维矩阵S(如式(6)所示)将三维变量转换为二维矩阵,最后形成一维决策变量求解。

其中矩阵中i表示订单号,每一行代表一张订单,共I张订单。m表示BIN的序号,m与BIN的编号(j,k)对应关系如式(7)所示。矩阵元素 sim值1表示m所对应的BIN的波长和亮度符合订单i的需求,0表示不符合。
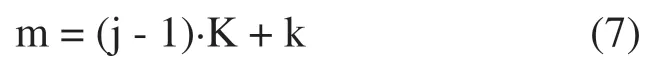
步骤2:个体编码。粒子个体采用整数编码,每个粒子表示所有订单的各BIN出货组合。假设LED厂有I张订单须满足,J个亮度等级和K种波段等级,则每个粒子的长度为I×J×K(即式(6)中转换矩阵的元素个数)。由于编码太长,不仅浪费大量的存储空间,而且降低运行效率。分析式(6)的转换矩阵,属稀疏矩阵。为了解除其稀疏特性,本文仅对矩阵中值为1的元素进行编码,不仅有效减少个体长度,降低了算法计算过程的复杂度,在一定程度上也提高了算法性能。
步骤3:确定参数值。根据数据规模和分布特征确定混合粒子群算法的控制参数,如种群个体数目N、最大进化代数G和变异概率P。由于该模型决策变量和限制条件都较多,为保证求解效果,因此种群个体数目N和最大进化代数G须设得较大。
步骤4:粒子初始化。产生初始种群时,通过在变量范围内随机生成正整数方式。各变量最小值根据式(4)定为β×iq,最大值根据式(3)定为qi。
步骤6:适应度值计算。粒子适应度值表示订单分配量。在本文中由于引入转换矩阵S将三维决策变量转换为二维,适应度函数因此表示为:
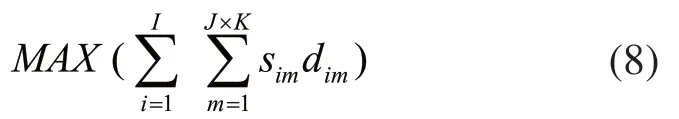
根据式(8)计算适应度值,得到个体最优粒子及群体最优粒子。
步骤7:交叉操作。交叉操作分为个体最优交叉和群体最优交叉。随机选定两个交叉位置,将个体分别和个体最优粒子及群体最优粒子进行交叉。
步骤8:变异操作。按变异概率P执行变异操作,生成新的个体。
步骤9:判断算法是否结束。判断是否达到最大进化代数G,如果未达到,则转步骤5,否则执行以下步骤。
步骤10:群体最优粒子即为最佳解。
4 算例
为了验证本研究提出的方法的有效性和优越性,本文针对具体的一家LED芯片厂的订单分配进行优化,求解各BIN的最佳出货组合。假设该LED厂将芯片按波长分为3种波段,按亮度分为3个等级,各BIN期初存货如表1所示。已知8张订单需要分配,各需求量与规格如表2所示。设定β 值为2%,也就是每个符合产品规格的BIN最小出货量为其订单需求的2%,小数点部份无条件进位。具体优化步骤如下。
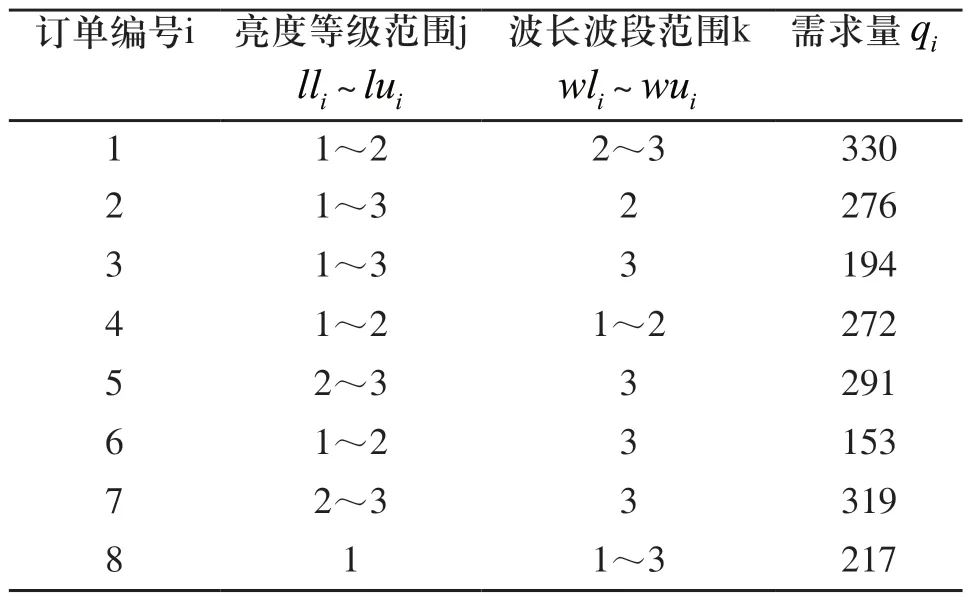
表2 各订单需求规格范围及数量
首先根据已知条件生成转换矩阵S,共8行9列,如式(9)所示。

接着构建用于优化的适应度函数如式(10)~式(13)所示。
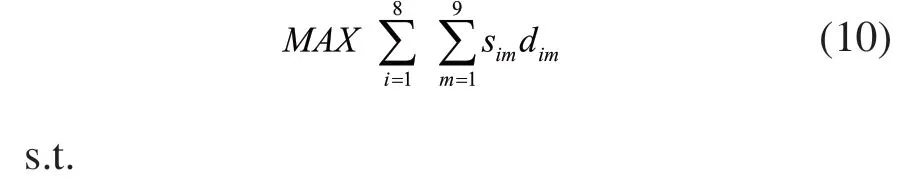
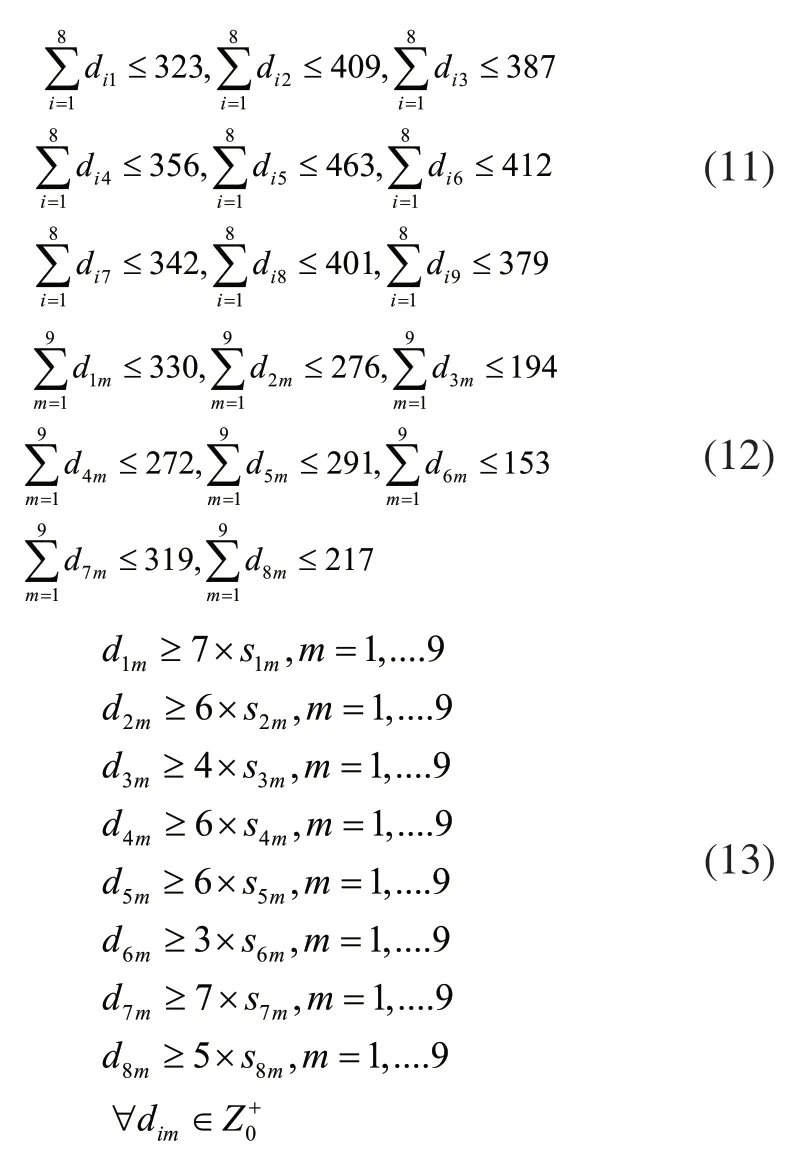
最后使用本文提出的混合粒子群算法进行求解,经400次进化后,得到群体最优粒子为[1769138795617515238415718237413515610746163156166546],转换为二维矩阵D(共8行9列),如式(14)所示。算法进化过程如图1所示。由式(10)得到此时的订单分配总量为2052,即所有的订单需求均得到满足。式(14)中每一行的和即为各订单的分配量(也就是330,276,194,272,291,153,319,217),每一列的和即为该列号所对应的BIN的总出库量(也就是323,294,314,23,218,389,0,175,316),各BIN期末库存如表3所示。从式(14)和表3可以看出,符合订单1的BIN有4个,分别对应表3中的编号为(1,2),(1,3),(2,2),(2,3)的BIN,其出货量分别为176,9,138,7。满足订单2的BIN有3个,分别对应表3中的编号为(1,2),(2,2),(3,2)的BIN,其出货量分别为95,6,175,依此类推。

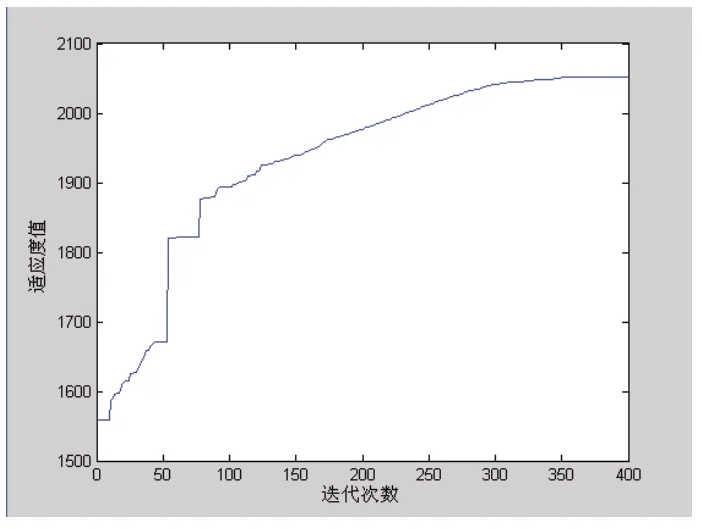
图1 混合粒子群算法的进化过程
5 结论
LED芯片厂为LED产业很重要的一环。LED厂一般将芯片按亮度和波长用不同的BIN来分类。客户下单时的产品需求规格以亮度等级范围和波长波段范围表示,因此合乎规格的BIN有多种。要满足一张订单,有无限种BIN出货数量组合可满足。为了让尽量多的订单可出货,如何优化各订单的BIN库存分配组合,是一个必须解决的重要问题。本研究提出一种混合粒子群算法来决定各订单的最佳BIN库存分配组合,以实现出货数量最大的目标。实证结果充分证明了该方法的有效性。本研究提出的方法在现实的LED厂中具有良好的经济效益和广阔的应用前景,不仅最大限度地满足了订单需求,提高了客户的满意度,而且有效降低总体库存水平,减少生产资金占用,提高企业的经济效益和市场竞争能力。
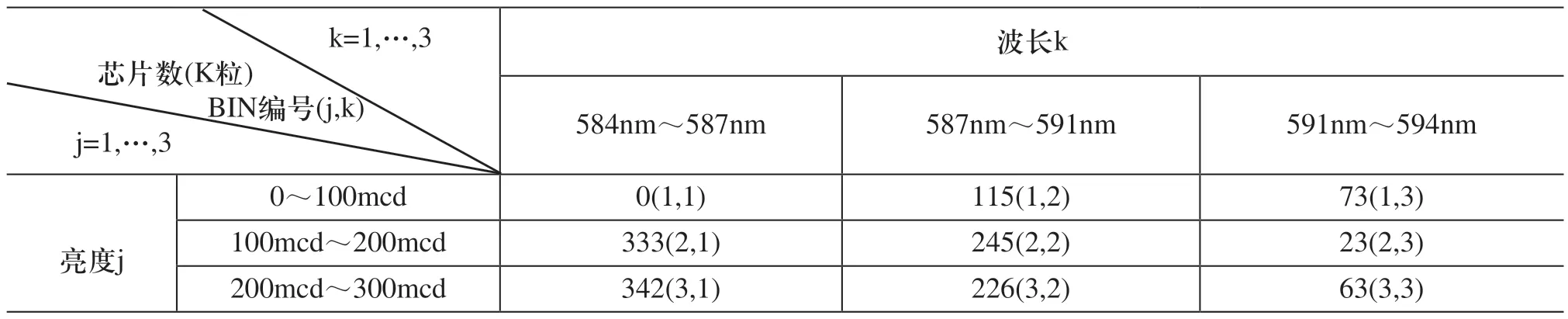
表3 三种波段和三种亮度等级的LED芯片厂各BIN期末库存
[1]Wu HH,Li MF,Hsu TF.An order fulfillment model for the LED chip manufacturing plant[J].Adv Mater Res,2013,694-697:3446-3452.
[2]Wu HH,Li MF.A study of the order fulfillment and production model for the LED die manufacturer[A].In:Proceeding of Chinese Institute of Industrial Engineers Confrence[C].Hsinchu,Taiwan,2011,55-61.
[3]Chang MH,Das D,Varde PV,Pecht M.Light emmiting diodes reliability review[J].Microelectron Reliab,2012,52(5):762-782.
[4]Scholand MJ,Dillon HE.Life-Cycle assessment of energy and environmental impacts of LED lighting products -Part 2:LED manufacturing and performance[J].Pacific Northwest National Laboratory and the U.S.Department of Energy,2012.
[5]Wu HH,Li MF,Yeh CH.A study of the material reissued models for an insufficient output of the LED chip manufacturing plant[J].Adv Mater Res,2013,694-697:3434-3440.
[6]Wu HH,Wu HH,Li MF.A study of the shifting MO model for an insufficient output of the LED die manufacturing plant[A].In:Global Business &International Management Conference at NYIT-Vancouver Campus[C].Canada,2013,6(2):46-55.
[7]Wu HH,Yeh CS.A study of the bin inventory allocation model for LED-CM plants[J].In:2nd International Conference on Materials and Manufacturing Research,Dalian,China,2014,85-89.
[8]Ayough A,Zandieh M,Farsijani H..GA and ICA approaches to job rotation scheduling problem:considering employee's boredom[J].Int J Adv Manuf Technol,2012,60:651-666.
[9]Yeniay O.Penalty function methods for constrained optimization with genetic algorithms[J].Math Comput Appl,2005,10(1):45-56.
[10]Chen WC,Liu KP,Liu BH,Lai TT.Optimization of optical design for developing a LED lens module[J].Neural Comput &Applic,2013,22(3):811-823.
[11]蒋大奎,李波,潭佳音.一类求解订单分配和排序问题的集成优化算法[J].控制与决策,2013,28(2):217-222.
[12]Lin YC,Wang KS,WANG FS.A mixed-coding scheme of evolutionary algorithms to solve mixed-integer nonlinear programming problems[J].Comput Math Appl,2004,47(8-9):1295-1307.
[13]颜俊华,张敏,王永军.基于遗传算法的智能粒子群优化方法[J].西南大学学报(自然科学版),2010,32(11):135-139.
[14]Chuang SP,Hsu TS,Yang CL.Parallel work center scheduling with release dates,due dates,and resourcedependent processing times[J].Int J Adv Manuf Technol,2009,40:193-202.
[15]Jiang XY,Wu HH.Optimization of setup frequency for TOC supply chain replenishment system with capacity constraints[J].Neural Comput &Applic,2013,23(6):1831-1838.
