径向永磁调速器磁极布置对电磁场及转矩的影响研究
2014-12-18孙建军
杨 帆,孙建军
(天津工业大学 机械工程学院,天津 300387)
0 引言
能源是人类活动的物质基础,人类社会的发展离不开先进能源技术的使用。在当今社会,由于能源利用率低,环境污染严重,节能减排成为全世界共同关注的重要问题。现如今许多泵类、风机类负载都采用机械节流方式调节流量和风量[1],这种落后的调节方式使得设备长期低负荷运转,如果对泵类、风机类负载使用调速控制,不仅能够达到节能减排的目的,而且能够保证产品质量,满足生产工艺要求。现今调速技术很多,调速市场上主要以变频调速居多。但是由于变频调速器的使用环境要求较为严苛,在高温、潮湿、冲击负载、易燃易爆等恶劣环境下使用有一定的局限性。而径向永磁调速器对环境适应性良好,可以在上述恶劣环境中使用。径向永磁调速器通过调节永磁体转子与导体转子之间的啮合面积来进行调速,实现了电机与负载的无机械连接的传动方式,减小了机械振动,同时节能效果显著,节电率可达20%~66%。本文采用ANSYS仿真分析软件对径向永磁调速器的电磁场进行分析研究,得出了不同的磁极布置对其电磁场和输出转矩的影响,为径向永磁调速器的优化设计提供了理论依据。
1 径向永磁调速器的电磁场理论分析
径向永磁调速器主要由钕铁硼永磁体转子、铜导体转子以及调节器三大部分组成,如图1所示。当铜导体转子在电机的驱动下做切割磁力线运动时会产生涡流,同时涡流产生的感应磁场与永磁场相互作用,从而带动负载运动。径向永磁调速器通过调节铜导体转子与永磁体转子之间的啮合面积(即调节永磁体转子轴的轴向伸出长度)就可以改变负载上的输出转矩,从而获得可控制,可调整的负载转速。

图1 径向永磁调速器结构示意图
当径向永磁调速器处于工作状态时,铜导体转子在永磁体激发的磁场中做切割磁力线运动进而产生涡流,而产生的涡流大小与分布在铜导体上的磁感应强度有着直接关系。由于永磁体采用径向充磁方式,且磁场方向随着铜转子的旋转角度一同变化,所以在铜转子上会产生一个沿Z轴方向的电流,电流产生的电动势为EZ,根据电磁场基本理论,即有铜导体所受到的磁感应强度为[2]。

式中,BZ为工作时气隙磁场处的磁感应强度;
P为磁极对数;
θ为转子的旋转角度。
对式(1)求偏导,并带入法拉第电磁感应定律:

对上式两边进行积分可得:

根据洛伦兹方程中运动导体产生的涡流密度和磁感应强度的关系:

式中:E为运动导体产生的电动势;
V为导体运动的速度;
B为导体受到的磁感应强度。
将式(4)带入上式可得铜导体上的涡流密度为:
通过分析铜导体上的磁感应强度与其表面产生的涡流两者之间的关系可以得出,当永磁体磁极对数,导体转速一定的条件下,铜导体表面产生的涡流密度与铜导体所受到的磁感应强度成正比,随着磁感应强度值的增大,铜导体表面产生的涡流也越大,涡流所激发的感应磁场随之变大,当永磁场与之作用时,使得永磁转子的输出转矩也增大。
2 径向永磁调速器的有限元模型建立
对径向永磁调速器的电磁场进行仿真分析,以验证理论分析的正确性,同时分析出不同磁极布置对径向永磁调速器的磁场及输出转矩的影响。采用ANSYS有限元分析软件可以对二维、三维电磁场进行模拟仿真,虽然分析的径向永磁调速器是三维问题,但由于其结构的对称性,可以将三维问题有效的简化为二维问题解决,这样可以缩短分析计算的时间,又能真实的反映涡流和磁感应强度的分布规律。
对不同磁极布置的径向永磁调速器的涡流和磁感应强度的分布进行仿真分析。步骤如下:1)几何模型的建立。在本文中,考虑永磁调速器结构的对称性,选取12对瓦形永磁体结构进行研究,采用几何模型的1/4进行有限元分析,如图2所示。2)选取单元类型及定义材料模型参数:由于PLANE53单元常用于电磁混合场的二维瞬态分析,故直接选用PLANE53单元[3]。需定义的材料属性有:铜的磁导率为1.0H/m,电阻率为1.75×10-8Ω·m,空气的磁导率为1.0H/m,铸铁的磁导率为200H/m,钕铁硼永磁体磁导率为1.2H/m(假设其退磁曲线为线性),同时定义永磁体的磁矫顽力矢量,通过改变其值的正负可以定义永磁体的N-S极朝向。由于分析的是瞬态电磁场,固还需要定义一个速度效应常数说明铜转子的转速。3)网格划分:为尽量提高计算精度,文中选择4级精度划分,生成的网格结果如图2所示。4)模型边界条件的施加和参数的求解:假设模型边缘边界无磁漏,则磁通量与边界平行,需要施加模型的平行边界条件[3]。在求解时首先定义分析类型,由于求解的是永磁调速器的二维瞬态电磁场,固选用命令“Transient”进行电磁场分析,然后定义载荷步选项,最终利用POST26处理器查看径向永磁调速器的涡流分布及相关的电磁场参数值。

图2 二维仿真模型及网格划分
3 不同磁极布置的径向永磁调速器的瞬态电磁场仿真结果
永磁调速器磁体转子中的磁极排列多采用N-S异极排列[4],本文通过改变磁极在永磁转子中的分布情况(即采用N-N或S-S同极排列),利用ANSYS仿真软件分析并比较这两种不同排列方式下的涡流及其磁感应强度的分布情况,并且计算出磁感应强度值的大小,从而验证理论分析结果的正确性,为径向永磁调速器的进一步研究提供基础数据[5]。

图3 异极排列磁极的磁感应强度分布
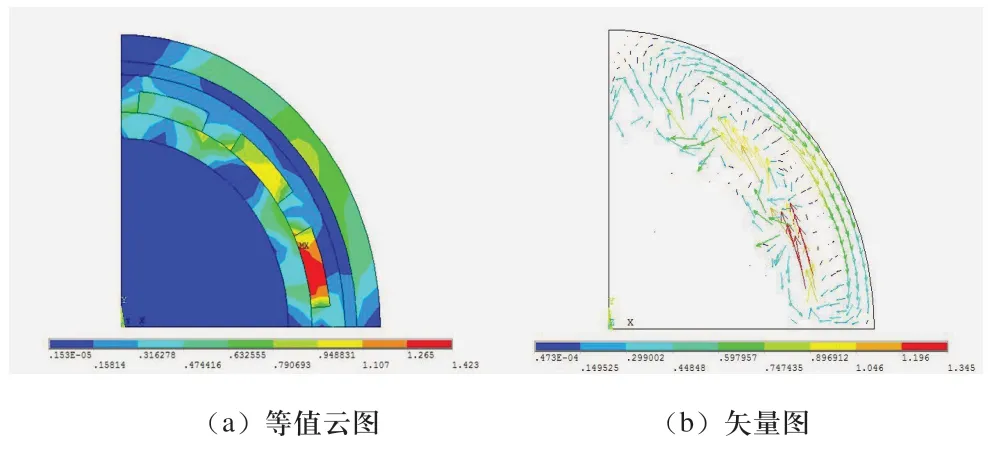
图4 同极排列磁极的磁感应强度分布
图3、图4分别为输出轴转速为1000r/min时两种磁极排列对应的磁感应强度分布图。由图可知,同极排列磁极比异极排列磁极所产生的磁感应强度的分布范围更广,但作用在铜导体的范围较小,后者的磁感应强度值大于前者。由于当磁场作用的有效截面积一定时,磁场作用到铜转子上的磁通量只与磁感应强度有关,磁感应强度值越大,则磁通量越大[6]。当永磁调速器处于工作状态时,铜转子上的涡流大小与磁通量有着直接关系,磁通量越大,产生的涡流也越大[7],从而涡流感应出的感应磁场就越大,当永磁场与之相互作用时,就使得永磁转子输出的转矩也随之变大。所以,作用在铜导体上的磁感应强度值的大小直接关系到铜导体上产生的涡流大小。

图5 径向永磁调速器涡流分布
输出轴转速为1000r/min时磁体异极排列与同极排列产生的涡流分布情况如图5所示,在相同的转速下,异极排列磁极在铜导体上产生的涡流大于同极排列产生的涡流,这就使涡流感应出的感应磁场增大,从而使永磁场与之作用的能力增强,最终使输出转矩得到明显提高。
4 径向永磁调速器的转矩/转差测试实验
本文采用实验的方法测试出在同一啮合面积下按照不同磁极排列的驱动侧与负载侧的相对转速(即转差)与转矩之间的关系。根据实验目的搭建的实验平台主要包含了变频器,驱动电机,径向永磁调速器,转矩/转速传感器,磁粉制动器和直流电源相当于模拟负载,搭建的实验测试平台如图6所示。

图6 转矩测试实验平台
在转矩测试实验中,首先要保证铜导体与永磁体之间的啮合面积为定值,然后用变频器调节电机转速,使铜导体驱动侧转速达到预先设定的1000r/min,然后调节直流电源使磁粉制动器逐渐加载(即逐渐增大转差),当模拟负载侧转速每次下降50r/min时,记录下此时的转矩值。然后改变磁极排列方式,按照上述实验过程重复操作,从而得出在啮合面积一定的条件下不同磁极排列方式的转差与转矩之间的关系曲线如图7所示。
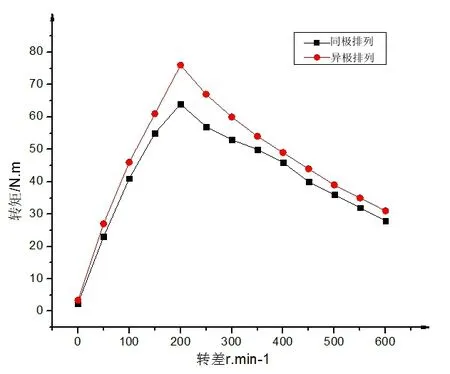
图7 永磁体轴伸出5mm时异极排列和同极排列的转差与转矩的关系曲线
通过多次对比实验,在此以永磁体轴伸出长度为5mm说明实验结果。在保证同一啮合面积条件下,按照异极排列的径向永磁调速器的最大转矩值为58.26N·m,而按照同极排列的只有53.82N·m,此时按照不同排列方式的转矩差也达到最大值。随着转差的逐渐增大,异极排列的输出转矩仍大于同极排列的输出转矩,但转矩差值逐渐减小并趋于平稳,由此可见按照异极排列的径向永磁调速器磁场利用率更高,输出的转矩更大。
5 结论
1)利用ANSYS有限元仿真分析软件对径向永磁调速器进行瞬态电磁场分析,验证了理论分析结果的准确性,得出了按照异极磁体排列的径向永磁调速器作用在铜导体上的磁感应强度更大,产生的涡流越多。
2)采用实验的方法得到径向永磁调速器在不同磁极排列方式下的转差与转矩之间的关系,从而分析出不同的磁极布置对径向永磁调速器输出转矩的影响,进一步验证了在啮合面积一定的条件下按照异极磁体排列的径向永磁调速器输出的转矩更大,所以对工作磁场利用率有明显优势。这就为下一步对径向永磁调速器的优化改进提供了良好的依据。
[1]钱广华.永磁调速器应用在鼓风机上的节能效果分析[J].电气节能,2009,28(22):24-27.
[2]牛晓博.基于 ANSYS 的永磁调速器磁场研究:(硕士学位论文).吉林:吉林大学,2012.
[3]张倩,胡仁喜,康士廷.ANSYS12.0 电磁学有限元分析从入门到精通[M].北京:机械工业出版社,2010.2:2-3.
[4]王旭,王大志.永磁调速器磁路结构设计.电气传动,2011,9(10):55-58.
[5]赵克中.磁力驱动技术与设备.北京:化学工业出版社,2004.
[6]张宏刚.永磁耦合器损耗的计算与分析:(硕士学位论文).吉林:吉林大学,2008.
[7]张泽东.永磁磁力耦合器设计与关键技术研究:(硕士学位论文).沈阳:沈阳工业大学,2012.
