超大变形应变测量方法的研究

张 川， 郭 楠

（1.中国空空导弹研究院，河南 洛阳 471003；2.西安交通大学，陕西 西安 710049）

0 引 言

随着新型材料的不断研发以及航空工业对材料的可靠性、经济性、轻量性的要求，了解新型材料的基础力学性能，对航空飞行器结构设计起着重要的作用。飞行器在工作时会遇到极端恶劣环境和受到复杂应力，材料所表现的力学行为明显区别于常温实验状态。材料的变形行为是了解材料性能的基础，特别是新型材料在复杂环境下表现出的超大变形行为，有助于深入了解飞行器的断裂过程和破坏机制，能使新型材料提高安全性并得到广泛的应用。

目前对超大应变还没有有效的测量方法，传统的各种应变片因其自身的接触、单点、单向测量的缺陷，不能用于全场变形应变场的检测，并且存在非常有限的应变测量范围；激光干涉法其光路比较复杂，调节过程比较繁琐；数字散斑干涉法存在设备造价高、光路复杂、抗环境干扰能力差的缺陷；数字图像相关法近几年发展成熟，应用广泛，但对超大变形的研究比较少，由于超大变形的应变较大，图像匹配比较困难，因此国内外专家主要停留在用“分段”思想对超大变形进行应变测量[1-3]，这种方法积累了误差。本文提出一种通过优化数字图像相关法中固有算法的参数，直接利用灰度的相似函数对未变形图像和已变形图像进行比对的超大应变测量方法，避免了误差多次叠加，提高了测量应变精度。

1 数字图像相关方法测量超大应变原理

利用数字图像相关法[4-5]可以动态测量全场应变，首先对试件喷涂高对比度的散斑，用已标定的相机对发生变形的试件进行连续拍摄，得到一组连续图片；然后对未变形图片需测量应变区域划分网格区域，根据子区中灰度的相关性，在已变形图像中找到对应的变形子区；最后根据未变形与已变形子区中心点的变化，根据算法计算出这一点的应变，以此类推到整个变形区域。

针对超大变形应变的测量，其算法的基本原理也是判断相关性，利用变形后图像与未变形图像做比对，得到变形子区。但是，与传统算法不同的是：传统算法是根据变形的最后一张图像与未变形图像做比对，这种算法在小变形计算时具有很好的适应性，随着变形的增大，变形后图像与未变形图像之间的差别越来越大，其相关程度也越来越低，在寻找相关变形子区时计算量巨大，精度也大大降低，甚至出现错误匹配。鉴于此，本文提出一种跟踪算法，即在未变形图像中任取一个子区，以子区为目标，算出未变形子区其余子区中心点的位置；然后在图像序列的第一张变形图像，根据一般的相关性匹配原理，得到与未变形图像中选取子区相对应的变形子区，此时由于连续两张图像之间变形很小，因此相关性很高，应变计算精度相应很高；同样地，以变形区的第一个子区为目标，变形区其余子区根据相对应的未变形中其余子区中心点坐标很容易找到其大致变形位置，即粗匹配，再根据算法进行精确匹配；同样地，继续计算变形的第二张图像、第三张……，直到最后一张，计算选中子区时都是以前一张图像作为参考。所以，与传统方法相比，虽然都是根据相关性准则判断其相关性确定子区大小，但本文方法在选取子区时，利用选定子区跟踪的方法，可以更快更精确地找出与之对应的变形子区，算法稳定性更高。

1.1 选定子区的匹配原理

数字图像相关法的核心是对变形前后的相邻两幅图像的子区进行相关灰度匹配，根据相关准则函数确定目标的准确位置。如图1所示，P（x0，y0）为其中一个变形前选定子区的中心点，Q（xi，yj）为同一子区内任意一点，P′（x′，y′）、Q′（xi′，yj′）分别为子区变形后与P、Q的对应点，其中，xi=x+Δx，yj=y+Δy，x′=x+u，y′=y+ν。根据数字图像相关法的图像灰度级与物体表面呈一一对应的关系假设，变形前后P、Q灰度函数不变，即f（x0，y0）=f（x0+u，y0+ν），f（xi，yj）=f（xi+u′，yj+ν′），把位移函数u（x，y）、ν（x，y）在x0，y0处用泰勒多项式展开，略去二阶及以上的无穷小量，可得到Q′的坐标值，即x′=x0+Δx+u+uxdx+uydy，y′=y0+Δy+ν+νxdx+νydy；因此，通过小区域内的图像位移函数可以大致确定P′点和子区内任意点Q′的位置及物体表面的变形量。要精确获取子区变形量，需要通过一定的算法对子区内不连续点的亚像素灰度值进行插值计算，得到整体的灰度值，然后通过相关准则判断相关子区进行匹配，最后通过子区中心坐标值的变化，可计算出子区平面内应变。

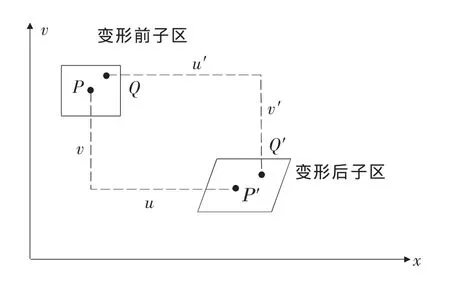
图1 数字图像相关法变形匹配示意图

1.2 相关准则函数

假设未变形子区中共有M个像素，且图像灰度受理想高斯白噪声影响，用最小距离平方和相关系数CSSD[6]来评价未变形子区和已变形子区的相似程度，通过算法求取相关系数的最小值，可以在变形图像中找到与未变形子区具有最大相似度的目标已变形子区，即：

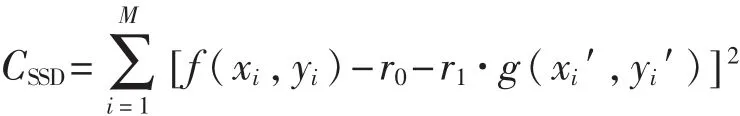
式中：f（xi，yi），g（xi′，yi′）——未变形子区和已变形子区中心点的灰度值；

r0，r1——用于补偿光照引起的灰度线性变化。

2 试验方法及结果

2.1 试验过程以及后处理

利用传统的数字图像法计算超大应变时，因不满足相关函数的迭代阀值，应变计算很快会断裂。目前，很多专家采用“分段”式，也就是在断裂处设置多个基准进行匹配，变形图像不再以一个基准匹配，造成了误差累积，也损失了精度。“分段”式是解决以牺牲精度为代价计算超大应变的有效方法。本文提出的跟踪选定子区法，以顺序前后两张图像相比对，可以很好地解决匹配问题，经过多个工程的多次试验发现，以同样的迭代阀值，仅仅调整后处理参数，就可以不必“分段”，一次性以一个基准进行匹配，得到全场超大应变值，虽然调整后处理参数不具有通用性，但针对特定的工程，可以大幅提高精度，在以后的工作中，针对不同工程，设置后处理参数的规律性是进一步研究的工作。因此，跟踪选定子区法与调整后处理参数相结合，有效解决了超大变形的应变计算问题。

试验采用Xjtudic系统在实验室常温环境下对标准塑料试件进行单向拉伸，拉伸速度为60mm/min，利用两个相机对拉伸过程进行连续拍摄，图片在后处理软件中进行应变计算。在后处理中，使用一般测量应变参数，如子区尺寸：15×15像素，步长 30×30像素，连续性阀值设为0.05，以未变形图像为基准等，匹配时变形图像就会发生与未变形图像相关性差，发生断裂，如图2所示左右相机的匹配断裂图像。

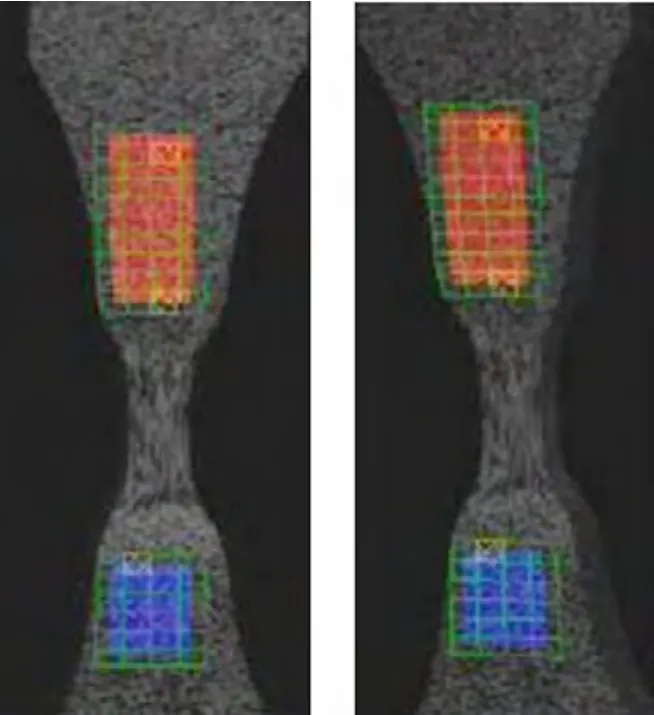
图2 应变子区断裂图像

根据本文提出的匹配及应变算法的原理，设置未变形图像为唯一基准，后续变形图像以唯一基准进行相关匹配。后处理参数优化为：子区尺寸10×10像素，步长16×16像素；迭代残差阀值所起的约束作用阻碍工程计算，由原来20设为200，避免更多正确匹配点被过滤；放大连续性阀值，由0.05设为1；调小应变窗口大小，使其由原来25个相邻面片变为9个面片来确定一个面片中心点应变；创建3个种子点（种子点算法适合大变形）。对于多个基准，测量应变大小时，计算模式和分析模式需要变换为以第一帧为参考，根据之前的面片断裂始发处，间隔设置参考基准，面片仍有空洞，可选择调小窗口完整率改善。经优化后的变形过程如图3所示，最大应变分别为135%、221%、398%、525%的图像。

2.2 结果分析

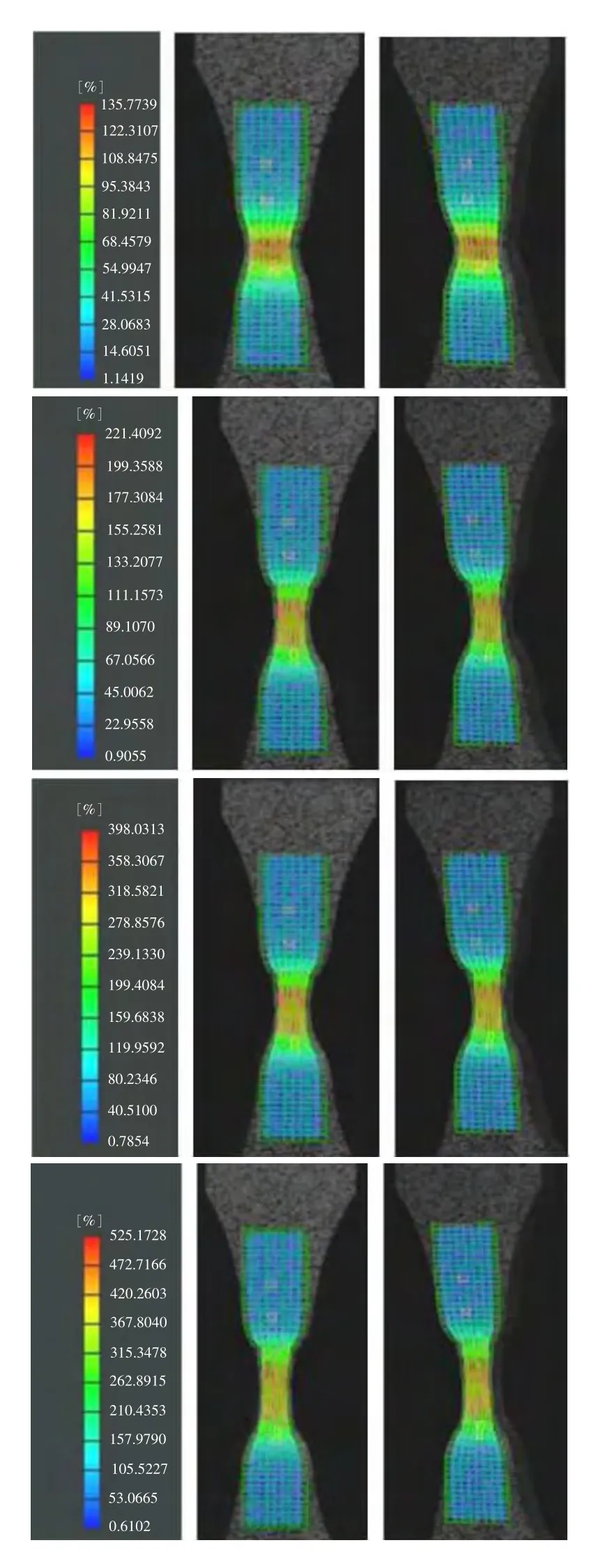
图3 最大应变分别为135%、221%、398%、525%的左右相机图像

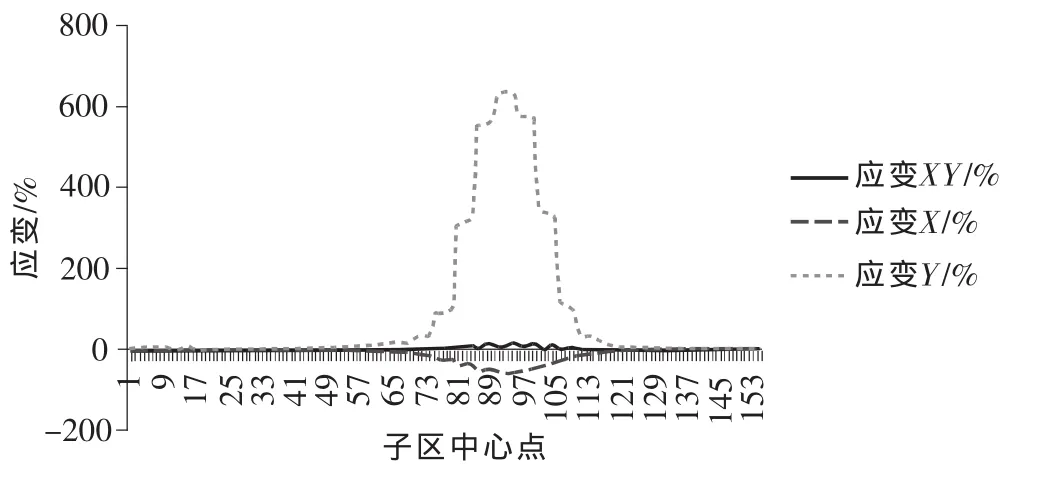
图4 试件断裂前的最大应变状态

塑料试件拉断前的应变场如图4所示。图中纵坐标表示应变，横坐标为每个子区中心点，排列顺序为从左上角起序号为1，以水平方向排序，一排共5个点，然后转到第二排左起第一个点，序号为6，共31排，以此类推到最右下角的点。可以看出最大应变发生在试件靠近中心位置，应变值超出600%，所需计算的应变区域中间位置应变变化较大，两端区域几乎不发生变形，根据相机像素大小和相机离试件的距离，可以计算出发生变形处的距离，台阶处表示试件横截面上的5个点，可以看出横截面处的应变以Y向中心对称分布。此结果为试件断裂前的应变数据，同样可以得到发生应变时的任意状态应变数据。

3 结束语

利用数字图像相关法可以非接触、全场地测量超大变形的应变状态，能够准确判断试件断裂位置和试件极限应变，不仅可以测量试件成形最终状态的应变，还能够有效测量试件所有变形过程中的任意状态表面应变分布，是一种测量超大变形应变的有效手段。

[1] 叶南，张丽艳.大变形下基于数字图像相关的改进分段位移传递法[J].光学学报，2010，30（4）：976-983.

[2] Tang Z Z， Liang J， Xiao Z Z， et al.Large deformation measurement scheme for 3D digital image correlation method[J].Optics and Lasers in Engineer，2012，51（2）：023602-023609.

[3] 唐正宗，梁晋，肖振中，等.大变形测量数字图像的种子点匹配方法[J].西安交通大学学报，2010，44（11）：51-55.

[4] Sutton M A，Cheng M，Peters W H，et al.Application ofan optimized digitalcorrelation method to planar deformation analysis[J].Image Vision Comput，1986，4（3）：143-150.

[5] Tang Z Z， Liang J， Xiao Z Z， et al.Three-dimensional digital image correlation system for deformation measurementin experimentalmechanics [J].Optical Engineering，2010（49）：103601.

[6] Pan B， Asundi A， Xie H.Digital image correlation using iterative least squares and pointwise least squares for displacement field and strain field measurements[J].Optics and Lasers in Engineering，2009，47（7-8）：865-874.