基于指数效用函数的保险基金投资决策及保费确定

王后春， 崔玉乐

（安徽建筑大学 数理学院，合肥 230601）

1 前 言

保险公司的投资状况与其经营效益及稳定性高度相关。事实上，保险投资己成为保险业经营收入的重要源泉。在发达国家，保险公司的保险投资收益远远高于其真接的承保收益。保险投资是现代保险业得以生存和发展的重要支柱，它不仅可以提高公司的竞争地位，还关系到国家的经济稳定。保险公司的偿付能力和效益最终取决于其投资收益。因此，为适应保险市场的发展，研究保险投资以及在此基础上的保险定价等问题已成为当前的一项重要课题。

随着保险公司运作限制的放宽，保险公司可同时开展包括证券、货币、保险等在内的多个市场的业务，保险公司在各市场的资产配置直接影响公司的收益与风险。有关保险公司的投资策略选择问题，已经引起了众多学者的关注。目前，该类问题主要集中在对不同的盈余过程和不同的目标函数下，利用随机控制理论中的动态规划方法寻找最优的投资策略和再保策略。如在保险公司盈余过程近似为扩散过程，风险资产价格服从几何布朗运动情形下，Browne（1995）研究了破产概率最小和期望终值效用最大这两种情况下保险公司的最优投资策略选择问题［1］。在经典的复合泊松风险模型下，就风险资产价格过程服从几何布朗运动的情形，Hipp ＆Plum（2000）在理赔分布服从指数分布情形下获得了破产概率最小化目标下的最 优 投 资 策略的 显 式 解［2］；Schmidli（2001，2002）研究了最优比例再保策略和投资策略的选择问题，证明了在破产概率最小时对应HJB方程解的存在性和最优性，但并没给出具体解的形式［3－4］。Yang ＆ Zhang（2005）考虑了保险公司的风险过程为跳跃扩散模型，保险公司允许资金投资于风险资产和无风险资产的情况下，在期望终值效用最大目标下给出了保险公司的最优投资策略，获得了破产概率最小时对应的HJB方程［5］。Wang（2007）讨论了未来某时刻使得保险公司责任准备金的指数效用最大化的最优投资策略［6］。国内学者刘洁等人（2013）通过对经典的复合泊松风险模型的连续扩散近似，利用动态规划原理分别得出了在破产概率最小和终值期望效用最大两种目标函数下，保险公司的最优投资和最优再保策略的显式解和对应的目标函数值，并对两种目标函数下的最优策略做了比较研究［7］。姚海祥等人（2013）在金融市场仅存在风险资产的情况下研究了投资终止时间不确定且带有通货膨胀影响的最优投资组合选择问题［8］。

纵观现有关于保险投资策略的文献，没有考虑保险公司在承保期的期初一次性收取保费这一现实情况，也没有考虑保费确定即保险定价问题。不同于姚海祥等人（2013）、刘洁等人（2013）、Wang（2007）提出的保险公司以常数保费率连续收取保费的情形，本文拟假定保险公司在一个承保周期的期初一次性收取保费，且假定保险公司盈余全部投资于一类风险资产（股票）和一类无风险资产（债券），风险资产价格服从几何布朗运动，索赔总量服从复合泊松过程。就这种跳跃扩散风险模型的情形，本文采用指数效用函数，在期望终期财富指数效用最大化目标下，利用随机控制原理，通过求解HJB方程，获得最优投资策略的解析形式。根据相应的目标函数值，在保险公司是风险中性的假设下，给出期初趸缴保费计算公式。

2 跳跃扩散风险模型

首先建立投资影响下保险公司盈余过程的数学模型。

设本文所涉及的随机变量和随机过程都定义在完备化的概率空间（Ω，F，P）上。

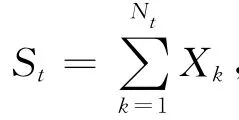
考虑一个仅有两类资产的金融市场，其中一类是无风险资产，另一类是风险资产。假定风险资产的价格过程｛Lt，0≤t≤T｝满足

其中Wt是标准布朗运动，μ，σ均为正常数，分别表示风险资产的期望收益率和收益波动率。

饭店的发展离不开有专业知识的人才，酒店的经营理念从过去的“顾客第一、顾客是上帝”转变为“顾客第一，员工第一”，万豪酒店集团早就提出“没有满意的员工就没有满意的顾客”，要关注员工，要让员工满意，在酒店工作有种归属感，保障员工的福利，这样才有充分挖掘员工的潜能，在员工实现自身的人生价值的同时，为酒店做出更大的贡献。

记保险公司在时刻t的盈余为Ut。为增加收益，保险公司计划对时刻t的盈余Ut进行两类投资:投资于风险资产的资金为πt，投资于无风险资产的资金为Ut－πt。则保险公司的盈余过程｛Ut，0≤t≤T｝满足

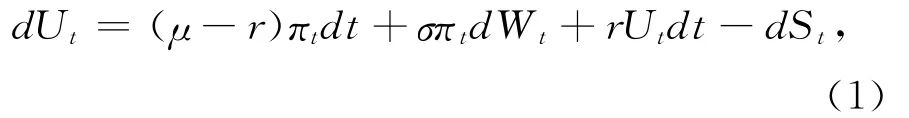
其中r≥0表示无风险利率。

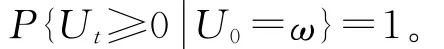
3 最优投资策略及保费公式

下面的研究不考虑交易费、税收和红利。

考虑到现实中大部分投资者为风险厌恶型投资者，本文采用指数效用函数u（v）＝－e－qv作为保险公司的效用函数，其中正常数q称为风险厌恶因子。

在跳跃扩散风险模型（1）下，保险公司希望通过最优投资策略π＊t来追求期望终期财富指数效用最大化。为此，定义索赔总量过程｛St，0≤t≤T｝下的值函数

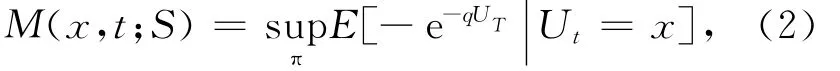
值函数M（x，t；S）表示t时刻保险公司的盈余为x条件下保险公司期望终期财富指数效用的最大值。

定理 在跳跃扩散风险模型（1）下，设值函数M（x，t；S）关于t一次可微，关于x二次可微。若t时刻保险公司的盈余为x，则期望终期财富指数效用最大化目标下保险公司最优投资策略为

结合（2）和（5），由伊藤公式及动态规划原理得值函数M（˜x，t）满足如下HJB方程

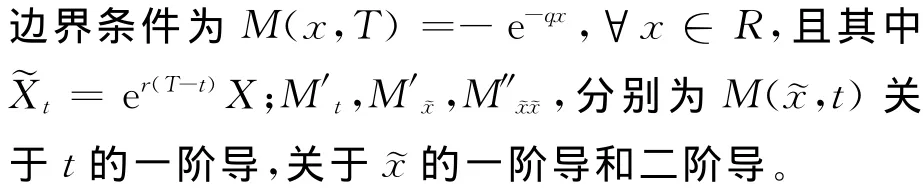
为解该倒向随机微分方程，猜测它有形如M（˜x，t）＝－e－q˜xf（t）的解，代入（6）得

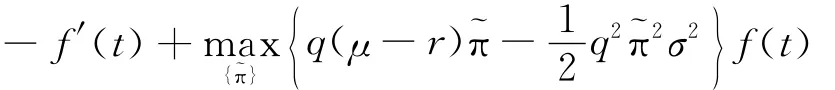
解一阶微分方程（8）并注意到边界条件f（T）＝1得

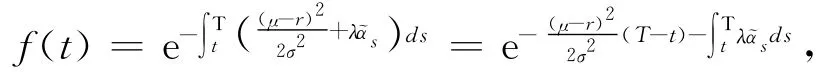
结合M（˜x，t）＝－e－q˜xf（t）知（4）成立。

在保险公司是风险中性的假设下，期初趸缴保费H满足

即在初始时刻不收取任何保费也不承担任何赔付责任与收取保费H因而承担赔付责任这两种情况下相应的最优值函数相等。

由（4）得

由（9），（10），（11）得期初趸缴保费为

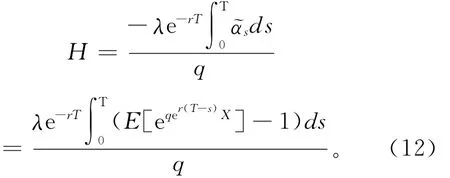
注1．从式（3）可看出，分配于风险资产的投资量随着其收益波动率σ的增大而减小，随着其期望收益率μ的增大而增大，随着保险公司风险厌恶因子q的增大而减小，随着无风险利率r的增大而减小。同时，最优投资策略对于无风险利率非常敏感，一旦利率调整，保险公司的最优投资策略就会作较大的调整。

注2．在保险公司是风险中性的假设下，期初趸缴保费H独立于初始盈余ω以及μ，σ，且是一个投资期［0，T］内索赔总量的确定性等价值的折现值。

在式（12）中，令r＝0得H＝h，故H是保险公司在无任何投资情况下的期初趸缴保费h的推广。

4 结束语

本文打破保险公司以常数保费率连续收取保费的局限，研究保费在一个承保周期的期初趸缴时，公司的盈余过程为跳跃扩散风险模型的情形下保险人的最优投资策略选择及保费确定问题。运用最优控制原理得到了保险公司的最优投资策略和最大化期望终期财富指数效用的解析表达式，同时对最优投资策略和有关参数的关系进行了简单分析。在此基础上给出风险中性假设下保险公司期初趸缴保费的计算公式。本文对保险人的投资运作及保险定价具有指导作用。

进一步，本文保费的计算方法也可以应用到责任准备金的计算。此外，本文模型还可以在其它一些方面进行拓展，如保险公司以变量保费率连续收取保费，以及分期收取保费等情形，今后将深入研究。

1 Browne S．Optimal investment policies for a firm with random risk process:Exponential utility and minimizing the probability of ruin［J］．Mathematics of Operations Research，1995，20（4）:937－958．

2 Hipp C，Plum M．Optimal investment for insurers［J］．Insurance:Mathematics and Economics，2000，27（2）:215－228．

3 Schmidli H．Optimal proportional reinsurance policies in a dynamic setting［J］．Scandinavian Actuarial Journal，2001，（1）:55－68．

4 Schmidli H．On minimizing the ruin probability by investment and reinsurance［J］．The Annals of Applied Probability，2002，12（3）:890－907．

5 Yang H，Zhang L．Optimal investment for insurer with jump－diffusion risk process［J］．Insurance:Mathematics and Economics，2005，37（3）:616－633．

6 Wang N．Optimal investment for an insurer with exponential utility preference［J］．Insurance:Mathematics and Economics，2007，40（1）:77－84．

7 刘 洁，赵秀兰．保险公司的最优投资和再保险策略［J］．模糊系统与数学，2013，2（3）:160－168．

8 姚海祥，伍慧玲，曾 燕．不确定终止时间和通货膨胀影响下风险资产的最优投资策略［J］．系统工程理论与实践，2013，33（1）:1－11．

9 林元烈．应用随机过程［M］．北京:清华大学出版社，2002．