非紧拓扑压函数的性质

王 威， 陈明朋

（1．应天职业技术学院 基础部，江苏 南京 210023；2．南京师范大学 数学科学学院，江苏 南京 210023）

1 引 言

在动力系统领域中，一个重要的课题是研究与系统复杂性有关的问题。熵和拓扑压是反映系统复杂性的重要概念。二十世纪Bowen，Pesin［1］人将熵的概念拓展到非紧空间。Faloner［2］在混合排斥子上建立了次可加的变分原理。Barreira［3］在紧致空间中建立了任意非可加的变分原理。之后它成为拓扑动力系统研究中的热点和难点问题。进入二十一世纪，在非紧空间上拓扑压的 工 作 成 为 热 点 问 题。Cao［4～6］，Feng［7］，Climenhage［8］，Mummert［9］得到了很多有价值的结论，并建立了非紧致集合上的变分原理。

设M（X）是X上所有的Borel概率测度集。M（X，T）⊆M（T）是所有T－不变的概率测度集。设Z⊆X为T－不变集。E（X，T）⊆M（X，T）为遍历测度集，且满足μ（Z）＝1，∀μ∈E（X，T），对于x∈X，定义概率测度

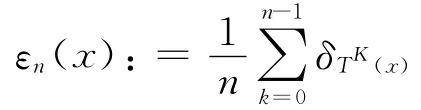
εn（x）的极限点集用V（x）表示，则V（x）⊂M（X，T）。

非紧集合的拓扑压的变分原理:若V（x）∩E（Z，T）≠φ，∀x∈Z，则对任意实值连续函数φ:

若φ＝0，即为非紧集的拓扑熵的变分原理。若Z为紧致集合，则与经典变分原理一致。2010年丰德军和黄文［7］定义了极限次可加函数并且给出了极限次可加函数序列下熵的变分原理。

2 本文需要用到的定义

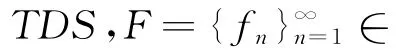
3 本文的主要结果

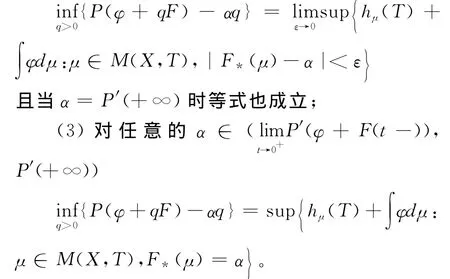
4 几个引理

5 定理3．1证明

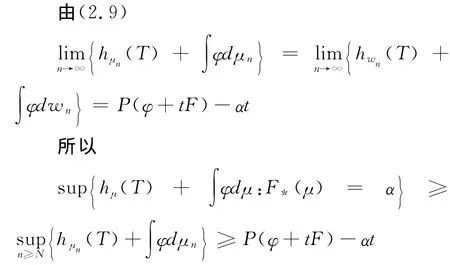
从而（3）得证。至此定理3．1得证。

1 Y．Pesin，B．Pitskel，Topological pressure and thevariational principle foe noncompact sets，｛Funktsional．Anal．I Prilozhen｝，1984 （4）:50－63 （in Russian）．

2 K．J．Falconer，A subadditive thermodynamic formalism for mixing repellers，J．Phys．A．1988（21）:L737－L742．

3 L．Barreira，A non－additive thermodynamic formalism and applications to dimension theory of hyperbolic dynamical systems，Ergodic Theory Dynam，1996（16）:871－927．

4 Y．Cao，D．Feng，W．Huang．The thermodynamic formalism for sub－additive potentials，Discrete Contin．Dyn．Syst．，2008（20）:639－657．

5 Y．Zhao and Y．Cao，Measure－theoretic pressure for subadditive potentials，Nonlinear analysis，2009（70）:2237－2247．

6 W．Cheng，Y．Zhao and Y．Cao，Pressures for asymptotically subadditive potentials under a mistake function，Discrete Contin．Dynam．Syst．Ser．A，2012（32）:487－497．

7 D．J．Feng，W．Huang，Lyapunov spectrum of asymptoticallysub－additive potentials．Commun．Math．Phy，2010（297）:1－43．

8 V．Climenhage，Bowen’s equation in the non－uniform setting，Ergodic Theory and Dynamical Systems，2011（31）:1163－1182．

9 A．Mummert，Thermodynamic formalism for almostadditive sequences，discrte contin．dyn．syst．2006（16）:435－454．