基于曲线拟合和网络拓扑的综合地图匹配算法＊

毕 军 朱 颖 程 勇

（1.北京交通大学城市交通复杂系统理论与技术教育部重点实验室 北京 100044；2.北京交通大学北京城市交通协同创新中心 北京 100044；3.山东济宁市鸿翔公路勘察设计研究院 山东 济宁 272000）

0 引言

现今的大多数车辆导航系统都采用全球定位系统（global position system，GPS）和航位推算法（dead reckoning，DR）来进行定位。但是，定位传感器都会存在着一定的误差，使得车辆定位位置与其真实位置不一致［1］。因此，研究如何快速、准确的减少这种误差，可以使车辆导航系统更好的为人们服务［2］。地图匹配是指载体上的GPS接收机采集载体当前的有关位置信息后，并从电子地图数据库中获取相关的道路信息，再将得到的载体的位置、速度、方向等信息，通过匹配算法对其进行实时修正，从而显示车辆在电子地图的准确位置的1种方法［3］。现有的地图匹配算法主要有基于权重、基于相关性、基于概率统计、基于曲线拟合，基于网络拓扑关系等匹配算法［4－5］。其中基于曲线拟合的匹配算法具有较强的稳定性，匹配精度高，但是对比较靠近的平行路段进行匹配时，该算法容易出错；基于网络拓扑的地图匹配算法会受到空间拓扑关系质量的影响，空间拓扑越大，匹配效果也就越差，应和其他的匹配算法结合使用。也有采用模糊逻辑、卡尔曼滤波等方法的匹配算法，这些算法虽然匹配精度高，但实现较为复杂［6－7］。笔者提出1种基于曲线拟合和网络拓扑的综合地图匹配算法，可有效解决曲线拟合算法的缺陷。

1 基本地图匹配算法的介绍

1.1 基于曲线拟合的地图匹配算法

在很多情况下，由于测试点分散，所求的曲线无法通过所有的测试点，因此需要1条反映测试点趋势的平滑曲线来近似测试结果，这就是曲线拟合［8］。基于曲线拟合的地图匹配算法以曲线拟合的原理为基础，通过对若干个原始定位数据的累加，经过曲线拟合计算，得出由这几个原始数据所确定的拟合直线的斜率。预先设定1 个门限值，在计算拟合直线斜率与各匹配候选路段斜率之间的差值之后，将各差值与门限值比较，取得低于门限值并且是所有差值中最小的1个差值，则对应这个最小差值的候选路段就是当前的匹配路段［9］。

曲线拟合算法的原理如图1，假设点1，2，3是已匹配点，点4是待匹配点，由图可知拟合直线与路段1夹角较小，故点4 被匹配到路段1。由于基于曲线拟合的地图匹配算法不是单个测试点独立匹配，而是考虑了车辆轨迹的连续性，使得此算法具有较强的稳定性，对于交叉点的匹配问题也能很好地解决。

1.2 基于网络拓扑的地图匹配算法

使用路段连通性或路段的几何形状的地图匹配算法是基于网络拓扑的地图匹配算法。它通过对前1次匹配结果和车辆前进方向的分析，利用道路层的空间网络拓扑关系，确定当前GPS定位点的候选路段的范围，并计算出当前GPS定位点的匹配点。该算法的依据是：车速有限，在一定时间范围内，车辆只能行驶在与上一匹配路段相连的道路上，不可能在其他路段［10］。

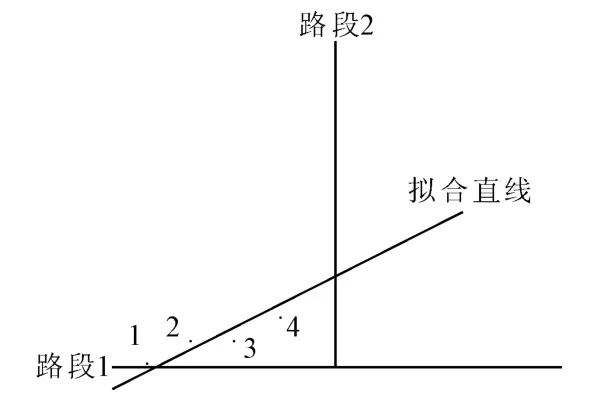
图1 曲线拟合原理图Fig.1 Principle diagram of curve fitting

2 综合地图匹配算法的实现

基于曲线拟合的地图匹配算法充分利用了GPS历史数据，使得该算法在匹配路段的选择方面具有较强的稳定性，但是它只考虑了拟合直线与候选路段的斜率，以及定位点与候选路段的距离关系，对于相互靠近的平行路段则无法准确辨别，所以对于这类路段，仅仅依靠曲线拟合算法会造成匹配错误。网络拓扑反映的是道路之间的连通关系，在一定时间范围内，车辆只能行驶在与上一匹配路段相连的道路上，而平行路段中只可能有1条（即匹配路段）是与上一匹配路段相连的，因此，利用网络拓扑关系可以排除平行路段的干扰。本文的地图匹配算法基于曲线拟合并结合路网拓扑关系，不但能弥补基于曲线拟合的地图匹配算法在距离较近的平行路段匹配率不佳的缺点，还能有效缩小候选路段的搜索范围，减小算法复杂度。

2.1 数据预处理

城市道路路况复杂，隧道、立交桥和密集的高大建筑物的存在导致GPS信号盲区的产生，在传输过程中，因通信或建筑物、树木、桥梁阻隔等原因导致数据缺失，经纬度或速度突变，导致错误数据和数据丢失［11］。为了提高地图匹配的精度，有必要对GPS数据进行预处理，剔除经纬度或速度突变的数据并插值补全缺失的数据［12］。

2.2 候选路段的确定

误差区域是指包含车辆真实位置的区域，确定候选路段之前首先要确定误差区域。圆概率误差（R95＝2DRMS／1.2。其中：2DRMS 为GPS接收机的双倍距离均方根差）是在以GPS接收机天线真实位置为圆心的圆内、偏离圆心概率为95%的二维点位精度分布度量。也即是说，GPS接收机接收到的测量值以95%的概率落在以GPS接收机天线真实位置为圆心、R95为半径的圆内。因此以GPS定位点为圆心，圆概率误差为半径的圆形区域可以确定1个误差圆区域，并从电子地图数据库中提取出与该误差圆相交的路段集L＝｛l1，l2，…，ln｝。考虑路网拓扑关系，从路段集L中取出与上1 个匹配道路有邻接关系的路段作为候选路段。如图2，点O是待匹配的GPS定位点，圆O是误差圆，则与该误差圆相交的路段集为L＝｛1，2，…，7｝，当前时刻车辆行驶在道路1上，则下一时刻车辆只能出现在与道路1相连的道路2，道路3，道路4上，故候选路段为道路2，道路3，道路4。

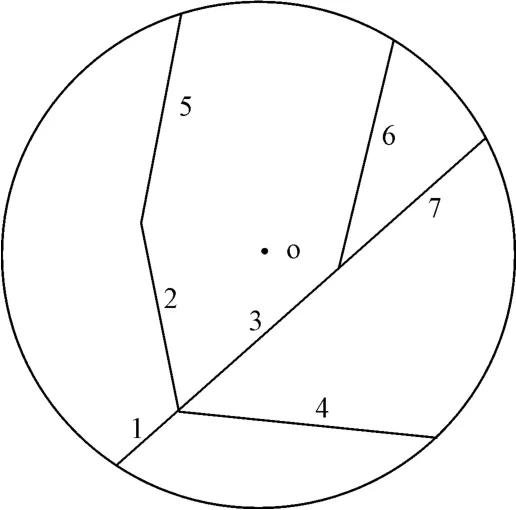
图2 候选路段的选择Fig.2 Choice of the candidate roads

2.3 匹配路段的确定

综合算法采用最小二乘法进行曲线拟合，设观测点的坐标为Pi（xi，yi）（i＝1，2，…，n）。用1个m次多项式y＝a0＋a1x＋…＋amxm来拟合n个观测点数据，使得偏差的平方和最小。偏差的平方和

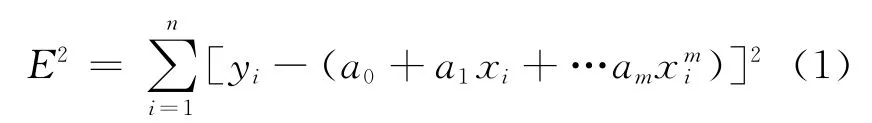
为了求得符合条件的aj（j＝0，1，…，m），对等式右边求aj偏导数，并令这些偏导数等于0。将等式化简并写成矩阵形式，就可以得到下面的矩阵。

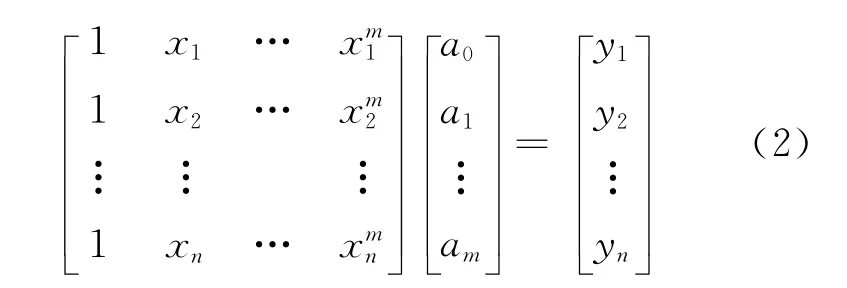
也就是说XA＝Y，那么A＝（XTX）－1XTY，这样就得到了系数矩阵。

电子地图中的路段是用直线段或折线来近似的，由于车辆在道路上行驶的这个前提，在一定的行驶距离内，可以用直线拟合车辆的行驶轨迹。根据道路本身的最短长度，本文选取4个观测点，作1次曲线拟合，即直线拟合。由上述的曲线拟合的原理求得轨迹拟合的直线斜率

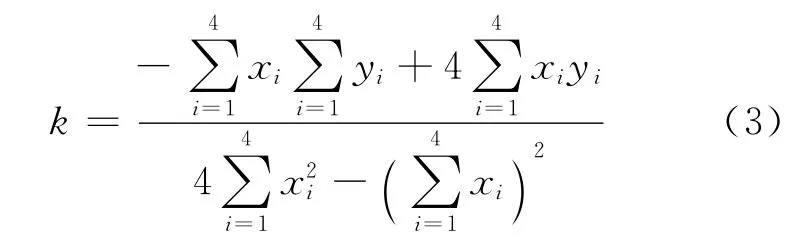
式中：（xi，yi），i＝1，2，3，4为4个GPS定位点的坐标。

k反映了车辆大致行驶方向，在测量误差允许的范围内，认为和轨迹夹角30°以内的路段是可以接受的。从而列出综合算法的评价函数z［13］为

式中：k0为候选路段的斜率；d为测量位置点到候选路段的垂直投影距离；R为误差圆半径，w1，w2为夹角和距离的权值。选取使评价函数最小的候选路段作为匹配路段。由于方向权重高于距离权重，本文取w1＝0.6，w2＝0.4。

2.4 匹配点的确定

选择了匹配路段后，用垂直投影法确定匹配点，而且要保证匹配点在路段内。设定位点为D（x，y），其匹配路段2 端点坐标为S（x1，y1），E（x2，y2），投影点为N（x0，y0），x0，y0根据式（5）得出，d1为投影点N到S的距离，d2为N到E的距离。比较N与S，E的坐标，若N在线段内，N

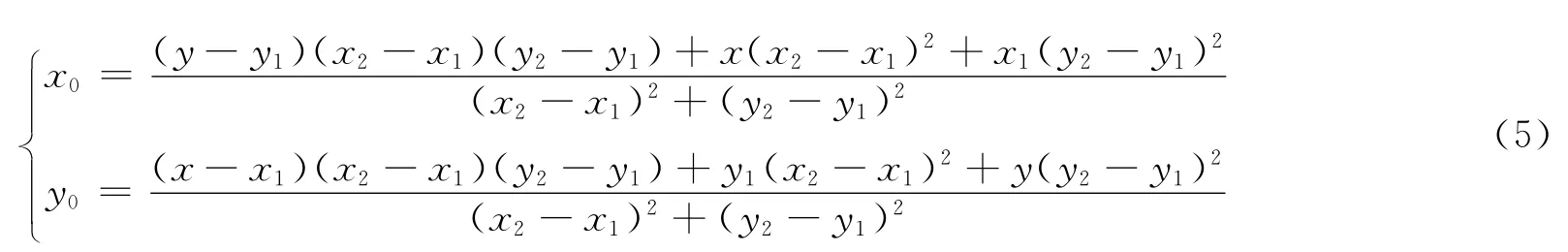
即为匹配点，如图3（a）；若N 不在线段内，且d1＞d2，匹配点为E；否则匹配点为S，见图3（b），（c）。

3 综合算法的实验验证

图4为终端号为22的北京市物流电动出租车的部分行驶轨迹，行驶方向为万红路→酒仙桥东路→酒仙桥北路。由于GPS定位误差的存在，使得部分定位点之间间隔过大且定位点与道路偏离。采用本文提出的综合算法解决这些问题，主要完成3个任务。

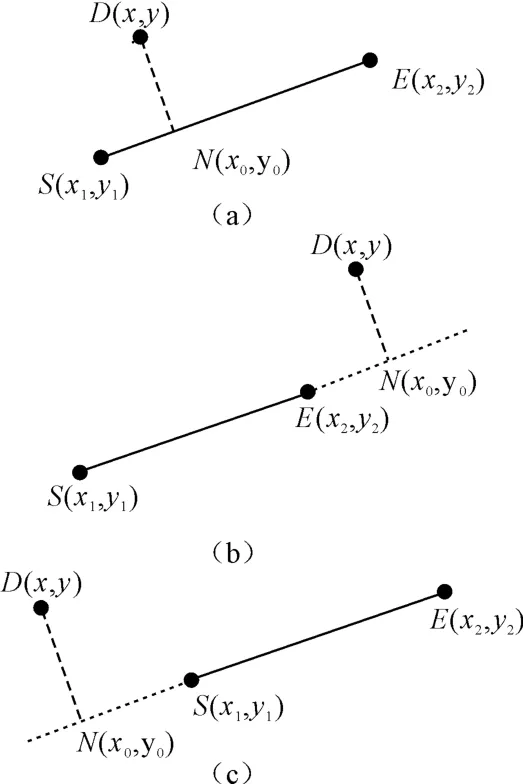
图3 匹配点的确定Fig.3 Confirmation of the matching point

1）预处理GPS 数据，使其符合车辆行驶规律。

2）匹配车辆定位点到正确的路段上。3）确定车辆在路段上的位置。

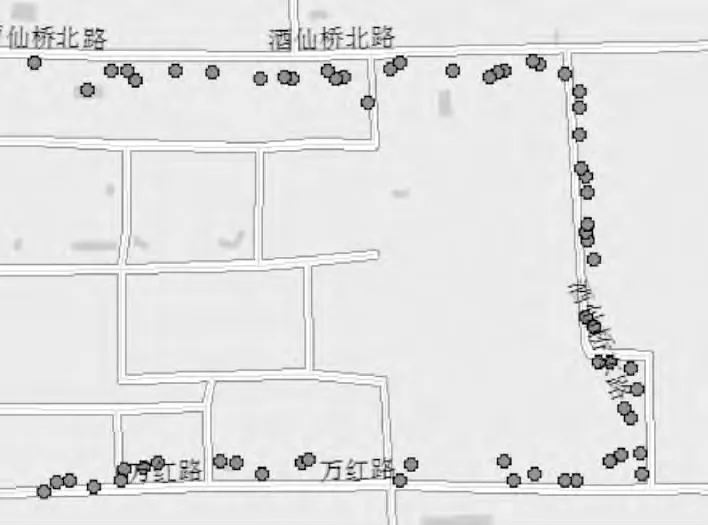
图4 GPS定位点Fig.4 Locating points

GPS接收机每5s接收1次数据，因此以5s为间隔插值补全GPS 数据，由物流电动车内的GPS接收机的双倍距离均方根差得到误差圆半径为66.7 m，然后按综合算法流程进行候选路段、匹配路段和匹配点的确定。图5显示利用本文算法的匹配结果。图6是基于曲线拟合算法得到的匹配结果，由于图中上下2条平行路段距离比较近且部分定位点偏离路段的距离相对较大，所以这2条路段都被包含在误差圆内，基于曲线拟合的地图匹配算法又有其自身的局限性，故出现了图6所示的错误匹配。

将综合算法应用到多个样本进行实验验证，匹配率都在95%以上，单点匹配时间均在5 ms以内。由于综合算法显著地缩小了候选路段的范围，而影响地图匹配算法实时性的主要因素就是候选路段的确定，故其减少了匹配时间。表1所示为综合算法与基于曲线拟合的算法之间匹配率和单点匹配时间的对比。

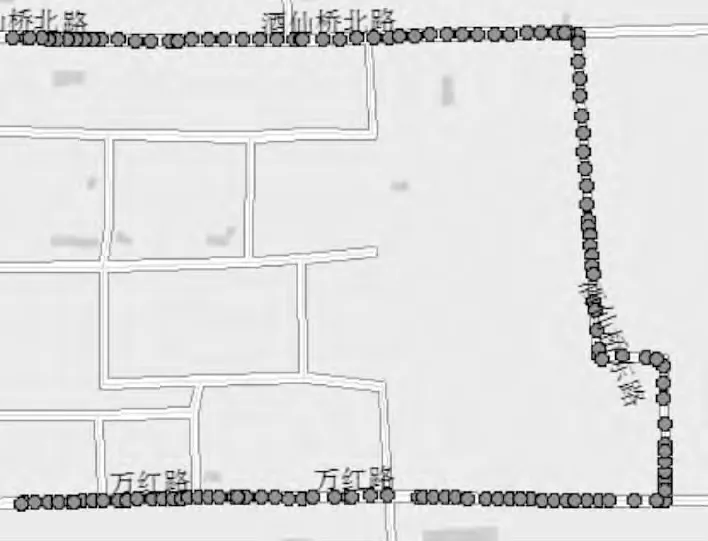
图5 综合算法匹配结果Fig.5 The matching result of comprehensive algorithm

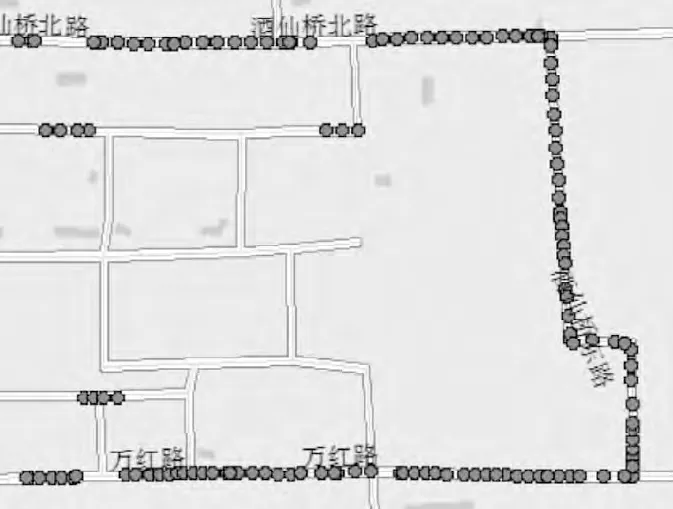
图6 基于曲线拟合算法匹配结果Fig.6 The matching result of curve fitting algorithm

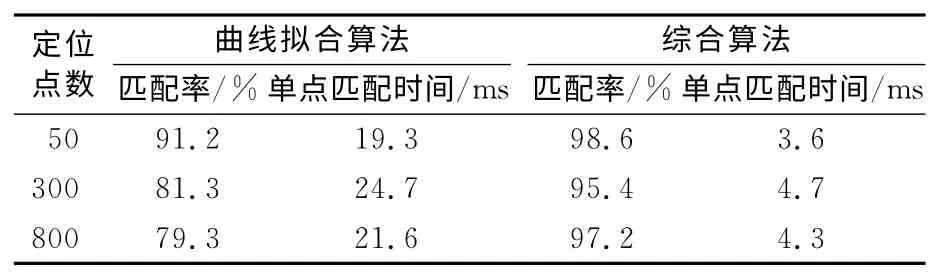
表1 实验结果Tab.1 Experimental results

实验结果表明：本文提出的综合算法能比较精确的把定位点匹配到道路上，能解决基于曲线拟合匹配算法对比较靠近的平行路段进行匹配时容易出错的问题，因此，综合算法能应用到地图匹配的实践中。

4 结束语

笔者提出1种基于曲线拟合和网络拓扑的综合地图匹配算法，详细描述了匹配的4个步骤：数据预处理、候选路段的确定、匹配路段的确定和匹配点的确定。最后将该算法应用到实际的匹配工作中，运行结果表明：该算法精度高、效率好，能解决基于曲线拟合算法在靠近的平行路段匹配率不佳的问题，具有很好的实用价值。

笔者所指的算法没有考虑立交桥区域内的地图匹配，可在此方面做进一步的研究。

［1］White C E，Bernstein D，Komhauser A L.Some map matching algorithms for personal navigation assistants［J］.Transportation Research Part C，2000（8）：91－108.

［2］张 攀，朱敦尧.车载导航地图服务发展探讨［J］.交通信息与安全，2013，31（5）：127－130.Zhang Pan，Zhu Dunyao.Development of car navigation map service［J］.Jounal of Transport Information and safety，2013，31（5）：127－130.（in Chinese）

［3］曾吉全.GPS车辆自导航系统关键技术研究［D］.西安：西安电子科技大学通信工程学院，2004.Zeng Jiquan.The study of key technology of vehicle navigation system［D］.Xi′an：School of Telecommunications Engineering of Xidian University，2004.（in Chinese）

［4］Quddusma，Washingtonyo，Robertbn.Current map－matching algorithms for transport applications：state of the art and future research directions［J］.Transportation Research Part C，2007（15）：312－328.

［5］卢文涛，周银东，梅顺良，等.基于拓扑结构的地图匹配算法研究［J］.测控技术，2010，29（6）：73－76.Lu Wentao，Zhou Yindong，Mei Shunliang，et al.The research of map matching algorithm based on topology structure［J］.Measurement and Control Technology，2010，29（6）：73－76.（in Chinese）

［6］胡 林，谷正气，杨 易.基于权值D－S证据理论的车辆导航地图匹配［J］.中国公路学报，2008，21（2）：116－120.Hu Lin，Gu Zhengqi，Yang Yi.The vehicle navigation system map matching based on D－S theory［J］.China Journal of Highway and Transport，2008，21（2）：116－120.（in Chinese）

［7］苏海滨，王光政，王继东.基于模糊神经网络的地图匹配算法［J］.北京科技大学学报，2012，34（1）：43－47.Su Haibin，Wang Guangzheng，Wang Jidong.The map matching algorithm based on fuzzy nerve network［J］.Journal of Beijing Science and Technology University，2012，34（1）：43－47.（in Chinese）

［8］Velaga Nagendra R，Quddus Mohammed A，Bristow Abigail L.Improving the performance of a topological map－matching algorithm through error detection and correction［J］.Intelligent Transportation System，2012，16（3）：147－158.

［9］钟海丽，童瑞华，李 军.GPS定位与地图匹配方法的研究［J］.小型微型计算机系统，2003，24（1）：109－113.Zhong Haili，Tong Ruihua，Li Jun.The research of GPS localization and map－matching method［J］.Small Microcomputer System，2003，24（1）：109－113.（in Chinese）

［10］Li Liang，Quddus Mohammed，Zhao Lin.High accuracy tightly－coupled integrity monitoring algorithm for map－matching［J］.Transportation Research Part C，2013（36）：13－26.

［11］王志建，王 力，汪 健.基于拓扑判断的海量GPS 数据延时地图匹配算法［J］.西南交通大学学报，2012，47（5）：861－866.Wang Zhijian，Wang Li，Wang Jian.Delay map matching algorithm of mass gps data based on topological judgment［J］.Journal of Southwest Jiantong University，2012，47（5）：861－866.（in Chinese）

［12］张达夫，张昕明.基于时空特性的GPS轨迹数据压缩算法［J］.交通信息与安全，2013，31（3）：6－9.Zhang Dafu，Zhang Xinming.A spatiotemporal compression algorithm for GPS trajectory data［J］.Jounal of Transport Information and Safety，2013，31（3）：6－9.（in Chinese）

［13］周 颖，程荫杭.基于曲线拟合的地图匹配算法［J］.交通运输系统工程与信息，2004，4（2）：68－70.Zhou Ying，Cheng Yinhang.Map－matching algorithm based on curve－fitting model［J］.Journal of Transportation Systems Engineering and Information Technology，2004，4（2）：68－70.（in Chinese）