桥墩遭受船舶撞击的数值模拟法及其动态响应的研究＊

田 力 邱志雄

（1.天津大学建筑工程学院 天津 300072；2.天津大学土木工程结构与安全教育部重点实验室 天津 300072；3.曼彻斯特大学机械航天与土木工程学院 英国 曼彻斯特M13 9PL）

在运输繁忙的内河与沿海航道上，船舶碰撞桥梁的事故时常发生，造成桥梁和船舶的损伤。特别是近几十年来，我国经济迅猛发展，在城市化进程加速过程中，跨江、跨海大桥的大量兴建，以及水运需求量的不断增长使得各运输水域的船舶通航量大幅度增加。这一系列的变化极大地方便了人们的生活，促进了社会的发展，但同时也使得船舶撞击桥梁的事件发生的更加频繁。

在研究船－桥碰撞问题时，获得准确的碰撞力、变形等响应是研究的主要目的。由于桥梁配筋的复杂性，已有的数值模拟研究中的桥梁下部结构多采用整体式模型，通过提高混凝土的强度来考虑钢筋的影响。为了更好的模拟船－桥碰撞的真实情况，笔者建立了分离式的桥梁下部结构模型，来分析不考虑流体影响、附加质量和流构耦合3种模型下桥墩在遭受船舶撞击时的动态响应。

1 计算模型和材料

1.1 船舶模型

笔者参考了某内河航道3 000t散货船的线型数据和结构形式建立了船舶的计算模型。建模时对船首部分进行了精细化建模，船身则近似按刚体处理，船首结构见图1。计算中，取船舶的航速为4.5m／s。

图1 船首有限元网格划分与船首内部结构Fig.1 Finite element mesh of ship bow and its internal structrue

1.2 桥墩模型

参考了某铁路桥梁建立了桥墩计算模型，其尺寸见表1，示意图见图2。在建立桥墩分离式模型时，对钢筋进行了一定的简化，只考虑了起主要受力作用的钢筋。桥墩钢筋配筋见图3。为简化起见，桥墩、承台和桩的混凝土强度都取C40，钢筋均取HRB400。钢筋和混凝土之间通过共节点的方法来模拟钢筋、混凝土的共同作用。

用粘弹性人工边界来模拟土体四周边界条件。通过在土体边界处延伸一定厚度的实体单元，将该层单元最外层固定，依据文献［1］的方法计算边界单元的等效剪切模量和弹性模量。由于桥梁桩基周围为较硬的粘性土层，下部为基岩，因此桩基按嵌岩桩处理，通过定义自动面面接触，考虑桩土间的相互作用，取桩土间的摩擦系数为0.312［2］。

表1 被撞桥墩主要尺寸Tab.1 Main size of the impacted pier

图2 桥墩计算模型Fig.2 Calculation model of the impacted pier

图3 桥墩配筋示意图Fig.3 Calculation model of steel bar

1.3 附加质量模型

对于船－船碰撞问题，附加质量法被普遍用来近似考虑流体对碰撞的影响。经典的做法是假定碰撞船舶在流体中运动时，附带周围流体的质量为船舶总质量的0.02～0.07倍［3］，然后通过增加船体远离碰撞区域的的材料密度来达到附加质量的目的。但在船－桥碰撞问题中，如果只考虑流体对船舶的影响，则忽略了流体对结构的影响。除考虑船体附加质量的外，也以附加质量的形式来考虑流体对桥梁下部结构的作用。

工程界主要基于Morison方程［4］来求解细长柱体在流体中所受的动水压力，但要求与波长与柱体截面尺寸的比值应足够小（以圆形为例，D／L＜0.2）。在船桥碰撞问题中，考虑到船－桥碰撞的瞬态性，波浪运动速度与结构响应速度相比很小，因此，可不考虑波浪的运动，假定水静止。此时流水对桥梁下部结构的动水压力的表达式为

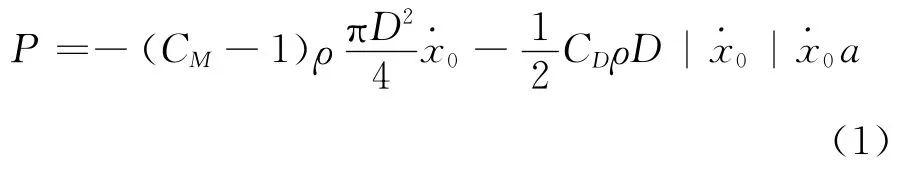
式中：第1项为惯性力项（由附加质量引起）；第2项为阻 尼力项；ρ为水体密度和为结构绝对速度和绝对加速度；D为柱体直径；CD为粘性摩阻力系数；CM为质量系数。研究表明，忽略阻尼力项对桥梁结构动力响应的影响不超过1.5%［5］，故结构所受动水压力由附加质量：

来反映。因此，针对文中船－桥碰撞计算模型，首先分别计算桥梁下部入水构件（圆端形墩柱、矩形承台和群桩）的附加质量，然后在建立有限元模型时，采用LS－DYNA 中质量单元来计及构件相应部位的动水压力作用。在推导附加质量计算式（2）时，假定水是静止的，即其波长L足够大，满足用Morison方程计算桥梁下部结构入水构件的附加质量最小尺度的要求。

1）圆端形墩柱附加质量计算。式（2）能够计算圆形、矩形墩柱的附加质量，对于圆端形截面墩柱（见图4），可将其等效为1个圆形和1个矩形截面分别计算，然后将矩形墩柱计算的附加质量乘以矩形截面参与系数后再与圆形截面计算附加质量组合［6］。

取质量系数CM＝2.0；对矩形截面墩柱，取质量系数CM＝1.51（D／L）－0.17＋1。水的密度ρ为1 000kg／m3，由式（3）和（4）计算可得圆端形墩柱单位高度附加水质量。

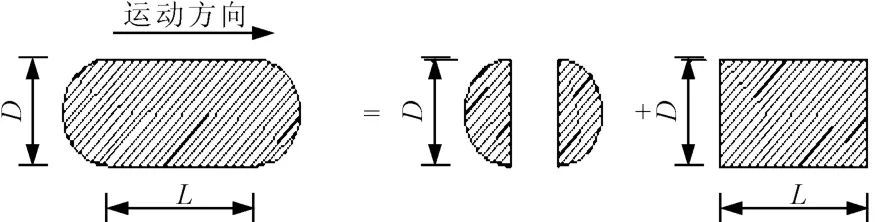
图4 圆端形桥墩截面等效形式Fig.4 Equivalent form of the round－ended section of the pier

2）矩形承台附加质量计算。矩形承台单位高度附加质量的计算方法与上文圆端形墩柱中矩形截面的计算方法相同，此处不再赘述。

3）群桩附加质量计算。单根桩体单位高度附加质量的计算方法与圆端形墩柱中圆形截面的计算方法相同，但对于群桩体，还需考虑柱体之间的相互遮蔽及干扰效应，而这种效应的强弱程度主要依赖于桩体间距L与桩径D的比值［4］。当L／D＞4时，柱体间的这种相互遮蔽和干扰则可忽略不计；当L／D≤4时，则需要考虑，即将单桩所受的动水压力乘以相应的群桩系数K［7］。我国《海港水文规范》（JTJ 213—98）中建议的群桩系数，见表2。对于文中桩基排列情况（见图5），群桩系数取K＝1.187 5，群桩单位高度附加质量计算结果见表3。

图5 群桩平面布置Fig.5 Layout of the pile group

表2 群桩系数KTab.2 Effect coefficient Kof the pile group

笔者所建立的船－桥附加质量计算模型见图6，流体对船舶的影响仍沿用文献［4］的做法，即船体附加质量取0.04倍船舶总质量，该部分附加质量通过增大船体中后部分刚体单元的密度来实现。在船体与承台、船体与桥墩之间定义了自动面面接触算法［7］，用来模拟船体对桥墩的撞击作用。船艏自身通过定义自动单面接触来模拟碰撞引起的塑性变形、褶皱及崩溃的过程。其中，参考文献［8］，钢材与混凝土之间的摩擦系数取0.3，混凝土与混凝土之间的摩擦系数取0.6。

1.4 流构耦合计算模型

为了在不花费过多计算资源的前提下，得到最接近真实碰撞的计算结果，仅考虑碰撞区域周围的局部流场影响。流体范围为以桥墩轴线为中点，分别取2倍船宽、1.5倍船宽作为流场区域的长和宽，流场深度取9m，流体边界定义为无反射边界，计算模型见图7。耦合面包含了船艏外板以及被流场覆盖的墩柱、承台、桩体和土体的外表面，流构耦合时船艏对结构的撞击作用、桩土动力相互作用、结构的变形、舷外流场的改变及其动力作用将同步计算，与不考虑流场影响的情况相比，流构耦合模型是与真实碰撞最好的物理近似。

表3 桥梁下部结构单位高度附加水质量Tab.3 Additional water mass on unit height of the substructures of pier

图6 船－桥碰撞的附加质量计算模型Fig.6 Calculation model of the ship－bridge collision with the additional mass

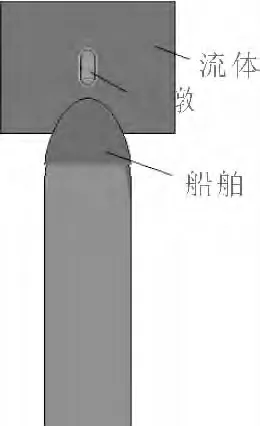
图7 流构耦合计算模型Fig.7 Calculation model of the ship－bridge collision considering the fluid－solid coupling effect

1.5 材料模型

1）混凝土材料模型。混凝土采用LS－DYNA中的HJC模型。该模型是 T.J.Holmquist，G.R.Johnson和W.H.Cook针对混凝土在大应变，高应变率和高压强的环境下提出来的一种计算本构模型。HJC 模型考虑了混凝土的损伤累积及应变率效应，数值计算结果能和实验数据较好的稳合，因此，被广泛的的应用于在爆炸和冲击等动力学问题。

笔者参考G.R.Johnson等提出的静态抗压强度为48 MPa、拉伸强度为4 MPa 及密度为2 440kg／m3的混凝土计算参数和文献［9－11］的计算方法确定文中使用的混凝土材料参数，其主要计算参数见表4。

表4 混凝土HJC模型材料参数Tab.4 Material parameters of HJC model

2）钢筋和船艏材料模型。桥梁下部结构的钢筋以及船体所用的壳体材料均采用LS－DYNA 中的随动强化双线性模型（＊MAT－PLASTIC－KINEMATIC）［12］。材料参数分别见表5、表6。

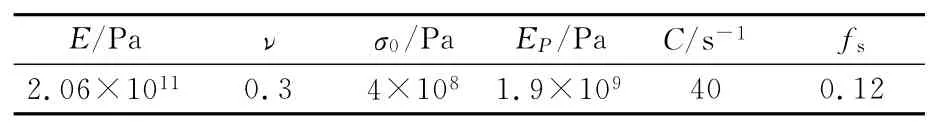
表5 钢筋材料参数Tab.5 Material parameters of steel bar

3）土体材料模型。土体材料模型采用的是LS－DYNA 中的DruckerPrager［13］模型在LSDYNA 程序中，Drucker－Prager模型的数据需要输入6个值：密度、泊松比、剪切模量、粘聚力、内摩擦角、膨胀角。其中膨胀角是用来控制体积膨胀的大小，对压实的颗粒状材料，当材料受剪时，颗粒将会膨胀，如果膨胀角等于0，就不会发生体积膨胀。默认情况下膨胀角设为0。文中的土体材料参数见表7［14］。

表7 土体材料参数Tab.7 Material parameters of soil

2 船撞桥墩数值仿真分析

2.1 碰撞前的初始状态

模拟过程的计算时间为3s，分为2个阶段：加载阶段和碰撞阶段。加载阶段的计算时间为1s，在模拟撞击过程之前，先通过对桥墩施加重力和上部荷载使其处于静力平衡状态。在施加重力和上部荷载时，分2步加载：荷载首先由零开始逐渐增加至加载值，然后保持荷载不变，直到碰撞结束。

2.2 不同计算模型的能量转化

检查系统总能量是否合理、各能量转化关系是否正确、沙漏能是否得到了有效控制是显示动力分析中判别计算结果合理性的1种重要方法。图8～图10 给出了3 种计算模型的总能量、内能、动能和沙漏能的变化规律。由图可见，3种计算模型在碰撞过程中，系统的总能量基本守恒，沙漏能维持在较低的水平，低于总能量、内能的10%以下，90%以上的动能转化为内能，说明计算结果合理可靠［11］。不同的计算模型在碰撞过程中的能量变化规律基本相同，能量曲线具有基本相同的变化趋势。流构耦合模型的内能和总能量较其他两种模型大，该部分能量主要来自流体的初始内能。由于在碰撞中，船首与承台之间存在相互滑动，因此船舶和承台接触界面滑移能不为零，其大小与碰撞力和船首与承台的摩擦系数有关。

图8 不考虑流体模型能量变化Fig.8 Energy change of no－water model

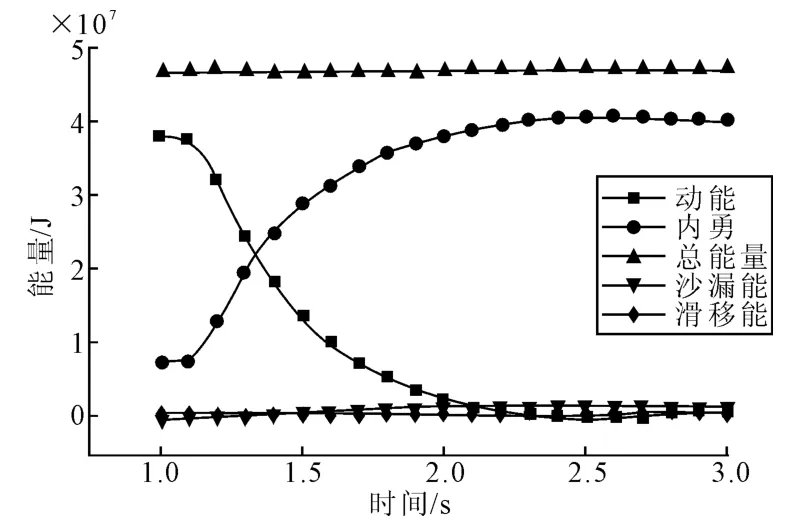
图9 附加质量模型能量变化Fig.9 Energy change of the additional mass model

图11中，碰撞力为0说明船首与承台已经分离。在大约2.6s时，不考虑流体影响计算模型和附加质量计算模型的碰撞力都减小为0，而流固耦合模型的碰撞力减小为0的时间要晚0.2s左右，这是由于流体的阻力使得船舶背离桥墩的速度增加缓慢，因此船舶与承台接触的时间更长。从船速变化曲线图12也可以看到流构耦合计算模型的船速出现负值和达到稳定的时间都比其余2种计算模型要晚，对应了碰撞力时程曲线中的规律。

图10 流构耦合模型能量变化Fig.10 Energy change of the fluid－solid coupling model

图11 不同模型碰撞力时程曲线Fig.11 Collision force－time curves of different models

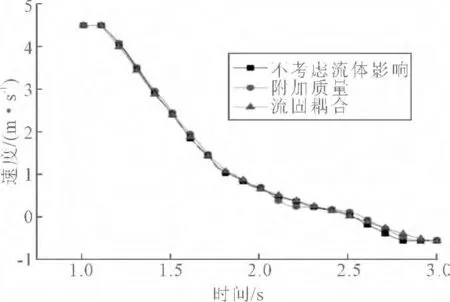
图12 不同计算模型船速变化时程曲线Fig.12 Velocity－time curves of ships of different models

2.3 桥墩位移响应

2.3.1 桥墩位移响应

图13和图14给出了船舶撞击下桥墩顶面和承台顶面的水平位移时间历程。对比图中的曲线可知，3种计算模型的位移响应在碰撞前期基本是一致的，碰撞中后期，文所采用的附加质量模型的墩顶和承台顶面位移要稍大于其余2种模型，这表明在船桥碰撞问题中以附加质量的形式来考虑流体的影响时，会稍微夸大碰撞中桥墩的位移响应，但差别并不大，对于桥墩的防撞设计是偏于安全的。

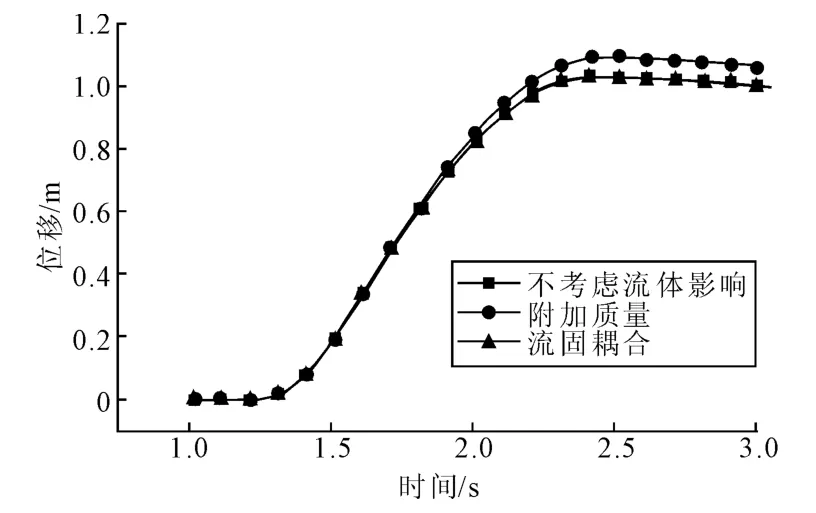
图13 不同计算模型墩顶水平位移时程曲线Fig.13 Horizontal displacement－time curves of pier top of different models

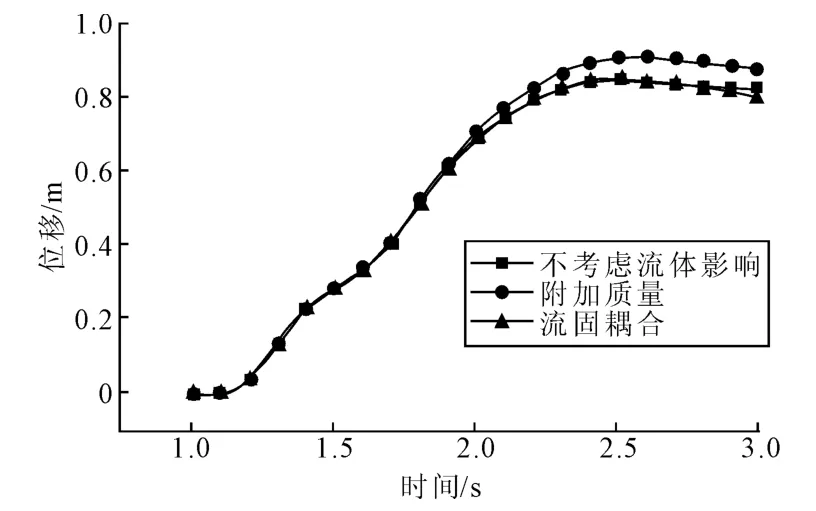
图14 不同计算模型承台顶面水平位移时程曲线Fig.14 Horizontal displacement－time curves of pile caps of different models

2.5 桥墩应力分析

表8为不同计算时刻3种模型的最大有效应力比较。由表3可见，不同模型的桥墩最大有效应力的发展规律基本一致，在3s时桥墩的最大有效应力有所减少是因为桥墩的变形在3s时有所恢复。对比3种模型在各时刻有效应力可以发现，在数值上3种计算结果都很接近，说明流体对于结构有效应力的影响比较小。

在计算过程中，桥墩会出现2个高应力区：桩与土体表面接触区域和桩与承台连接区域。桩基与土体表面接触区域出现高应力是因为桥墩在遭受撞击时，发生了较大的侧向变形，而土体的存在限制了土体以下部分桩身的变形，而土体以上部分的桩基由于没有约束，能发生较大的侧向位移，因此桩基会在土体表面处发生较大的弯曲变形。桩基与承台连接处出现高应力是因为承台平面内的刚度要大于8根桩平面内刚度的总和，所以在遭受船舶撞击时承台多发生平移和旋转，进而导致连接处的桩基发生较大的变形。

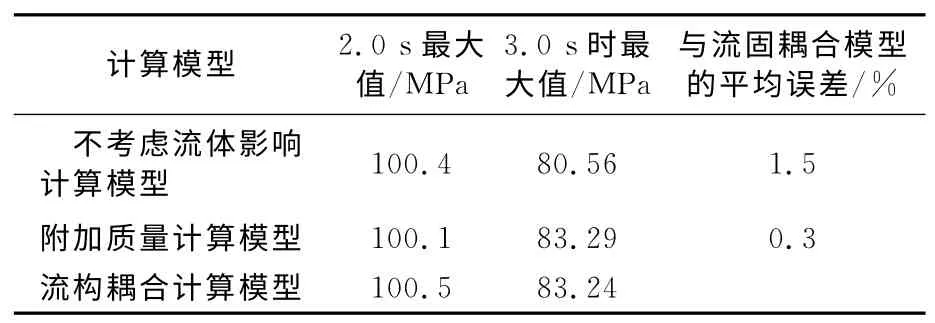
表8 不同计算模型桥墩最大有效应力比较Tab.8 Comparison of the maximum effective stresses of the different calculation models

3 计算效率对比

对于本文中所有计算模型均在HPZ800工作站进行求解。不同计算模型在计算时间及计算机软硬件同等条件下，所消耗的CPU 时间相差较大。其中，不考虑流体影响的计算模型和附加质量计算模型所用CPU 时间基本相同；与其他计算模型相比，流构耦合计算模型所用CPU 总时间明显偏大，为其他计算模型的2.5倍左右。而在流固耦合模型中，耦合计算及大量单元的处理分别占CPU 总时间的10%和88%左右。这表明，本文所提出的基于附加质量的船－桥碰撞模型，具有较高的计算效率。

4 结束语

通过3种船舶撞击桥墩模型的模拟与分析可以得到以下结论。

1）3种计算模型的能量变化具有相同的规律。其中流固耦合模型的系统总能量和内能略大于其余2种计算模型。

2）3种计算模型的船舶碰撞力基本一致，流体的存在对于碰撞力的影响要小。

3）桥墩的位移要滞后于承台的位移。附加质量模型的桥墩和承台的位移要稍大于其余2种计算模型。

4）3种计算模型的桥墩在不同计算时刻有效应力的最大值相差不大。桩基与土体顶面交界处和桩基与承台连接处计算中出现高应力区。

5）附加质量计算模型在保证计算精度的同时，具有比流构耦合模型更高的计算效率。

［1］谷 音，刘晶波，杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元［J］.工程力学，2007（12）：31－37.Gu Yin，Liu Jingbo，Du Yixin.3D Consistent viscous－spring artificial boundary and viscous－spring boundary element［J］.Engineering Mechanics，2007（12）：31－37.（in Chinese）.

［2］许宏发，吴华杰，郭少平，等.桩土接触面单元参数分析［J］.探矿工程，20025）：10－12.Xu Hongfa，Wu Huajie，Guo Shaoping，et al.Parameter analysis of pile soil contact element［J］.Prospecting Engineering，2002（5）：10－12.（in Chinese）.

［3］王自力，蒋志勇，顾永宁.船舶碰撞数值仿真的附加质量模型［J］.爆炸与冲击，2002，22（4）：321－325.Wang Zili，Jiang Zhiyong，Gu Yongning.The add mass numerical simulation model of ship collision［J］.Explosion and Impact，2002，22（4）：321－325.（in Chinese）.

［4］竺艳蓉.海洋工程波浪力学［M］.天津：天津大学出版社，1991.Lan Yanrong，Wave mechanics for ocean engineering［M］.Tianjin：Tianjin University Press，1991.（in Chinese）.

［5］赖 伟，王君杰，胡世德.地震下桥墩动水压力分析［J］.同济大学学报：自然科学版，2004（1）：1－5.Lai Wei.Wang Junjie，Hu Shide.Earthquake induced hydrodynamic pressure on bridge pier［J］，Journal of Tongji University：Natural Science Edition，2004（1）：1－5.（in Chinese）.

［6］杨万理.深水桥梁动水压力分析方法研究［D］.成都：西南交通大学，2012.Yang Wanli.Deep water bridge dynamic water pressure analysis method study［D］.Chengdu：Southwest Jiaotong University，2012.（in Chinese）.

［7］阙水杰，张 南，樊文才.桥墩遭受船舶撞击的有限元仿真分析［J］.交通信息与安全，2010，28（1）：130－134.Que Shuijie，Zhang Nan，Fan Wencai.Finite element simulation analysis of a pier under ship collision［J］.Journal of Transprot Information and Safe－ty，2010，28（1）：130－134.（in Chinese）.

［8］律文田.静动荷载作用下铁路桥梁桩基的动力特性研究［D］.长沙：中南大学，2005.Lv Wentian.Under static and dynamic load characteristics of railway bridge pile foundation research［D］，Changsha：Central South University，2005.（in Chinese）.

［9］刘建成，顾永宁.基于整船整桥模型的船桥碰撞数值仿真［J］.工程力学，2003（5）：155－162.Liu Jiancheng，Gu Yongning.Simulation of ship bridge head－on collision based on finite element model of whole［J］.Engineering Mechanics，2003（5）：155－162.（in Chinese）.

［10］张凤国，李恩征.混凝土撞击损伤模型参数的确定方法［J］.弹道学报，2001（4）：12－16.Zhang Fengguo，Li Enzheng.The methods for determining the parameters of concrete impact damage model［J］.Journal of Ballistics，2001（4）：12－16.（in Chinese）.

［11］黄 飞.船舶撞击下连续梁桥的桥墩动力响应及整桥局部倒塌研究［D］.天津：天津大学，2014.Huang Fei.The dynamic response and partial collapse study of continuous girder bridge pier and under ship collision［D］.Tianjin：Tianjin University，2014.（in Chinese）.

［12］Hallquist J O.LS－DYNA keyword user’s manual［M］.California：Livermore Software Technology Corporation，2007.

［13］白金泽.LS－DYNA3D理论基础与实例分析［M］.北京：科学出版社，2005.Bai Jinze.LS－DYNA3Dtheoretical basis and case analysis［M］.Beijing：Science Press，2005.（in Chinese）.

［14］Liu Jiancheng，Gu Yongning.Simulation of shipbridge head－on collision based on finite element modle of whole ship－bridge［J］.Engineering Mechanics，2003（5）：155－162.