基于时间序列相似性搜索的交通流短时预测方法＊

杨兆升 邴其春 周熙阳 马明辉 李晓文

（1.吉林大学交通学院 长春 130025；2.吉林大学汽车仿真与控制国家重点实验室 长春 130025；3.吉林大学吉林省道路交通重点实验室 长春 130025）

0 引言

准确、可靠的交通流短时预测信息是交通控制和交通诱导等多项ITS核心功能的基础和关键，对于缓解交通拥堵问题具有重要意义。然而，由于检测器获取的交通流数据具有较强的时间滞后性，不能准确代表实时交通状态，要想掌握实时动态交通流运行状态就必须进行短时交通流预测。迄今为止，各国交通工程研究者已经开发了多种预测模型和方法。较早期的预测方法主要有自回归模型（AR）、移动平均模型（MA）、自回归移动平均模型（ARMA）、历史平均模型（HA），等等，其预测结果主要服务于自适应交通控制系统。随着对交通流特性的深入研究以及人工智能技术的发展，一批高精度、高可靠度的预测方法被相继提出，主要包括时间序列模型［1］、非参数回归模型［2］、卡尔曼滤波模型［3］、小波理论模型［4］、支持向量机模型［5］、神经网络模型［6－8］等。然而，现有的交通流短时预测方法普遍存在两方面问题，一方面已有的研究成果主要集中于预测模型的整合优化，忽视了对交通流数据自身特性的有效利用。具体来说，目前大多数预测模型以相邻N个时间间隔交通流数据作为模型输入值，从而导致预测误差较大。另一方面，绝大多数交通流预测仅进行一步预测，无法充分描述交通状态的未来发展趋势。针对目前交通流预测中存在的问题，为了进一步提高交通流预测信息的准确性和可靠性，笔者提出1种基于时间序列相似性搜索的交通流短时多步预测方法。

1 模型基本原理

1.1 交通流时间序列相似性搜索

交通流时间序列相似性搜索的目的是为了在海量的交通流数据中寻找与预测时刻最相关的历史数据作为预测模型的输入数据。由于原始交通流数据存在较大的随机波动，直接采用原始交通流时间序列数据进行相似性搜索不仅效率低下，甚至会影响时间序列搜索的准确性和可靠性。为提高搜索的效率和准确性，众多时间序列模式表示方法相继提出，主要包括离散傅里叶变换法［9］、离散小波变换方法［10］、奇异值表示法［11］、符号表示法［12］、分段线性表示法［13］，以及界标模型［14］等。其中，界标模型不仅能够保留原始交通流数据的局部特征，而且形象、直观，具有明显的高效性。因此，笔者选用界标模型作为交通流时间序列数据的模式表示方法。

界标模型由Perng等人最先提出，是1种集相似性模型和数据模型为一体的方法。如果将曲线n阶导数为0的点称为曲线的n阶界标，则局部极大、极小值点就是曲线的一阶界标，拐点则为二阶界标。交通流时间序列往往含有随机噪声，界标模型提出了最小距离／百分比规则作为平滑方法来消除噪声干扰，如图1所示。具体定义如下。

假定1个界标序列为｛（x1，y1），…，（xi，yi），…，（xm，ym）｝。其中：xi为第i个界标在原始时间序列数据中的位置；yi为其对应的时间序列值。给定最小距离D和最小百分比P，如果（xi，yi）和（xi＋1，yi＋1）满足下述条件时，则可以将它们从界标序列上删除。

这个条件用MDPP（D，P）表示。其中：D为最小距离，表示2个界标之间的最小时间间隔；P为最小百分比，表示相邻2个界标之前幅值变化的最小程度，见图1。

图1 最小距离／最小百分比示意图Fig.1 Minimal distance／percentage principle

界标序列是由数据对来表示的，需用界标距离进行相似性度量。下面给出界标距离相似性度量的定义。

已知2个界标序列L＝｛L1，L2，…，Ln｝和L′＝｛L′1，L′2，…，L′n｝，其中，Li＝（xi，yi），L′i＝（x′i，y′i），则2个序列第k个界标之间的距离为

Δk（L，L′）＝（L，L′（L，L′））（2）

2个序列的距离为

式中：‖·‖为矢量范数，如果δtime≤δ′time，δamp≤δ′amp，则（δtime，δamp）≤（δ′time，δ′amp）。

1.2 回声状态网络的数学模型

神经网络模型在交通流预测中被广泛应用，然而由于传统神经网络模型收敛过慢，容易陷入局部最优的缺点，使得神经网络模型在实际应用中受到一定的束缚。针对传统神经网络的缺陷，Jaeger［15］于2001年提出1种新型递归神经网络——回声状态网络（echo state networks，ESN）。

如图2所示，回声状态网络模型由输入层、隐层和输出层构成。u（n）为含有K个输入神经元的输入层激活向量；x（n）为含有N个隐层神经元的隐层激活向量；y（n）为含有L个输出神经元的输出层激活向量。输入单元、隐层单元以及输出单元在n时刻的值分别为

图2 回声网络模型结构图Fig.2 The structure of echo state network model

从结构上讲，ESN 是1种特殊类型的神经网络模型，其基本思想是使用大规模随机连接的递归网络，取代经典神经网络中的中间层，从而简化网络的训练过程［16］。回声状态网络的状态方程为

式中：W，Win，Wback分别为隐层－隐层、输入层－隐层，以及输出层－隐层的连接权矩阵；Wout为输出的权重矩阵。f＝［f1，f2，…，fN］为内部神经元激活函数，fi（i＝1，2，…，N）通常取双曲正切函数，为输出函数，＝1，2，…，L）一般取恒等函数。在网络训练过程中，连接到储备池的权重矩阵W，Win，Wback是随机产生的，在训练过程中固定不变，只有输出的权重矩阵Wout需要通过训练得到。

2 实例验证

2.1 数据来源与描述

实验数据来源于国内某特大城市长约10km快速路上感应线圈检测器采集到的地点交通流数据。该路段设置24个主线检测截面和30个匝道检测截面，安装有88个主线检测器和60个匝道检测器。实验数据的采集时间为2008年9月到10月间连续5个周一，采样间隔为20s。由于20 s交通流数据具有较大的波动性，本文将20s交通流数据合成为5min数据，另外，在交通拥挤判别、交通诱导等实际应用中需要掌握实时和1h内的动态交通信息，因此，本文对5min交通流数据进行12步预测。

图3（a）为同一检测器不同日期采集的交通流数据表现出的相似性，图3（b）为同一车道不同检测截面采集的交通流数据表现出的相似性，图3（c）为同一检测断面不同车道采集的交通流数据表现出的相似性。由图3可见，交通流时间序列数据具有较强的相似性，为本文方法的提出提供了充足的数据支撑。

2.2 参数设置

为验证时间序列数据模式表示的效果，以东侧主线NBDX08（1）固定检测器2008年9月1日07：00～19：00时的交通流数据为例，利用界标模型对交通流时间序列数据进行模式表示，通过对交通流时间序列数据特性的深入研究，采用一阶界标对原始数据进行表示，最小距离D取2，最小百分比P取15%，结果见图4。

由图4可见，通过界标模型的模式表示，原始时间序列中的145个数据压缩为29个界标点，且能够保留原始数据所有的局部特征，由此说明界标模型能够有效的降低原始数据的维数，进而提高相似性搜索的效率。

对时间序列数据进行模式表示之后，就可以根据界标距离对时间序列进行相似性搜索。然而，在相似性搜索的过程中需要确定两个参数，1个是界标序列的长度l，另1个是相似时间序列的个数k，本文以回声状态网络模型多步预测的平均相对误差最小为指标确定两个参数的取值。其中，根据回声状态网络模型关键参数的设定原则，确定储备池参数的具体取值为：储备池内部连接权矩阵的谱半径SR＝0.75，储备池规模N＝50，输入比例因子IS＝0.2，储备池的稀疏程度SD＝0.1。以2008年9月1日、9月8日、9月15日、9月22日4个周一的交通流数据为基础建立历史数据库，采用回声状态网络模型对9月29日的交通流数据进行多步预测。不同参数取值所对应的平均相对误差见表1。

图3 感应线圈交通流数据Fig.3 Traffic flow data from loop detectors

图4 时间序列模式表示效果Fig.4 The effectiveness of pattern representation

表1 对应不同参数的MAPETab.1 The MAPEcorresponding to different parameter values %

由表1可见，当k＝5，l＝4时，多步预测的效果最好，平均相对误差仅为15.5%，因此，相似时间序列的个数k取5，界标序列长度l取4。

2.3 实验结果与分析

为直观展现本文方法的预测效果，图5和图6分别为NBDX08（2）和NBDX16（2）2个固定检测器数据一步预测的结果，从图中可见，通过本文方法的预测值与实际值之间拟合较好，预测误差较小，具有很好的预测效果。

图5 NBDX08（2）检测器数据一步预测效果图Fig.5 The one－step prediction results of NBDX08（2）

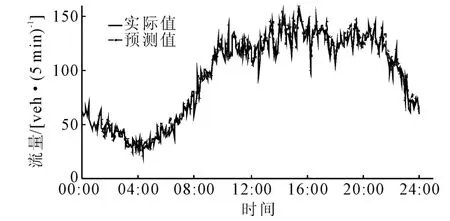
图6 NBDX16（2）检测器数据一步预测效果图Fig.6 The one－step prediction results of NBDX16（2）

为对比分析回声状态网络模型预测的有效性，本文采用自回归移动平均（ARIMA）模型和BP神经网络模型作为对比方法。另外，为验证通过时间序列相似性搜索确定预测模型输入数据的优越性，同时采用以相邻数据为输入数据的回声状态网络模型作为对比方法。其中BP神经网络模型参数选取如下：选取输入单元个数为5，输出单元个数为1，隐层神经元个数为8，其隐层神经元的激活函数为Sigmoid函数，输出层神经元的激活函数为线性函数。自回归移动平均模型的阶数根据AIC准则确定。4种方法的具体预测误差如图7所示。

实验结果表明，短时交通流预测结果的MAPE随着预测步数的增加而增大，两者存在一定的正相关关系。以相邻数据为预测模型输入数据的回声状态网络模型预测精度分别比ARIMA方法和BP神经网络方法提高6.25%和3.85%，说明回声状态网络模型的预测效果优于ARIMA模型和BP 模型。另外，通过比较本文方法和以相邻数据为模型输入数据的回声状态网络模型的预测结果可见，本文方法的MAPE为15.5%，而以相邻数据为模型输入数据的回声状态网络模型的MAPE为17%，说明本文方法能够进一步提高交通流短时预测的精度。

图7 不同方法交通流多步预测效果对比图Fig.7 The MAPE of different methods from one－step to twelve－step prediction

3 结束语

针对交通流数据的相似性特性，在分析现有交通流预测模型存在缺点的基础上，笔者提出了1种基于时间序列相似性搜索的交通流短时多步预测方法，并以我国某特大城市快速路的实测数据进行了实验验证和对比分析。结果表明，本文方法的多步预测效果明显优于对比方法，进一步降低了交通流短时多步预测的误差。

［1］Min W，Wynter L.Real－time road traffic prediction with spatio－temporal correlation［J］.Transportation Research Part C：Emerging Technologies.2011，19（4）：606－616.

［2］Clark S.Traffic prediction using multivariate nonparametric regression［J］.Journal of Transportation Engineering.2003，129（2）：161－168.

［3］杨兆升，朱 中.基于卡尔曼滤波理论的交通流量实时预测模型［J］.中国公路学报，1999，12（3）：63－67.Yang Zhaosheng，Zhu Zhong.A real－time traffic volume prediction model based on the kalman filtering theory［J］.China Journal of Highway and Transport，1999，12（3）：63－67.（in Chinese）.

［4］贺国光，马寿峰，李 宇.基于小波分解与重构的交通流短时预测方法［J］.系统工程理论与实践，2009，9：101－107.He Guoguang，Ma Shoufeng，Li Yu.Study on the short－term forecasting for traffic flow based on wavelet analysis［J］.System Engineering－Theory＆Practice，2009，32（9）：101－107.（in Chinese）.

［5］傅 贵，韩国强，逯 峰，等.基于支持向量机回归的短时交通流预测模型［J］.华南理工大学学报：自然科学版，2013，41（9）：71－76.Fu Gui，Han Guoqiang，Lu Feng，et al.Shortterm traffic flow forecasting model based on support vector machine regression［J］.Journal of South China University of Technology：Natural Science Edition，2013，41（9）：71－76.（in Chinese）.

［6］高 为，陆百川.基于时空特性和RBF 神经网络的短时交通流预测［J］.交通信息与安全，2011，29（1）：16－20.Gao Wei，Lu Baichuan.Short－term traffic flow forecasting based on spatiotemporal characteristics of traffic flow and RBF neural network［J］.Journal of Transport Information and Safety，2011，29（1）：16－20.（in Chinese）.

［7］龚勃文，林赐云，等.基于核自组织映射－前馈神经网络的交通流短时预测［J］.吉林大学学报：工学版，2011，41（4）：939－943.Gong Bowen，Lin Ciyun，et al.Short－term traffic flow prediction based on KSOM－BP neural network［J］.Journal of Jilin University：Engineering and Technology Edition，2011，41（4）：939－943.（in Chinese）.

［8］刘元林，胡伍生，李素兰，等.基于投影寻踪神经网络模型的短时交通量预测研究［J］.交通信息与安全，2012，30（4）：44－47.Liu Yuanlin，Hu Wusheng，Li Sulan，et al.Shortterm traffic prediction based on a combined projection pursuit regression and BP neural network model［J］.Journal of Transport Information and Safety，2012，30（4）：44－47.（in Chinese）.

［9］Agrawal R，Faloutsos C.A Swami.Efficient similarity search in sequence database［C］∥Proceedings of the 4th International Conference of Foundation of Data Organization and Algorithms，Chicago，USA：University of Chicago，1993：69－84.

［10］Chan K P，Fu A W.Efficient time series matching by wavelets［C］∥Proceedings of the 15th IEEE International Conference on Data Engineering，Sydney，Australia：IEEE Computer Society 1999：126－133.

［11］Keogh E，Chakrabarti K，Pazzani M.Locally adaptive dimensionality reduction for indexing large time series databases［C］∥Proceedings of ACM SIGMOD Conference on Management of Data，SantaBarbara，Calif USA：University of California，2001：151－162.

［12］Lin J，Keogh E，Wei L.Experiencing SAX：a novel symbolic representation of time series［J］.Data Mining and Knowledge Discovery，2007，15（2）：107－144.

［13］Keogh E，Pazzani M.An indexing scheme for fast similarity search in large time series databases［C］.Proceedings of the 11th International Conference on Scientific and Statistical Database Management，Cleveland，Ohio，USA：Cleveland State University，1999：56－67.

［14］Perng C.S，Wang H，Zhang S，et al.Landmarks：a new model for similarity－based pattern querying in time series databases［C］∥Proceedings of the IEEE 16th International Conference on Data Engineering，San Diego，Calif，USA：IEEE Computer Society，2000：33－42.

［15］Jaeger H，Haas H.Harnessing nonlinearity：prediction of chaotic time series with neural networks［J］.Science，2004，304（5667）：78－80.

［16］彭 宇，王建民.彭喜元.基于回声状态网络的时间序列预测方法研究［J］.电子学报，2010，38（2A）：148－154.Peng Yu，Wang Jianmin，Peng Xiyuan.Research on time series prediction with echo state networks［J］.Acta Electronica Sinica，2010，38（2A）：148－154.（in Chinese）.