基于城市主干路交通流数据的跟驰模型标定＊

曹金亮 史忠科 房雅灵

（1.西北工业大学自动化学院 西安 710129；2.浙江海洋学院数理与信息学院 浙江 舟山 316022）

0 引言

为了解决城市交通拥堵、交通事故频发等问题，各国学者提出了各种各样的交通流模型［1－16］。车辆跟驰理论［4］是从微观上研究交通流的理论，它是运用动力学方法，研究在无法超车的情况下跟车的速度如何随着前车的速度变化而变化。处于跟驰状态的行驶车队，跟车的速度不能长时间大于或者小于前车的速度，只能在前车速度的某邻域内摆动。同时，前后两车必须保持一定的距离（称为安全距离），以避免发生碰撞。由于后车速度的变化滞后于前车，行驶车队可能呈现出时走时停的状态。跟驰模型即是通过分析每个跟随车辆的跟驰行为以理解交通流特性，在驾驶人的微观行为与交通流宏观现象之间建立起联系。它在微观交通仿真、通行能力分析、自适应巡航控制、交通安全评价等领域都有着很广泛的应用价值。城市主干路是城市道路交通网的骨架，是连接城市各主要分区的交通干道。由于受到各种交通条件的影响，比如上下游交叉口距离、信号周期时长、公交车停靠等情形的影响，交通流常表现为间断流，这使得交通流经常处于饱和（拥堵）或近饱和的状态，与高速公路和城市快速路的交通流特征有明显的区别。

一般地，跟驰模型的结构确立以后，需要通过模型标定和验证后才能具体应用到实际中。而国内外学者对跟驰行为的研究，大多侧重于对跟驰模型结构的研究，对跟驰模型的参数标定及效果验证的研究相对较少。Helbing等［6］提出了广义力模型，利用安装在车后的雷达系统测得的数据标定了该模型。Kesting等［7］利用Bosch GmbH数据集，运用遗传算法对IDM 模型和优化速度模型做了比较分析。我国学者王殿海等［8］标定了一个经典模型——GM 模型。但是，在笔者所收集到的资料当中，利用城市主干路交通数据对跟驰模型进行标定的文献尚属空白。

对跟驰模型进行标定和验证的前提是实际交通数据的获取。传统的交通数据获取方法主要采用基于虚拟线圈、虚拟线和虚拟点的方法。与传统方法相比，通过视频检测获取交通数据的方法具有图像监控和交通数据采集双重功能，还具有安装简单、成本低、运行方式灵活、无需埋设线圈、设备可在不同地点间移动等优势。笔者利用视频手段获取了西安市和舟山市的某个主干路路段的交通流实测数据，并根据这些数据对典型的交通流跟驰模型进行标定与验证，以此寻找更适合于主干路特性的跟驰模型，从而加深对城市主干路的交通流特性的认识，为缓解交通拥堵提供理论依据。

1 车辆跟驰模型简介

车辆跟驰模型大致有刺激－反应模型、安全距离模型、驾驶心理模型和基于人工智能的模型等。由于实测得到的数据为城市主干路的交通流数据，所以笔者选取其中更适于近饱和状态的惯性模型（inertial model，IM）［9］和智能驾驶人模型（intelligent driver model，IDM）［10－12］进行对比研究。

1.1 惯性模型

Tomer等在文献［9］中提出的惯性模型是1个不显含优化速度函数的跟驰模型。其数学表达如下。

式中：vn（t）和xn（t）分别为第n辆车在时刻t的速度和位移；xn－1（t）－xn（t）为车间距；A为敏感系数；T为安全时间间隔；D为最小安全车间距；k为常数；v0为允许速度。

式（1）中的第1项表示跟车速度很小时，若期望车间距vn（t）T＋D大于实际车间距xn－1（t）－xn（t）时，则跟车加速，否则，跟车需要减速；第2项表示跟车速度大于前车速度时，则跟车需要减速；第3项表示跟车的车速超过允许速度，则跟车需要减速。

1.2 智能驾驶员模型

Treiber，Helbing 和Kesting等提出了智能驾驶人模型［10－12］，试图用该模型统一描述从自由流到完全拥挤流的不同状态，模型具体形式如下。

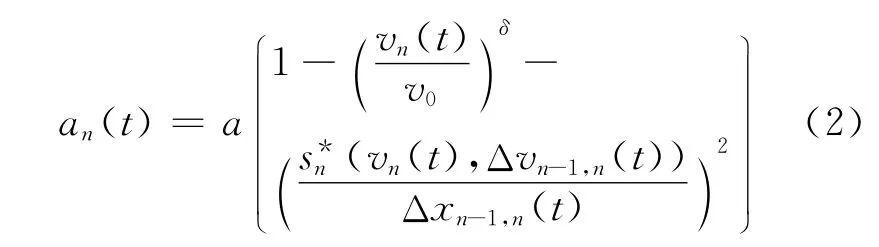
在IDM 中，当前车速度小于跟车速度，即Δvn－1，n（t）＜0 时，则需要1个较大的期望车间距。否则，允许接受1个较小的期望车间距。这正是模型中（vn（t），Δvn，n－1（t））的意义，它体现了智能驾驶的特点。当车间距很大时，IDM 退化成

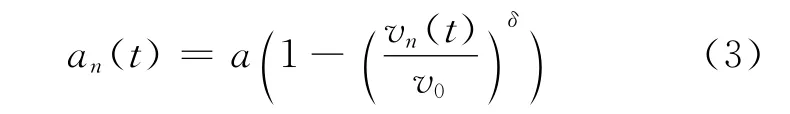
表示以加速度a开始加速度，直至达到理想速度。

2 数据的采集与处理

要使车辆跟驰模型能够应用于实际交通、再现交通现象，需要采集实际的交通流数据以确定车辆跟驰模型中的待定参数。为此，笔者对陕西省西安市太白立交桥附近二环路和浙江省舟山市昌洲大道的交通状况进行了长时间地跟踪观察。这2条道路均为双向3车道的城市主干路，其交通状况反映了城市的交通现状。为获取所需要的交通流数据，选择交通流变化较大的早高峰、中午和晚高峰的时段进行视频拍摄，并对所拍摄视频进行技术处理。

首先，将视频转换成图像。在拍摄的视频中选取画面清晰、车辆跟驰特征显著的视频（见图1），利用视频处理软件，按帧将视频转换成图像，选取在中间车道上的行驶车辆（即图1中所示的区域）来提取交通流数据。

图1 视频转换图像Fig.1 Image extracted from video

其次，将图像转换成俯视图。现实中远处车辆与近处车辆行驶了相同的距离，但是由于透视现象的存在，使得在图像中前者比后者要小。为此，须用反透视变换将实际图像转换成俯视图像以便准确反映车辆的实际位置。反透视变换的效果见图2。

图2 图像反透视变换效果图Fig.2 Inverse perspective transformation of image

最后，提取交通流数据。为了避免不同车种的车长差别的影响，笔者选取前车车尾与后车车头的实际位置来计算相关的交通流数据。先将视频的采样频率设定成30帧／s，然后按0.1s的时间间隔即每3帧提取前车车尾与后车车头的像素值，并按比例转换成它们的实际位置。由此可以得到每辆车的位移以及相邻2 车的车间距（前车车尾与后车车头的间距），再根据位移计算出每辆车的速度和加速度。

由于所选道路的允许速度为60～90km／h，即16.7～25 m／s，而在获取的交通流数据中，跟车的最大速度为6.2m／s，远小于允许速度，这表明交通流已处于近饱和状态。

3 模型的参数标定

3.1 标定原理

模型的参数标定是运用数学手段、结合相关数据，将模型中的待定参数具体化的过程［7］，它是交通流建模中不可缺少的步骤，只有经过标定的模型才可付诸应用。模型参数标定是通过对模型的输出结果与实测结果进行比较，建立1个能够反应与实际的贴合程度的评价指标，把参数标定问题转化成1个优化问题进行处理。

跟驰模型的一般形式可表示为

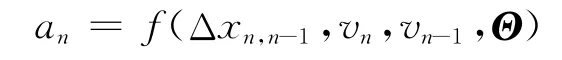
式中：Θ＝（θ1，θ2，…，θl）是待定的参数向量。

即跟车an的加速度是它与前车的车间距、跟车速度以及前车速度的函数。

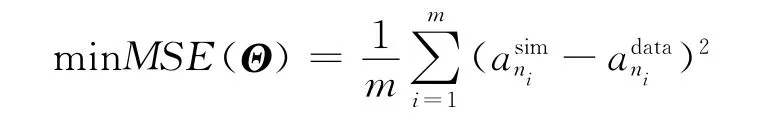
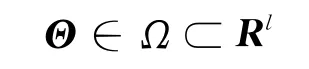
式中：MSE为均方误差；Ω为参数向量Θ的允许取值集合；Rl是l维实数空间。

下面利用城市主干路早高峰、中午和晚高峰的实测数据，采用Levnberg－Marquardt算法对惯性模型和智能驾驶员模型进行标定。

3.2 惯性模型的参数标定

在惯性模型中需要标定的参数有A，k，T，D，v0，即Θ＝（A，k，T，D，v0）。由式（1）可见，如果跟车速度vn（t）小于允许速度v0时，式（1）中的第三项恒等于零，此时k可以取任意数，否则k也需要标定。若允许速度v0＝20m／s，则v0＞6.2m／s，此时标定结果见表1，其中k可为任意常数；若允许速度v0＜6.2m／s时，标定结果见表2，此时，k的值会影响模型效果。可以看出，对于不同的数据，得到的参数变化是比较大的。

表1 IM 模型当vn＜v0时的标定结果Tab.1 Calibration results of IM when vn＜v0

表2 IM 模型当vn＞v0时的标定结果Tab.2 Calibration results of IM when vn＞v0

3.3 智能驾驶人模型的参数标定

在智能驾驶人模型中，需要标定的参数有v0，T，s0，a，b，即Θ＝（v0，T，s0，a，b）。若加速度指数选取与文献［8］的值，即δ＝4，则标定结果见表3。由表3可见，理想速度v0要么很大，要么很小，这与实际是不相符的。为此，让δ取不同的值对模型进行标定，得到的结果见表4～表6。从标定结果可见，当δ越来越大时，v0越来越接近给定的初始值20m／s。事实上，从模型的退化形式式（3）可以看出，当δ→∞时，车辆以恒定的加速度a加速到理想速度v0，表明标定结果与这一事实是相符的。

表3 IDM 当δ＝4时的标定结果Tab.3 Calibration results of IDM whenδ＝4

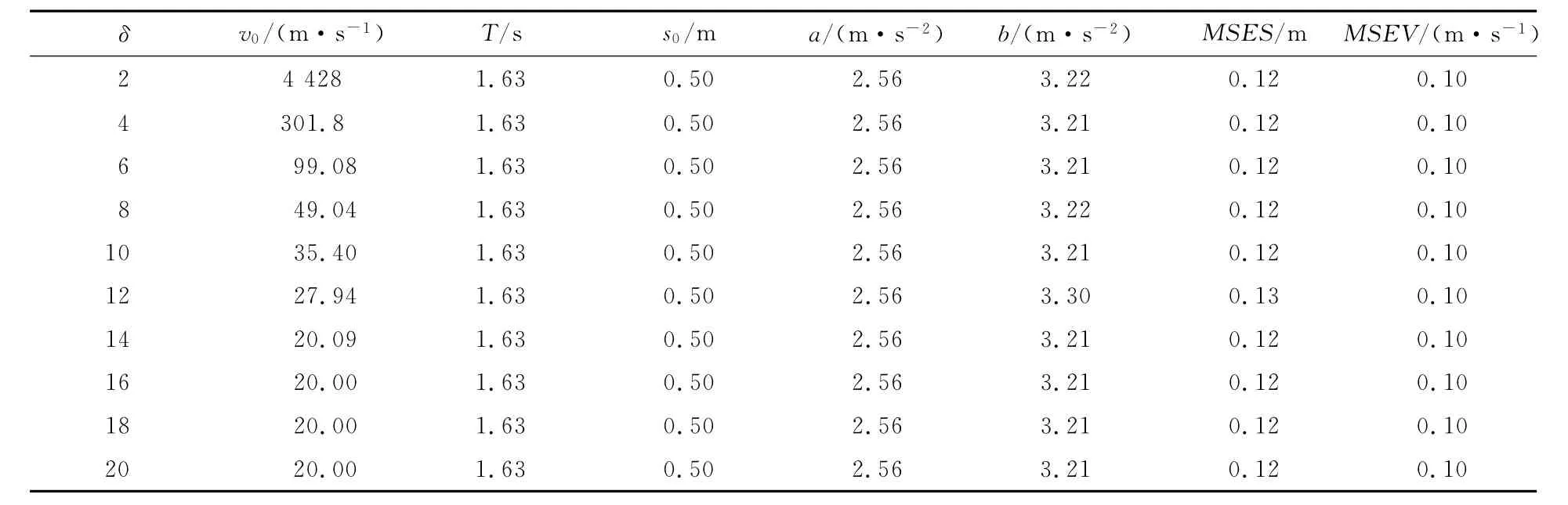
表4 基于早高峰数据δ取不同值的标定结果Tab.4 Calibration results of IDM for differentδbased on morning rush hour data

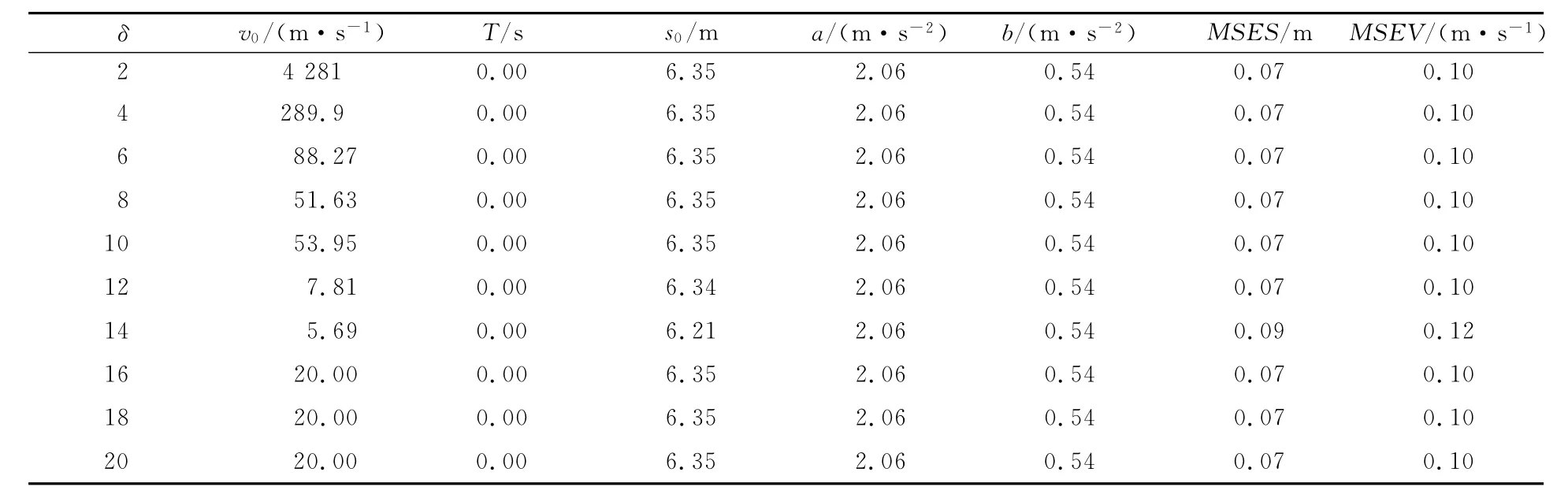
表5 基于中午数据δ取不同值的标定结果Tab.5 Calibration results of IDM for differentδbased on noon rush hour data

表6 基于晚高峰数据δ取不同值的标定结果Tab.6 Calibration results of IDM for differentδbased on evening rush hour data

4 模型评述与对比

第3节已经对允许速度大于和小于实际速度2种情况下的惯性模型进行了标定。对于前1种情况，利用3 组数据得到的位移均方差分别为0.41，2.37，5.61m，平均值为2.80m，速度均方差分别为0.11，0.75，0.89 m／s，平均值为0.58 m／s；对于后1种情况，位移均方差分别为0.11，0.94，5.61m，平均值为2.22m；速度均方差分别为0.11，0.47，0.89m／s，平均值为0.49m／s。数据显示，可以用惯性模型描述近饱和状态时的交通流。

就智能驾驶人模型而言，如果加速度指数取为4，按3 组数据计算出的理想速度分别为301.8，289.9 和5.81 m／s，这与实际情况不符。但是，随着加速度指数的增大，标定结果越来越符合实际。表明用智能驾驶人模型描述接近饱和状态时的交通流时，模型中的加速度指数需要选择比较大的值。

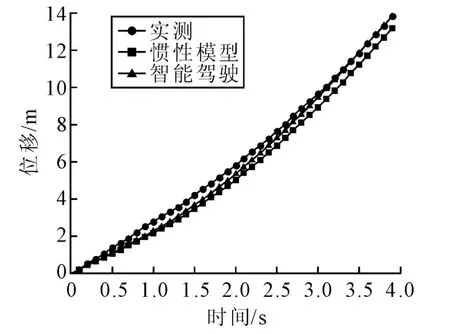
图3 早高峰的车辆实测与仿真位移曲线Fig.3 The real and numerical curve of the vehicle position based on morning rush hour

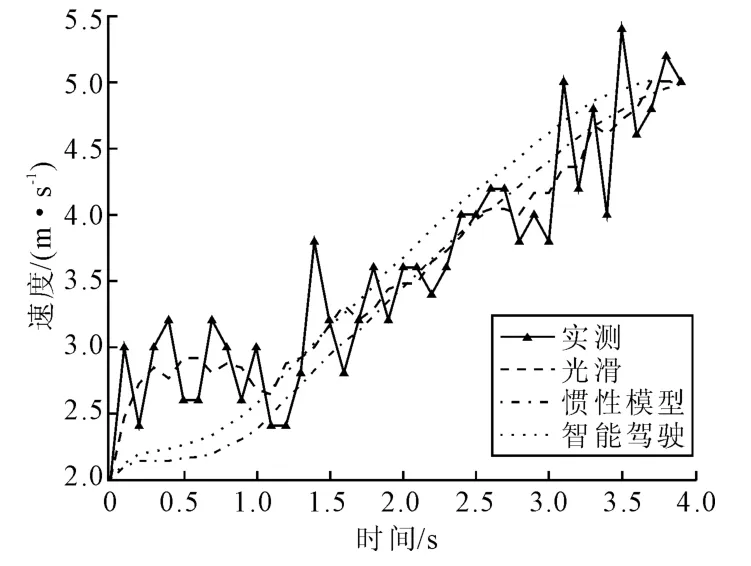
图4 早高峰的车辆实测与仿真速度曲线Fig.4 The real and numerical curve of the vehicle velocity based on morning rush hour

图3～图8 分别是3 组数据的实测、惯性模型仿真和智能驾驶人模型仿真的位移曲线和速度曲线。从这些图中，可以更直观地看出智能驾驶人模型更加符合本文的实测数据。虽然本文所测数据对于惯性模型和智能驾驶人模型都是适用的，但是对于同一组数据，比较惯性模型和智能驾驶人模型的2 个优化性能指标MSES和MSEV（见表1～表3），可以看出，智能驾驶人模型较惯性模型更适合于城市主干路近饱和状态时的车辆跟驰行为。

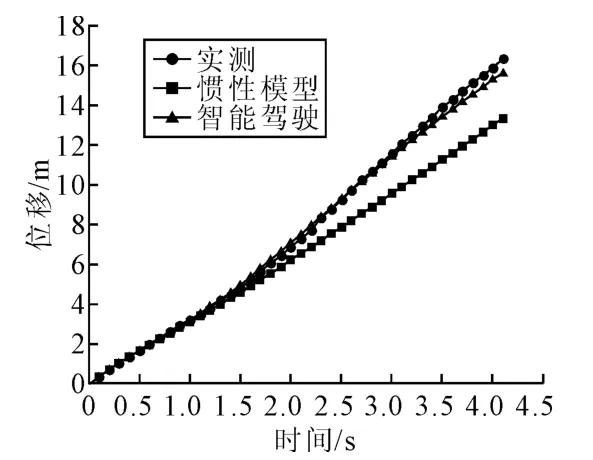
图5 中午的车辆实测与仿真位移曲线Fig.5 The real and numerical curve of the vehicle position based on noon rush hour

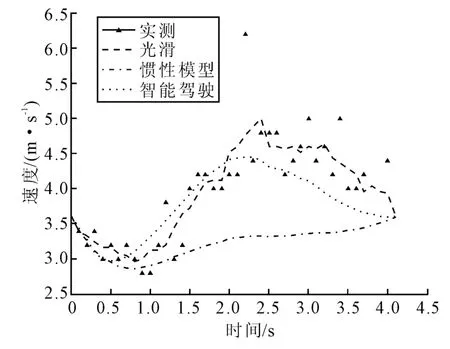
图6 中午的车辆实测与仿真速度曲线Fig.6 The real and numerical curve of the vehicle velocity based on noon rush hour

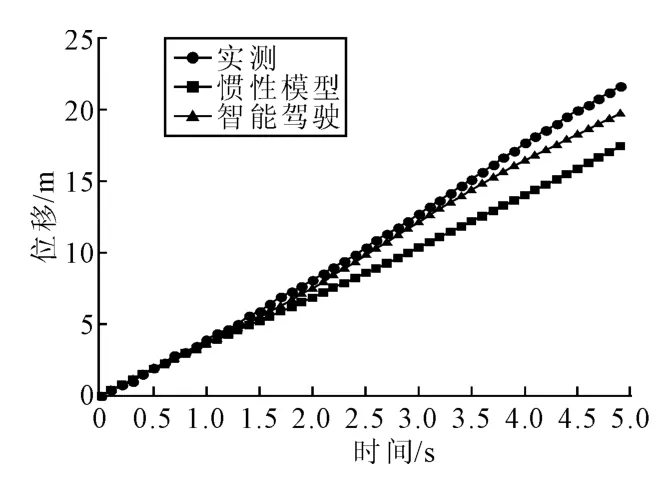
图7 晚高峰的车辆实测与仿真位移曲线Fig.7 The real and numerical curve of the vehicle position based on evening rush hour

5 结束语

笔者通过采集西安市二环主干路上和舟山市昌洲大道上典型时间段内车辆的微观运动录像，利用Matlab软件将视频处理成图像，提取出主干路接近饱和状态下车辆微观运动的轨迹数据。根据采集数据的特点，选取不显含优化速度函数的2个典型的车辆跟驰模型即惯性模型和智能驾驶人模型进行了标定和验证。

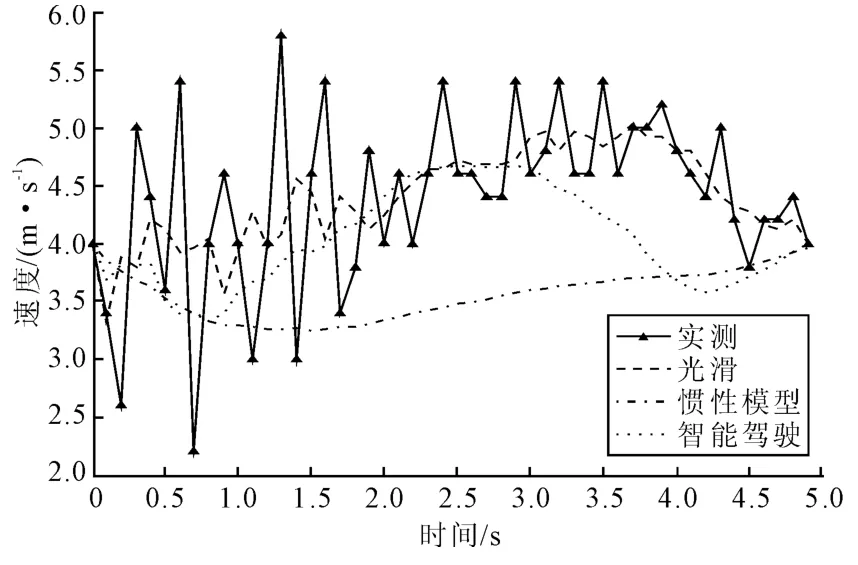
图8 晚高峰的车辆实测与仿真速度曲线Fig.8 The real and numerical curve of the vehicle velocity based on evening rush hour

选用模型输出与实测数据的均方误差作为优化性能指标，利用Levnberg－Marquardt算法对3组实测数据分别得到2个模型的标定结果。首先对允许速度大于和小于实际速度2种情况下的惯性模型进行了标定。结果表明，可以用惯性模型描述接近饱和状态时的交通流。对于智能驾驶人模型，如果加速度指数值较小，则理想速度与实际不符。随着加速度指数的增大，标定结果越来越符合实际。因此，用智能驾驶人模型描述接近饱和状态时的交通流时，加速度指数要选择比较大的值。比较惯性模型和智能驾驶人模型的优化性能指标，可以得出，智能驾驶人模型较惯性模型更适合于城市主干路接近饱和状态时的车辆跟驰行为。它在理论上为缓解交通拥堵提供了一定的思路和方法。

［1］Bando M，Hasebe K，Nakayama A，et al.Dynamical model of traffic congestion and numerical simulation［J］.Physical Review E，1995，51（2）：1035－1042.

［2］Zhou J，Shi Z K，Cao J L.Nonlinear analysis of the optimal velocity difference model with reactiontime delay［J］.Physica A：Statistical Mechanics and its Applications，2014，396（2）：77－87.

［3］Zhou J，Shi Z K，Cao J L.An extended traffic flow model on a gradient highway with the consideration of the relative velocity［J］.Nonlinear Dynamics，2014，396（2）：1－15.

［4］Brackstone M，Mcdonald M.Car－following：a historical review［J］.Transportation Research Part F：Traffic Psychology and Behaviour，1999，2（4）：181－196.

［5］Newell G F.A simplified car－following theory：a lower order model［J］.Transportation Research Part B：Methodoloical，2002，36（3）：195－205.

［6］Helbing D，Tilch B.Generalized force model of traffic dynamics［J］.Physical Review E，1998，58（1）：133－138.

［7］Kesting A，Treiber M.Calibrating car－following models by using trajectory data：Methodological study［J］.Transportation Research Record：Journal of the Transportation Research Board，2008，2088（1）：148－156.

［8］王殿海，陶鹏飞，金 盛，等.跟驰模型参数标定及验证方法［J］，吉林大学学报：工学版，2011，4（S1）：59－65.Wang Dianhai，Tao Pengfei，Jin Sheng，et al.Method of calibrating and validating car－folling model［J］.Journal of Jilin University：Engineering and Technologh Edition，2011，41（S1）：59－65，（in Chinese）.

［9］Tonmer E，Safonov L，Havlin S.Presence of many stable nonhomogeneous states in an inertial carfollowing model［J］.Physical Review Letters，2000，84（2）：382－385.

［10］Treber M，Hennecke A，Helbing D.Congested traffic states in empirical observations and microscopic simulations［J］.Physical Review E，2000，62（2）：1805－1824.

［11］Treber M，Helbing D.Memory effects in microscopic traffic models and wide scattering in flow density data［J］.Physical Review E，2003，68（4）：1－8.

［12］Treiber M，Kesting A，Helbing D.Delays，in accuracies and anticipation in microscopic traffic models［J］.Phyica.A：Statistical Mechanics and its Applications，2006，360（1）：71－88.

［13］Chen J，Shi Z，Hu Y，et al.An extended macroscopic model for traffic flow on a highway with slopes［J］.International Journal of Modern Physics C，2013，24（9）：1－4.

［14］Yu L，Shi Z，Li T.A new car－following model with two delays［J］.Physics Letters A，2014，378（4）：348－357.

［15］熊 惠，孙小端，贺玉龙，等.高速公路运行速度与交通安全关系研究［J］.交通信息与安全，2012，30（6）：48－51.Xiong Hui，Sun Xiaoduan，He Yulang，et al.Relating the operating speed and traffic safety on freeways［J］.Journal of Transport Information and Safety，2012，30（6）：48－51.（in Chinese）.

［16］漆巍巍，裴玉龙.城市道路拥堵状态下驾驶人心率特性研究［J］.交通信息与安全，2014，32（3）：18－21.Qi Weiwei，Pei Yulong.Characteristics research for driver’s heart rate in congerstion state of urban road［J］.Journal of Transport Information and Safety.，2014，32（3）：18－21.（in Chinese）.