基于R 树的非参数回归交通流预测方法

余沁潇 凌 帅 吴 刚，2 马寿峰▲

（1.天津大学管理与经济学部 天津 300072；2.天津高速公路集团有限公司 天津 300384）

0 引言

随着智能交通系统的发展，交通管理模式逐渐由被动转为主动，短时交通流预测作为智能交通系统的核心技术之一，为交通信息服务、交通控制与诱导提供基础数据，对预测效率和精度都要求较高。短时交通流预测的研究方法可分为2类：传统的基于数学模型的方法；数据驱动式的计算智能方法［1］。近年来，面对复杂的路况以及大量的交通数据集，第1类方法存在明显不足，学者们逐渐将研究重点转向后者［2－5］。非参数回归预测就是1种基于数据驱动式的计算智能方法，它实际上是基于模式匹配和数据挖掘的方法，其优点在于它完全是数据驱动的，几乎不需要先验知识，只需要有足够规模的模式库，就可以做到比较准确的预测。

近年来，许多学者将非参数回归方法应用于交通流预测，但在实际应用中存在预测时间长，实时性差的缺陷。1991 年，Davis和Nihan［6］首次将非参数回归的方法应用于交通预测中，指出该方法适用于预测非线性的交通数据，但该算法需要维护1个庞大且具有代表性的历史数据库，因此运行所耗费的时间相对较长。Smith等［7］将非参数回归模型应用于单点短时交通流预测，但在实际使用上仍存在搜索速度过慢的问题。后来，许多学者就这一问题提出解决方案，Oswald等［8］用KD 树来建立历史模式库进行模糊最近邻搜索，缩短了K 近邻算法的运行时间。张晓利等［9］针对非参数回归中案例库生成难和搜索速度慢的问题，提出1种基于平衡二叉树的K－邻域非参数回归预测方法，该算法首先对历史数据进行聚类，然后采用平衡二叉树建立历史数据库，预测速度有一定提高。贾宁等［10］用KD 树作为模式库的存储结构，并基于KD 树进行最近邻搜索，有效地提高了近邻搜索速度。但KD 树的形态高度依赖于数据的插入顺序，不合理的插入顺序会影响KD 树的结构，从而影响查询效率。另外，数据的删除会导致KD 树结点的重新组织，而现实中预测系统不断增加新数据，剔除旧数据，这使得模式库的更新耗费大量时间［11］。

综上所述，非参数回归方法可以解决交通流预测中的非线性和不确定性问题，使预测精度达到满意的效果。但该方法要求大量的历史数据来构建历史模式库，当数据量和状态向量维数增长时，预测的速度将下降，从而影响预测的实时性。随着大数据时代的到来，交通流数据不断增长，同时为了准确预测交通流量，考虑的影响因素也越来越多，如检测点历史流量、速度、占有率，上下游的流量、速度、占有率，信号灯情况，天气因素，地理位置等。这些问题使得非参回归方法中历史模式数据库建立和模式搜索的速度受到挑战，而传统的线性数据库已经不能满足预测的实时性要求。因此，笔者提出了1种基于R 树的K 近邻非参数回归短时交通流预测方法，该方法使用R 树来建立模式库，根据数据在空间中的分布进行存储，使相近数据存储在同1个或相邻的节点中，这便使得K 近邻搜索的速度得以提高，从而提高预测的实时性。

1 基于R 树的交通流非参数回归预测方法

1.1 交通流非参数回归预测方法

非参数回归是1种数据驱动的预测技术，是1种适合于不确定性和非线性性动态系统的非参数估计方法。将其用到交通流预测中的主要过程就是在数据库中寻找与当前交通模式相近的历史模式，再用这些历史模式去预测当前交通流量。在数据库中，1条交通流模式由2部分组成，一部分为断面交通流的状态向量，即影响该断面交通流量的因素f1～fn，如该断面以及上下游的历史交通流特征（流量、速度、占有率）、天气、地理位置等；另一部分则为断面的交通流量q，它由状态向量所决定。因此，1 条交通流模式可表示为｛f1（ti），…，fn（ti）｜q（ti）｝。随着交通系统的运行，交通流模式将不断被加入到历史模式数据库中。

1.2 R树结构

R 树［12］最初由Guttman于1984年提出，作为1种空间索引机制，它将空间对象按范围划分，每个结点对应1个空间区域，在物理存储上，每个结点对应1个磁盘页。相应于交通流数据，由于它的状态向量往往都是多维的，因此1条交通流模式可被看作是多维空间中的1个点，那些状态向量相似的模式在多维空间中是相邻的，它们将被划分到同1个字空间存入同1个磁盘页。因此在进行数据检索时，可根据数据的空间位置快速有效地在多维空间中找到1组相似的数据。R 树中的结点分为2种：叶结点和非叶结点，叶结点存储的是其区域范围内所有空间对象的最小边界矩形（minimum bounding rectangle，MBR），非叶结点存储的是包络其所有子结点所在空间范围的MBR。该设计使得对空间对象进行搜索时只需访问小部分结点，并且可以方便快速地进行空间对象的插入和删除操作，无需对树中所有数据进行空间上的再组织。

R 树空间数据存储方法是把多维空间进行递归划分，最终将空间对象划分到不同的子空间中。每个子空间都由1个结点表示，而每个结点有惟一的记录形式。叶结点的记录形式为：（M，i）。其中：M为包络了该结点中所有空间对象的MBR；i为该结点的标识即其物理存储地址。非叶结点的记录形式为：（M，p）。其中：M为包络了其所有子结点所在区域的MBR；p为指向其子结点存储位置的指针。对于n维空间中的1 个MBR，M可表示为M＝（I0，I1，…，In－1），其中：Ii指空间对象在第i维上的取值范围［a，b］，它在数值上等于该空间中所有数据第i维的最小值和最大值。

R 树的构造方法就是将数据点逐个插入到R树中，在插入过程中，寻找最优的路径，使相近数据聚集在同1 个结点中，保证R 树的结构稳定。下面给出R 树构造的伪代码，设R 为R 树的根结点，E为要存入到R 树中的数据。

1.3 基于R 树的K 近邻搜索策略

历史模式数据库中交通流模式的状态向量是多维的，而且模式数量众多，R 树组织结构的特点就是将空间中相邻的对象划分在1个区域内，使它们拥有共同的祖先，待测对象与其他对象间的距离可以通过它们的祖先与待测对象的距离表示。使用R 树进行近邻搜索，可通过祖先与待测对象的距离剔除大部分距离远的分支，这样便可提高查找效率。

R 树中结点存储的是其若干子结点或空间对象的MBR，MBR 为包络对象所在空间的最小边界矩形，通常用其主对角线上的2个顶点表示，例如，在二维空间里，用（xl，xh，yl，yh）表示。在本文中，用minDist表示点p到空间内某矩形R的最小距离，若点p在矩形R内，则两者距离为零；若点p在矩形R外，则两者的距离为p到矩形R上最近1点的欧式距离平方值。则minDist（p，R）表示为［13］

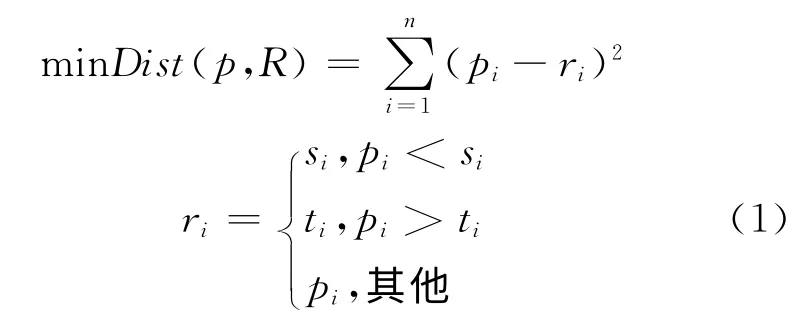
式中：pi为n维待测点p第i维的值，i＝1，2，…，n；ri为n维空间矩形R在第i维与待测点p距离较近的值，i＝1，2，…，n；si为n维空间矩形R在第i维上的最小值。ti为n维空间矩形R在第i维上的最大值。

可以证明，点p到MBR的minDist小于等于点p到该MBR中任意对象O的距离［14］。因此minDist值可以看作待测点p到每1个MBR中对象的距离下限，在查找过程中可以按照minDist值从小到大排列，确定MBR的搜索顺序，从而减少需要访问结点的数量。但因为MBR内对象分布不均匀，待测点到MBR中对象的距离比minDist确定的距离远，如果先访问minDist值小的MBR，并将其中的对象都作为近邻点，那么将损失更优的对象，从而影响了预测精度。如图1 所 示，minDist（p，MBR1）＜minDist（p，MBR2），但MBR2中的对象多集中于靠近点p一侧，而MBR1中的对象多集中于远离点p的一侧。因此，点p到MBR2中对象的距离比到MBR1中对象的距离小，若将MBR1中的对象均视为p的近邻，则会影响预测精度。为解决该问题，引入参数距离上限r，它表示近邻点与待测点之间的距离上限，若MBR中的对象到p的距离小于r，则将其视为近邻点。因此，即使某个MBR到待测点p的minDist较小，若其中的对象到p的距离都大于r，舍弃该MBR，继续搜索其它的MBR，直到搜索到K个近邻或者遍历完整棵树。

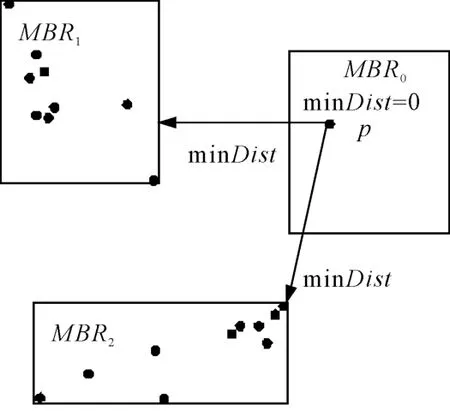
图1 minDist示意图Fig.1 minDist

因此笔者采用的K 近邻搜索策略是：首先设定1个距离上限r，对于MBR中的任意对象O，当Dist（p，O）≤r时，将其视为p的近邻；然后对R 树进行有序深度优先遍历，从根结点开始向下逐层访问MBR，对于同层的结点，计算所有MBR到待测点p的minDist，然后将结点按minDist由小到大排序后放入链表ABL中；之后选择minDist最小的结点递归进行以上过程，直至到达叶结点，在叶结点中选择距离小于r的对象放入近邻集合中；若近邻个数等于K或遍历完整棵树，则搜索完成，否则，返回链表中ABL搜索下一个结点。

设R 树的根节点为R，待测点为p，搜索的距离上限为r，近邻个数为K，近邻点存于Nearest列表中。则该搜索策略的伪代码如下：

1.4 预测算法

预测算法是影响预测精度的重要因素，它是根据K 近邻查找得到的近邻点，利用预测函数做出合理的预测。

笔者采用带权重的预测方法，设搜索到的K个近邻点为n1，n2，…，nk，对应的决策属性为y1（t＋1），…，yk（t＋1），待测点与第i个近邻点的距离为di（i＝1，2，…，k），距离越小的点在预测中所占的权重越大，则预测算法如下。

2 实验与应用

2.1 线性和R 树结构下K 近邻搜索速度的对比

首先针对2 种结构下的历史模式库进行K近邻搜索速度的比较实验。在实验中，每个数据对象由10维状态向量表示，状态向量中的各分量是随机生成的0～1 之间的实数，距离上限r为1，近邻个数K＝20。对不同规模的模式库进行查找实验。实验程序使用Java语言编写，硬件环境为2.4GCPU，4G 内存，实验结果见图2。

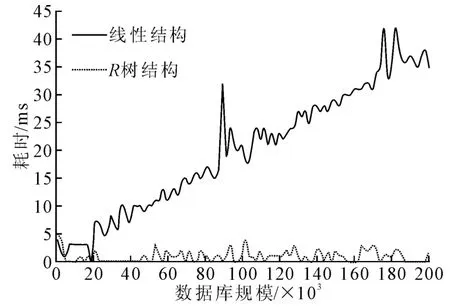
图2 R 树结构与线性结构的搜索速度对比Fig.2 The comparison of searching performances under the R－tree and linear structure

由图2可见，随着数据规模的增大，线性结构的查找耗时增长快，而R 树结构查找速度比较稳定，在耗时上没有明显的增长。这是因为在线性结构的数据库中进行K 近邻查找时，需要遍历整个数据库，进行1次最近邻搜索的时间复杂度是O（kN），k是数据对象的维数，N是数据库规模，因此查找时间与数据库规模N成正比。R 树的查找速度与其遍历的节点数目以及每个节点中数据对象的数量成正比，而其遍历的节点数目与R树的高度有关，R 树的高度可表示为，因此R 树最近邻查找的时间复杂度可表示为O（k·，式中：k为数据对象的维数；N为数据库规模；m为节点容量下限。因此使用R 树进行K 近邻查找的速度明显优于线性结构。

2.2 预测应用

2.2.1 数据来源

实验采用的交通数据来自加利福尼亚州交通局的路况监测系统［15］（caltrans performance measurement system），这些数据采集自圣地亚哥市I5号公路由北向南24.4km（15.2 mile）处的检测器，包含了2013年1月1日～2014年1 月15日的流量数据，其中每5min记录1条交通流量，1d共288个样本。实验中将所有样本的交通流量进行归一化处理，以2013年全年105 120条数据作为历史模式来建立数据库，2014 年的4 320条数据作为测试数据来进行流量预测，预测周期为5 min。在预测中，仅考虑交通流量之间的时间关联，用前10个时刻的流量来预测本时刻的流量。

2.2.2 近邻个数和距离上限的确定

在本文涉及的K 近邻搜索策略中，对最后预测精度及速度起到影响作用的参数有2 个，1 个是近邻个数K，另1个是距离上限r。对于近邻个数K而言，过大或过小都会影响非参数回归预测结果，如果K过大，那么需要搜索较多的结点，增加搜索耗时。如果K过小，则会降低预测精度。通过对比实验检验K值与预测误差的关系，其他参数固定，K分别取不同的值进行预测，预测效果见图3，当K值为20时，预测结果的平均相对误差最小，因此实验中K值取20。

图3 近邻个数K 与平均相对误差关系Fig.3 The relationship between the number of neighbors and average relative error

对于距离上限r来说，如果r过大将起不到约束minDist的作用，虽然在进行K 近邻查找时，能较快找到K个近邻，但这些近邻与待测点的距离却相对较远，即这些点并不是待测点的最优匹配点，在未访问的结点中可能存在与待测点更加匹配的数据。这样虽然达到一定的预测效率，却在预测精度上略有不足。如果r过小，即对待测点的近邻要求更严格，这样在近邻查找过程中将访问更多的结点来查找最优近邻，虽然提高预测精度，但是却以牺牲预测效率为代价。图4是不同r值与耗时的关系图，在实验中，从0 开始，每隔0.01 取1 个r值，直到r为1。每 个r值，进行20次K 近邻查找，其中K＝20，再计算平均耗时，结果如图4所示，当距离上限r从0增到0.05时，耗时显著减小，当距离上限r继续增大时，耗时渐趋平稳。

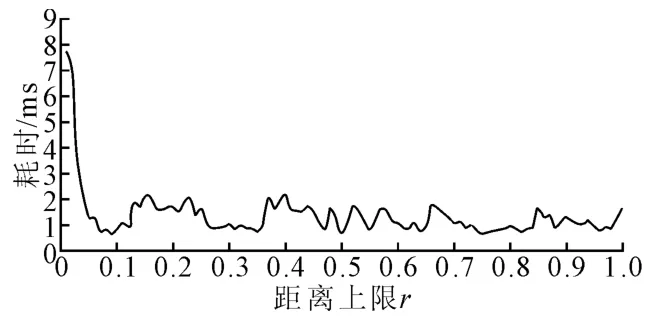
图4 r值与耗时的关系Fig.4 The relationship between r and time－consuming

2.2.3 预测结果

非参数回归是通过历史数据对未来数据的模拟，方法自身具有一定误差。线性结构下的非参数回归下的K近邻搜索，在遍历完所有的模式的前提下，找出K个近邻点，所得近邻点是距离待测点的最近的前K个，因此，它的误差可以看作是非参数回归方法自身的误差。表1为线性结构下，近邻个数为20时的预测结果。

表1 线性结构下的预测误差及耗时Tab.1 Average relative error and time－consuming based on linear structure

R 树结构下的非参数回归，除了非参数回归自身的误差之外，还应考虑R 树下K近邻查找的误差，该方法查找出来的K个近邻点，并不是离待测点最近的K个近邻，因此预测误差较大。但是在该方法中，误差的大小在一定程度上可以通过距离上限r调节。如表2所示，随着距离上限r减小，预测耗时不断增加，但都低于线性结构下的预测耗时，而平均相对误差不断减小，接近甚至优于线性结构下的预测误差。这是因为R 树的K近邻查找算法中共有2个参数来约束近邻点，当r值较大时，它对近邻点的约束条件放宽，更多的邻居点被当作近邻点，此时近邻个数K起到约束作用，即从多于K个的近邻点中选出前K个与待测点最相似的近邻点；当r值较小时，越来越少的邻居点符合近邻点的要求，此时存在少数待测点的近邻个数少于K，但这些近邻点与待测点的相似度更高，因此误差相对减小。

在表2中，当距离上限大于等于0.02 时，R树搜索到的平均近邻个数为20个，此时线性结构下搜索到的20个近邻相对更精确，因此线性结构下的预测误差总是小于R 树结构下的预测误差.但是在预测速度上，R 树结构下的搜索耗时远小于表1中线性结构下的搜索耗时。当距离上限为0.02时，R 树结构下的预测误差比线性结构的预测误差上升了8.8%，但预测速度提高了59.6%。当距离上限小于0.02时，R 树搜索到的平均近邻个数都小于20，与平均近邻个数为20的线性结构预测结果缺乏可比性，因此，为线性结构下的K近邻查找算法添加距离上限这一相同约束，其预测结果如表3所示，与表1结果比较，平均相对误差增大，这是因为对于大多数待测点来说，模式库中存在多余20个的近邻点，在考虑距离上限这一约束后，只要满足约束条件即可视为近邻点，无需遍历完所有模式，从而这些近邻点与待测点的相似度变小，因此预测误差增大，预测耗时减小。由表2与表3的对比结果显示，2种结构下搜索到的近邻个数相等且都小于20，在同一水平的距离上限下，R 树凭借自身的空间聚类特征，可以更快且更准确地找到满足条件的近邻，因此，R 树结构下的预测精度和速度都优于线性结构下的预测结果。

表2 R 树结构下不同距离上限r的预测结果Tab.2 The predicting result under different distance limits r based on R－tree

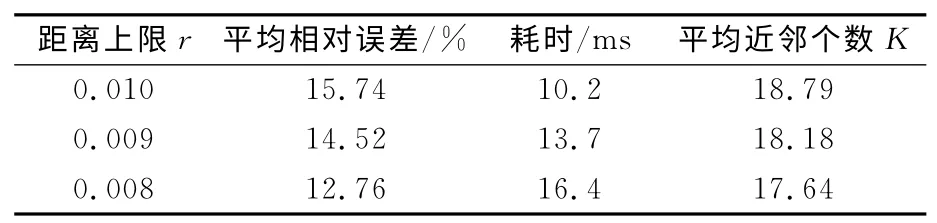
表3 线性结构下不同距离上限r的预测误差及耗时Tab.3 The predicting result under different distance limits r based on linear structure

3 结束语

交通流影响因素众多、交通数据海量增长，这2个因素分别导致非参数回归中的状态向量维数增长、历史模式库规模扩大，最终影响非参数回归的预测速度，尤其在短时交通流预测中，不能满足预测实时性的要求。因此，笔者提出1种基于R树索引结构的非参数回归短时交通流预测方法，使用R 树建立空间高维模式库，并依据R 树的空间聚类特点使用K 近邻搜索算法。实验结果显示这一方法在预测精度达到要求的前提下，能够大幅度地提高预测速度，即使模式库规模不断扩大，预测耗时的增长是缓慢稳定的，这为实现大规模路网下的交通诱导和控制提供了1种方法。

［1］贺国光，李 宇，马寿峰.基于数学模型的短时交通流预测方法探讨［J］.系统工程理论与实践，2000，12（11）：51－56.He Guoguang，Li Yu，Ma Shoufeng.Discussion on short－term traffic flow forecasting methods based on mathematical models［J］.Systems Engineering－theory＆Practice，2000，12（11）：51－56.（in Chinese）

［2］Karlaftis M G，Vlahogianni E I.Statistical methods versus neural networks in transportation research：Differences，similarities and some insights［J］.Transportation Research Part C：Emerging Technologies，2011，19（3）：387－399.

［3］刘 洋，马寿峰.基于聚类分析的非参数回归短时交通流预测方法［J］.交通信息与安全，2013，31（2）：27－32.Liu Yang，Ma Shoufeng.Non－parametric Regression for Short－term Traffic Flow Forecasting Based on Cluster Analysis［J］.Journal of Transport Information and Safety，2013（2）：27－32.（in Chinese）.

［4］Vlahogianni E I，Karlaftis M G，Golias J C.Short－term traffic forecasting：Where we are and where we’re going［J］.Transportation Research Part C：Emerging Technologies，2014，43（1）：3－19.

［5］徐华文，魏志强.基于数据流集成回归的短时交通流预测［J］.交通信息与安全，2014，32（4）：14－19.Xue Huawen，Wei Zhiqiang.An Online Shortterm Traffic Flow Prediction Model Based on Data Stream Ensemble Regression［J］.Journal of Transport Information and Safety，2014（4）：14－19.（in Chinese）.

［6］Davis G A，Nihan N L.Nonparametric regression and short－term freeway traffic forecasting［J］.Journal of Transportation Engineering，1991，117（2）：178－188.

［7］Smith B L，Demetsky M J.Traffic flow forecasting：Comparison of modeling approaches［J］.Journal of Transportation Engineering，1997，123（4）：261－266.

［8］Oswald R K，Scherer W T，Smith B L.Traffic flow forecasting using approximate nearest neighbor nonparametric regression［R］.Final Project of ITS Center Project：Traffic Forecasting：Non－parametric Regressions，Berkeley，CA：UC Berkeley Transportation library，2000.

［9］张晓利，贺国光，陆化普.基于K－邻域非参数回归短时交通流预测方法［J］.系统工程学报，2009，24（2）：178－183.Zhang Xiaoli，He Guoguang，Lu Huapu.Shortterm traffic flow forecasting based on K－nearest neighbors non－parametric regression［J］.Journal of Systems Engineering，2009，24（2）：178－183.（in Chinese）.

［10］贾 宁，马寿峰，钟石泉.基于遗传算法优化和KD树的交通流非参数回归预测方法［J］.控制与决策，2012，27（7）：991－996.Jia Ning，Ma Shoufeng，Zhong Shiquan.Nonparameter－regression traffic flow forecast method based on KD－tree and genetic optimization［J］.Control and Decision，2012，27（7）：991－996.（in Chinese）.

［11］Bentley J L.Multidimensional binary search trees used for associative searching［J］.Communications of the ACM，1975，18（9）：509－517.

［12］Guttman A.R－trees：A dynamic index structure for spatial searching［J］.ACM，1984，14（2）：47－57.

［13］Papadopoulos A，Manolopoulos Y.Performance of nearest neighbor queries in R－trees［C］∥Database Theory－ICDT′97.Springer Berlin Heidelberg，Delphi，Greece：Trier University，1997：394－408.

［14］Roussopoulos N，Kelley S，Vincent F.Nearest neighbor queries［J］.ACM Sigmod Record，ACM，1995，24（2）：71－79.

［15］PeMS.Caltrans Performance Measurement System［EB／OL］.（2014－01－16）［2014－01－30］http：／／pems.dot.ca.gov／，2014.