基于遗传算法和互信息公式结合的特征选择

涂昌慧，葛 红 ，胡天亮

(华南师范大学计算机学院，广州510631)

特征选择是统计学、机器学习和数据挖掘等领域中的经典问题. 在模式识别中，它根据一些准则，在删除一组不相关、冗余的特征后，选出对分类最有效的特征以达到降低特征空间维数，使得如分类、回归模型等任务达到和特征选择前近似甚至更好的预测精度［1］.

特征选择方法大致可以分为封装式(Wrapper)、过滤式(Filter)和嵌入式(Embedded)等3 类.封装式特征选择方法准确率较高，但容易出现过拟合现象，鲁棒性较差，依赖具体的学习算法，不适合大规模数据集［2］.过滤式特征选择方法的评估依赖于数据集本身，其可扩展性、鲁棒性高，适合大规模数据集［3］，但没有考虑与学习算法间的关系，得到的子集性能较差，嵌入式特征选择方法运行速度较快，选择的特征与分类性能有关，但其依赖于学习算法的选择，鲁棒性不高.

遗传算法是一种自适应的全局搜索方法，具有并行性和适合于解决多目标优化等特性. 互信息是2个随机变量统计相关性的测度.在特征选择中，互信息度量特征与类别标签的相关性是一种基于相关性的过滤式特征选择方法. 为了充分利用遗传算法和互信息的优点，本文结合遗传算法和互信息进行特征选择.

1 相关概念

1.1 遗传算法

遗传算法(Genetic Algorithm，GA)是一种通过模拟自然进化过程搜索最优解的方法. 其基本思想是从任意初始群体出发，通过随机选择、交叉和变异操作，产生一群更适应环境的个体.

遗传算法首先需实现从表现型到基因型的映射，即编码.初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生更好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于遗传算子进行组合交叉和变异，产生出代表新解集的种群.遗传算法在进化搜索过程中仅以适应度函数为依据，所以适应度函数直接影响到遗传算法的收敛速度以及能否找到最优解［4］. 遗传算法的3个基本操作:

(1)选择.根据个体的适应度值，按照一定的规则或方法，从上一代群体中选择出一些优良的个体遗传到下一代种群中. 选择的依据是适应性强的个体为下一代贡献一个或多个后代的概率大.

(2)交叉.交叉是把2个父个体的部分结构加以替换而生成新个体的操作.交叉操作产生的新一代个体，既保留了双亲的部分基因，又引入新的基因.

(3)变异. 变异可以防止求解过程中过早收敛产生局部最优解而非总体最优解.其操作为:对种群中的每个个体，以变异概率改变某一个或多个基因座上的基因值.变异本身是一种局部随机搜索，与选择算子结合在一起，保证了遗传算法的有效性，使遗传算法具有局部的随机搜索能力，同时保持种群的多样性，防止出现非成熟收敛.

1.2 互信息

互信息(Mutual Information，MI)是信息论中的一个基本概念.它表示2个变量间共同拥有信息的含量.系统的不确定性或复杂性可以用信息熵来描述.对于一个随机变量集X，其中任一xX，其概率分布函数用PX(x)表示，则集合X 的熵H(X)定义如下:

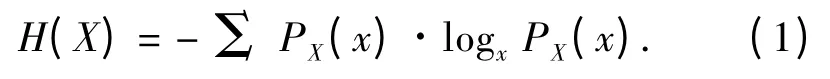
如果系统越有序，它的不确定性就越小，即熵值也越小，所含的确定信息越大.

给定2个随机变量集X 和Y，其条件熵分别定义:

随机变量集X 和Y 间的统计相关性可以用联合熵来描述，其定义:

其中，H(X)表示Y 未知时的熵，即X 的不确定性;H(X|Y)表示已知Y 后X 的不确定性，那么在知道Y后X 的不确定性减少量为H(X)－H(X|Y).这个不确定性的减少量即为互信息，它反映了Y 包含X 中信息的多少，可以描述为:

对于2个离散的随机变量X 和Y 还可以用2个变量的联合概率密度分布PXY(x，y)与2个变量完全独立时的联合概率分布PX(x)·PY(y)来表示互信息:

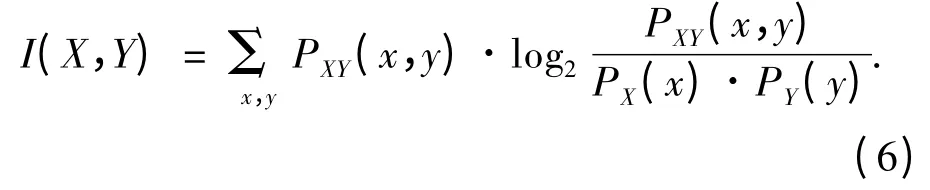
由定义可知，当变量X 和Y 完全无关或相互独立时，它们的互信息为0，说明它们之间不存在相同的信息;反之，当互信息值越大，它们间的相互依赖度越高，包含的相同信息也越多.

条件互信息是指在给定某个随机变量的条件下，其他2个变量之间的相互依赖程度.假如随机变量Z 已知，那么变量X 和Y 关于Z 的条件互信息为:

其中PXYZ(x，y，z)为联合概率分布，P(x|z)、P(y|z)和P(x，y|z)均为条件概率分布.

1.3 BP 神经网络

BP 神经网络是一种多层前馈神经网络，该网络的主要特点是信号向前传递的，而误差反向传播.在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层.如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络的权值和阈值，从而使BP 神经网络预测输出不断逼近期望输出. 由于BP 神经网络包含多个隐含层，故其具备处理线性不可分问题的能力.

1.4 概率神经网络

网络概率神经网络(Probabilistic Neural Networks，PNN)是一种径向基神经网络，在RBF 网络的基础上，融合了密度函数估计和贝叶斯决策理论.概率神经网络结构简单，能用线性学习算法实现非线性学习算法的功能［5］.PNN 不像传统的多层前向网络那样需要用BP 算法进行反向误差传播的计算，而是完全前向的计算过程.在某些易满足的条件下，以PNN 实现的判别边界渐进地融入贝叶斯最佳判定面. PNN 训练时间短、不易产生局部最优，且它的分类正确率较高. 研究表明概率神经网络收敛速度快，具有很强的容错性、扩充性能好等特性.

2 GA-MI 算法研究

由于特征评价函数与遗传算法的收敛速度和最优解息息相关，所以提出以互信息作为算法的特征评价函数.而标准互信息只考虑了单个特征的影响，没有考虑两两特征和多个特征间的相互影响，因此，本文引入改进的互信息公式结合遗传算法来进行特征选择方法:将遗传算法里的特征评价函数用改进互信息公式进行替换. 遗传算法是一种基于封装式的特征选择算法，互信息是一种基于过滤式的特征选择算法，故GA-MI 算法是对封装式和过滤式这2种特征选择算法的结合.具体方法如下:

(1)将解空间映射到编码空间，每个编码对应问题的一个解.本文采用经典的二进制编码.

(2)设P 为种群的大小，L 为个体的长度;N 表示初始种群的大小，为用户自定义的参数，且1≤N≤P.分别对初始种群中的个体随机附上二进制值，以这N 组串结构作为初始点开始迭代.

(3)计算种群的适应度. 本文选取改进的互信息公式［6］作为适应度函数:

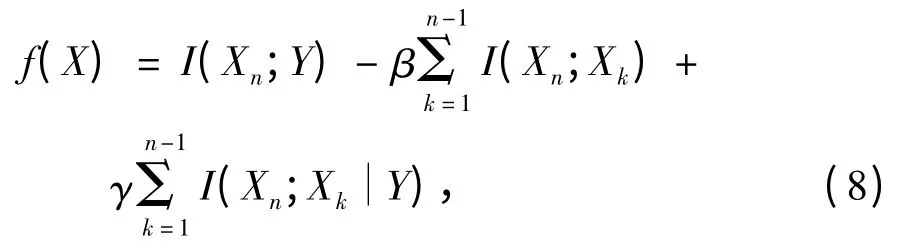
其中，n 表示特征总数，Xn表示n个特征里面任一特征值，Xk表示第k 列的特征值，Y 表示标签列，参数β 和γ 在［0，1］里面取值. 上式第1 项为所有特征与标签的互信息的和，第2 项为所有不相同的2个特征的互信息的和，第3 项为所有不相同的2个特征与标签项的互信息的和，其中第2 项、第3 项分别乘以参数β、γ，以此来削弱它们在互信息公式中的影响力.当β 和γ 均为0 时，式(8)为最原始的互信息公式.

由于式(8)为该种群所有特征的互信息，所以单个特征的互信息应除以所选特征变量的个数，即:

(4)判断是否达到迭代次数，若是，则输出当前的最优特征子集，否则执行以下步骤.

(5)执行选择操作. 本文的选择操作选用比例选择算子，即个体被选中并遗传到下一代种群中的概率与该个体的适应度大小成正比.

(6)执行交叉操作. 本实验的交叉操作采用单点交叉算子.

式中：Kj(Nx)表示待评对象Nx关于等级j的综合关联度；kj(xj)表示待评对象Nx关于等级j的单指标关联度j=(1,2,…,m)；ai表示各指标的权重。若

(7)执行变异操作. 本实验的变异操作采用单点变异算子.

(8)返回4).

3 实验方法

3.1 实验数据

本次实验数据选自UCI 机器学习数据库和人工数据集.从UCI 中选取了IRIS 数据集和Wine 数据集;设置了2 组人工数据集，选择数据集和异或数据集.其中，选择数据集(Select)为512* 10 维的数据:前9 列为特征项，其中第1、2 列的4 种排列组合的值，顺序选择第6、7、8 或9 列，所选的那一列对应的值即为第10 列标签项的值. 异或数据集(XOR)为32* 6 维的数据:前5 列为特征项，第6 列标签项的值为第1 列和第5 列异或的结果.在每次实验时，我们都会将数据集顺序打乱. 选择其中2/3 的数据为训练数据集，1/3 的数据为测试数据集.表1 为实验的数据集.

表1 实验数据集Table 1 Experimental data sets

3.2 实验方法

为了验证所提出方法的有效性，采用GA-PNN算法和GA-PNN-MI 算法与本文所提出的方法进行比较.

GA-PNN 算法是将遗传算法中的初始种群特征值随机选择改为用PNN 进行选择. 具体实现:首先用PNN 预测每个特征单独使用时的情况，并算出每个基因位的方差，然后选择方差倒数值不小于均方差倒数值的基因位，此基因位的特征即作为遗传算法初始种群的特征. 选择、交叉、变异操作同前面的GA-MI 方法，适应度函数为测试集数据误差平方和的倒数.

GA-PNN-MI 算法是在GA-PNN 算法的基础上，将GA-PNN 中的适应度函数变为改进的互信息公式.

GA-MI 算法与GA-PNN-MI 算法最大的区别在于后者用PNN 对遗传算法里的初始种群进行选择，而非随机选择选择初始种群.

4 结果与分析

对每种方法各做15 组实验.实验结果显示，遗传算法中初始种群大小N 取10，互信息公式中参数β、γ 取值分别为0.5、0.6 时，实验结果较为理想.对于表1 中的每一个数据集，分别运行GA-MI、GAPNN 和GA-PNN-MI 算法，记录下各算法得到的特征子集.统计每次实验所得特征子集的个数，取这15 组数据的平均值，即为所选择特征子集个数. 特征个数采用向上取整的方法.所选特征为15 组数据中出现次数最多的特征. 特征个数及所选特征见表2 和表3. 表2 列出了采用3 种不同特征选择方法得到的特征子集中所包含的特征的个数，表3 列出了对应的特征子集所包含的具体特征的下标.显然，采用本文提出的GA-MI 方法选出的特征子集规模小于或等于其他2 种方法.

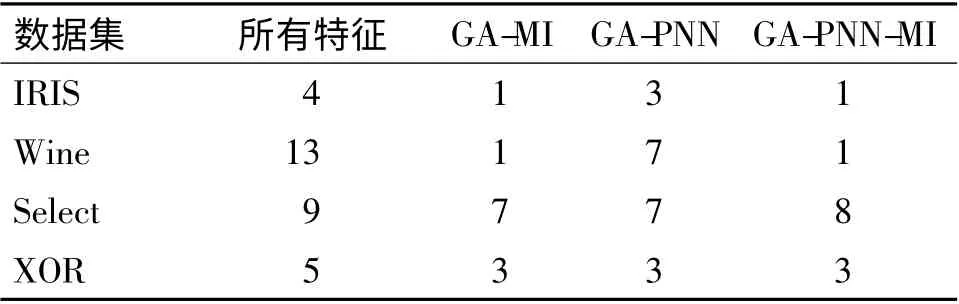
表2 3 种特征选择算法得到的特征子集大小Table 2 The feature subset size in three feature selection algorithm

为了对比PNN 和BP 网络的优劣及验证所选择特征的情况，我们将以上3 种方法选出的特征分别应用在PNN 和BP 这2 种神经网络的分类器中，其分类正确率见表4 和表5.

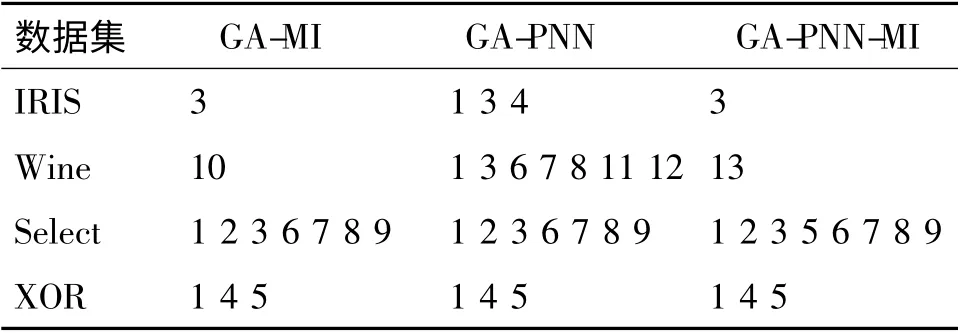
表3 3 种特征选择算法得到的特征子集Table 3 The feature subset in three feature selection algorithm

表4 PNN 分类器在各特征子集上的分类精度对比Table 4 The comparison of classification accuracy in each PNN classifiers with feature subsets %

表5 BP 分类器在各特征子集上的分类精度对比Table 5 The comparison of classification accuracy in each BP classifier with feature subset %

从表4 和表5 看出，大多数情况下，采用选择后的特征子集进行分类，分类精度都会有所提高，这充分说明了特征选择对于提高整体性能的必要性和重要性.对比表2 和表4，尽管用GA-MI 方法选择的特征个数比用GA-PNN 或GA-PNN-MI 方法选择的特征个数少，但是用于分类时分类精度并未比其他方法有显著下降，说明GA-MI 算法可以选择出更为有效的特征变量;更重要的是，对比表4 和表5，不难发现，在改用BP 网络分类器进行分类时，GA-PNN和GA-PNN-MI 这2 种方法的分类精度都有所下降，而GA-IM 算法的精度基本保持不变.其他2 种方法分类精度下降的原因是这2 种方法采用PNN 的分类精度作为特征选择的标准，因此，改用BP 网络分类时精度就发生变化，这一结果说明GA-IM 方法具有较好的泛化特性. 另一方面，从表4 还可看到，对于数据维度较低的数据集GA-MI 方法在降维和分类精度方面都比其他2 种方法要好，但是，对于数据维度较高的Wine 数据集(13 维)，GA-MI 所选的特征子集在分类时的精度低于其他2 种方法，其原因在于，采用GA-MI 方法进行特征选择时，为控制算法运行时间，并未达到最优结果就人为停止算法过程，所以选出的特征子集并非最优子集，从而导致其分类精度较差.

5 结束语

本文提出一种由遗传算法和改进的互信息公式结合的特征选择方法. 将遗传算法里的特征评价函数换为改进的互信息公式来对特征进行选择，结合了过滤式和封装式这2 种特征选择方法的优点. 实验结果表明采用GA-MI 方法不仅选出真正有效的特征显著从而降低数据的维度，而且所选出的特征具有较好的泛化能力，对于不同的分类器具有更好的适应性.但是，程序编写只考虑了方法的实现，没有考虑程序的执行效率，造成对于高维数据程序运行需要的时间较长. 在未来的工作中将进一步改进算法效率，进行高维度数据的特征选择实验，更好地验证该方法的优良性能.

［1］Liu H，Yu L. Toward integrating feature selection algorithms for classification and clustering［J］. IEEE Trans on Knowledge and Data Engineering，2005，17(3):491－502.

［2］蒋盛益，王连喜. 基于特征相关性的特征选择［J］.计算机工程与应用，2010，46(20):153－156.Jiang S Y，Wang L X. Feature selection based on feature similarity measure［J］. Computer Engineering and Application，2010，46(20):153－156.

［3］Zhang D Q，Chen S C，Zhou Z H. Constraint score:A new filter method for feature selection with pair-wise constraints［J］. Pattern Recognition，2008，41(5):1440－1451.

［4］王小平，曹立明.遗传算法理论应用与软件实现［M］.西安:西安交通大学出版社，2002.

［5］陈明.MATLAB 神经网络原理与实例精解［M］.北京:清华大学出版社，2013.

［6］Brown G. A new perspective for information theoretic feature selection［C］∥International conference on artificial intelligence and statistics.MA，USA:Microtome Publishing，2009:49－56.