基于BP神经网络的GPS/SINS 姿态测量融合算法

田增山，崔永全

(重庆邮电大学重庆市移动通信技术重点实验室，重庆400065)

0 引言

导航技术是现代科学技术中一门重要的技术，其中，姿态信息是导航的重要参数之一，广泛应用在航天、航空、航海及其他众多领域。全球定位系统(global positioning system，GPS)和捷联惯性导航系统(strapdown inertial navigation system，SINS)是应用最广泛的姿态测量技术，它们各有优缺点，采用信息融合技术把2种系统综合起来进行优化配置，使组合后的系统性能优于各子系统的性能［1］。GPS/SINS组合系统是目前最先进的全天候、自主式姿态测量技术，应用前景广泛。我国GPS/SINS组合导航起步较晚，目前已建立了配套的姿态控制系统研制和仿真试验体系，理论和技术上存在的一些问题，有关科研工作正在深入进行，力求达到世界先进水平［2］。

Kalman滤波是目前GPS/SINS组合系统采用最多的信息融合技术［3］，但它需要找出系统数学模型，对原始的非线性连续系统模型进行线性化和离散化处理，且要求系统噪声和测量噪声为零均值的高斯白噪声。对此本文提出了基于反向传播(back-propagation，BP)神经网络的GPS/SINS组合姿态测量系统，BP网络的信息融合算法不需对所求问题建模，就能够很好地逼近系统非线性特性，且计算过程稳定，能获得较高精度的姿态信息［4］。本文设计了适用于GPS/SINS组合姿态测量系统的BP网络模型，并改进BP算法，以提高网络训练速度及精度。通过MATLAB数字仿真，结果表明，改进的BP神经网络算法对于GPS/SINS组合姿态测量系统是有效和可行的。

1 BP神经网络

BP网络是目前应用最广泛的神经网络模型。BP算法属于δ算法［5］，是一种监督式的学习算法，其整个信息处理过程分为前向传播(记忆)和误差反向传播(学习)2个过程。学习目的是利用网络实际输出与目标向量之间的误差来修正权值，使网络实际输出与目标输出之间更加接近，网络输出层的误差平方和达到最小。

从结构上讲，BP网络是一种分层型网络，具有输入层、中间层(隐含层)和输出层3层结构，层与层之间多采用全连接方式，同一层单元之间不存在相互连接［6］。多层BP网络结构如图1所示。图中，第1层为输入层，只起到分配输入的作用，没有计算能力，后面的层为计算单元。输入和输出节点与外界相连，其他中间层称为隐含层。

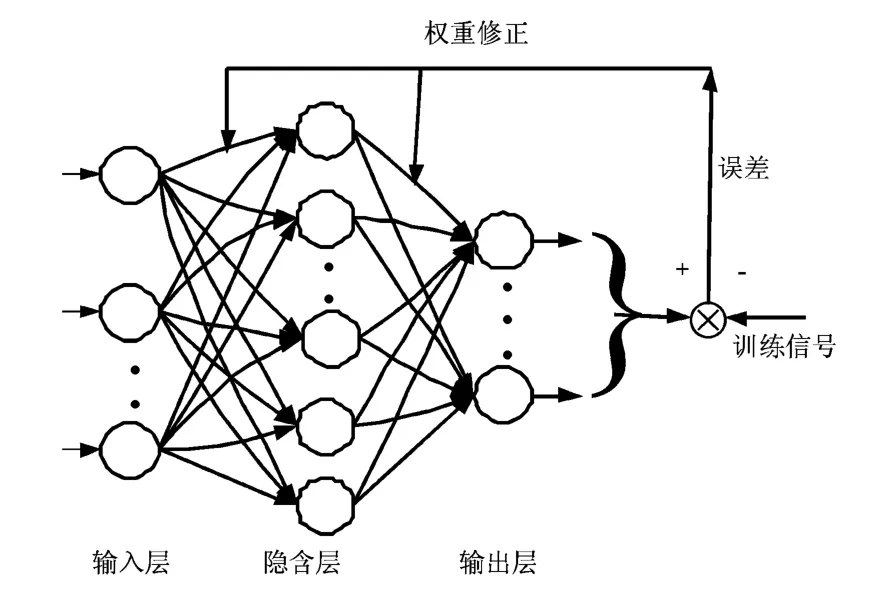
图1 BP网络结构Fig.1 Structure of BP network

标准的BP算法步骤可归纳如下［7］。

1)初始化。设输入层到隐含层的连接权值为ωij，隐含层到输出层的连接权值为ij，隐含层的阈值为θk，输出层的阈值为k，初始步长 η。

2)计算隐含层各神经元的输出

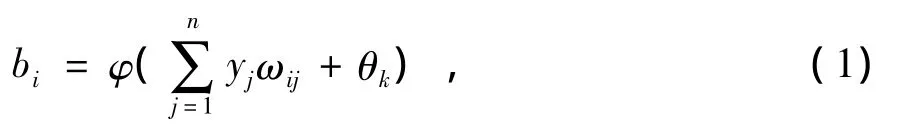
(1)式中:yj为输入层各单元输出值;φ(v)=为激励函数;i=1，2，…，p;j=1，2，…，n。

3)计算输出层各神经元的输出

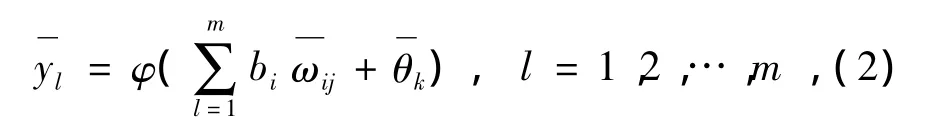
4)定义误差函数

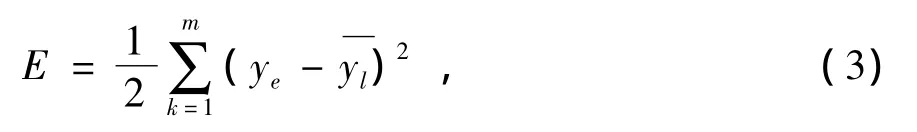
(3)式中，ye为目标的输出。

5)调整输出层的连接权值

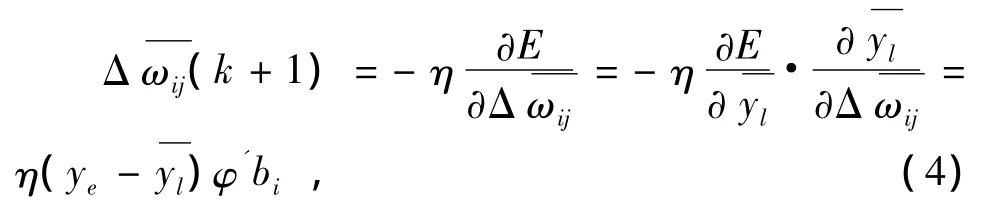
6)调整输出层的阈值

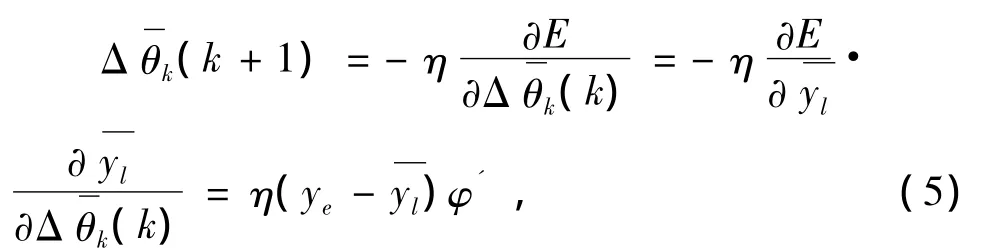
7)调整隐含层的连接权值

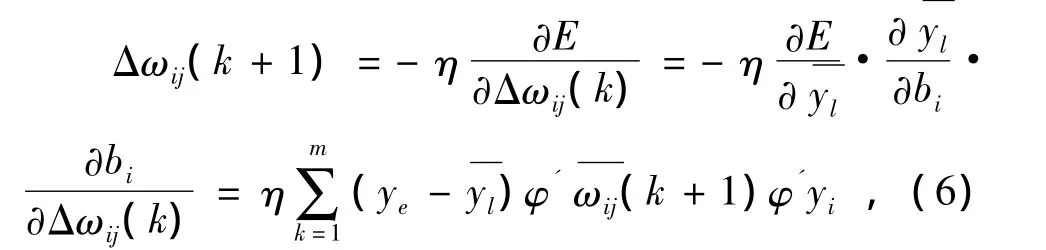
8)调整隐含层的阈值

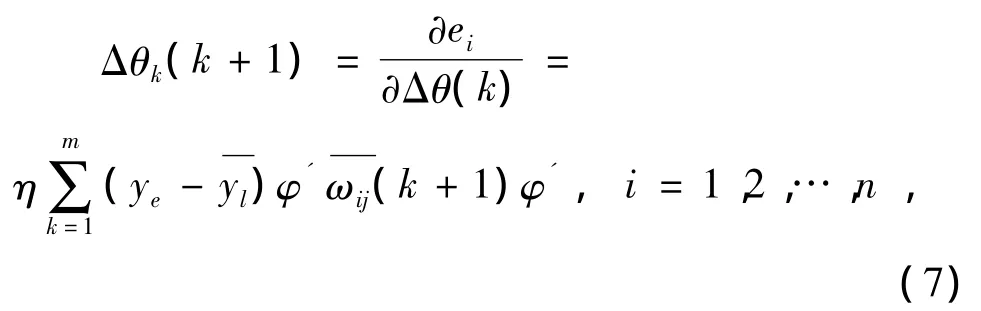
9)若误差校正值dl不满足要求，重复步骤2)→步骤8)，直至dl→0。

综上可以看出，BP神经网络学习过程是由前向计算、误差计算和误差反向传播组成。BP算法把训练样本输出与目标输出问题变为非线性优化问题，利用梯度下降法迭代求得节点之间的权值。

2 BP算法的不足及改进

虽然BP算法在实际中得到了广泛的应用，但其自身也存在一定的限制与不足，归纳如下。

1)迭代次数甚多，使得学习率较低，收敛速度慢，当处理一些比较复杂的问题时，BP算法可能要进行几小时甚至更长时间的训练。

2)网络的隐含层节点数和参数初始值的选取尚缺少统一而完整的理论指导，即没有很好的解析式来表示。

近几年已有不少人对此提出改进方案，如文献［8］提出在修改权值中加入“动量项”;文献［9］采用变步长学习率;也有文献给出了逐步增加训练数据以避免局部极小的方法和判断是否进入局部极小点的标准［10］。这些方案虽然对BP算法有一定的改进，但仍存在着不足。本文针对GPS/SINS组合姿态测量系统，进一步提出新的改进方法。

1)初始权值、阈值的设置。取［－1，1］之间的随机数作为初始权值和阈值，具有盲目性和随机性。本文先将［－1，1］的随机值分为M等分，分别随机产生初始值进行学习。选取误差函数最小的区域再N等分，再在这N个小区域内重复上述步骤。当误差函数不再减小时，认为找到了最优点，停止迭代。只要区域取得足够小，这种方法可以比较有效地避免局部行为。

2)隐含层节点的确定。隐含层神经元数一般为r≥lbn，n为训练样本数。这是一个范围值，隐含层节点少，学习过程不能收敛;隐含层节点多，节点冗余，网络性能下降。为了找到合适的隐含层节点数，应该根据环境要求，自组织地学习、调整结构，最后得到一个大小合适的模型。本文提出的解决方法:先把隐含层节点设置为一个较大的数，然后逐步合并删减，直到获得期望的误差。具体方法定义如下。

设bpi，bpj分别是隐含层节点 i，j在学习第p个样本时的输出，N为学习样本总数，则

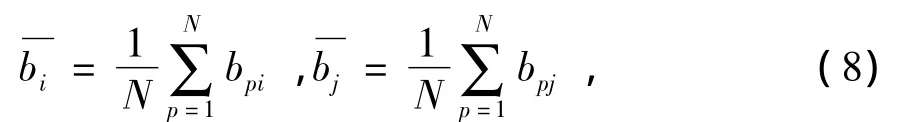
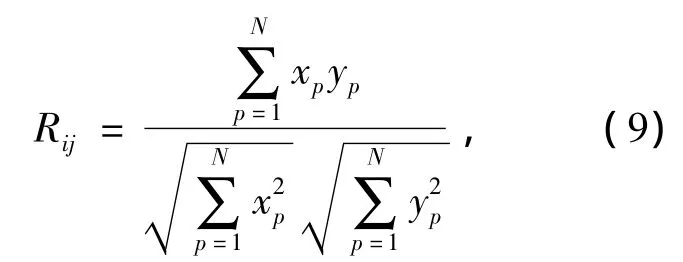
(9)式中，Rij表示隐含层节点i，j的相关程度，显然，当越接近1，表明隐含层节点i，j的线性相关程度越大，它们的功能重复，需进行压缩合并。

3)激励函数的修改。网络拓扑结构确定后，总误差函数的性质特征完全由激励函数决定。BP算法的激励函数一般选取S型函数

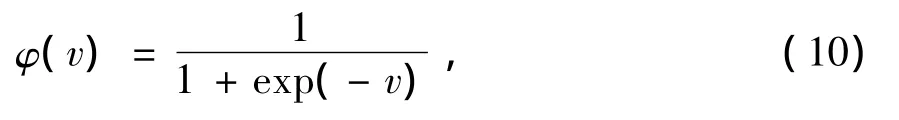
在计算中大量用到激活函数的导数，而该函数的导数为

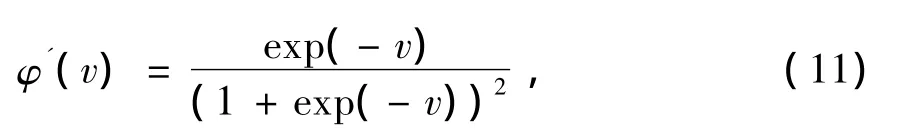
值域范围很窄，仅为［0，0.25］，使得计算出来的权重的修改量很小，从而降低学习速度。为解决这一问题，本文采用另一种双曲正切函数

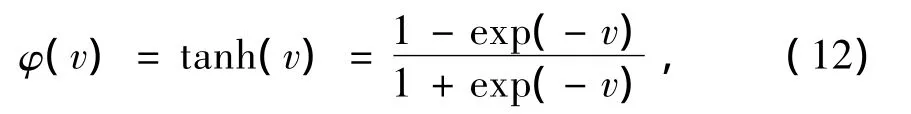
其导数为

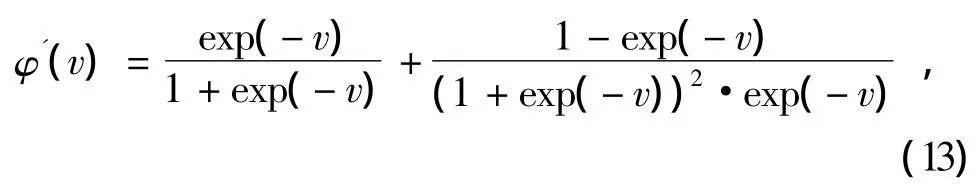
值域范围为［0，0.5］，较S型函数宽，能快速收敛。且这类函数具有平滑性和渐进性，不易陷入局部极小点。

3 仿真实验及分析

BP人工神经网络模型类似于“黑匣子”，只有输入和输出接口与外界发生联系。神经网络首先要经过网络的训练，第1节中的BP算法即为BP网络的训练过程。本文采用线性化误差小的间接法融合测量数据，将SINS与GPS的位置、速度和姿态角之差即测量值作为训练输入样本［2］，将模拟运动轨迹输出的姿态、速度和位置，以及角速度、加速度作为输出样本，对网络进行训练。

样本的输入个数对应神经网络输入层的神经元个数，期望输出个数对应神经网络输出层的神经元个数。对于训练好的BP网络模型，只要有测量信息输入网络，就能获得相应的系统状态输出。GPS/SINS姿态测量系统信息融合模型如图2所示。

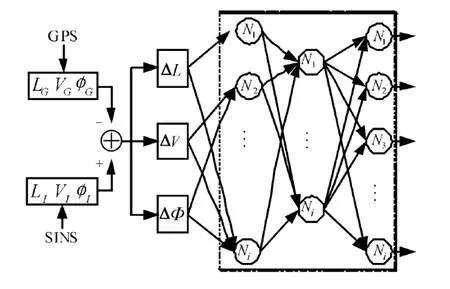
图2 GPS/SINS系统信息融合模型Fig.2 Model of GPS/SINS system information fusion

图2中，L，V，φ分别表示位置、速度、姿态角。把GPS和SINS的位置、速度、姿态角之差输入到改进后训练好的BP神经网络，就可以得到相应的系统输出。

3.1 神经网络的初始化

本文训练神经网络时所运用参数如下。

1)初始权值、阈值。根据第2节初始权值、阈值的确定方法，在选定的小区域上随机产生ωij和θk。

2)学习率η的确定。本文选用变步长学习率:先设初始步长η，若一次迭代后输出误差函数dj减少慢，则将步长乘以小于1的常数，即η=αη，α＜1，沿原来方向重新计算下一个迭代点。若下一次迭代后dj减小快，则将步长乘一个大于1的常数，即η =βη ，β＞1。η 的初始值范围为［0.01，0.8］，本文取 η =0.1;变步长学习参数 α =0.5，β =1.2。

3)网络层数及各层神经元。本文采用标准的输入层、隐含层和输出层3层模式。仿真分别采用GPS和SINS输出的位置、速度和姿态信息的差值作为测量值，即为神经网络的输入量，组合系统的姿态、速度和位置误差，以及陀螺仪漂移、加速度偏差作为神经网络的输出量。这样确定了输入层和输出层神经元数个数分别为9和l5。隐含层初始节点数设置为50，然后根据本文提出的方法，当Rij∈［0.8，1］时，就认为两节点相关性大，对其进行合并。

本文利用MATLAB神经网络工具箱提供的函数对神经网络进行训练。按照神经网络规则，输入层和隐含层神经网络的决策函数采用双曲正切函数。本文通过测试将最大训练循环数设置为5 000，训练目标误差设置为1.0×10－3。

3.2 仿真结果

根据前文的分析，按照图3所示的仿真流程对BP神经网络的GPS/SINS组合姿态测量系统进行仿真。用于训练网络的样本个数为250，经过训练确定网络的权值和阈值，把训练好的BP神经网络模型作为GPS/SINS组合姿态测量的数据融合器。图4-图6分别表示了融合后的3个姿态角误差曲线图。

BP神经网络的GPS/SINS组合方法能有效地克服SINS测姿误差状态的发散问题，同时与Kalman滤波相比，精度有明显提升且更加均匀。改进后的BP神经网络精度明显优于改进前，在运行条件相同情况下，改进前后BP神经网络方法的运行迭代次数相差较大(见图7、图8)，后者约为前者的1/3，因而后者会更快地收敛，统计表如表1所示。

图3 仿真流程图Fig.3 Simulation flowchart

图4 俯仰角误差Fig.4 Error of pitch angle

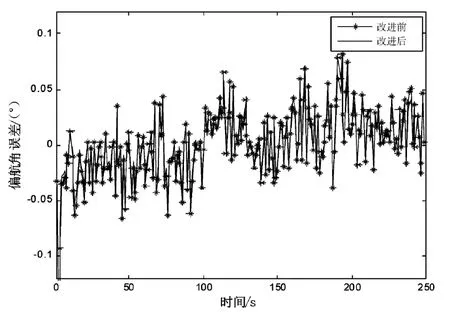
图5 偏航角误差Fig.5 Error of drift angle

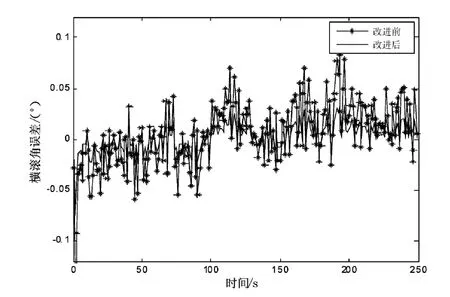
图6 横滚角误差Fig.6 Error of roll angle

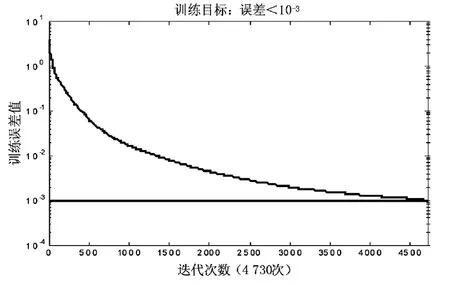
图7 BP网络改进前训练结果Fig.7 Training results before improvement

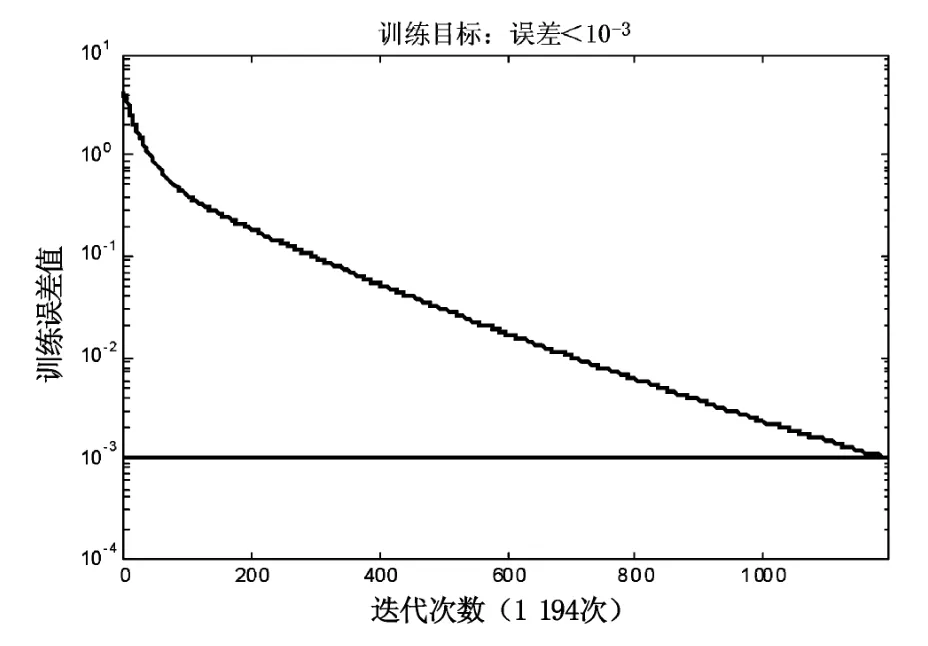
图8 BP网络改进后训练结果Fig.8 Training results after improvement

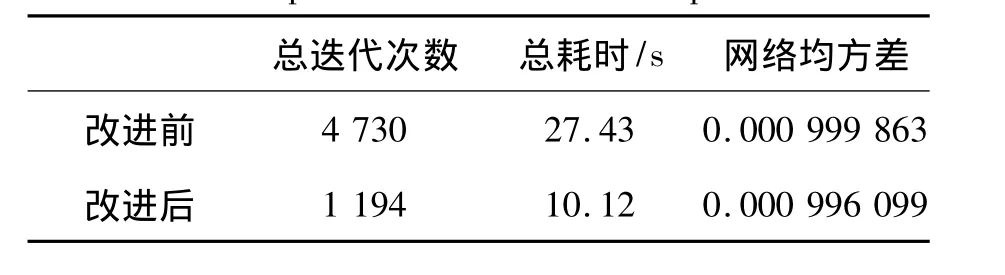
表1 BP网络改进前后对比Tab.1 Comparison before and after improvement

3.3 仿真结果分析

由MATLAB仿真得出的误差曲线图和表1可知，改进后的BP神经网络的组合系统数据融合效果显著。说明改进后的BP神经网络融合技术运用于GPS/SINS组合姿态测量系统是可行的，且与基于Kalman滤波的组合系统相比，该方法无需对所求解问题建模，能够很好地逼近系统非线性特征，获得较高精度的姿态角信息。人工神经网络计算过程稳定，不涉及矩阵求逆，其计算所耗费时间明显少于常规方法，有利于实时处理姿态测量数据。仿真结果表明，改进后的BP神经网络在GPS/SINS组合姿态测量系统中是高效可行的。

4 结束语

本文设计了适用于GPS/SINS组合姿态测量系统的BP网络模型，并在标准BP算法基础上，采用限制初始权值和阈值、动态删减隐含层节点数和修改激活函数的方法来改进BP算法，以提高网络训练速度及精度。最后利用MATLAB对GPS/SINS组合姿态测量系统进行数字仿真，仿真结果表明，基于改进后的BP神经网络组合系统姿态角误差精度明显提高，不仅克服单一SINS系统误差发散问题，而且误差精度较传统Kalman滤波融合技术得到了极大提高，改进后的BP神经网络算法在GPS/SINS组合姿态测量系统中不但高效可行，且性能优越。

［1］UHLMANN J K.General Data Fusion for Estimates with Unknown Cross Covariances［J］.Proceedings of the SPIE Aerosense Conference，1996，2755(14):536-547.

［2］方鹏.GPS/INS组合导航与定位系统研究［D］.上海:同济大学，2008.FANG Peng.GPS/INS Integrated Navigation and Positioning System［D］.Shanghai:TongJi University，2008.

［3］LIU Jinfang，DENG Zili.Information Fusion Kalman Filter for Two-Sensor System with Time-Delayed Measurements［J］.Procedia Engineering，2012，29(6):623-629.

［4］YUE Xiaokui，YUAN Jianpin.NeuralNetwork-based GPS/INS Integrated System for Spacecraft Attitude Determination［J］.Chinese Journal of Aeronautics，2006，19(3):233-238.

［5］ZHANG Tao，XU Xiaosu.A new method of seamless land navigation for GPS/INS integrated system［J］.Measurement，2012，45(4):691-701.

［6］马锐.人工神经网络原理［M］.北京:机械工业出版社，2010:9-11.MA Rui.Principles of Artificial Neural Networks［M］.Beijing:China Machine Press，2010:9-11.

［7］GAO Shesheng，ZHONG Yongmin，ZHANG Xueyuan，Bijan Shirinzadeh.Multi-sensor optimal data fusion for INS/GPS/SAR integrated navigation system［J］.Aerospace Science and Technology，2009，13(5):232 – 237.

［8］李翱翔，陈健.BP神经网络参数改进方法综述［J］.电子科技，2007，29(7):79-82.LI Aoxiang，CHEN Jian.Summarize of Parameyer Improve Methods for BP Neural Networks［J］.Electronic Sci ＆Tech，2007，29(7):79-82.

［9］贾丽会，张修如.BP算法分析与改进［J］.计算机技术与发展，2006，16(10):101-107.JIA Lihui，ZHANG Xiuru.Analysis and Improvements of BP Algorithm［J］.Computer Technology and Development，2006，16(10):101-107.

［10］张国翊，胡铮.改进BP神经网络模型及其稳定性分析［J］.中南大学学报:自然科学版，2011，42(1):115-124.ZHANG Guoyi，HU Zheng.Improved BP neural network model and its stability analysis［J］.Journal of Central South University:Science and Technology，2011，42(1):115-124.