视电导率函数理论在三维感应测井反演地层电导率的应用

白彦

（中国石油集团测井有限公司，陕西 西安710077）

0 引 言

三维感应测井是近10年来电导率测井的一个亮点，它可以实现对地层水平电导率、垂直电导率、各向异性地层测量及地层倾角和方位角信息的测量［1］。中国石油集团测井有限公司研制的三维感应测井仪器可以提供98条曲线，对应感应电动势的实部［2］。通过对98条原始数据曲线进行数据处理，可以确定地层垂直电导率和水平电导率。用三维感应测井反演地层水平和垂直电导率的研究工作已经开展多年［3－6］，主要利用多参数非线性迭代反演方法［7］。这种方法用于一维和二维层状地层的资料反演［8－9］速度一般较慢，很难满足现场实时处理要求。

视电导率函数理论是地层条件下电磁场理论研究的重大发现，其核心思想是电场格林函数中的传播系数是场点坐标的函数［10］。为了从98条原始数据曲线中提取水平电导率和垂直电导率，本文应用该理论建立了三维感应测井仪器在均匀单轴各向异性介质3种坐标系的磁场张量的解析表达式，同时建立了磁场张量的正演解析计算方法，结合阵列三维感应提供测井资料，提出了一种数据视值转换方法。首先选择短源距高频9个分量子阵列提取仪器倾角、自旋角、水平电导率和垂直电导率；其次，固定仪器自旋角，分别由其他频率阵列提取各自水平电导率和垂直电导率，仪器倾角值只作为参考；最后，已知仪器倾角，采用阻尼型高斯－牛顿反演方法［11］将测量矩阵标准化，设定地层类型提取反演初值，通过反演误差判定地层类型和反演参数值，即参数视值。

1 三维感应线圈系结构

三维感应测井仪器是由3个轴向的发射线圈（Tx，Ty，Tz）与3个轴向的接收（Rx，Ry，Rz）线圈和3个轴向的屏蔽线圈（Bx，By，Bz）组成的三线圈系结构，能够同时测量出9个分量（XX，XY，XZ，YX，YY，YZ，ZX，ZY，ZZ）（见图1）。三维感应三线圈系结构由发射线圈（Tx，Ty，Tz）、屏蔽线圈（Bx，By，Bz）与接收线圈（Rx，Ry，Rz）各3个且按三坐标系正交同心构成。屏蔽线圈主要是抵消发射线圈直接耦合在接收线圈的一次场信息，以让接收线圈获取经过地层的二次场信息。图1中，接收线圈与屏蔽线圈感应的涡流方向是反向，与发射线圈是同向。

图1 三维感应测井三线圈系发射接收线圈示意图

通过该结构的三维感应测量仪器，沿井轴移动，可以实现同时测量9个分量的地层电导率σa。式中为发射线圈在i方向上发射时，接收线圈在j方向上接收的地层视电导率信息。

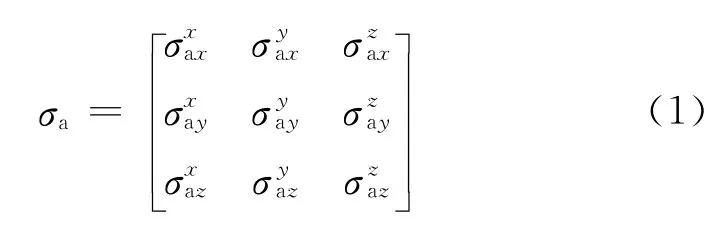
2 三维感应测井资料视值转化方法

三维感应测井资料视值转换，是针对不考虑井眼和侵入条件下的均匀介质模型，利用三维感应测井9个分量提取水平电导率、垂直电导率、仪器方向角等参数。因为实际测井受到邻层和井眼等影响，这些复杂测量环境不是简单均匀介质，所以这样提取的地层参数值只是等效值，称之为视值。

2．1 建立磁场张量解析表达式

按照电场格林函数中的传播系数是场点坐标的函数的理论，建立三维感应测井仪器在均匀单轴各向异性介质3种坐标系的磁场张量的解析表达式，具体推导出三维感应测井仪器在均匀单轴各向异性介质3种坐标系的磁场张量的解析表达式。

式中，L为收发线圈之间几何距离；S为收发线圈之间和各向异性相关的等效距离；θ为仪器对各向异性轴倾角；γ为仪器自转方位角；kv、kh分别为对应垂直和水平电磁参数，其中，kv＝kv（x）＝x为场点的位置矢量；这里的电导率、介电系数都是场点坐标的函数［10］。

利用磁感应张量波分解方法将式（2）改写成

考虑到三维感应测井工作频率较低，但精度要求不高时可以略去电磁波传播效应（趋肤效应），公式进一步简化，易于提取仪器参数和地层电磁参数。所谓低频近似，指khL→0，kvS→0，即（khL）n→0，（kvS）n→0，n≥1，代入式（3）可得到对应简化表达式

通过求解式（4），可同时求得θ、γ、σh、σv这4个参数，不必进行响应矩阵的坐标变换。

2．2 三维感应视值快速迭代反演

根据测井响应资料（x）＝（x1，x2，…，xN），i＝1，2，…，M（M为测井采集数据点数），定义目标函数O（x）。这里x＝x（σh，σv，θ，γ）为待反演参数，（x）为x的非线性函数［5］。mi（x）为正演计算测井响应值。

设一个参数空间初始猜想位置矢量xk，得到

式（11）写成矢量形式

式中，p＝［x－xk］，J＝∇（xk）。

将式（12）代入式（11），则目标函数为

式中，W和I为对角矩阵；W为权因子矩阵；I为正则化因子矩阵，可以起到保持稳定收敛的作用。这样通过式（13）线性化，目标函数写成关于p二次型的函数，满足目标函数最小值的最优解应满足

将式（14）代入（式13）可得高斯－牛顿法反演方程

通过求解式（15）可完成一次反演迭代，重复这种迭代过程，直到误差矩阵变为零或极小值时，所得到的x就是反演结果。

为此，三维感应测井资料视值转化处理问题归结为正反演问题。正演问题是已知地层电参数的分布和仪器参数求出测井响应，正演计算应用视电导率函数理论，建立了三维感应测井仪器在均匀单轴各向异性介质3种坐标系的磁场张量的解析表达式。反演问题是已知测井响应反推出地层的电参数分布，进而为判定地层属性提供物理依据。本文主要采用阻尼型高斯－牛顿反演地层参数，首先，将测量矩阵标准化，实际上就是将测量等效电导率转化为对应磁场张（分）量矩阵；其次，设定地层类型提取反演初值，这一步仪器自旋角可以高精度提取，其他参量只能获得近似值；再次，开始反演；最后，通过反演误差进行判定，判定地层类型和反演参数值，即参数视值。

3 应用实例与分析

为检验上述方法的正确性，处理了某井204～305m层位的测井数据。图2为不考虑井眼和侵入时均匀各向异性介质中水平地层电导率、垂直地层电导率反演实例。第1道为ZZ分量测量的原始信号，第2至第5道分别为4个阵列线圈测量的XX、YY主分量对应的原始曲线，第7、第8道分别是三维感应测井资料视值处理得到的地层水平电导率和地层垂直电导率，第9、第10道分别是ZZ分量2ft＊非法定计量单位，1ft＝12in＝0．3048m，下同合成处理曲线和视值处理的地层水平电导率和地层垂直电导率与90in曲线对比结果，第11道分别是各向异性、仪器轴倾角和方位角。从原始数据曲线来看，测井数据对层位响应明显，可以很好地识别地层层位。可以看出，第10道上220～240m和282～290m层位，地层垂直电导率与水平电导率数值和曲线形态一致；地层水平电导率接近垂直电导率，和ZZ分量数据合成2ft和90in电导率曲线数值相当，第11道对应的各向异性系数接近1，与理论认识相吻合。在整个层段的薄层上，可以看出地层水平电导率不等于垂直电导率，且地层垂直电导率对层位反映敏感，对每一个小的薄层都能进行很好的显示。这表明，处理结果具有很好的识别地层层位作用，验证了应用该方法反演均匀各向异性介质水平地层电导率和垂直地层电导率的正确性。

图2 三维感应视值转化测井资料处理成果图

4 结 论

（1）应用视电导率函数理论，建立了三维感应测井仪器在均匀单轴各向异性介质中3种坐标系的磁场张量解析表达式。该表达式可以直接计算，能够满足实时处理要求，大大缩短了反演的计算时间。

（2）利用参数视值转化方法对实际测井数据进行处理计算，实现了地层水平电导率和地层垂直电导率的快速反演。

（3）这种视值转化方法对实际数据进行处理应用表明，该方法具有较好的准确性和识别精度，为进一步理解三维感应测井响应特征和组合测量提供了理论依据。

［1］Zhdanov M，Kennedy D，Peksen E．Foundations of Tensor Induction Well－logging［J］．Petrophysics，2001，42（2）：588－610．

［2］张庚骥．电法测井［M］．北京：石油工业出版社，1986．

［3］Davydycheva，et al．Formation Dip and Azimuth Determination and Resistivity Determination Using Multiaxial Induction Measurements：US Patent，0082255［P］．2010．

［4］Weiss C J，Newman G A．Electromagnetic Induction in a Fully 3－D Anisotropic Earth［J］．Geophysics，2002，67（4）：1104－1114．

［5］Abubakar A，Habashy T M，Druskin V，et al．A 3D Parametric Inversion Algorithm for Tri－axial Induction Data［J］．Geophysics，2006，71（2）：1－9．

［6］Anderson B I，Barber T D，Habashy T M．The Interpretation and Inversion of Fully Tri－axial Induction Data：A Sensitivity Study［C］∥ The SPWLA 43rd Annual Logging Symposium，2002．

［7］Rosthal R，Barber T，Bonner S．Field Test Results of an Experimental Fully Tri－axial Induction Tool［C］∥The SPWLA 44th Annual Logging Symposium，2003．

［8］Hanming Wang，Sofia Davy，Sofia Davydycheva，et al．Sensitivity Study and Inversion of the Fully Triaxial Induction Logging in Cross－bedded Anisotropic Formation［C］∥SEG Annual Meeting，Las Vegas，2008．

［9］Yu L，Kriegshauser B，Fanini O，et al．A Fast Inversion Method for Multi－component Induction Log Data［C］∥SEG 71st Annual International Meeting，2001．

［10］李剑浩．感应测井视电导率和真电导率关系的积分方程［J］．中国科学：地球科学，2014，44（5）：928－933．

［11］邢光龙，杨善德，李曙光．电磁波测井资料反演中Jacobi矩阵的快速算法及其特性分析［J］．地球物理学报，2007，50（2）：642－650．