基于反距离夹角加权算法的地理信息空间内插方法

何立恒，鲍其胜，王 庆

(1.南京大学地理与海洋科学学院，江苏南京210046;2.南京林业大学土木工程学院，江苏南京210037;3.南京市测绘勘察研究院有限公司，江苏南京210019)

一、引 言

在地理空间信息领域，为了获得空间信息，需要实测空间数据，而实测的空间数据往往是离散点的形式，或者是分区数据的形式［1］，这些实测的空间数据集被称为已知的空间样本，实测的点则被称为已知样本点。即使实测空间数据达到相当的密度，也不足以表示复杂的地理空间形态，亦即常规方法无法对地理空间中所有点进行观测，因此需要通过空间内插来增补表达地理空间的空间数据。

空间数据内插是用实测的空间数据来估算(预测)未知空间数值的过程［2］。根据已知的离散点数据或已知的分区数据来估计(推算)任意点或区域数据的方法称为空间内插，前者称为点内插，后者称为面内插［3］。通过内插可以生成或补充已知数据的不足，广泛应用于等值线制作、高程模型建立、数据格网化和地理区域空间分析与比较研究等。

1970年，美国地理学家W.R.Tobler提出地理学第一定律，指出“任何事物都是与其他事物相关的，但是距离近的事物比距离远的事物相关性强”，这也是一切空间内插方法的依据［4］。空间内插方法众多，各方法又有其本身的诸多前提、参数、适用范围等，但从本质上说，内插均遵循的是临近点之间具有相似性这一原则［5］。就目前的研究而言，大多数的内插是根据周围的已知数据，从这些已知数据推求一个函数关系式，使该关系式最好地逼近这些已知的空间数据，并能根据该函数关系式推求出区域范围内其他任意点或任意分区的值［6］。通常被熟知和利用得较多的就是点内插。

二、反距离加权法及存在的问题

1.反距离加权平均算法介绍

在空间点内插时，反距离加权插值(inverse distance weighting，IDW)具有计算相对简单、操作便利等特点，是常用的几何内插方法之一。该方法认为与内插点距离最近的若干个已知样本点对内插点值的贡献最大，其贡献大小与距离成反比［1-8］。其数学理论是加权平均，即将已知样本点各数值乘以相应的单位数(权数)，然后加总求和得到总体值，再除以单位数之和。假设xi为已知样本点，wi为已知样本点对应的权数，y为加权算术平均数(即预测值或内插值)，则加权算术平均数的计算公式为

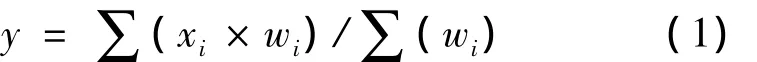
反距离加权法中的权数wi由式(2)来确定，为

式中，PDi为内插点与已知样本点之间的距离;u为距离PDi的幂。

由式(1)和式(2)可得反距离加权平均数的计算公式为

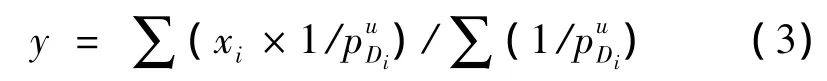
反距离加权法中，需要考虑距离的幂和邻域搜索范围两个影响因素［7］。Husar等［9］的研究结果表明，幂越高，内插结果越具有平滑的效果。u即为控制参数，u值越大，权重随距离增大衰减得越快;反之，u越小，权重随距离增大衰减得越慢，一般u取1～3［3］。同时，在给定邻域搜索范围后，可利用的已知样本点就具有确定性。从内插方法的误差公式可明显得出，已知数据的间距大小是影响内插精度的最重要因素，间距越小，精度越高［10］。

2.反距离加权平均算法存在的问题

假定在内插点所用的已知样本点中，其中只有一个点距离内插点很近，其他很多已知样本点距离内插点较远，但这些较远的已知样本点差不多都在同一位置(也可认为是重复点)。这种情形运用反距离加权法将导致计算的内插值不接近距离近点值。因此，探索新的加权因子，提高地理信息空间模拟的逼真性和合理性是非常必要的。

如图1所示，假定已知样本点A与内插点P的距离为1个单位，点值为2.00，另10个已知样本点B1、B2、…、B10与内插点 P 的距离为10个单位，点值均为20.00。B系列点是彼此很近的点或者就是重复点，为了更好地反映重复点的影响，这里取幂值u为1(以下计算均取幂值u为1)，依反距离加权算法，利用式(3)计算P点的内插点值为=11.00，此值相对靠近较远的B系列点的值，不接近距离近点A的值。

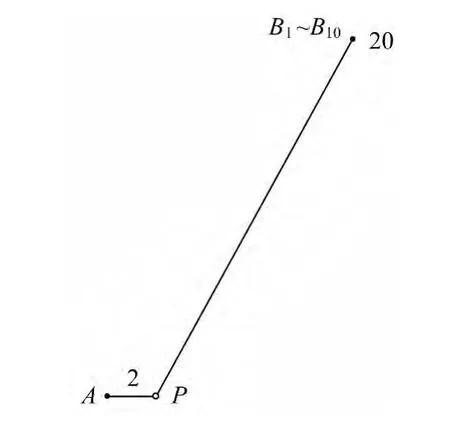
图1 内插点位图1

实际上，由于点值为20.00的点基本在空间同一位置，相当于重复点或者就是重复点，在实际内插作业中所发挥的作用应类同于一个点，则此时内插点P的值应为3.64，此内插值接近较近点A点值。

探索既考虑已知样本点与内插点之间的距离，又考虑已知样本点在内插点周边的方位分布和密度的加权因子，将解决上述问题。

三、反距离夹角加权算法

在土方工程量计算的野外数据采集时，地形规则的地区，采点相对稀疏，而地形变化复杂的地区，点位采集相对密集。除了距离这个因素影响内插点外，再引入夹角作为定权要素，提出反距离夹角加权算法，可以解决已知样本点在内插点全圆方位上分布不均及已知样本点疏密不匀对内插值的影响。

距离定权方式不变，夹角则选择以内插点为顶点，内插点与所有已知样本点所构成的最小角为其权值。图1 中，以P 点为顶点，P 点与B1、B2、…、B10这10 个点中任意两点所构成的夹角显然比P点与B1、B2、…、B10中任意一点和A点所构成的夹角要小得多。引入距离和夹角作为定权因子，样本点的权值计算公式为

式中，pαi为夹角权因子，取内插点与已知样本点和其余已知样本点中的最小夹角;pDi为距离权因子，取内插点到已知样本点的距离。

由式(1)和式(4)得反距离夹角加权平均数计算公式为

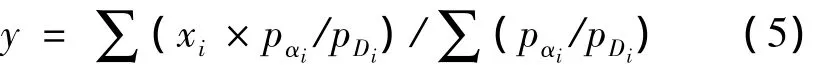
假定的距离值及样本点的点值不变，设P点与A点和B1～B10点所构成夹角的最小角为120°，P点与B1、B2、…、B10中任意二点构成的最小夹角为0.5°，代入式(5)，可得利用反距离夹角加权法计算内插点的点值约为2.07。

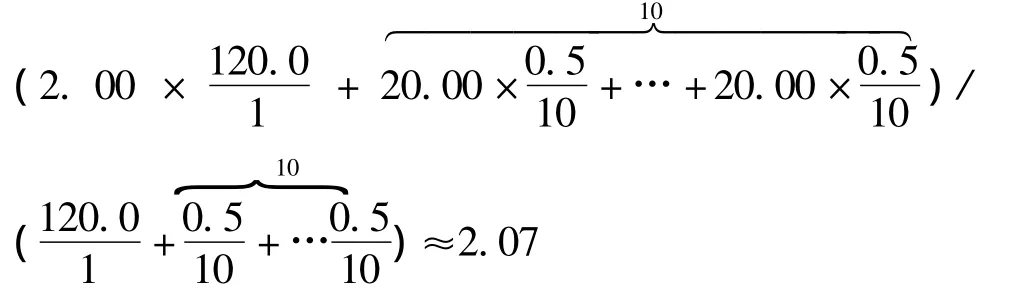
此值更接近较近点A的值，减弱甚至消除已知样本点密度不均和在内插点全圆方位分布不匀对内插值的影响。

四、内插过程及实例比较分析

1.内插过程

反距离夹角加权算法进行几何内插的步骤如下:

1)设计内插规则，确定内插点的位置。在数据内插处理中，一般是先设计内插规则，内插规则确定了内插点的位置。DEM构建、数据的格网化、图像变换处理等都是先设计内插规则。图2即为规则格网DEM矢量数据内插图，离散点为已知样本点，方格顶点的值需内插得出。

图2 规则DEM内插格网点及已知样本点值图

2)根据内插点的数据特征，选定与内插点具有相同数据特征的可利用已知样本点，图2中所有离散点即为可利用已知样本点。

3)在已知样本点中选取某一内插点的可用点集S，已知样本点的选取可以根据距离和数量等因素来确定，选取的原则有两个方面:一是已知样本点的位置相对内插点应尽可能均匀分布;二是所选取的参与计算内插值的已知样本点数目应该适当。一般是以内插点为圆心，给定搜索半径，在搜索半径内找已知样本中的该内插点的可用点集S，总数为N;若不够点数，便加大搜索半径，直至搜索半径上限或显示已知样本点不够。若是规则内插，搜索半径一般为规则内插点间距的1～2倍，N≥3。

4)在S中选取任意已知样本点Ni，计算此内插点与已知样本点Ni之间的距离Di，计算此内插点与Ni和S中其余已知样本N-1个点的夹角，在N-1个夹角值中筛选出最小值得αi。若出现样本点重合或在同一方向线上，此夹角值为零。为了充分利用所有的样本点，避免夹角权值为零而影响Wi，可以将αi给定一微小值，如10-6。

5)重复步骤4)，分别求此内插点与点集S中其余N-1个已知样本点间的距离D和最小夹角α。

6)利用式(5)计算内插点的内插值。

7)重复步骤3)—步骤6)，直至所有内插点的内插值计算结束。

2.实例比较及分析

用不同的内插方法对图1和图3—图7进行内插值计算。假设图中都只有一个点值为2.00的已知样本点A，并与内插点的距离都为1;其他已知样本点B1—B10的值均为20.00，并与内插点的距离为10或5;样本点值的单位可以为米或其他，各方法计算出的内插值的单位与样本点值的单位相同;距离和角度的单位可以是任意长度单位和角度单位。计算结果见表1。

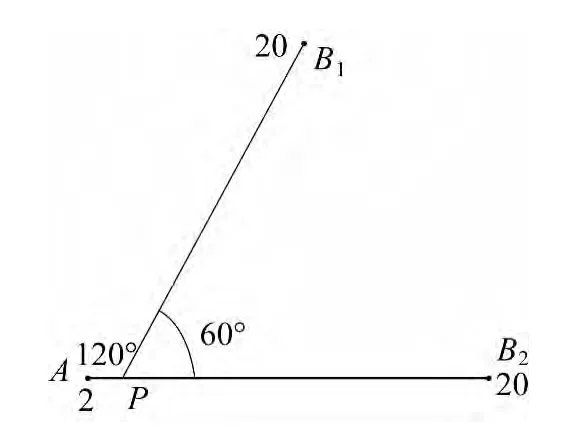
图3 内插点位图3

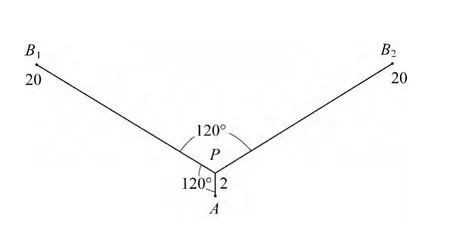
图4 内插点位图4

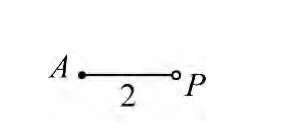
图5 内插点位图5

图6 内插点位图6

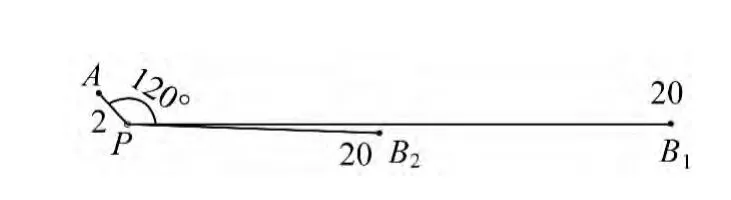
图7 内插点位图7

在内插理论中，当内插点正好位于已知样本点位置时，可认为内插特征值就是该已知样本点值，亦即此点不需要内插。设计实例用反距离夹角加权法进行内插时，充分考虑到内插点P接近已知样本点A，这样，可假定内插真值接近A点值。从表1可以看出，相对于算术平均值法和反距离加权法，反距离夹角加权法内插结果波动范围小，也更接近假定内插真值，而邻近点值法的值只跟最近点值有关，无论其他样本点怎样变化。当已知样本点少于3个或在全圆方位上分布均匀时，反距离夹角加权法和反距离加权法推求的值是相等的。

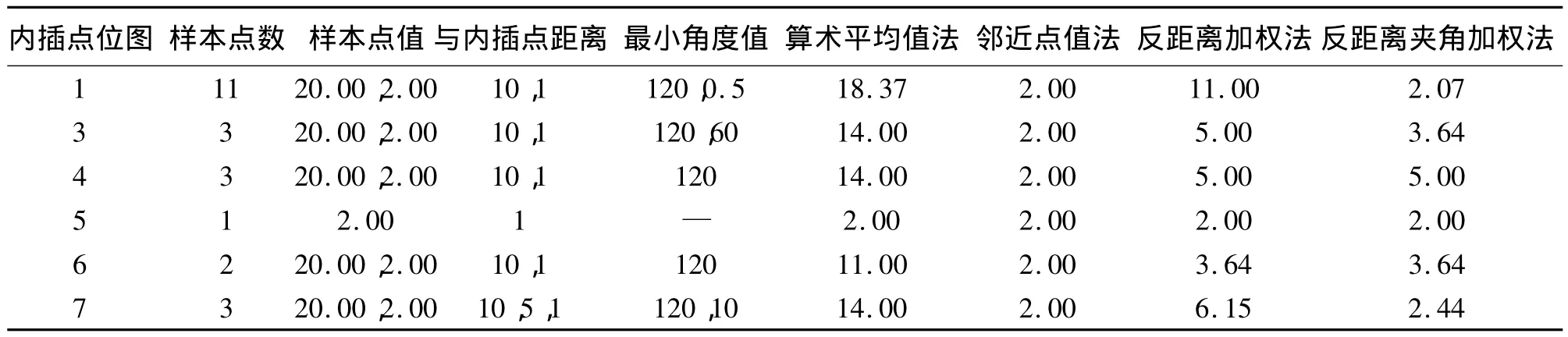
表1 不同内插算法计算结果表

五、结束语

空间内插是用已知样本点的数据来估算内插点的数值过程，把离散数据转换成规则数据或增加内插数据。从反距离夹角加权算法应用在地理信息空间数据内插中可以看出，当已知样本点只有一个时，该算法相当于最邻近值法;当只有两个已知样本点，或者多于两个已知样本点并且点位在全圆方位上分布均匀时，夹角权相等，该算法相当于反距离加权法;多于两个已知样本点，但已知样本点密度和方位分布不均，反距离夹角加权法能减弱甚至消除其影响，保证内插值接近近点值。可以说，反距离夹角加权法是邻近值法和反距离加权法的改进和提伸，提出的距离加夹角的定权方法能有效减弱甚至消除在内插过程中所选定的已知样本点在内插点全圆方位上分布不均及已知样本点疏密不匀对内插值的影响。基于加权平均理论，提出的反距离夹角加权算法将广泛应用在建立DEM及图像处理等地理空间信息数据内插中。

［1］李新，程国栋，卢玲.空间内插方法比较［J］.地球科学进展，2000，15(3):260-265.

［2］CHANG K T著，地理信息系统导论［M］.陈健飞，等译.北京:科学出版社，2003.

［3］汪学兵，柳玲，吴中福.空间内插方法在GIS中的应用［J］.重庆建筑大学学报，2004，26(1):35-39.

［4］汤国安，刘学军，闾国年.数字高程模型及地学分析的原理与方法［M］.北京:科学出版社，2005.

［5］李胤，杨武年，杨容浩，等.基于移动曲面拟合算法和加权平均算法的DEM内插算法改进［J］.测绘，2010，33(4):168-171.

［6］朱求安，张万昌，余钧辉.基于GIS的空间插值方法研究［J］.江西师范大学学报:自然科学版，2004，28(2):183-188.

［7］秦涛，付宗堂.ArcGIS中几种空间内插方法的比较［J］.物探化探计算技术，2007，29(1):72-75.

［8］张靖.GIS空间内插方法与应用研究［D］.呼和浩特:内蒙古师范大学，2008.

［9］HUSAR R B，FALKE SR.Uncertainty in the Spatial Interpolation of PM10 Monitoring Data in Southern California［EB/OL］.［2012-09-17］.http:∥capita.Wustl.edu/CAPITA/CapitaReports/CaInterp/CaINTERP.html.

［10］胡海，游涟，胡鹏，等.数字高程模型内插方法的分析和选择［J］.武汉大学学报:信息科学版，2011，36(1):82-85.