基于规则格网DEM提取坡度坡向的统一模型研究

梁星 贾敦新

(重庆市地理信息中心,重庆 401121)

基于规则格网DEM提取坡度坡向的统一模型研究

梁星 贾敦新

(重庆市地理信息中心,重庆 401121)

本文通过对现有基于DEM的坡度坡向差分算法的分析,提出了基于规则格网DEM提取坡度坡向的统一计算公式,编程实现了算法的统一模型,并成功集成到了ArcGIS产品中,基于本模型可以自定义坡度坡向的计算方法,也可以通过修改参数的方法定制任意一种差分算法获取地面坡度和坡向,为科研工作者和实际应用者提供了全面有效的计算方法。

数字高程模型 坡度 坡向 统一模型

坡度坡向是相互联系的两个参数，坡度反应斜坡的倾斜程度，坡向反应斜坡所面对的方向。作为描述地形特征信息的重要指标，是水文模型、滑坡监测与分析、地表物质运动、土壤侵蚀、土地利用规划等地学分析模型的重要参数。坡度和坡向与其他参数一起使用，有助于诸如森林蕴藏量估算、水土保持、野生动植物保护、选址分析、土地利用以及其他应用问题的解决。例如，在农业土地开发中，大于25°的坡度一般被认为是不适宜耕种的，而在热带经济作物耕种规划中，坡向则是评估寒冷冻害风险的重要因子。在实际应用中，某些应用软件，例如ArcGIS等虽然提供了坡度坡向的计算方法，但是由于不同的用户在不同的地区针对不同的数据需要采用不同的计算方法，而这些应用软件就像一个黑箱，只是提供了单一的计算方法，对于用户而言很难进行选择和扩展，尤其是科研工作者，在研究不同计算方法对计算结果或者，不同数据误差对计算结果，或者不同误差在不同计算方法下的传播规律时显得束手无策。如果重新一一编程实现则显得太过麻烦也不切实际，毕竟用户和科研工作者关注的不是编程，因此本文针对以上问题，深入分析了基于规则格网DEM的坡度坡向的差分算法，提炼出了不同差分算法的统一模型，并编程实现了该模型，集成到了常用的应用软件中，极大的方便了广大科研工作者和实际应用者。

1 坡度坡向的定义

空间曲面的坡度(slope)和坡向(aspect)是互相联系的两个参数，均是点位函数，除非曲面是一平面，否则曲面上不同位置的坡度和坡向是不相等的。坡度反映曲面的倾斜程度，定义为曲面上一点P的法线方向与垂直方向(即天顶)Z之间的夹角，而坡向是斜坡面对的方向，定义为P的法线正方向在平面的投影与正北方向的夹角，如图1所示。

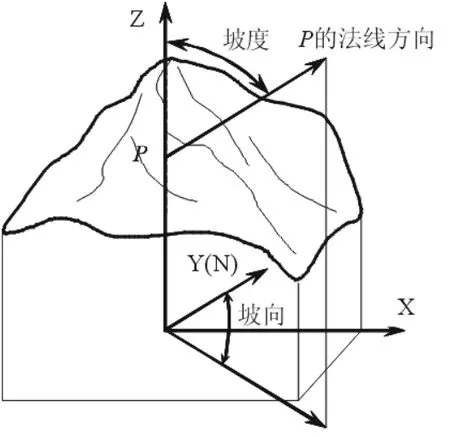
图1 坡度和坡向定义

图2 差分法坡度坡向计算原理

由数学分析知，任一空间曲面 z= f（x, y ）在平面上表示一等值线簇 f（x,y）= c(c为任意常数)， 当z为高程时则为等高线。对任意点P （x ,y ），沿P的梯度反方向，f（x, y）取得其下降最快值。在数字地形分析中，该值即为P的坡度，其下降方向即为坡向或流向。对于函数f（x,y ），P点的梯度表示为：

式中i， j为单位方向，其模(norm)即为坡度(或梯度)，表示为单位长度上的高程升降，通常以百分数表示：

表1 格网DEM坡度坡向计算数学模型

表2 三阶反距离平方权差分fx和fy对应权重

图3 坡度坡向统一模型设计

当需要计算斜坡角度时(即P的法线与天顶Z之间的夹角)，由上式我们有：

当 fy≠0时，梯度方向即为坡向，定义为：

实际工作中，坡向一般以北方向为起始方向，并按顺时针方向度量，则坡向在x轴为东西方向、y轴为南北方向(北方向)的坐标系中表示为：

2 基于规则格网DEM提取坡度坡向的统一模型

由上述表达式可知，求解地面某点的坡度和坡向，关键是求解fx和fy。DEM是以离散形式表示的地形曲面，而且在多数情况下曲面函数是未知的，因此在DEM上对fx和fy的求解，一般要进行曲面拟合或通过数值微分的方式进行。这里需要注意的是坡度坡向是地形表面的固有属性，其数学定义是严格的，并不随DEM结构的改变而改变。但由于数字高程模型仅仅是对地形曲面的一种近似，不同的模型结构可能导致不同的坡度坡向计算结果，并且计算方法也随之而异。鉴于这种考虑，我们将以使用最为广泛的规则格网DEM进行分析。

在格网DEM上对fx和fy求解，一般是在局部范围(3×3移动窗口)内，通过给格网点一定编号(中心格网点一般为5)，利用差分原理进行计算。如图2，设中心格网点为 （i, j ），相应坐标为 （xi, yj），局部地形曲面设为 z= f（x, y ），g为格网间距，则在（i, j）处的泰勒级数展开式为(取至一次项)：

式中k为展开范围，按不同的k的取值和定权方式，将产生不同的坡度坡向数学模型。表1概括了基于格网DEM的坡度坡向算法和导数计算公式。

3 基于DEM提取坡度坡向统一模型的实现

通过以上所述和表1中的总结，求解地面某点的坡度和坡向，关键是求解fx和fy。以图2为例，若求z5点的坡度或者坡向，则关键问题是求解z5点的fx和fy，而求解z5点的fx和fy的关键问题是对1-9的赋权问题，以三阶反距离平方权差分为例，fx和fy，分对应的权重如表2，因此对fx和fy的求解问题转化为对待求点周围9个点的赋权问题，对于其他的差分方法具有相同的规律，因此本文坡度坡向的统一模型设计如图3，通过选择不同的差分算法或者输入不同的权重就可以定制不同的差分算法，进而得到不同算法下的坡度坡向计算结果。本文基于C#和ArcGIS Engine开发实现了本算法，并成功的集成到了ArcGIS桌面产品中，从而更加方便的使用本算法。

4 结语

坡度坡向作为描述地形特征信息的两个重要指标受误差的影响很大，尤其是不同的误差，对于地形数据而言，区分为数据误差和模型误差，不同的算法对不同的误差敏感性不一，这与地形的复杂程度有着很大的关系，因此根据不同的数据，在不同的地区选择不同的计算方法尤为重要，因此本文将各种差分算法进行了分析，提出了统一的计算模型，并实现了算法，集成到了应用最为广泛的ArcGIS产品中，对于基于规则格网的DEM的地形分析具有重要的意义。

[1]贾敦新,汤国安,王春.DEM数据误差与地形描述误差对坡度精度的影响[J].地球信息科学,2009.

[2]刘学军.基于规则格网数字高程模型解译算法误差分析与评价[D].武汉大学博士论文,2002.

[3]周启鸣,刘学军.数字地形分析[M].北京:科学出版社,2006:282-283.

[4]王春,汤国安,张婷 等．在降雨侵蚀中黄土地面坡度变化的高分辨率研究[J].山地学报,2005(5):589-595.

梁星(1982-),男,重庆涪陵人,硕士,现为重庆市地理信息中心工程师,研究方向:地图学与地理信息系统、遥感。