随机波浪载荷下基于断裂力学的结构疲劳分析算法研究

尹彦坤，陈 实，李挺前

(湛江南海西部石油勘察设计有限公司，广东 湛江 524057)

随机波浪载荷下基于断裂力学的结构疲劳分析算法研究

尹彦坤，陈 实，李挺前

(湛江南海西部石油勘察设计有限公司，广东 湛江 524057)

应用断裂力学方法进行结构疲劳评估，Paris法则给出了简洁的计算公式，但是对于海洋结构物来说，在随机波浪载荷下的响应是非常复杂的。因此，对于结构疲劳寿命的评估，寻求一种兼顾计算效率、准确度和安全性的计算方法是非常重要的。结构的响应应力是一个随机变量，为了提高计算效率，研究了其等效恒值应力；为了保证计算结果的安全性，探讨了长期波浪分布下应力的加载次序。

随机波浪；断裂力学；疲劳；算法

0 引 言

通常认为海浪短期统计特性是平稳随机过程，波面高度的分布符合正态分布，波高的分布遵从瑞利分布，并且常用随机功率谱即海浪谱形式来描述随机波浪。波浪的长期分布通常以长期分布统计概率表的形式给出。波浪的短期分布加长期分布形成了结构的整个疲劳海况。

根据结构随机振动理论，结构的应力谱由传递函数和海浪谱生成。对于构成疲劳分析的海况来说，绝大多数为小振幅波，结构线性响应正比于波高，因此应力也遵从瑞利分布。应力分布的概率密度函数的生成，需要先求解应力的均方值，而应力的均方值可以从应力谱求得。

对于短期波浪引起的结构应力，为了避免计算程序上复杂的随机加载，可以采用等效应力的方法；而对于长期波浪统计，需要研究其加载次序。这两点便是本文讨论的主要内容。

1 应力谱及应力概率密度函数

1.1 海浪谱

波浪谱从频域角度描述波浪的组成，又称为频谱。海浪可视作由无限多个振幅不同、频率不同、方向不同、相位不同的波组成，在如图1所示的坐标系中[横轴为频率f，纵轴为Sηη(f)=H2/8，代表波浪的能量]表达这些波浪，便构成了波浪谱。

在海浪研究中对充分成长的风浪记录进行谱估计和曲线的拟合时，提出了多种谱，常见的有Pieron-Moskowitz(PM)谱和JONSWAP谱等。其中PM谱的定义如下[2]：

(1)

式中:Hs为有效波高;Tz为平均跨零周期。

图1 PM谱Fig.1 PM spectrum

1.2 应力谱及应力概率密度函数

根据结构随机振动理论，应力谱由应力传递函数G(f)的平方乘上频谱得到，传递函数为单位激励和结构响应之间的函数关系，表示为[2]

Sσσ(f)=|G(f)|2Sηη(f).

(2)

图2给出了这一方程的示意图。

应力的概率密度函数符合瑞利分布，其定义如下[2]：

(3)

式中：m0为应力谱的0阶矩,由前面应力谱的定义可知，m0的物理意义为应力均方值的1/8。

2 短期波浪引起的等效应力算法

2.1 等效应力的公式

有了应力谱和概率密度函数，下面考虑如何将其施加于结构并求解裂纹扩展。英国标准学会的BS7910(2005)8.4.2章对算法的建议是：把应力谱划分成一定数量的区块，区块的应力取其内部的最大值作为恒值，然后对每个区块分别进行计算，并且要选出造成最大裂纹扩展的区块加载次序[1]。

这种算法对于具有单一应力谱的结构是可行的；而对于生命周期为20～30年的海洋结构来说，应力谱的数量较大，加载次数多达上亿次，裂纹扩展公式的积分计算量是惊人的，因此需要寻找简化的方法。

应力作为随机变量，其多次作用的简化计算方法是求其等效值。这个等效也即对裂纹造成的扩展的等效，从数学上讲为所有应力的m次方的平均值。等效应力σe可由概率密度函数求出，计算公式如下：

(4)

假设此短期统计的持续时长为T，则应力循环次数为N=T/Te。

图2 应力谱的生成Fig.2 Generation of stress spectrum

2.2 考虑应力强度因子阈值影响时等效应力公式的修正

根据断裂力学理论，在应力强度因子变化幅Δk小于阈值Δk0时，不引起裂纹的扩展[1]，所以等效应力的计算要进行修正，过滤掉低应力部分。Δk0与材料、应力比R和环境有关。

(5)

有效循环次数修正为

(6)

在实际的计算程序中，可采用近似方法计算σe和Ne，方法如下。

把应力从应力幅阈值σ0到上限σu之间进行分解，步长为δσ。对每一个值σ，其出现概率为p(σ)·δσ，所以等效应力

(7)

有效循环次数

(8)

经过上述计算，最终得到裂纹扩展公式

(9)

2.3 积分上限σu的确定

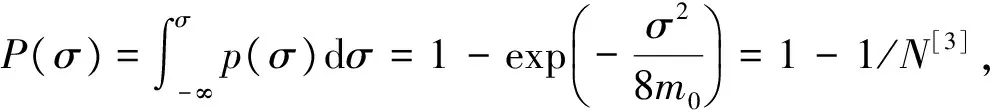
(10)

2.4 导管架管节点疲劳分析算例

下面以某导管架管节点的疲劳分析为例，展示求解等效应力的过程。为了计算简单，把传递函数进行了简化。

求解导管架的传递函数要进行确定性波浪响应分析，采用Airy波理论，波浪力用Morison方程计算。传递函数选取波浪周期从1～20 s之间的20～30个值，波陡采用1/25～1/20。为了求解某个波浪工况下的应力变化幅值δ，把波浪分成20个左右的不同的相位进行计算，20个相位中的最大值减去最小值即得到该工况的应力变化幅值[4]。

传递函数G(f)如图3所示，图中横坐标为频率，纵坐标为σ/H，H为对应某一频率的波高。

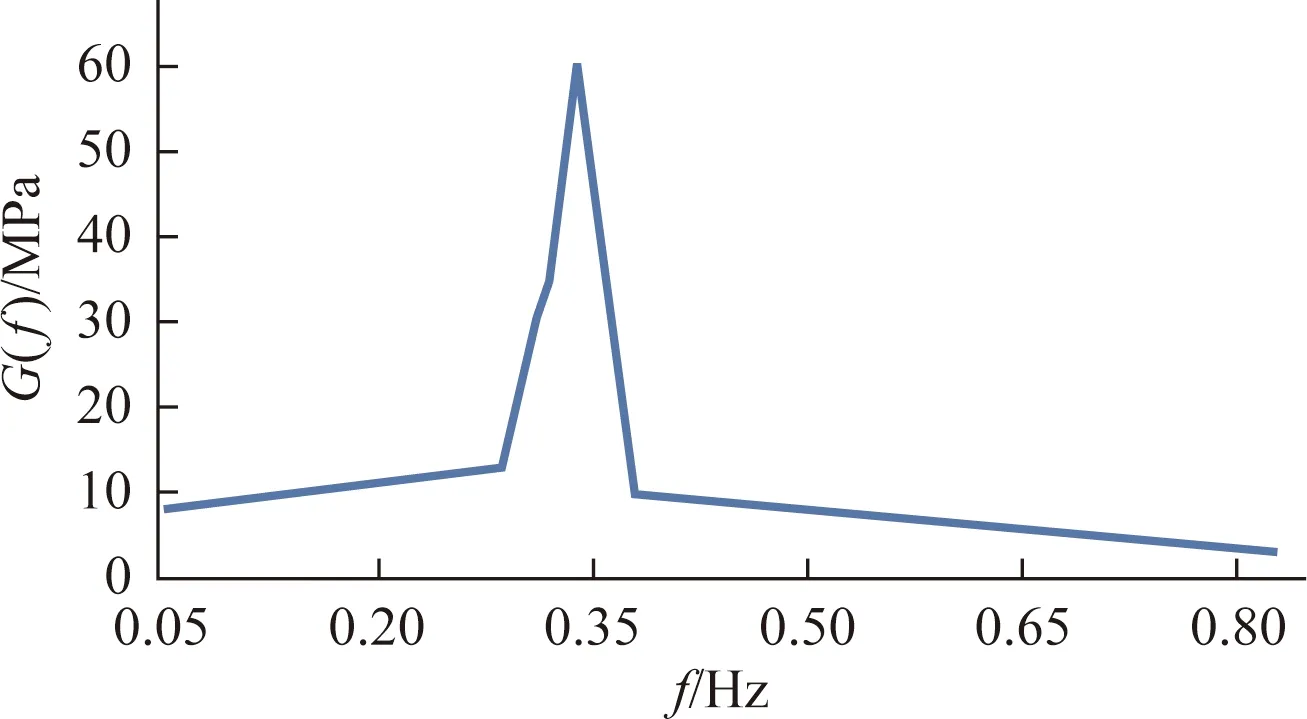
图3 传递函数Fig.3 Transfer function

表1给出了波浪数据和波浪谱；表2列出了根据式(2)和图3所示传递函数计算得到的应力谱的0阶矩、2阶矩和有效周期，应力谱的图形见图4；表3给出了裂纹参数；表4列出了根据2.2节公式计算得到的等效应力、循环次数以及裂纹扩展。

表1 波浪参数Table 1 Wave data

表2 应力谱Table 2 Stress spectrum

图4 应力谱Fig.4 Stress spectrum

表3 裂纹参数Table 3 Crack parameters

表4 裂纹扩展计算结果Table 4 Result for crack growth

3 波浪长期分布的加载顺序

3.1 加载次序的差别

注意到裂纹扩展率的公式是微分方程，裂纹扩展需要进行积分求解，每次加载的裂纹初始尺寸等于上次加载的最终尺寸，因此不同的施加次序可能会造成计算结果的不同。

波浪的长期统计是由“方向-Hs-Tz-出现概率”构成的表格，典型统计见表5；表格中的数据表示某个短期波浪的出现概率，其有效波高为Hs，跨零周期为Tz。在确定表中的波浪加载次序之前，我们首先要研究不同加载次序造成的差别。

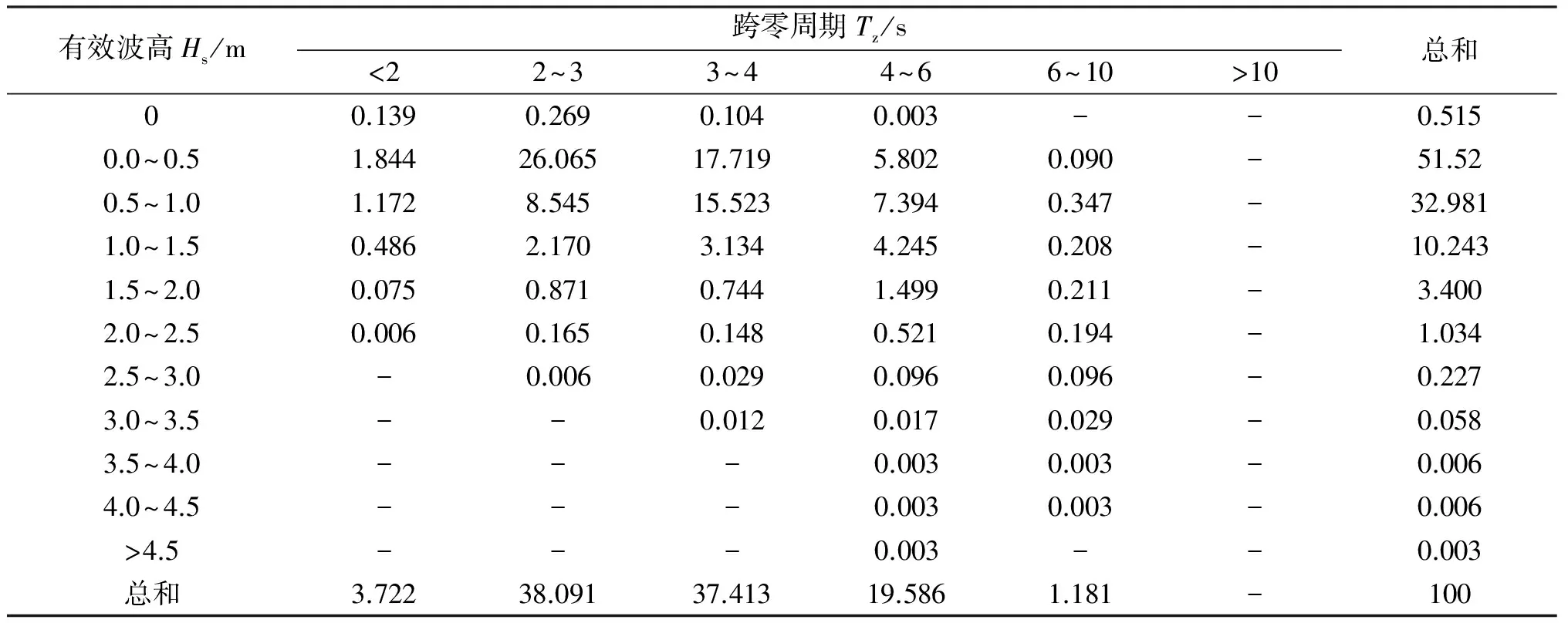
表5 典型波浪长期分布概率表Table 5 Typical long-term wave distribution

选取表6中所示6组波浪数据，用第2节的方法计算裂纹扩展，并对结果进行对比。应力传递函数仍然采用2.4节的数据，频谱采用PM谱。计算结果见表7。

表6 分组的波浪数据Table 6 Grouping of wave data

表7 裂纹扩展计算结果对比Table 7 Comparison of calculation results of crack growth

从表7的结果中可以看出，先施加较大荷载，后施加较小荷载，造成的破坏较大，但差别很小。

3.2 加载方法的确定

根据3.1节的结论，同时基于保守的原则，对于波浪长期概率分布表的数据，应采用从大波高到小波高的顺序进行施加。但是对于设计寿命为20～30年的海洋结构来说，这样做会与事实不符，因为在这么长的时间内实际波浪不会完全按照从大到小的顺序出现。

综合考虑安全、计算精度和计算量，对于波浪荷载的加载建议采用三级模式。第一级以年为单位，把总寿命划分成N块,记为Ti，这N块之间除给定裂纹初始尺寸的不同外无其他差别；如果事先总寿命不清楚，可以通过初步试算确定。

第二级为Ti的定义及分解，以3～24 h为单位，把Ti划分成m块，每块记为ti，每块ti有各自的有效波高Hs和跨零周期Tz；m个ti要符合波浪长期概率表的定义，并按照Hs由大到小的顺序施加到结构上。

第三级为每块ti内部，根据其Hs和Tz，采用第2节所述方法计算其等效应力和等效循环次数,作为裂纹疲劳评估的输入数据。

上述方法可用图5来表示。

图5 波浪加载算法图Fig.5 Numerical algorithm for wave loading

4 结 语

目前海洋结构疲劳分析常用的是应力-寿命(S-N) 曲线和断裂力学法。对于随机波浪的加载，S-N曲线的方法比较简单和成熟，而断裂力学方法的研究较少。这两种方法的主要区别就是等效应力的计算和加载次序。

在实际应用中，应力阈值σ0的计算比本文中公式要复杂得多，因为在应力强度因子的公式中，应力要分解为主应力、次应力、膜应力和弯曲应力，不同的应力有不同的修正因子Y。

同时应注意到，本文中应力谱的计算仅适用于线性反应体系，所以上述方法也仅适用于线性结构体系。在导管架的疲劳分析中，非线性的桩土基础可以进行近似的线性化，从而运用上述方法计算。

[1] British Standards Institution.BS 7910—2005.Guide to methods for assessing the acceptability of flaws in metallic structures [S].2005.

[2] Barltrop N D P.Dynamics of Fixed Marine Structures[M].Oxford: Butterworth-Heinemann,2011: 609-635.

[3] 刘永庚.海洋工程水动力学[M].北京：国防工业出版社，2012：19-49.

[4] American Petroleum Institute.API RP 2A-2007.Recommended practice for planning,designing and constructing fixed offshore platforms—working stress design[S].2007.

ResearchofNumericalAlgorithmsforStructure’sFatigueAssessmentinRandomWavesBasedonFractureMechanics

YIN Yan-kun,CHEN Shi,LI Ting-qian

(ZhanjiangNanhaiWestOilSurveyamp;DesignCo.,Ltd.,Zhanjiang,Guangdong524057,China)

Paris law gives a simple formula for offshore structure’s fatigue assessment with fracture mechanics method.However,the input “stress” data are complex,because the offshore structure’s response under random waves is complex.For structures exposed under long-term waves,it is important to find a numerical algorithm which is efficient,accurate and safe for calculating fatigue life.Structure’s response stress is a random variable,so its equivalent constant value can be investigated for efficiency，and its loading sequence under long-term waves should be investigated for conservation.

random waves; fracture mechanics; fatigue; numerical algorithm

TU973+.254

A

2095-7297(2014)03-0213-05

2014-08-20

尹彦坤(1980-)，男，高级工程师，主要从事海洋石油固定式平台结构设计。