改进的最大最小特征值之差的频谱感知算法

赵知劲，胡伟康

(杭州电子科技大学 通信工程学院，浙江 杭州 310018)

认知无线电CR(Cognitive Radio)[1]允许认知用户SU(Secondary User)利用授权主用户PU(Primary User)的空闲频段进行通信，可以提高频谱利用率，而频谱感知是认知无线电的关键技术之一。目前，频谱感知方法主要有循环平稳特征检测、匹配滤波器检测和能量检测ED(Energy Detection)等方法。但是这些经典频谱感知方法都有各自特定的应用场合和缺陷[2]，例如需要预先知道PU的先验信息，对噪声的不确定性敏感等。

针对上述缺陷，利用随机矩阵理论RMT(Random Matrix Theory)的频谱感知技术引起国内外学者的关注，迅速成为当前的研究热点，提出了多种基于RMT的频谱感知算法。参考文献[3]提出了最大最小特征值MME(Maximum Minimum Eigenvalue)算法，参考文献[4]提出了最大最小特征值之差DMM(Difference between Maximum and Minimum eigenvalue)算法，DMM比MME具有更好的检测性能。但在协作用户较少的情况下，DMM性能有待提高，对此，本文提出了改进的DMM算法，对感知信号进行拆分重组，增加协作用户的逻辑个数，提高了DMM算法在较少协作用户情况下的性能。

1 理论基础

考虑多径衰落信道下的频谱感知，h(n)代表了发射机与接收机之间的信道衰落函数，则SU采样信号x(n)=h(n)s+w(n)=s(n)+w(n)，s代表 PU 发射信号，s(n)代表发射信号经过信道衰减后接收到的信号，w(n)是加性高斯白噪声。假设感知过程中有M个SU，每一个SU对接收信号采样N次，则第i个SU在k时刻的采样信号、接收信号及噪声分别表示为 xi(k)、si(k)和 wi(k)。

定义M×N维采样信号向量矩阵X=[x1x2… xM]T,其中,xi=[xi(1)xi(2)… xi(N)]T(i=1,2,…,M)表示第 i个SU采样得到的信号向量。相应的定义背景噪声向量矩阵为W，PU发射信号经过信道衰减后接收到的信号向量矩阵为S。频谱感知过程可以看作为一个二元假设检验过程，SU对PU发射机信号进行检测的结果存在两种可能，建立假设检验模型如下：

假设噪声W是均值为0、方差为σ2的高斯白噪声。当PU发射信号不存在时，S为 0，则式(1)可以统一表示为X=S+W。根据PU发射信号与噪声统计独立，可得接收信号的统计协方差矩阵为：其中,IM为单位矩阵。定义如下采样协方差矩阵：

假设信号与噪声是平稳遍历，则当N→∞，可以得到如下关系式，,即当 N→∞ 时，信号协方差矩阵的统计平均等于采样平均。当PU发射信号不存在时，此时噪声协方差矩阵为Wishart随机矩阵，该随机矩阵的联合概率密度函数表达式非常复杂，但是根据参考文献[5-6]，其最大最小特征值的特性可由如下定理描述。

2 改进的DMM频谱感知算法

2.1 检验统计量的确定及判决准则[4]

将TDMM作为判决统计量，判决门限设为γDMM，算法性能取决于γDMM的设置。根据以上分析，DMM算法的判决准则为：

(1)当 TDMM≥γDMM时，检测到 PU信号，判决H1成立；

(2)当 TDMM＜γDMM时，未检测到 PU信号，判决 H0成立。

2.2 IDMM算法

基于定理1和定理 2，DMM算法的虚警概率Pf可以表示为：

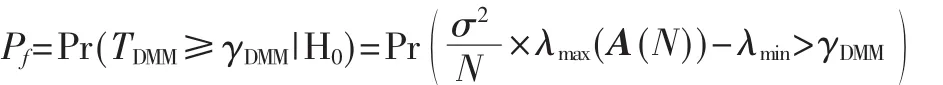
因此，DMM算法的理论门限值为:

可得DMM算法的门限与噪声σ2有关。根据随机矩阵理论，估计噪声方差

由于DMM算法的检测统计量TDMM和门限值γDMM都与信号自相关矩阵的最大特征值和最小特征值估计有关，最大特征值和最小特征值由PU信号的最大特征值ρmax和噪声方差σ2决定，而 ρmax和σ2的估计又与协作用户数M和采样点数N有关,协作用户数M和采样点数N越多，能够获得的信号信息越多，对 ρmax和σ2估计越准确，因此检测性能越好。

基于上述分析，在采样点数N和协作用户数M一定的情况下，本文将信号拆分成多个子信号，在总的数据量不变的前提下，增加了用户的逻辑个数，以获得更多的信号相关信息，提高DMM算法在较少协作用户情况下的性能，提出了IDMM算法。

在 IDMM 算法中，将 xi(i=1,2,…,M)拆分成 q(q＞0)段k=N/q长的子信号向量，将拆分后的信号向量进行重组，则可以得到一个(qM)×k维的信号矩阵Y:

第1节中的定理1与定理2成立的前提是相比于协作用户数M，采样点数N趋向于无穷大，即N远大于M。为了在IDMM算法中能继续应用上述定理，对矩阵Y定义如下限制：拆分后的信号矩阵需满足k＞＞qM。

将上述拆分后的矩阵Y表示成向量形式Y=S′+W′，其中 S′=[s11,…，sjm,…,sMq]T,W′=[w11,… ，wjm,…,wMq]T。 对于矩阵 Y，任取两个向量xim，xjn做相关检测，则有:

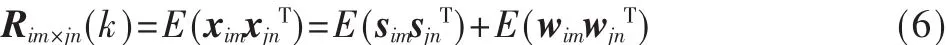
当j=i,m=n时,此时为自相关检测;不相等时为互相关检测，此时 Rim×jn(k)=E(wimwjnT)。互相关检测消除了噪声的自相关性对信号的影响,其性能要优于自相关检测。

Y 的协方差矩阵 RY＝E(YYT)=E(S′S′T)+E(W′W′T)=Rs′+σ2IqM， 定义矩阵 Y 的采样协方差矩阵=YYT/k，当k→∞时，信号协方差矩阵的统计平均等于采样平均RY=(k)。

综上所述，IDMM算法主要步骤如下：按照式(5)，对xi(i=1,2,…,M)进行拆分重组，获得(qM)×k 维矩阵 Y；对矩阵R^Y(k)进行特征值分解，求得最大最小特征值，得到判决统计量 TDMM=λmax-λmin；估计噪声方差，由式(4)计算得到门限γDMM；最后根据判决准则进行检测。

3 算法仿真及结果分析

本节仿真分析算法性能，主用户信号采用经过升余弦脉冲成型的QPSK调制信号。假设用户数M=4，虚警概率Pf=0.05，5 000次的M-T模拟仿真各种算法。图1是不同q值情况下门限γDMM随采样点数N变化的理论值与仿真值曲线。从图可见随着采样点数N的增加，理论值与仿真值都趋于稳定。因为对门限值的理论推导过程中，最小特征值采用的是极限值，导致门限γDMM的理论值与仿真值有一定偏差，但是随着采样点数的增加，最小特征值逐渐逼近理论值，因此γDMM理论值与仿真值的偏差也越来越小，这与图1中随着N的增加，理论值与仿真值的曲线接近重合是一致的。表1是当采样点数N为8 500次时，不同q值情况下的理论门限值与仿真门限值，从表1中可以得到，当采样点数足够大时，门限仿真值近似等于理论值，且随着q值的增加，两者之间的偏差越来越小，验证了算法理论分析的正确性。

图1 门限仿真值与理论值

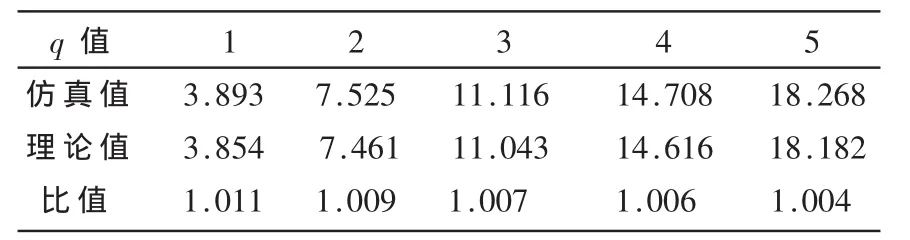
表1 N=8 500门限理论值与仿真值

当采样点数 N=3 000，q 值分别取 2、3、4、5 时，算法的检测性能如图2所示。 由图2可见，随着q值的增加，检测性能逐步提高。例如当信噪比为-15 dB时，DMM算法的检测概率为0.3，而4次拆分后的IDMM算法检测概率达到了1。上述结果验证了算法理论分析的正确性，充分表明了IDMM算法的优越性。进一步分析图2可以看出，当q值再增加时，检测性能提高幅度越来越小。这与理论分析是相符的，在式(5)中对拆分后的矩阵Y定义过k>>qM的限制条件，所以拆分次数有限的，当拆分次数超过一定范围后，不能继续应用定理1和定理2的结论。

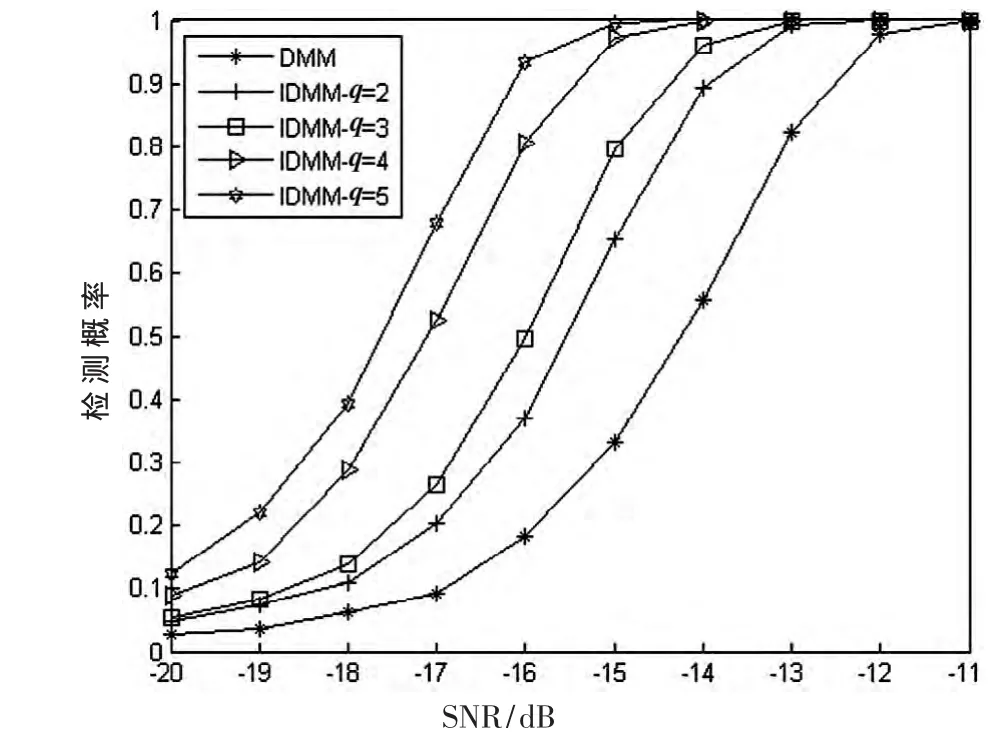
图2 不同q值下IDMM算法检测概率

下面对不同算法的检测性能进行比较，在IDMM算法中，q取2。由于ED算法与噪声不确定性有关，为了便于比较，假设σ2=1固定不变，采样点数N=3000，4种算法的检测概率与信噪比之间的关系如图3所示。由图可见，随着信噪比的增加，4种算法的性能均有提高，但IDMM算法的检测性能明显优于其他3种检测算法。

本文从提高特征值估计精度出发，根据DMM算法的理论基础，对接收信号矩阵拆分重组，提出了IDMM算法。理论分析与实验仿真均表明，该算法延续了DMM算法优点，即感知性能不受噪声不确定度的影响，无需知道主用户的信息，同时检测性能优于DMM算法，而算法复杂度与DMM算法相同。

图3 4种算法性能比较

[1]MITOLA J,MAGUIRE G Q.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):13-18.

[2]李转,任旭虎.基于信任度函数的认知无线电频谱感知算法研究[J].电子技术应用,2012,38(6):108-114.

[3]Zeng Yonghong,Liang Yingchang.Eigenvalue-based spectrum sensing algorithms for cognitive radio[J].IEEE Transactions on Communications,2009,57(6):1784-1793.

[4]王颖喜,卢光跃.基于最大最小特征值之差的频谱感知技术研究[J].电子与信息学报,2010,32(11):2571-2575.

[5]JOHANSSON K.Shape fluctuations and random matrices[J].Communications in Mathematical Physics,2000,209(2):437-476.

[6]JOHNSTONE I M.On the distribution of the largest eigenvalue in principle components analysis[J].The Annals of Statistics,2001,29(2):295-327.