弹头引信外形对小口径亚音速弹气动特性影响*

王洪超，闻 泉，刘治旺，王雨时，张树明

(1南京理工大学机械工程学院，南京 210094;2湖南建华精密仪器有限公司，湖南永州 425024)

0 引言

弹丸外形直接影响其空气动力特性、有效载荷和威力［1］。轻武器领域中的小口径弹丸多配用弹头引信，并且弹头引信的形状即为弹丸的头部形状。美国引信头部多为半球形，如 M550、M549和 F/M918等［2］;俄罗斯引信头部多为单一圆台形，如ВОГ-17和B429Э等［3］;目前我国轻武器领域中的小口径弹丸引信头部形状多为组合圆台形。表1为中、美、俄三国小口径榴弹引信外形和弹道参数。

关于不同弹头引信外形对弹丸气动特性影响研究国内外均未见报道。国内众多文献运用FLUENT软件主要研究了不同类型弹丸的气动特性，如秦豪等［4］研究了处于简易制导状态下的某型弹道修正弹在不同攻角、不同飞行马赫数下的气动力特性;王晓兵等［5］研究了用仿真方法设计弹丸气动外形的可行性;胡志鹏等［6］研究了S-C形尾翼组合的末敏弹气动特性;吴志林等［7］研究了微型修正弹药的气动特性。

表1 中、美、俄小口径榴弹引信相关参数［2-3］

文中采用FLUENT软件对三种不同引信头部形状弹丸在不同马赫数(Ma＜1)、不同攻角下(α＜16°)的气动特性进行仿真分析，得到这三种弹丸的阻力系数、升力系数、俯仰力矩系数和压力中心随马赫数和攻角的变化规律。对比分析这三种弹丸的气动特性以得到其中最佳的气动外形，从而为弹丸和引信总体方案设计提供参考。

1 数值模型

1.1 弹丸有限元模型

方案A引信头部形状为单一圆台形，如图1所示。弹长L为108 mm，直径D为35 mm，H为34.7 mm，d为16.4 mm。

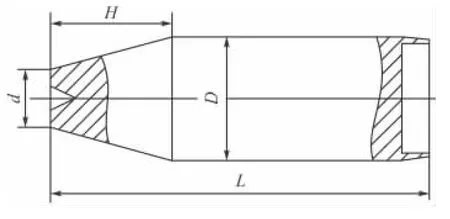
图1 引信头部形状为单一圆台形的弹丸

方案B引信头部形状为组合圆台形，如图2所示。H1为36 mm，H2为 6.6 mm，H3为 27.7 mm，H4为5.7 mm，d1为21.6 mm，d2为 21 mm，α1为 40°，α2为 30°，α3为16°。

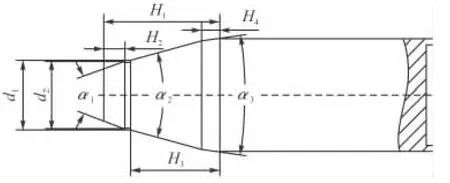
图2 引信头部形状为组合圆台形的弹丸

方案C引信头部形状为半球形，如图3所示。

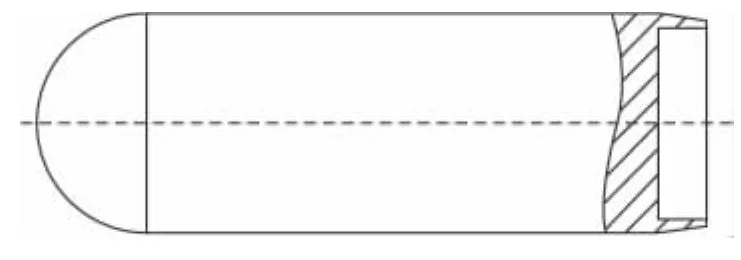
图3 引信头部形状为半球形的弹丸

三种弹丸弹径和弹长相同。由于研究的是弹丸外流场，所以建立直径和长度均是弹丸直径和长度20倍的圆柱体来模拟弹丸外部流场，避免边界反射引起空气流场中的压力计算不稳定。弹丸置于空气流场计算域中心位置，假设弹丸表面为绝热壁，弹丸附近网格加密以准确获得阻力系数、升力系数和俯仰力矩系数。

1.2 初始条件与边界条件

所研究的马赫数和攻角情况都属于定常流动范围，采用相对运动条件模拟弹丸附近外流场，即假设弹丸静止、来流为理想气体，选择萨兰德定律计算气体粘性，空气以反向相同速度流动，计算域边界条件设置为远场压力条件，湍流模型采用S-A(Spalart-Allmaras)模型［8］。由于求解的是可压缩气体，涉及总压和静压等多种压力，所以为便于设置边界条件和计算结果的后处理，将参考压力置为零［9］。

1.3 气动特性求解

弹丸阻力与产生阻力的面积、飞行速度、飞行高度和攻角有关。为了说明阻力特性，用单位面积和单位动压条件下产生的压力即阻力系数表示［10］:

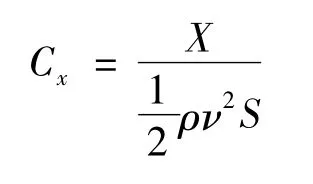
式中:X为阻力;ρ为空气密度;v为气流相对于弹丸的流速;S为参考面积，在此取为弹丸最大横截面积。

与阻力系数相似，升力系数Cy与升力Y之间的关系可表示为:

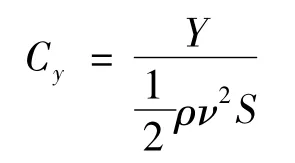
式中Y为升力。

作用于弹丸上的空气动力合力的作用点称为压力中心。所研究的弹丸压力中心通过纵轴线。压力中心可表示为压力中心到弹头的距离x与弹长L的比值。

作用于弹丸上的气动力作用点不通过弹丸质心，由此会产生绕质心的力矩。俯仰力矩系数为:

式中Mz为俯仰力矩。

2 仿真结果

计算三种弹丸在来流马赫数分别为0.20、0.40、0.60、0.80、0.85、0.90 和 0.95，攻角为 α =0°、4°、8°、12°、16°时的空气流场，得到相关阻力系数、升力系数和俯仰力矩系数参数。

2.1 阻力特性

图4～图 8 分别为攻角在 0°、4°、8°、12°、16°时三种弹丸阻力系数随马赫数变化曲线图。

在马赫数小于0.7时，头部形状为半球形的弹丸阻力系数最小，头部形状为单一圆台形的弹丸阻力系数最大。马赫数大于0.7时，头部形状为组合圆台形的弹丸阻力系数最小，头部形状为半球形的弹丸阻力系数最大。攻角小于4°时，攻角对于三种方案阻力系数随马赫数的变化趋势基本没有影响。攻角大于4°、马赫数小于0.6时，随着攻角的增大，三种方案在相同攻角时的阻力系数差距变大;在攻角大于4°、马赫数大于0.6时，攻角对三种方案阻力系数随马赫数的变化趋势基本没有影响。

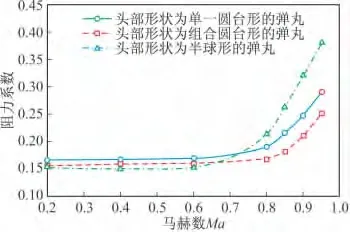
图4 攻角0°时三种方案阻力系数随马赫数变化曲线

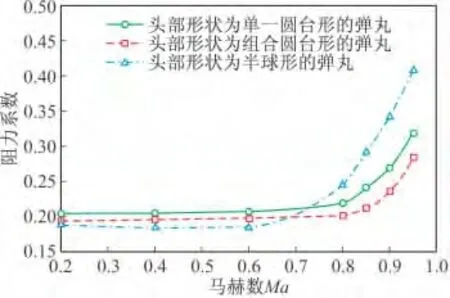
图5 攻角4°时三种方案阻力系数随马赫数变化曲线

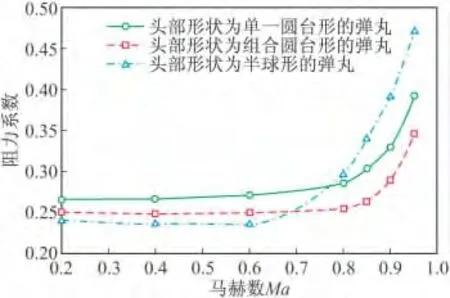
图6 攻角8°时三种方案阻力系数随马赫数变化曲线

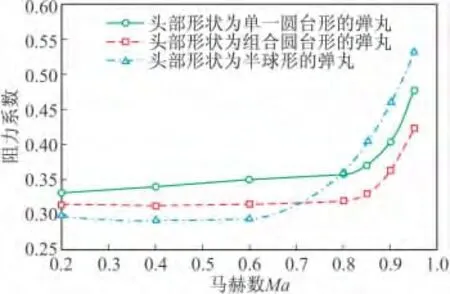
图7 攻角12°时三种方案阻力系数随马赫数变化曲线

图8 攻角16°时三种方案阻力系数随马赫数变化曲线

阻力系数 Cx主要是 Ma和 α的函数，据文献［11］知，当α不大且在不跨音速时有:

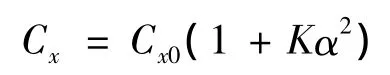
式中α的量纲为rad。

以头部形状为组合圆台形的弹丸为例，通过Matlab软件拟合0.2 Ma下Cx随攻角变化曲线，得曲线方程:

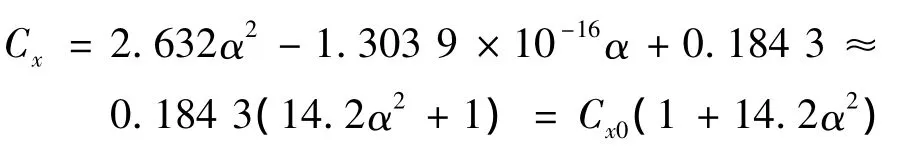
得K0.2Ma=14.2。方程中α的一次项系数极小，因此可以忽略α的一次项。同理可以得到三种方案在Ma=0.2，0.4，0.6，0.8，0.85，0.9，0.95 下弹丸攻角系数如表2所列，图9为三种方案攻角系数随马赫数变化曲线。

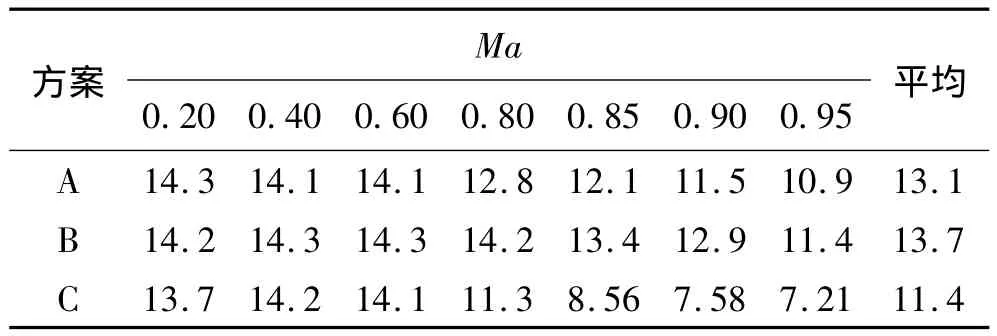
表2 三种方案攻角系数随马赫数变化值

图9 三种方案攻角系数随马赫数变化曲线

结合表2和图9可得:在马赫数小于0.6时，三种方案攻角系数的差异很小，在马赫数大于0.8时，三种方案攻角系数各自随着马赫数的增大而减小，头部形状为半球形的弹丸减小的速度更大，头部形状为单一圆台形的弹丸次之，头部形状为组合圆台形的弹丸最小。

2.2 升力特性

图10～图13分别为攻角在 4°、8°、12°、16°时三种弹丸升力系数随马赫数变化曲线。攻角为0°时，升力系数为零。在马赫数小于0.8时，头部形状为半球形的弹丸升力系数最大，头部形状为单一圆台形的弹丸升力系数最小;在马赫数大于0.8、攻角小于4°时，头部形状为单一圆台形的弹丸升力系数最小;在马赫数大于0.8时，头部形状为组合圆台形的弹丸升力系数最大。

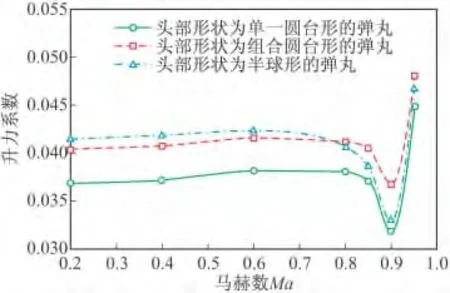
图10 攻角4°时三种方案升力系数随马赫数变化曲线

图11 攻角8°时三种方案升力系数随马赫数变化曲线

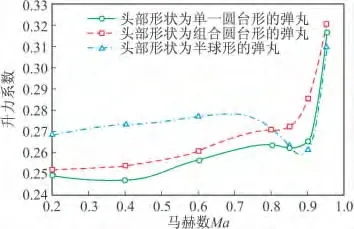
图12 攻角12°时三种方案升力系数随马赫数变化曲线

图13 攻角16°时三种方案升力系数随马赫数变化曲线

2.3 俯仰力矩系数特性

图14～图 17 分别为攻角在 4°、8°、12°、16°时三种弹丸俯仰力矩系数随马赫数变化曲线。攻角为0°时，俯仰力矩系数为零。在攻角小于4°时，头部形状为半球形的弹丸俯仰力矩系数最大，头部形状为组合圆台形弹丸的俯仰力矩系数最小;在攻角大于4°时，头部形状为半球形弹丸的俯仰力矩系数最大，头部形状为单一圆台形弹丸的俯仰力矩系数最小。

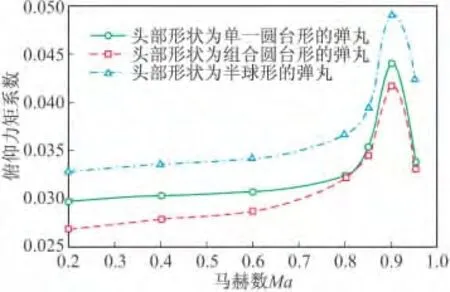
图14 攻角4°时三种方案俯仰力矩系数随马赫数变化曲线

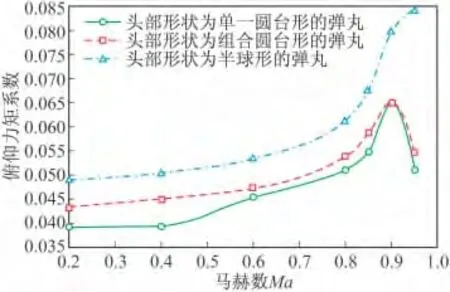
图15 攻角8°时三种方案俯仰力矩系数随马赫数变化曲线

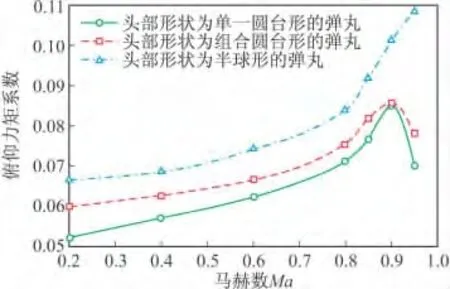
图16 攻角12°时三种方案俯仰力矩系数随马赫数变化曲线

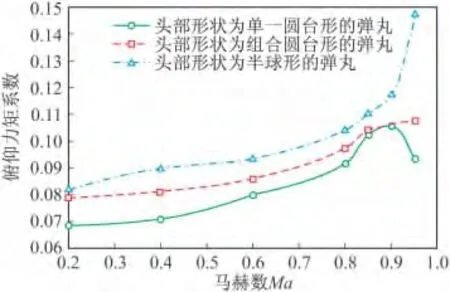
图17 攻角16°时三种方案俯仰力矩系数随马赫数变化曲线

2.4 压力中心变化特性

如图18～图22为三种方案在不同攻角下压力中心随马赫数变化曲线，半球形弹丸压力中心最小，头部形状为单一圆台形的弹丸次之，头部形状为组合圆台形的弹丸最大。在马赫数小于0.6时，压力中心基本不变;在马赫数大于0.6、攻角小于12°时，头部形状为单一圆台形的弹丸和头部形状为组合圆台形的弹丸压力中心随着马赫数的增大而缓慢增大，头部形状为半球形的弹丸压力中心随着马赫数的增大而缓慢减小;在马赫数大于0.6、攻角大于12°时，头部形状为单一圆台形的弹丸、头部形状为组合圆台形的弹丸和头部形状为半球形的弹丸压力中心随着马赫数的增大而缓慢增大。头部形状为组合圆台形的弹丸和头部形状为半球形的弹丸压力中心相近，比头部形状为半球形的弹丸压力中心大，因此前两种方案更稳定，精度更高。

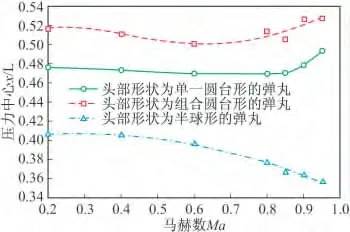
图18 攻角0°时三种方案压力中心随马赫数变化曲线

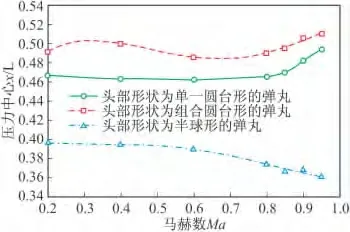
图19 攻角4°时三种方案压力中心随马赫数变化曲线

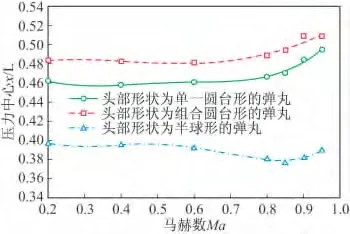
图20 攻角8°时三种方案压力中心随马赫数变化曲线

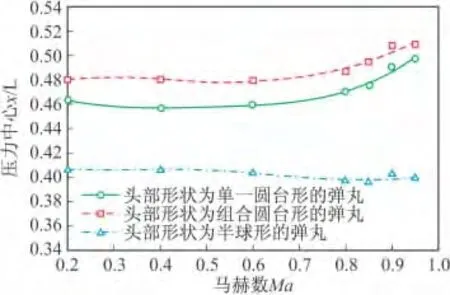
图21 攻角12°时三种方案压力中心随马赫数变化曲线

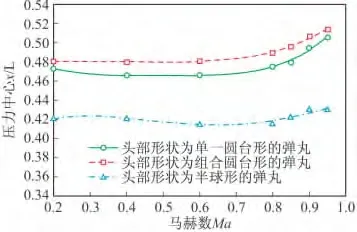
图22 攻角16°时三种方案压力中心随马赫数变化曲线

3 仿真结果验证

已知头部形状为组合圆台形的弹丸根据全射程反推出的平均弹形系数i43=1.26(简称工程值)。表3对比地给出了0°攻角下阻力系数仿真值与由此弹形系数(工程值)得到的阻力系数。现仿真值比工程值平均低4.7%，如果考虑到实际弹道攻角不可能为0的系统性影响，则可以认为仿真结果是较为可信的。

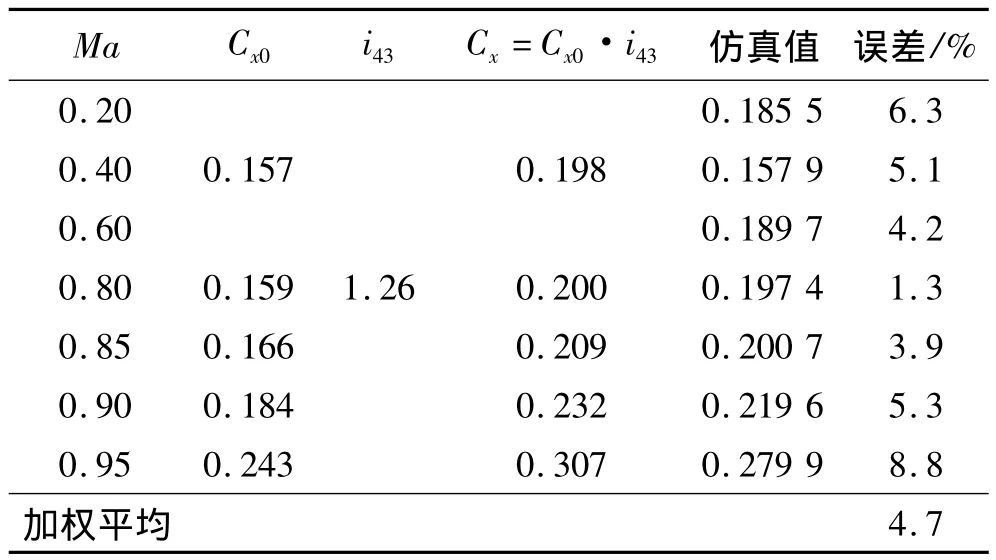
表3 仿真值与阻力定律对比［12］

4 结论

a)当马赫数小于0.7时，头部形状为半球形的弹丸阻力系数最小，头部形状为组合圆台形的弹丸次之，头部形状为单一圆台形的弹丸最大;当马赫数大于0.7时，头部形状为组合圆台形的弹丸阻力系数最小，头部形状为单一圆台形的弹丸次之，头部形状为半球形的弹丸最大。攻角对于三种方案阻力系数随马赫数变化曲线影响不大。在马赫数小于0.6时，三种方案攻角系数的差异很小，在马赫数大于0.8时，三种方案攻角系数各自随着马赫数的增大而减小，头部形状为半球形的弹丸减小的速度最大，头部形状为单一圆台形的弹丸次之，头部形状为组合圆台形的弹丸最小，即头部形状为半球形的弹丸阻力特性受攻角影响最小，特别是在接近音速时。

b)当马赫数小于0.8时，头部形状为半球形的弹丸升力系数最大，攻角对于三种方案升力系数随马赫数变化曲线影响不大;当马赫数大于0.8时，头部形状为组合圆台形的弹丸升力系数最大。

c)在攻角小于4°时，头部形状为半球形的弹丸俯仰力矩系数最大，头部形状为单一圆台形的弹丸次之，头部形状为组合圆台形的弹丸最小;在攻角大于4°时，头部形状为半球形的弹丸俯仰力矩系数最大，头部形状为组合圆台形的弹丸次之，头部形状为单一圆台形的弹丸最小。

d)头部形状为半球形的弹丸压力中心最小，头部形状为单一圆台形的弹丸次之，头部形状为组合圆台形的弹丸最大。由此推断头部形状为半球形的美国40 mm榴弹长径比之所以比较小，可能是受制于飞行稳定性和精度要求。而与此相反，头部形状为组合圆台形的我国35 mm榴弹长径比则较大。在马赫数小于0.6时，三种弹丸压力中心变化很小;在马赫数大于0.6、攻角小于12°时，头部形状为单一圆台形的弹丸和头部形状为组合圆台形的弹丸压力中心随着马赫数的增大而缓慢增大，头部形状为半球形的弹丸压力中心随着马赫数的增大而缓慢减小;在马赫数大于0.6、攻角大于12°时，头部形状为单一圆台形的弹丸、头部形状为组合圆台形的弹丸和头部形状为半球形的弹丸压力中心随着马赫数的增大而缓慢增大。

e)由文献［2］可知，美国40 mm口径高速榴弹初速为242 m/s，约为0.7 Ma，低速榴弹初速为76 m/s，约为0.2 Ma，头部形状为半球形的弹丸在小于0.7 Ma飞行时的阻力系数最小，且弹丸容腔较大，有利于弹丸优化设计与威力提高。因此可以说美国40 mm口径榴弹是一种最优设计。

f)我国35 mm口径杀伤破甲弹设计初速为320 m/s，约0.95 Ma，头部形状为组合圆台形的弹丸在0.7～0.95 Ma区间飞行时的阻力系数最小。因此可以说我国35 mm口径榴弹也是一种低阻优化设计。

［1］韩子鹏.弹箭外弹道学［M］.北京:北京理工大学出版社，2008.

［2］中国兵工学会引信专业委员会.美国军用手册:现役引信概览［M］.西安:中国兵工学会引信专业委员会，2000.

［3］《俄罗斯新兵器手册》编辑部.俄罗斯新兵器手册［M］.北京，兵器工业出版社，1998.

［4］秦豪，马少杰.基于FLUENT的弹道修正弹制导状态气动仿真［J］.四川兵工学报，2010，31(7):30-32.

［5］王晓兵，李菁，廖忠全，等.基于FLUENT的弹丸外流场数值仿真［J］.计算机辅助工程，2010，19(1):92-94.

［6］胡志鹏，刘荣忠，郭锐.基于FLUENT的双翼末敏气动特性研究［J］.飞行力学，2013，31(1):53-56.

［7］吴志林，陶家宾.基于FLUENT的微型修正弹药气动特性仿真［J］.计算机仿真，2013，30(6):20-23.

［8］郑健，周长省，鞠玉涛，等.Spalart-Allmaras湍流模型在弧形翼超音速流场数值模拟中的应用［J］.重庆工学院学报，2008，22(12):34-39.

［9］于勇.FLUENT入门与进阶教程［M］.北京:北京理工大学出版社，2008.

［10］赵育善，吴斌.导弹引论［M］.西安:西北工业大学出版社，2009.

［11］浦发，芮筱亭.外弹道学［M］.修订本.北京:国防工业出版社，2008.

［12］徐明友.火箭外弹道学［M］.北京:兵器工业出版社，1989.