鸭舵修正机构舵偏角选择方法*
2014-12-10郭煜洋郝永平
邵 盼,郭煜洋,郝永平,张 华
(沈阳理工大学兵器科学技术研究中心,沈阳 110159)
0 引言
目前精确打击弹药在信息化战争中有着非常重要的作用,其中二维弹道修正弹成本较低并具有一定的打击精度,而修正能力是保证打击精度的基础。二维弹道修正的方式主要分为鸭舵修正和微小型推进器修正,其中微小型推进器修正对弹丸的修正能力次数是有限的,并且在引信中集成的难度系数很大,而鸭舵修正能对弹丸实施较为平稳的修正,修正能力连续灵活,且可以对较长飞行时间的弹丸弹道进行修正,是目前二维弹道修正技术的主要方法。
文中以某普通制式弹丸为研究对象,使用固定式鸭舵对其进行二维弹道修正。首先分析了不同舵偏角下弹丸的气动特性,并运用ADAMS仿真得到不同舵偏角下的弹丸飞行稳定性特征,综合考虑电机控制能力和修正能力得出合理选择鸭舵舵偏角的方法。
1 固定式鸭舵修正弹修正方法
鸭舵式二维弹道修正弹的修正机构主要包括舵翼、探测系统、控制系统、引信激发装置等,修正执行机构主要是两对带偏角的舵翼,其中一对是减旋舵,另一对是修正舵。当减旋舵受到空气动力作用时,导致引信的导转力矩与原旋转方向相反,为控制引信提供部分动力。当需要修正偏移量时,修正舵会提供所需的气动力。可见修正舵对弹丸的修正效果有很大的影响,而不同的舵偏角又对舵片的选择具有重要的意义,所以合理的舵偏角是保证弹道修正弹打击精度的必要条件之一。二维弹道修正原理如图1所示:当需要打击某一目标时,在弹丸发射前将目标落点的相关参数输入到二维弹道的修正引信中,弹丸发射后,引信中的弹载系统结合弹丸的发射初始条件和目标参数,计算出理论弹道;在弹丸飞行过程中,弹丸的实时飞行参数传给弹丸的探测装置,弹载系统对此进行计算得到实际弹道,并与理论弹道的相关数据进行比较,对弹道进行俯仰和偏航修正。当偏差达到预先设置的修正量极限时,控制系统就会利用修正机构对弹道进行修正,从而可以更好的导向目标落点,实现提高打击精度、高效毁伤目标的目的。
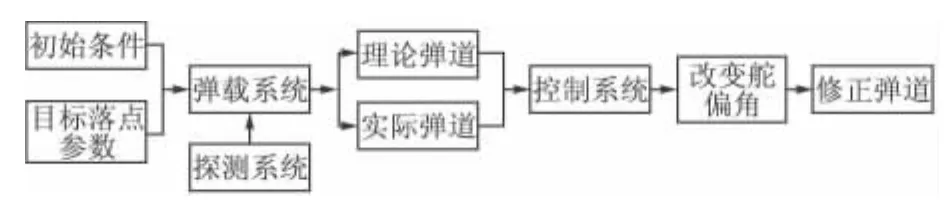
图1 鸭舵式二维弹道修正弹修正系统原理图
2 不同舵偏角气动特性分析
二维修正弹的修正鸭舵迎风面积相同,舵偏角度数不同时对弹丸的气动特性是有影响的,而且不同的偏角度数对弹丸的整体气动特性的影响也是不同的,直接影响着舵翼的侧向力、导转力矩和整个弹丸的阻力、翻转力矩等方面,可能会使弹丸在飞行过程中出现翻转、过稳定等情况,影响弹丸的打击能力,故选择合理的舵偏角同样是保证弹丸修正机构气动布局设计合理的重要条件。
为了观察鸭舵式二维弹道修正舵偏角对全弹气动特性的影响,以确定合理的舵偏角。在此以某炮弹为研究背景设计了舵翼迎风面积、形状、位置等相同,舵偏角不同的仿真模型,其中弹丸布局如图2所示。

图2 鸭舵机构与全弹布局简图
现建立以非对称舵为例,分别取舵偏角2°、4°、6°、8°、10°、12°、14°的仿真模型进行气动仿真,得到图3~图5的结果。
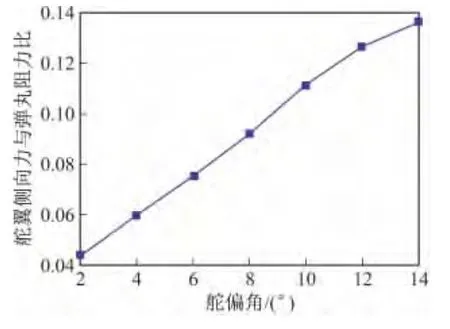
图3 舵偏角大小对舵翼侧向力与弹丸阻力之比影响
从图3中可以看出,舵翼侧向力与弹丸阻力的比例关系是随着舵偏角的增加而有增大趋势的,其中2°~8°偏角时,比例关系基本呈线性关系。
从图4可以看出,弹丸翻转力矩随舵偏角的增大而增加,其中2°~12°偏角时,比例关系基本呈线性关系,舵偏角增加的幅度比较大,这对弹丸的稳定性影响比较大。

图4 翻转力矩与舵偏角关系

图5 舵翼导转力矩与舵偏角关系
从图5中可以看出,舵翼导转力矩随着舵偏角的增加呈线性关系增加,由于引信部分的转动惯量一定,当导转力矩越大则引信旋转的速度越快,对电机的要求越高。若选择的舵偏角过大,则会因无法选择合适的电机而不能实现弹丸的合理设计。
以2°、6°、10°舵偏角时的压力等值线图为例,如图6比较可以看出:不同的舵偏角所展现出的弹丸周围云图有明显差异。

图6 数值模拟仿真
从以上分析可以看出,舵偏角对弹丸的舵翼升力、舵翼导转力矩、弹丸翻转力矩影响是非常明显的,其中舵偏角越大弹丸舵翼的升力、导转力矩以及弹丸的翻转力矩越大。
3 边力学仿真分析
以某普通制式弹丸为基础的修正弹,在射角50°,初速800 m/s等初始条件下,基于动力学分析软件,结合弹丸在飞行过程中,受静不稳定力矩的作用,在扰动产生攻角及弹丸在重力作用下弹道出现弯曲等的影响。通过动力学仿真分析,得到不同舵偏角下修正弹丸的实时运动状态。其中舵偏角在6°及以下时弹丸均能克服上述影响,从而满足陀螺稳定性、动态稳定性、追随稳定性,进行稳定的全弹道飞行,而在8°偏角时则修正弹丸无法完成稳定的全弹道飞行。其中部分偏角下的弹丸飞行状态动态情形如图7、图8所示。

图7 6°舵偏时弹丸稳定运动姿态

图8 8°舵偏时弹丸不稳定运动状态
通过动力学仿真可以观察到,当舵偏角为6°时,修正弹丸的外弹道飞行是稳定的。舵偏角达到8°时,修正弹丸的飞行状态是不稳定的,出炮口后弹丸很快出现翻转。同理,可以知道当舵偏角大于8°时,修正弹丸的飞行是不稳定的。
4 电机控制能力分析
固定在弹丸头部位置的鸭舵,包含一对减旋舵和一对修正舵,其中减旋舵受空气作用而产生的导转力矩与电磁力矩结合起来共同控制引信的低速旋转及目标姿态。减旋舵的导转力矩的变化趋势如图9所示。
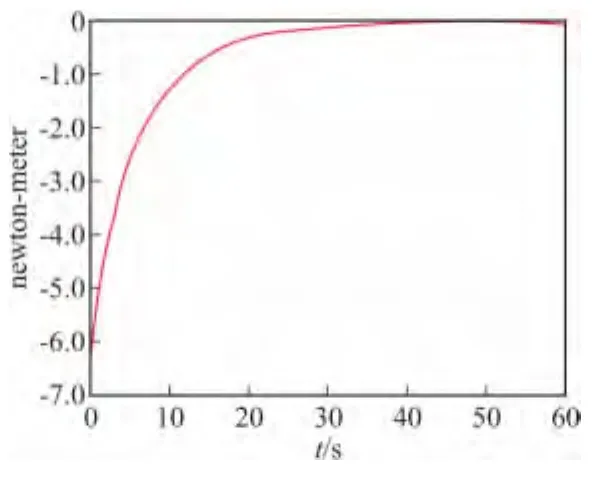
图9 6°舵偏角时减旋舵导转力矩变化
从图9中引信的导转力矩变化趋势可以看出,在弹丸出炮口后10 s的时间内,导转力矩变化率很大,且力矩的值变化也很大。在10 s以后,导转力矩变化率较小,且力矩值的变化也相对较小。
结合上述的导转力矩变化趋势,利用电机对引信姿态进行控制,当电机的电磁力矩取值范围在1.5 N·m内时,设定在出炮口5 s后开始控制引信滚转在目标姿态,则在5~80 s的控制范围之内,引信实际被控制的时间是13~80 s,如图10所示。

图10 电磁力矩在1.5 N·m内时的控制能力
当电机的电磁力矩取值范围在2.0 N·m范围内时,同样设定在炮弹出炮口后5 s时起控,则在5~80 s的控制范围内,引信实际被有效控制的时间是7~80 s,如图11所示。
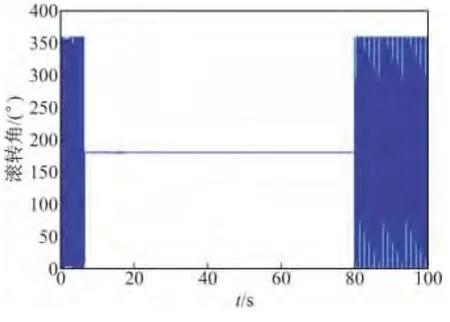
图11 电磁力矩在2 N·m内时的控制能力
综合以上可以得到,电磁力矩的取值直接影响引信姿态的控制时间,电磁力矩越大则对引信的控制能力越强,但对电机的要求会大大提高并会增加成本。
5 修正能力分析
以舵偏角为6°时的修正弹模型为例,已知该炮弹按照射角50°,初速800 m/s发射。在上述条件下的修正弹经过弹道方程解算,得到射程约为22.5 km。当修正舵处于特定位置时,它能为横向修正提供侧向力,而在特定时间内持续性的固定在某一值则能得到此位置下的最大修正能力,在此选取时间t=35 s处作为固定修正舵时间点并进行持续修正,来观察舵偏角分别为2°、4°、6°时弹道修正效果如图12。通过外弹道仿真分析,得到6°舵偏角时的修正量,如表1所示。
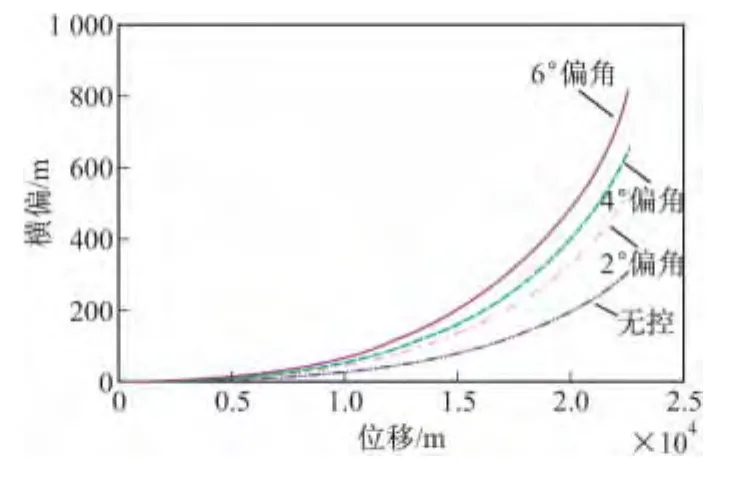
图12 修正弹最大修正能力

表1 弹丸修正能力与舵偏角关系
由结果可以看出,弹丸的修正能力与舵偏角有直接关系,舵偏角越大,弹丸的修正能力越强,但必须满足弹丸的飞行稳定性和电机控制能力。
6 结论
文中重点探讨了如何对固定式鸭舵修正机构舵偏角进行选择,建立了不同舵偏时的气动仿真模型,并得到了各情形下的气动力数据,通过分析可以得出:舵偏角对弹丸翻转力矩及舵翼升力影响较大,且舵翼升力随着舵偏角的增大而增大;对鸭舵导转力矩影响较大,且舵偏角越大则舵面导转力矩越大。
建立了运动学仿真模型,通过对弹丸外弹道飞行状态的模拟,可以看出当舵偏角在6°以下时,弹丸可以全弹道稳定飞行,但当舵偏角达到8°时,弹丸无法稳定飞行。
通过对电机控制能力的分析,可以得出舵翼导转力矩的大小直接影响对电机的合理选择。同时,电机的电磁力矩取值范围也限制了舵偏角的取值。
通过利用适合修正弹的弹道模型对弹丸的修正能力进行仿真,得出了稳定飞行时不同舵偏角下的修正能力。
综合以上得出,若要合理选择舵偏角,须把弹丸的飞行稳定性、修正能力、电机的合理性等综合考虑才能最终合理的选择一种符合修正机构气动布局的舵偏角。
[1]郝永平,孟庆宇,张嘉易.固定翼二维弹道修正弹气动特性分析[J].弹箭与制导学报,2012,32(3):171-177.
[2]刘恒,霍鹏飞.弹道修正引信菱形翼型等腰梯形十字减旋翼[J].探测与控制学报,2009,31(6):47-50.
[3]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:141-143.
[4]徐明友.火箭外弹道学[M].哈尔滨:哈尔滨工业大学出版社,2004:10-15.
[5]张嘉易,王广,郝永平.二维弹道修正弹鸭舵修正机构气动特性研究[J].弹箭与制导学报,2013,33(2):88-91.
[5]雷文星,田晓丽,吴建萍,等.一维弹道修正弹的气动特性与修正量研究[J].弹箭与制导学报,2012,32(6):131-135.
[6]William J Larkin,Mitch Thomas.Atmospheric flight of a variable-bend body[J].Jounal of Guidance and Control,1979,2(5):382-387.
[7]Lock R C.Test cases for numerical methods in two-dimensional transonic flows,AGARD-R-575-70(AD715554)[R].1970.
