基于下视序列图像的无人机测速方法*

黄志仁，陈 楸，何 颖，李岁劳

(西北工业大学自动化学院，西安 710129)

0 引言

近年来，摄影测量和计算机视觉[1]应用于无人机导航[2]的研究越来越多，特别是与惯性导航构成组合导航系统。文献[3]利用无人机上的惯性导航系统、激光测距仪或雷达高度表和摄像机采集的序列图像得到无人机的飞行速度。文献[4]使用KLT(Kanade-Lucas-Tomasi)算法[5]，实现了序列图像中相邻两帧图像间的特征点匹配跟踪。

文中着重研究惯性稳定辅助特征点匹配算法，用于估计无人机的地速，在短时失去GPS信号时，可通过航程推算保持可用的定位精度，以利于后续的基于可视地标的精确定位。

1 惯性稳定辅助特征点匹配算法

文中先利用SURF(speeded up robust features)算子[6]提取特征点，再利用速率陀螺提供的航向和姿态角增量确定特征点在下一帧图像的搜索区域，从而加快特征点匹配速度并减少误匹配。

对于相邻两帧图像k－1和k，空间一点在摄像机坐标系下的关系为:

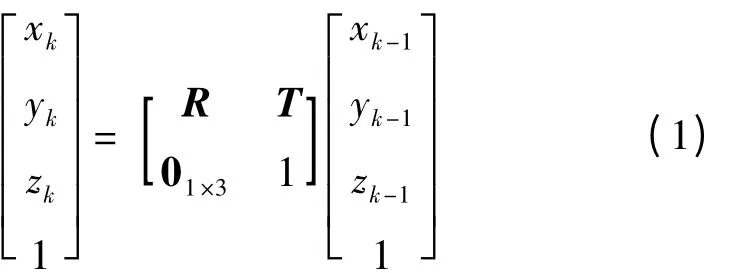
采用“前－右－下”坐标系，旋转变换R可由速率陀螺测量的偏航角增量δψ、俯仰角增量δθ和滚转角增量δφ估计:

平飞时，载机前向位移δx和侧向位移δy是待估计量，由此可确定平移变换:

已知焦距f时，摄像机坐标系中的点可以变换到图像坐标系:

平飞时，可得空间同一点的图像坐标受载机运动的影响:

其中，载机航向和姿态变化产生的影响:

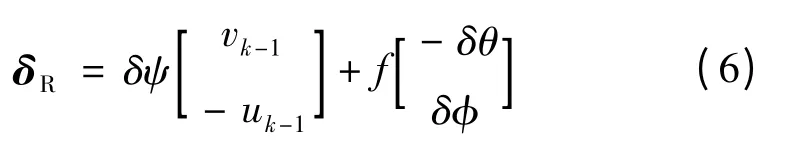
载机平移产生的影响:

由式(5)估计第k－1帧特征点在第k帧中的中心位置(^uk，^vk)，根据传感器的误差特性和载机的相对高度及速度范围估计候选匹配区域的宽度εu和高度 εv，下文仿真实验时取 εu=16 pixel，εv=12 pixel，如图 2(b)所示。

2 仿真实验

本实验采用的序列图像是在基于LabWindows CVI2010和OpenGL开发的虚拟视景仿真平台上模拟拍照获得的。无人机飞行虚拟视景仿真平台的主界面如图1所示。

图1 无人机飞行视景仿真

无人机平均相对高度H=1 057 m，地形起伏约±5 m，飞行速度大小V=29.6 m/s。35 mm相机等效焦距f=70 mm，图像分辨率为640×480时，地面对应拍摄范围为528.5 m×396.4 m。每隔 δt=480 ms拍摄一次，每拍摄一帧图像，无人机飞经14.2 m，则连续两帧图像的重叠率约96%。姿态角误差采用一阶马尔科夫随机过程模拟，时间常数取为3 min。

在Intel core2 E7300 2.66 GHz的CPU和2 G内存的PC机环境下，编程实现文中提出的惯性稳定辅助特征点匹配算法，算法总耗时186 ms，匹配效果如图2所示。匹配特征点用黑色“o”表示，并用数字标号。从图2(a)可以看出完成7对匹配点，无误匹配点。图2(b)是局部放大图，显示第3号特征点在第30帧的匹配结果，其中黑色“+”表示预估特征点(^uk，^vk)，黑色“o”表示得到的匹配特征点，黑色线框表示该特征点的候选匹配区域。图2(c)是SURF算法匹配效果，完成54对匹配点中有9对误匹配点，总耗时为1 732 ms。两种算法比较结果见表1。

图2 匹配结果

表1 匹配算法比较

图3是连续40帧测速结果，速度平均值为30.45 m/s，均方值误差为 1.32 m/s。从仿真实验结果可以看出，仅利用某一帧图像信息测量的瞬时速度绝对误差约2.28 m/s。失去 GPS信号3 min航位推算的北向位置误差约 132.5 m，东向位置误差约76.5 m。

3 误差分析

3.1 载机航向和姿态误差影响

图3 速度检测结果

偏航角误差eψ直接影响测量速度的方向。俯仰角误差eθ直接影响前向位移，滚转角误差 eφ直接影响侧向位移，故两者都影响测量速度的大小。

陀螺漂移可以用加速度计测量的垂线来抑制，可以保持在 3° 以内，故可以设 eθ=eφ=3° ，由 eθ和 eφ带来的速度误差都很小，约0.001 4 m/s。

3.2 速率陀螺测量误差的影响

速率陀螺测量的姿态角增量误差对速度测量误差影响较大，在此只分析俯仰角增量误差eδθ带来的影响，如图4所示。

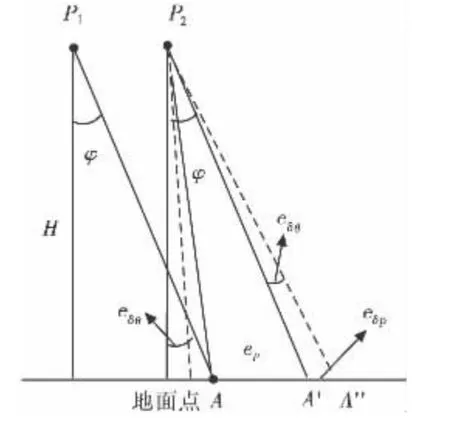
图4 俯仰角增量误差的影响

摄像机光心在两个时刻的位置为P1和P2，对地面点A的投影线与垂线的夹角为φ，由于速率陀螺测量俯仰角增量不准而导致垂线偏离的角度为eδθ。实际位移，由eδθ带来的位移误差为:

所以速度误差为:

若eδθ=0.05°，按上文的仿真条件计算得到该速度误差为1.92 m/s。由速率陀螺和加速度计构成垂直陀螺，姿态误差可以限定在3°以内，由此可以抑制陀螺漂移对定位误差的影响。

3.3 相对高度测量误差和地面起伏的影响

图像匹配得到的像差转换到实际相对地面的偏移量时，需要根据飞行高度来确定对地面的成像分辨率，参考式(7)。如图5所示，根据相似三角形原理，由高度测量误差eδH带来的速度误差:

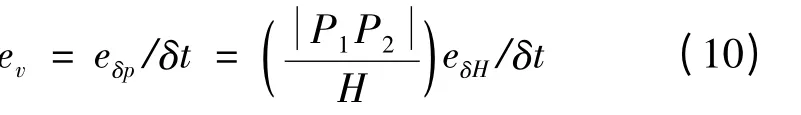
图5 高度测量误差的影响

实际飞行中的高度信息由雷达高度计或激光测距仪等提供，其误差包括随机误差和系统误差。对于随机误差可通过数据平滑进行消除和抑制;但系统误差将直接影响测量精度。若高度存在1%的相对误差，则测速结果也存在1%的相对误差。

4 总结

文中在无人机平飞序列成像的状态下，结合陀螺仪和高度计提供的信息，研究了实时、较高精度测量无人机地速的方法，并进行了仿真实验。利用低成本的MEMS陀螺仪，采用文中提出的方法，就可以得到较高精度的无人机地速，同时可以实现短时间内的较高精度的航位推算和轨迹跟踪。

[1]Kendoul F. Survey of advances in guidance，navigation，and control of unmanned rotorcraft systems[J]. Journal of Field Robotics，2012，29(2):315 －378.

[2]吴显亮，石宗英，钟宜生.无人机视觉导航研究综述[J].系统仿真学报，2010，22(1):62－65.

[3]Wang J L，Garratt M，Lambert A，et al.Integration of GPS/INS/Vision sensors to navigate unmanned aerial vehicle[C]//International Archives of Photogrammetric，Remote Sensing and Spatial Information Sciences，2008:963－969.

[4]Conte G，Doherty P. An integrated UAV navigation system based on aerial image matching[C]//Proceeding of the IEEE Aerospace Conference，2008:1－10.

[5]Shi J，Tomasi C. Good features to track[C]//Computer Vision and Pattern Recognition，IEEE Computer Society Conference on Proceedings CVPR’94，1994:593－600.

[6]Bay H，Tuytelaars T，Van Gool L.Surf:Speeded up robust features[M].Computer Vision-ECCV 2006. Springer Berlin Heidelberg，2006:404 －417.