基于三点支撑的等效轴角调姿法

邓忠林 张哲(沈阳航空航天大学航空航天工程学部(院),辽宁沈阳 110136)

基于三点支撑的等效轴角调姿法

邓忠林 张哲(沈阳航空航天大学航空航天工程学部(院),辽宁沈阳 110136)

为提高飞机大部件装配质量,充分发挥大部件对接并联平台的工作效率,计算验证在小角度下通过等效轴角姿态调整方法,使围绕参考坐标系坐标轴转动三次减少为绕等效轴转动一次的调姿方法依然准确有效,并根据计算定量的给出等效转角与坐标值之间的变化关系,从而简化轨迹规划任务,最后通过螺旋理论举例分析并联调姿机构的自由度,为以后并联结构调姿平台的研究提供理论依据和技术基础。

位姿调整 等效轴转动 轨迹规划 自由度

飞机大部件对接在总装阶段对接过程中要求对接部件姿态和位置快速精确的调整,调姿方法基于三点支撑,通过三个精密三坐标POGO柱互相协调运动,依次完成平动与转动的姿态调整任务[1]。本文在调姿角度较小的情况下引入基于三点支撑的等效转动方法调整对接部件姿态,证明在小角度姿态调整下将原本需要绕三个坐标轴的旋转运动合为绕空间等效轴线的旋转运动的调姿方法是可行的,其运动轨迹映射到对接平台所在坐标系后该运动轨迹在以等效轴为轴线的空间圆弧上;然后定量分析支撑点坐标与等效轴角的变化关系,最后使用螺旋理论举例验证由POGO柱组成的等效并联机构自由度满足要求。

1 姿态转换关系

奇异值分解法能够较准确地计算两个点集之间的位姿转换关系[2]。其核心思想是计算是在两个点集拟合后偏差最小的情况下,通过两个点集的质心求出转化关系,这个转化关系就是对接部件姿态调整所需要的旋转矩阵R与平动矢量T。

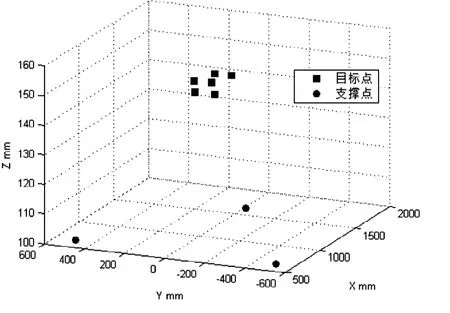
图1 支撑点与{ Pt}Fig 1 Supported Points and { Pt }

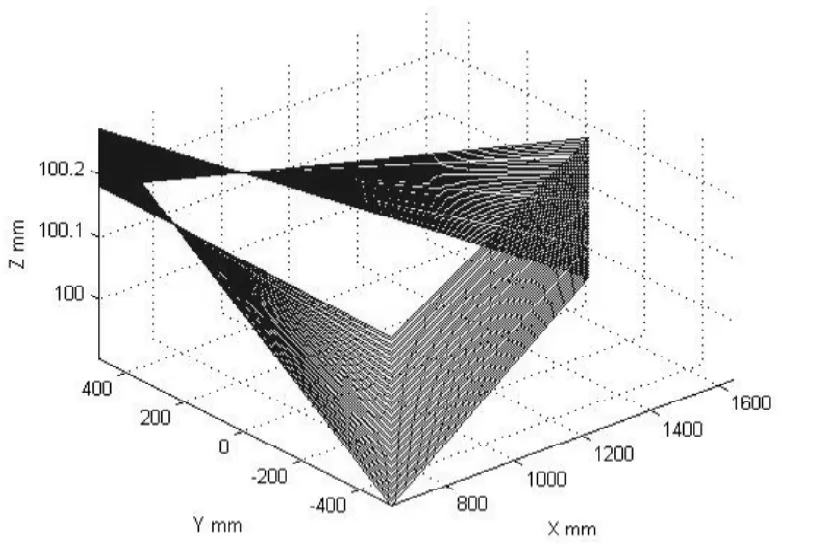
图2 轨迹Fig 2 Trajectory

以上算法在 det(R)＝1时成立,这里旋转矩阵R与平动向量T为部件对接过程中姿态调整的转换关系。

本文讨论的等效轴角坐标系表示法是在空间中找到一个通过原点的一般转轴,围绕该转轴转动角度 θ使对接点集与目标点集重合后误差最小,该轴线的单位向量由旋转矩阵R反解出来,为了简化问题,需要使目标点集与对接点集坐标系的原点重合,实际操作中通过该一般轴旋转后使对接部件直接入位,由此会产生碰撞损坏部件,所以计算时先将对接点集在对接方向上平移矢量-1

RT,即先平移使两点集中心重合,等效轴通过参考坐标系原点,然后进行旋转;但是实际对接过程中则是先旋转,再平移入位。

设矢量K为有限旋转的等效轴,则对接点集相对于目标点集的一般姿态可用等效旋转矩阵表示,当选择目标点集坐标系的主轴作为旋转轴时,等效旋转矩阵变为平面旋转矩阵。从一个给定的旋转矩阵反求出单位向量K和旋转量θ,公式(7)(8)总能计算出一个0°在到180°之间的值[6]。通过计算当

图3 坐标值与 θ变化关系Fig 3 Coordinate Values and θ

表1 两种解算方法误差比较Table 1 Comparison of Two Methods Error

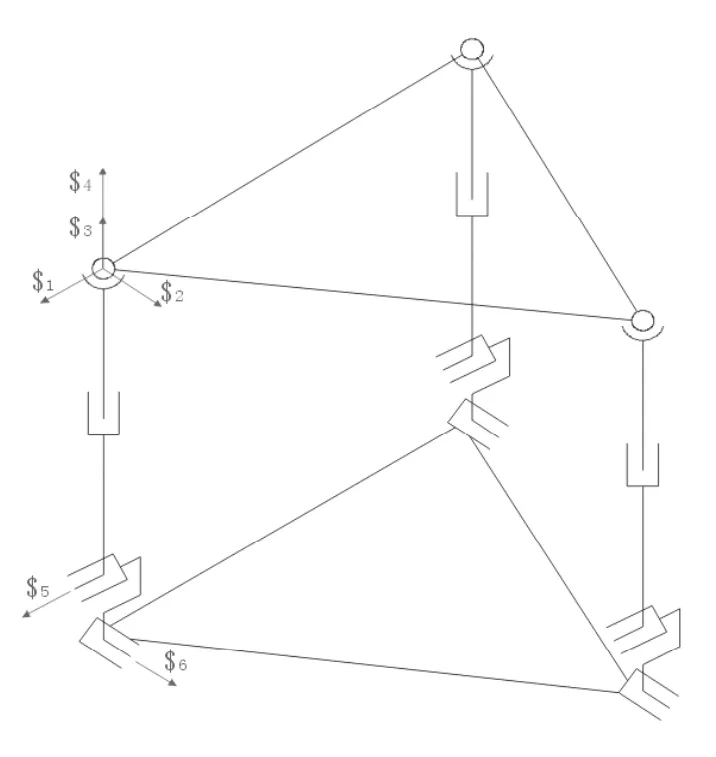
图 4调姿原理Fig 4 Theory of the Posture Alignment

由其矩阵误差的二范数判断,在小角度情况下等效轴角坐标系法依然适用,可以找到稳定的等效轴、角。

2 计算验证

等效轴角 (K,θ)将绕坐标轴多次旋转的问题转化为绕空间一条直线旋转的问题,则点集到点集的理论轨迹为以单位向量K所表示的空间直线为旋转轴旋转 θ角的N段圆弧,N表示点集中点的总数,由于各点到单位向量K的距离不同,所以其表示的圆弧轨迹半径不同。点到单位向量K的直线距离由式(9)给出:

下面分别用高斯-勒让德求积公式、迭代法验证式(14):

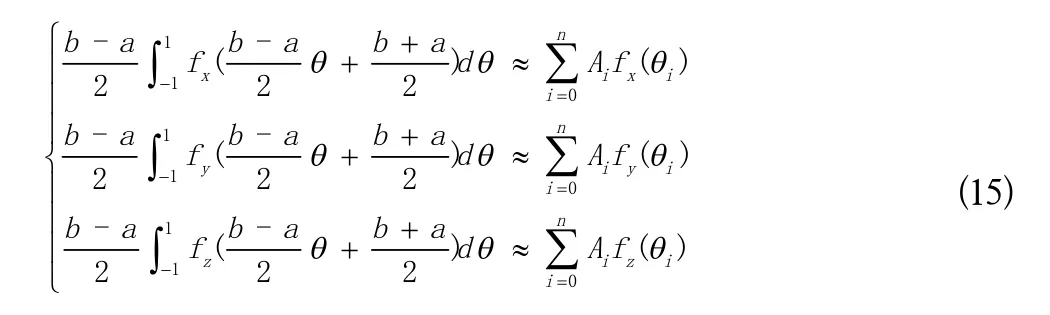
式(15)所得结果与点集{Pd} 比较,所得差值的二范数为0．11362,传统SVD法所得结果与点集{Pd}比较,所得差值的二范数为0．11362,因此判断可以使用式(14)表示坐标点 (x,y,z)与 θ的关系。

由于坐标的步长值在精密导轨可实现的精度范围3μm附近,平均每3个步长就会造成可观测的误差积累,且调姿过程中各支撑点之间联动误差会在对接部件及其保型架内产生内应力,所以实际应用时需要权衡转角控制精度的选取以符合执行机构要求。

3 自由度分析

以上计算要求并联机构实现三个平动三个转动共6个自由度,下面以POGO柱和飞机大部件保型架组成的等效并联机构为例,分析该等效并联机构自由度是否满足要求。

POGO柱、动平台(对接大部件保型架)和静平台(台架)组成等效并联机构如图4所示。该机构有三个分支,每个分支的起点是位于静平台上的移动副,向上联接相垂直的移动副,这两个运动副使POGO柱2D平动,再向上为沿着Z轴的移动副,最后与球副相联。取其中一个分支建立坐标系,原点设为静平台上移动副初始值,Z轴通过球副中心向上,则该分支的运动螺旋如下:

前三个表示球副,后三个表示移动副。由式(16)组成的系数矩阵的秩为6,所以判断没有公共的反螺旋,无局部自由度,无公共约束,使用修正的G-K公式计算该机构的自由度如下:

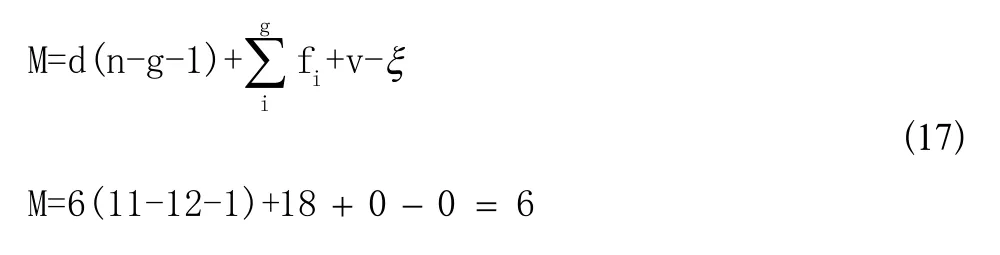
因此,POGO柱与保型架组成的等效并联机构可以实现三个平动和三个转动共6个自由度。进一步检查机构自由度的全周性,发生微小位移后自由度保持不变,所以该机构自由度具有全周性。

如果将球副替换为U型副,那么取其中一个分支建立坐标系,其运动螺旋如下:

由式(18)组成的系数矩阵的秩为5,该分支唯一反螺旋限制该分支顶点沿空间一固定矢量平动,三条分支不相交的三个反螺旋共同作用,等效于限制动平台空间转动,没有线性相关的反螺旋作用在动平台,所以判断无公共约束,无局部自由度 ξ,则通过修正的G-K公式计算该机构的自由度为3,只有空间平动的能力,不能满足对接平台6个自由度要求。

POGO柱、动平台(对接大部件保型架)和静平台(台架)组成的等效并联机构还需考虑超确定输入问题,三个分支共需要9个输入驱动,而空间调姿只有6个自由度,所以在组合时应选取其中6个为主要输入,3个为配合输入满足一定的位型关系,例如满足式(13);或者分阶段首先选取3个Z向移动作为主要输入,6个为配合输入满足一定的位型关系,然后选取X、Y向移动作为整体输入,以此来处理超确定输入问题。

4 结语

传统的大部件对接过程姿态调整部分任务需要多步,并没有完全发挥并联平台的效用。本文引入等效轴角坐标系表示法为支撑点的轨迹规划提供理论依据,同时验证在小角度状态下该方法依然有效,且解算时间在接受范围内。求得支撑点坐标与旋转角之间的变化关系后,通过在实际精度条件下离散旋转角得到该点坐标与等效角变化关系,并证明该离散方法与传统方法理论上效用一致且路径更短更平滑,最后举例验证等效并联机构能否满足部件对接时的自由度要求,并说明POGO柱作为分支模块并不是简单叠加,需要考虑随之带来的超确定输入问题。

本文讨论在小角度下姿态调整问题,在成熟可靠的技术条件下可将平移距离缩短,使部件围绕空间中一般单位向量旋转,相对于围绕经过参考坐标系中心的单位向量旋转增加了旋转半径,使其轨迹更平滑,有效减少各支撑点联动造成的误差。该方法为飞机部件对接并联平台提供一定的理论依据,但没有引入实际执行机构的误差模型,是否真正能够应用于对接平台有待实验验证。

[1]郭志敏,蒋君侠,柯映林.基于POGO柱三点支撑的飞机大部件调姿方法[J].航空学报,2009,30(7):1319-1324.Guo Zh M, Jiang Junxia, Ke Yinglin.Posture Alignment for Large Aircraft Parts Based on Three POGO Sticks Distributed Support[J].Acta Aeronautica et AstronauticaSinica, 2009, 30(7):1319-1324.

[2]Arun K S,T S Huang,S D Blostein. Least-Squares Fitting of Two 3-D Point Sets[J].Transactions on Pattern Analysis and Machine Intelligence, IEEE,1987,9(5):698-700.

[3]邱宝贵,蒋君侠,毕运波,等.大型飞机机身调姿与对接试验系统[J].航空学报,2011,32(5):908-919.

Qiu Baoguo,Jiang Junxia, Bi Yunbo, et al.Posture Alignment and Joining Test System for Large Aircraft Fuselages[J].Acta Aeronautica et AstronauticaSinica, 2011,32(5):908-919.

[4]许国康.大型飞机自动化装配技术[J].航空学报,2008,29(3):734-740.Xu Guokang. Automatic Assembly Technology for Large Aircraft[J].Acta Aeronautica et AstronauticaSinica,2008,29(3):734-740.

[5]王少锋,张进华,刘志刚 等.大型飞机机身壁板装配位姿调整系统的运动规划[J].西安交通大学学报,2011,45(3):102-106.Wang Shaofeng,Zhang Jinhua,Liu Zhigang,et al.Motion Planning for Posture Alignment Machine Tool Oriented Fuselage Panel[J].Journal of Xi’an Jiaotong University,2011,45(3):102-106.

[6]John J.Craig. Introduction to Robotics: Mechanics and Control[M].Prentice Hall,3 edition,2006:44-51.

[7]黄真,刘婧芳,李艳文.论机构自由度:寻找了150年的自由度通用公式[M].北京:科学出版社,2011.08.